基于正交设计的滞洪区路堤边坡敏感性研究
2022-02-25朱晓东肖云飞薛丹璇
朱晓东,肖云飞,薛丹璇
(中国市政工程华北设计研究总院有限公司,天津市 300074)
0 引 言
随着国家与各地区对高速公路网的组织规划日益清晰,越来越多修筑于滞洪区中的濒河高速公路被立项,濒河高速公路工程初具规模[1]。因此,有必要深化研究洪水演进时路堤边坡稳定性的变化规律。
滞洪区路堤边坡稳定性的影响因素除了路堤边坡本身的坡度等几何尺寸以及黏聚力、内摩擦角、渗透系数、重度等物理力学性质[2]外,还要考虑洪水期路堤外水位变化因素对其稳定性的影响[3]。国内外学者对路堤边坡稳定性影响因素进行了相关研究并取得了一些成果。Thorel[4]用离心模型试验方法研究了砂黏土混合料路堤模型的浸水变形性质;张俊荣[5]等采用岩土计算软件Geo-studio分别对砂性土和黏性土填土路基两侧水位变化时的稳定性因素进行研究;李勇[6]采用通用有限元程序ADINA计算分析水位变化对浸水路堤稳定性的影响;吴科亮,丁春林[7]采用有限差分程序FLAC3D基于控制变量法和正交试验法分析了重度、弹性模量、泊松比、粘聚力、内摩擦角等五种物理力学指标对边坡稳定性影响的敏感程度;郝忠[8]等定量化研究库水位骤降下不同非饱和参数对边坡稳定性的影响,并根据正交实验分析法进行了敏感性分析。
综上,已有的研究对滞洪区高速公路路堤边坡稳定性影响因素的研究较少。本文在前人研究的基础上,以天津市某滞洪区范围内高速公路路堤边坡为例,利用MidasGTS有限元软件模拟计算路堤边坡稳定性,并采用正交设计试验方法分析比较洪水位降幅、水位降速和路堤填土渗透系数等因素对路堤稳定性影响的敏感性。
1 滞洪区路堤边坡有限元模型
1.1 有限元模型建立及网格划分
通过对滞洪区路堤断面的调查和统计,采用路堤断面尺寸为路肩宽度6.5m,路缘带宽度2.5m,行车道宽度22.5m,中央分隔带宽度3.0m,路堤高度8m,边坡坡比1∶1.75,两侧坡脚设置混凝土防护,同时在两侧坡面采用桁架单元模拟格栅对坡面的防护(见图1)。

图1 滞洪区路堤边坡有限元模型
土体采用Mohr-Coulomb本构,防护材料采用弹性本构。模型使用平面应变单元进行模拟,网格划分以四边形为主的单元。行车荷载竖直作用在行车道上,设置大小为20kPa。
在数值模拟计算时采用MADIS内置强度折减法,分析控制中的收敛条件设置为位移标准0.001m。模型共计38080个单元,38664个节点。分析控制中考虑初始应力状态和非饱和因素。
1.2 计算参数选取
在数值模拟中由上到下考虑5类岩土材料:①改良石灰土(厚0.6m)、②粉土(厚6m)、③素填土(厚2m)、④粉质黏土(厚15m)和⑤粉土夹粉砂(厚3m)。依据室内试验成果和相关资料确定各土层物理力学参数取值见表1。
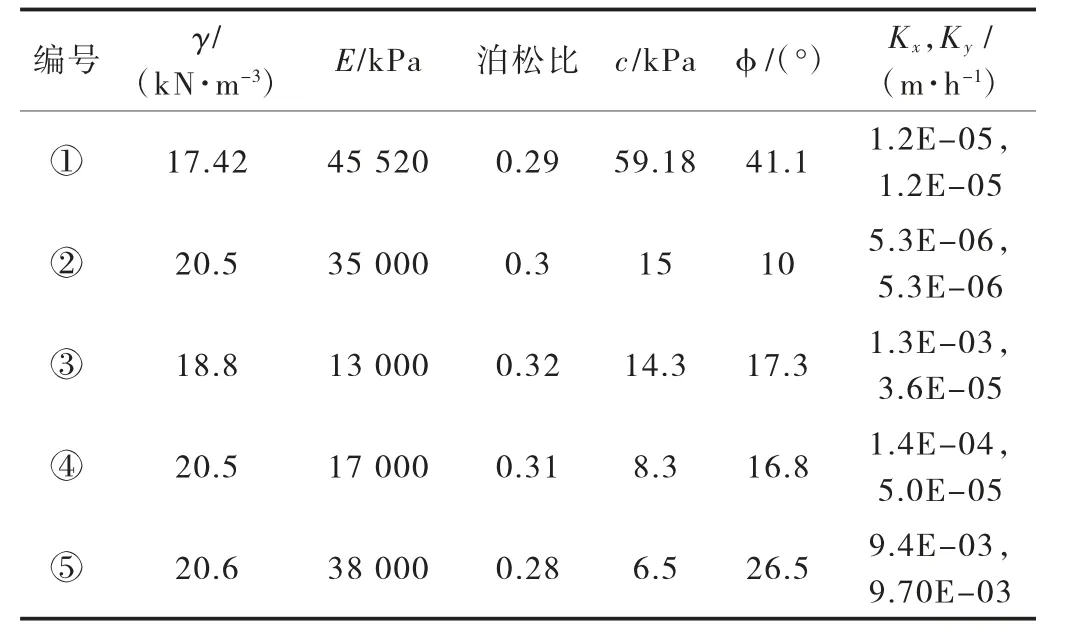
表1 路堤边坡土体参数表
滞洪区路堤边坡防护材料中坡脚混凝土和格栅的弹性模量分别取3.0×107Pa和1.825×106Pa,泊松比分别取0.3和0.2,容重分别取24kN/m3和4.0×10-3kN/m3。
1.3 水位情况选取
滞洪区最大的特点,是在洪水期间路堤边坡两侧水位会在短时间内有较大的变化从而诱发路堤边坡失稳。项目所在地区的滞洪区路堤边坡水位变化情况可以分为以下几种:
情况1:路堤两侧洪水位上升;情况2:路堤单侧洪水位上升;情况3:路堤两侧洪水位下降;情况4:路堤单侧洪水位下降。
2 不同水位情况下路堤稳定性分析
2.1 洪水水位上升过程中路堤边坡稳定性
2.1.1 路堤两侧洪水位上升
首先通过有限元软件内置的强度折减法计算了初始地下水位是位于地面线时路堤边坡的稳定性。图2为此时路堤边坡的塑性云图。计算此时路堤边坡的稳定性系数为1.61。

图2 水位位于地面线时路堤边坡塑性云图
图3 为路堤边坡稳定性系数随洪水位高度变化趋势图,从中可以发现路堤边坡稳定性系数随着两侧洪水位的上升而增大。这是由于在洪水水位上升的过程中,一方面路堤边坡内部填土含水量不断上升,填土的自重增大,同时抗剪强度逐渐降低;另一方面,在水位上升过程中,水对路堤土产生向上的托浮作用。这两种效应共同对路堤边坡稳定性到作用,在路堤两侧洪水水位升高过程中,后者起主导作用。

图3 两侧水位上升时路堤边坡稳定性
2.1.2 路堤单侧洪水位上升
当滞洪区路堤边坡水位单侧变化时,低水位一侧的路堤边坡将处于不利状态。如图4所示,当地下水位在地面线以下0m时,路堤边坡稳定性系数则为1.61。当路堤单侧上升到地面线以上5m时,路堤边坡稳定性系数为1.56。这意味着,在路堤边坡地下水位固定的情况下,抬高改变另一侧的水位,路堤边坡安全系数从1.61降低到1.56,稳定性系数整体呈下降趋势,下降速度先快后慢。

图4 单侧水位上升时路堤边坡稳定性
2.2 洪水水位下降过程中路堤边坡稳定性
2.2.1 路堤两侧洪水位下降
在研究两侧水位同时下降对路堤边坡的稳定性系数变化的影响时,重点分析了水位下降速度和水位下降程度对路堤边坡稳定性的影响。因此选取两种水位下降模式,五种水位下降具体工况,具体如下:(1)降速模式:在这种模式中,假设水位下降均为5m,下降用时分别为:工况一12h、工况二24h和工况三36h;(2)降幅模式:假设水位下降的总用时均为36h,水位下降幅度分别为工况三5m,工况四3m和工况五1m。
图5和图6展示了不同模式控制水位下降过程中,路堤边坡稳定性系数变化情况。首先,由图5可以看出,在降速模式中,路堤边坡稳定性系数先是快速降低,然后缓慢下降,且水位降速越快,稳定性越低。水位下降速度最快的工况一为三种工况中的最危险工况,稳定性系数为1.21。

图5 降速模式

图6 降幅模式
图6 展示了降幅控制水位下降过程中,路堤边坡稳定系数变化情况。通过对比三种工况下路堤边坡稳定性系数变化,发现随着水位下降幅度的减小,路堤边坡稳定性系数降低的趋势逐渐变缓,且降幅越小稳定性系数越大。
2.2.2 路堤单侧洪水位下降
在模拟路堤单侧洪水位下降计算过程中,固定路堤左侧水位高度为地面线上5m,路堤右侧水位按照图5中工况一的方式在12h内骤然降低到地面线即0m,计算这一过程中48h内路堤边坡稳定性系数变化情况,计算结果见图7。

图7 单侧水位下降时路堤边坡稳定性
由图7可以看出,在单侧水位下降的过程中,路堤边坡的稳定性系数先是快速下降,在约12h达到最低点,之后稍有抬升,然后保持平稳。在水位下降过程中最小边坡稳定性系数从2.42降低到最小值1.19,降低了50.8%。
3 影响因素敏感性分析
3.1 正交试验设计
在前文的分析中,分别研究了滞洪区路堤边坡两侧、单侧水位升降等工况下稳定性系数的变化情况。由前文计算和分析研究可知,相比于两侧水位下降的工况,滞洪区路堤边坡两侧原有较高水位,单侧水位在短时间内降低时路堤边坡稳定性最低,为最危险的工况。
因此,下文将研究多因素影响下单侧水位下降时滞洪区路堤边坡稳定性,主要因素包括水位降幅、水位降速和填土渗透系数,每种因素取5个水平,如果采用全面试验法,需要设置不同条件,进行多达125次虚拟仿真试验,存在工作量大和耗时过久的问题。因此本文采用正交试验设计法,对滞洪区路堤边坡特征因素进行组合,通过计算得到各影响因素对最终结果的贡献率。
选择正交试验设计表见表2,其中Tq为某因素在q水平时相应计算结果平均值。

表2 路堤稳定性影响因素水平表
3.2 影响因素敏感性计算和分析
各影响因素对路堤稳定性的影响大小可以通过贡献率来表示。贡献率通过式(4)进行计算,计算结果见表3。

表3 路堤稳定性影响因素贡献表
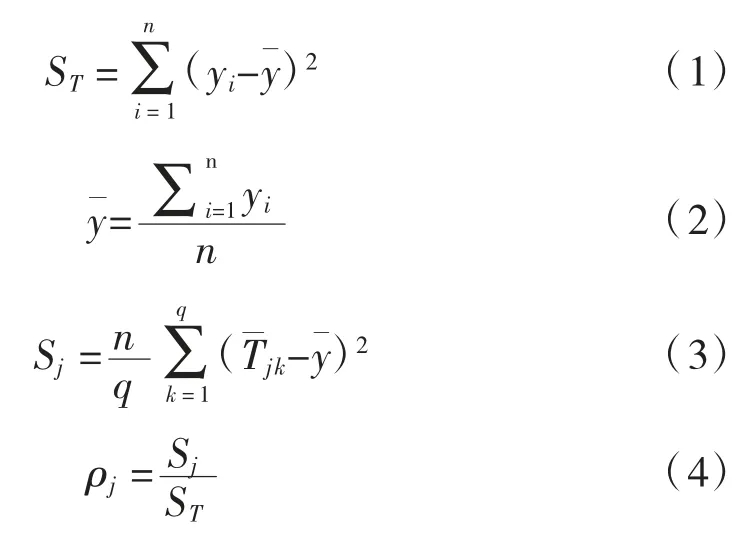
式中:ST表示试验结果波动的总平方和;n是试验次数,本试验中n=25;yi为各次试验结果,i=1,2,3…;y为试验结果的总平均值,本正交试验中y=1.45;Sj为第j列(即第j个因子)的平方和,它表示由于j因子的不同水平引起的试验结果的波动。
通过以上研究表明,在影响路堤边坡稳定性的因素中,影响最大的是水位降幅,贡献率达到88.54%,其次是渗透系数,贡献率为9.07%,再次是水位降速,贡献率为2.39%。这一结果表明在洪水期内,应重点关注滞洪区路堤边坡水位下降幅度,采取各种措施对其进行监测和控制。
4 结论
(1)两侧水位同时升高时路堤边坡的稳定性明显升高,单侧升高时对侧边坡稳定性降低。
(2)洪水水位从较高位置开始下降时,两种情况下的路堤边坡的稳定性均逐渐减小,且降速越快、降幅越大时的稳定性越低。此外,相同条件下单侧水位下降时的稳定性更低。
(3)通过比较水位降幅、水位降速和渗透系数三个因素的敏感性可知:水位降幅对路堤边坡的影响最大。
