考虑滑移效应的页岩基质纳米孔隙中压裂液滤失速度分形计算新模型

纪国法，丁江,张琦,王可可,高仪君,刘炜

1.非常规油气省部共建协同创新中心(长江大学)，湖北 武汉 430100

2.长江大学石油工程学院，湖北 武汉 430100

3.中国石油吐哈油田分公司勘探开发研究院，新疆 哈密 839009

4.成都理工大学能源学院，四川 成都 610059

5.中国石油川庆钻探工程公司地质勘探开发研究院，四川 成都 610051

6.中国石化江汉油田分公司石油工程技术研究院，湖北 武汉 430035

水平井分段压裂技术是页岩气商业开发的关键，其原理就是利用大规模滑溜水实现体积改造，形成复杂缝网。从国内外现场返排统计数据来看，页岩气井压后返排率普遍偏低[1-4]，大量滑溜水被滞留在页岩基质的纳米孔隙中，减缓气体的解吸、扩散和渗流过程[5-7]，进而影响页岩气井压后产量的长期稳定性[8]，表现为压后产量递减快的特点。

一般认为，微米级微通道内的流动符合泊肃叶(Hagen-Poiseuille)流动规律[9]。然而，页岩基质同时发育大量占主导地位的纳米级孔隙[10，11]，在纳米空间内液体流动属于受限流动，不可直接采用Hagen-Poiseuille流动理论描述。程友良等[12]采用Comsol模拟微通道中水的Hagen-Poiseuille流动，认为较低流速下滑移长度对流量的影响较为显著。目前认为，自然界中的真实多孔介质在一定尺度范围内具有分形特征[13-16]。YANG等[17]通过对四川盆地下寒武统页岩样品结构的研究，指出页岩复杂的孔隙结构具有分形特征。蔺景龙等[18]、张思勤[19]基于分形理论将储层的渗透率与孔隙度、迂曲度和孔隙半径联系起来，得到了储层岩石渗透率的预测模型。JI等[20]运用分形理论建立了考虑3种受控机理的压裂液滤失系数计算新模型。分形理论的应用具有一定的借鉴意义。

笔者考虑滑溜水在受限的纳米孔隙空间内流动的滑移特殊性和毛细管压力效应，借用分形理论描述了页岩基质的纳米孔隙的复杂性，建立反映纳米孔隙中的压裂液滤失速度新模型，对揭示滑溜水在页岩基质中滤失行为规律具有指导意义，旨在为页岩气压后返排与焖井制度及优化提供理论参考。

1 压裂液滤失速度新模型

图1 页岩基质压裂液滤失单毛细管示意图 Fig.1 Schematic diagram of single capillary filtration of shale matrix fracturing fluid

由于页岩基质具有纳米级孔隙[10，11]、超低含水饱和度[21]、亲水/亲油双亲性[22]的特点，其压裂过程中大量滑溜水压裂液会受驱替压力和毛细管压力的双重作用，加速滤失进入基质中(见图1)。受限流体往往表现为较强的滑移效应，通过试验或分子动力学模拟中测得该效应下的滑移长度一般为几个nm到μm的量级[23，24]。

假设在半径为r的单毛细管流动过程中，存在水相和气相2种流体，液相为润湿相，毛细管压力为pc，流动状态为层流。根据毛细管流速公式可得界面两侧2个单相流体流动速度表达式：

(1)

在该驱替流动过程中，毛细管压力为驱替动力，表达式如下：

(2)

由于流体连续流动，r不变，则v1=v2，且等于两相界面的移动速度，则有：

(3)

对式(3)分离变量并积分，整理可得：

(4)

对式(4)求导得到流体流动速度表达式:

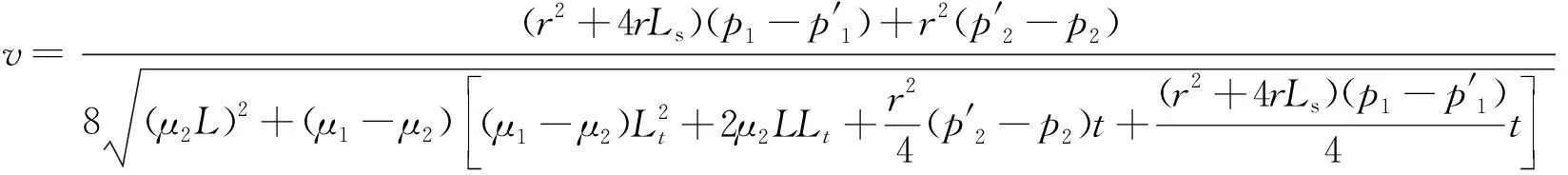
(5)

式中：pc为毛细管压力，Pa；Lt为在t时刻气-水界面到入口端的实际距离，m。

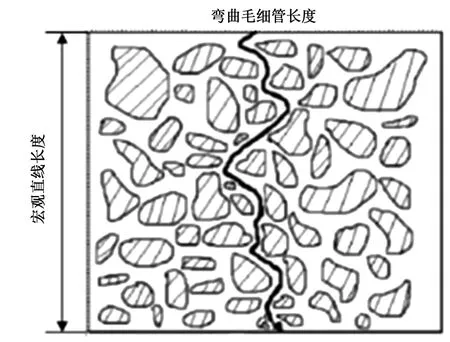
图2 多孔介质中的弯曲流线示意图 Fig.2 Schematic diagram of bending streamlines in porous media

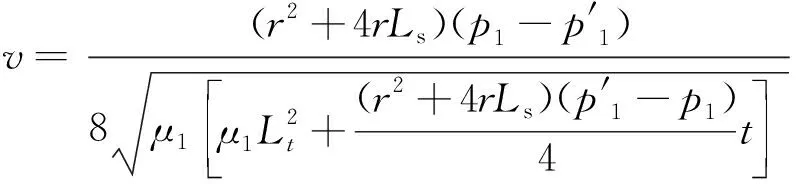
(6)

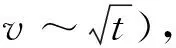
如图2所示，多孔介质中流体流动通道一般都是弯曲形态，流通路径Lt亦为弯曲毛细管长度，其数值大于流体流动的宏观直线长度L0。由于页岩基质孔隙结构具有分形特征[8,14-17]，其压裂液实际流经路径可由式(7)表示[25-29]:

(7)

其中：

(8)

式中：d为页岩基质孔隙直径(d=2r)，m；Nt为迂曲度分形维数(计算时采用迭代法确定)，1；L0为沿宏观压力梯度方向上的直线长度或特征长度，m；Np为页岩基质孔隙结构分形维数，1；dmax为页岩基质最大孔隙直径，m；dmin为页岩基质最小孔隙直径，m；φ为页岩基质孔隙度，1；NE为欧氏空间维数，取值1、2、3;τ为页岩孔隙迂曲度，1。

采用压汞法测试页岩基质毛细管压力曲线，可获取其孔径分布规律[30]；针对不同的滑溜水压裂液体系，可采用试验手段测试其润湿角、表面张力[31]，然后可计算出毛细管压力大小。最终可联立式(8)、式(7)、式(6)、式(2)分析不同参数对滤失速度的影响。

2 影响因素分析

结合页岩基质超低孔、超低渗特点，以表1中所示参数为基本输入参数，进行算例计算与分析，研究滑移长度、压裂液黏度、基质纳米孔隙半径、毛细管压力等4个因素对滤失速度的影响。

表1 算例基础参数

2.1 滑移长度

分别取滑移长度Ls=0、100、500、1000nm，其中Ls=0nm表示无滑移效应，计算结果见图3。从图3中曲线变化趋势可知：①随着滤失时间的增加，滑溜水滤失速度降低，最后趋于稳定；②考虑滑移长度时，1～500s内滤失速度降低幅度最大；无滑移效应时，1～100s内滤失速度降低幅度最大；③考虑基质纳米孔隙中压裂液的滑移效应后，滤失速度大幅度增加，滑移长度越大，滤失速度越大，说明在纳米受限空间内的压裂液滤失过程，滑移效应不容忽视。

2.2 压裂液黏度

分别取滑溜水压裂液黏度为5、10、20、30mPa·s，计算结果见图4。从图4中曲线变化趋势可知：①随着滤失时间的增加，滑溜水滤失速度降低，最后趋于稳定，在1～500s内滤失速度降低幅度最大；②不同滑溜水压裂液黏度下滤失速度不同，黏度越大，流体流动阻力亦越大，相同驱替压差下，滤失速度就越小。

图3 滑移长度对滤失速度的影响Fig.3 Effect of slip length on filtration rate图4 压裂液黏度对滤失速度的影响Fig.4 Effect of the viscosity of fracturing fluid on filtration rate

2.3 基质纳米孔隙半径

分别取孔隙半径为1、20、200、500nm，计算结果见图5。从图5中曲线变化趋势可知：①随着滤失时间的增加，滑溜水滤失速度降低，最后趋于稳定；②不同孔隙半径下滤失速度不同，孔隙半径越大，流体流动阻力越小，相同驱替压差下，滤失速度就越大；③孔隙半径为20、200、500nm时，1～500s内滤失速度降低幅度最大，孔隙半径为1nm时，1～50s内滤失速度降低幅度最大，说明基质纳米孔隙半径越小，滤失速度越小，其降低幅度也越快。

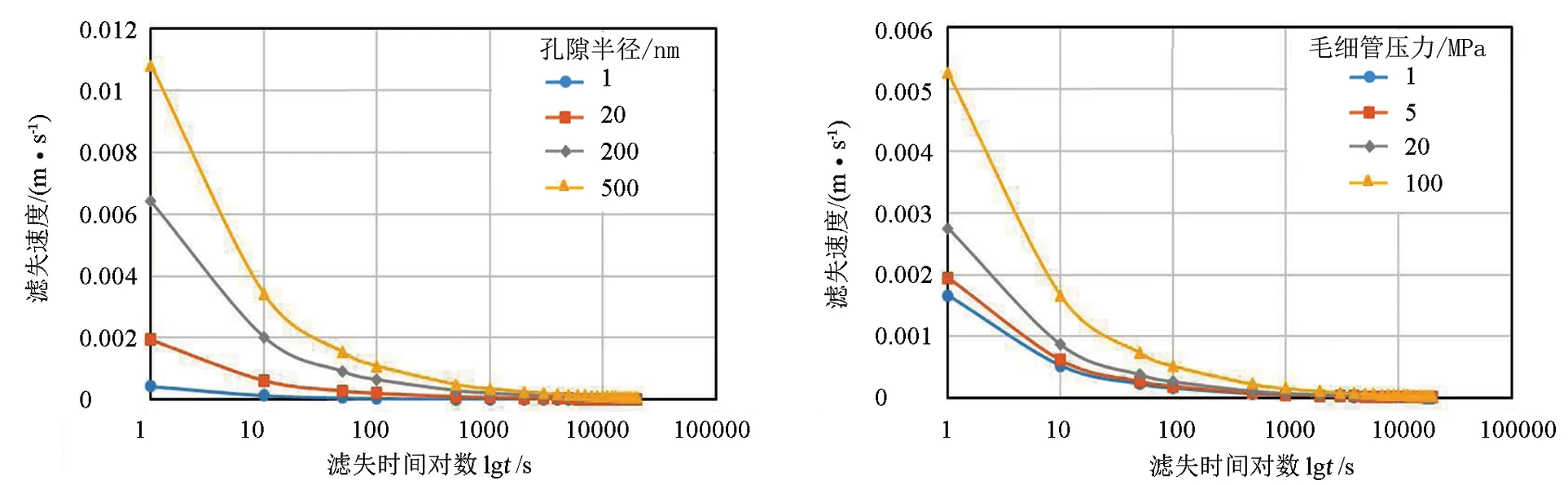
图5 基质纳米孔隙半径对滤失速度的影响Fig.5 Effect of matrix nano-pore radius on filtration rate图6 毛细管压力对滤失速度的影响Fig.6 Effect of capillary pressure on filtration rate

2.4 毛细管压力

分别取毛细管压力为1、5、20、100MPa，计算结果见图6。从图6中曲线变化趋势可知：①随着滤失时间的增加，滑溜水滤失速度降低，最后趋于稳定；②不同毛细管压力下滤失速度不同，毛细管压力越大，驱替压差越大，滤失速度就越大；③毛细管压力为1、5、20MPa时，1～500s内滤失速度降低幅度最大，毛细管压力为100MPa时，1～1000s内滤失速度降低幅度最大，说明毛细管压力越大，滤失速度越大，其降低幅度也越慢。

3 结论

针对页岩基质复杂纳米孔隙结构的分形特征和受限性，开展了机理研究，得到如下结论：

2)以页岩基质超低孔、超低渗特点为基础，结合现场使用压裂液性质，讨论了滑移长度、压裂液黏度、纳米孔隙半径、毛细管压力等4个因素影响下的滤失速度变化趋势：①滑溜水滤失速度随滤失时间增加而降低，最后趋于稳定；②基质纳米孔隙中压裂液滑移效应不容忽视，滑移长度越大，滤失速度越大；③滑溜水压裂液黏度越大，流体流动阻力亦越大，滤失速度就越小；④基质纳米孔隙半径越小，滤失速度越小，其降低幅度也越快；⑤毛细管压力越大，滤失速度越大，其降低幅度也越慢。研究结论可为页岩气压后返排与焖井制度及优化提供理论参考。