剪切载荷作用下岩体结构面动态接触特征数值模拟
2022-02-25蒋宇静张孙豪栾恒杰王长盛
蒋宇静,张孙豪,栾恒杰,王长盛,王 冬,韩 伟
(1. 山东科技大学 能源与矿业工程学院,山东 青岛 266590;2. 山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地,山东 青岛 266590;3. 长崎大学 工学研究科,日本 长崎 852-8521)
矿山、隧道、边坡以及水利水电等各类工程岩体中存在大量的各种结构面,如断层、节理、层理和裂隙等,破坏了岩体的整体性,导致岩体的强度和稳定性显著降低。众多工程实践表明:结构面的剪切变形和滑移会导致工程失稳问题,严重威胁着人们的生命和财产安全。例如,当受到地下采矿和建筑活动干扰时,断层容易发生滑动,从而对井下采掘空间甚至矿井地表造成严重损害,采矿诱发的断层滑动引起的破坏性地震或岩爆正在成为世界范围内深部开采安全的主要威胁。因此,深入研究岩体结构面的剪切特性对于工程灾害防控具有重要意义。
自19世纪60年代以来,已有颇多关于岩体结构面剪切特性的研究成果,主要包括剪切强度、表面破坏特征、结构面抗剪强度与结构面表面形貌之间的关系以及岩石类型、边界条件和加载方式等因素对它们的影响规律。岩体结构面剪切特性与表面形貌之间的关系更是岩石力学界在过去几十年中研究的热点问题。诸多学者提出了不同的JRC表征方法来描述结构面的表面形貌,并建立其与结构面剪切特性的关系。但是,这些JRC表征方法多是静态的,无法表达剪切过程中粗糙体的部分退化、互锁和分离,这限制了静态JRC表征方法的功效。实际上,岩体结构面的剪切特性与接触面的分布密切相关,各类因素大都是通过影响结构面的表面接触特征进而影响其剪切特性。在剪切过程中,结构面只有部分是接触的,并且接触部分也随着表面的滑动和破坏不断变化。从力学的观点来看,结构面的JRC必须以此为基础来表征,了解接触区域在法向和剪切载荷下的行为是量化结构面“有效”JRC的关键。因此,剪切作用下岩体结构面三维表面动态接触特征的研究对于结构面剪切行为的评价和预测是至关重要的。
鉴于以上认识,国内外学者采用理论分析、室内试验和数值模拟等方法对岩体结构面三维表面接触特征进行了研究。理论研究方面,ZHAO等在Barton准则的基础上考虑了结构面接触对节理抗剪强度的影响,引入了节理匹配系数对Barton 准则进行修正。GRASSELLI首先研究了结构面接触面积比与表面形貌参数的关系,并将接触面积比作为一个重要指标,建立了结构面表面形貌参数与剪力学特性关系。该方法受到广泛的认可,许多学者在此基础上继续研究了接触面积比对粗糙节理剪切特性的影响,并发展了诸多新的结构面剪切强度模型。但是,目前理论研究中对于剪切过程中结构面表面接触特征的演化鲜有报道。
试验研究方面,PARK等总结指出:一些学者通过在结构面处插入压敏纸、可变形薄膜、低熔点金属和环氧树脂等材料获取结构面的接触特征,但插入材料会影响结构面的剪切特性,且当考虑剪切位移时,更难以得到合理的结果;也有一些学者通过分析热电偶温度分布、电流通过阻力和CT扫描来间接确定结构面的接触特征,但解释测量信号和将测量信号定量应用于实际接触区域时引入了可能的误差,以上试验方法仍需完善。近年来,透明材料在岩石力学领域得到广泛应用。JU等利用3D打印技术和对应力敏感的光聚合物制作了透明的粗糙断层模型,并提出了一种光学表征方法,提取和量化粗糙断层模型周围全场主应力差和剪应力的连续分布和演化。刘燕强等利用三维扫描和3D打印技术制作透明的粗糙度节理试件,实现了剪切过程中结构面接触分布的可视化。但是,如何定量、全面地分析接触面积和接触应力等特征仍需深入研究。
数值模拟具有可视化的优点,可以实时定量地反映出结构面接触情况。但考虑到计算效率,以往学者的研究主要集中于二维或规则的三维结构面,无法很好地还原结构面的真实剪切行为。针对三维粗糙结构面,FATHI等和XIAO等分别提出一种新的数值模拟方法来描述剪切过程中粗糙结构面接触面积的变化,但却难以表达接触应力。进一步的,NGUYEN等和DANG等利用FLAC进行了粗糙结构面的直剪模拟,不仅直观展现了剪切过程中的接触面积的变化,还反映出剪切过程中的接触应力状态。但是,由于软件自带INRTERFACE本构模型并未考虑结构面粗糙度的退化,因此该方法仅适用于研究结构面粗糙度未退化或仅有少量破坏的情况。
综上可见,虽然目前的研究成果可以一定程度上捕捉到岩体结构面三维表面的动态接触特征,但尚无法满足结构面剪切特性的研究需求。鉴于此,笔者首先修正了FLAC软件自带的INTERFACE本构模型,使其能够准确表达粗糙结构面在剪切过程中的力学行为;然后,研究了剪切过程中结构面接触和受力的分布及其演化规律,以及法向应力和JRC对接触特征的影响规律;最后,通过分析结构面表面形貌-接触特征-剪切应力3者间的关系,揭示了结构面剪切应力演化机理。
1 结构面本构模型的修正
1.1 自带INTERFACE模型的不足
FLAC中提供了INTERFACE来模拟节理、断层或层面等可能发生滑动或分离的弱面。INTERFACE是以库仑滑动或拉剪切结合为特征的分界面,其具有摩擦力、黏聚力、剪胀、法向和剪切刚度、拉伸和剪切黏结强度等特性。INTERFACE的剪切行为由摩擦力、黏聚力和剪切刚度等决定。INTERFACE单元无法承受拉力,如其所受法向力为拉力或0,则剪力也为0,这是符合实际的。INTERFACE中采用线性库仑抗剪强度准则作为界面滑动的判断准则,其表达式为
=+tan
(1)
式中,为最大剪力;为黏聚力;为分界面节点相关联的面积;为法向力;为摩擦角。
根据库仑抗剪强度准则可知:当INTERFACE所受剪力超过设定的最大剪力后,界面将产生滑动。如图1所示为通过室内试验和数值模拟得到的法向应力2 MPa条件下的光滑结构面和粗糙结构面的剪切位移-剪切应力曲线,试验和模拟方法详见第3章。由图1可看出,当结构面光滑时,采用自带INTERFACE模拟得到的剪切位移-剪切应力曲线与室内试验较为一致;而当结构面粗糙时,2者则有较大差异,模拟曲线在应力峰值后未出现明显的应力跌落,应力降低速度缓慢。显然,自带INTERFACE尚无法准确模拟粗糙结构面的剪切行为。

图1 岩石结构面剪切位移-剪切应力曲线对比Fig.1 Comparison of shear displacement-shear stress curves of rock discontinuity
粗糙结构面在剪切过程中伴随着结构面凸起的啃断或摩擦破坏,而这种结构面的损伤行为在INTERFACE所采用的线性库仑抗剪强度准则中未得到考虑,进而导致模拟结果与实际产生偏差,具体表现为结构面峰后剪切应力偏大。这正是由于通常情况下,结构面凸起的啃断破坏发生在剪切应力峰值之后。因此,FLAC自带INTERFACE仅能够较好地模拟结构面的峰前剪切行为,但无法很好地模拟结构面的峰后剪切行为。然而,真实的岩体工程环境中,绝大多数结构面都具有一定的粗糙度,并且会在剪切滑移中产生显著的损伤。此外,岩石结构面的峰后剪切行为对工程围岩稳定性控制等也具有重要意义。鉴于以上认识,需对FLAC中自带INTERFACE的本构模型进行修正,以期提高结构面剪切行为数值模拟的准确性。
1.2 模型修正
结构面的剪力由其黏聚力和摩擦力提供。以往学者研究表明:当岩石单元被判断发生破坏后,应将其黏聚力降为0。这对于描述结构面剪切过程中的凸起破坏行为同样是合理的。如图2所示,当结构面凸起发生破坏后,破坏部分的黏聚力将不再发挥作用,结构面的抗剪力完全由摩擦力提供。因此,在数值模拟中当判断得到INTERFACE单元破坏后,需将其黏聚力降为0,之后INTERFACE的剪力完全由摩擦力提供,计算公式为
=tan
(2)
式中,为结构面剪力。
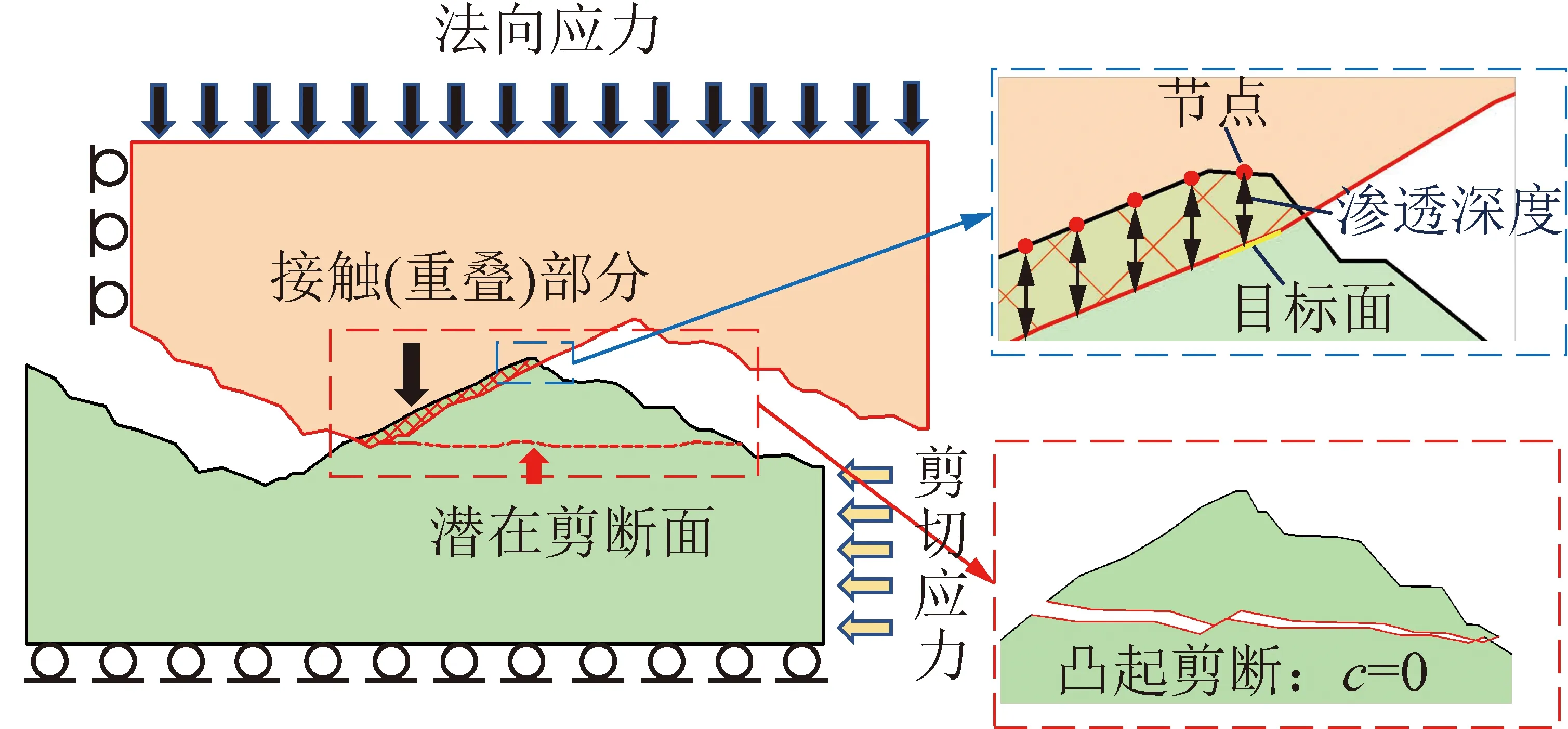
图2 岩石结构面剪切破坏特征示意Fig.2 Schematic diagram of shear failure characteristic of rock discontinuity
由式(2)可知,结构面的剪力与其法向力呈正相关关系,INTERFACE中节点法向力的计算公式如下:
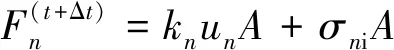
(3)
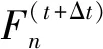
由式(3)可以看出,INTERFACE节点的法向力与节点渗透到目标面的绝对值深度相关。由图2可见,自带INTERFACE未考虑结构面凸起的破坏,导致凸起处节点的渗透深度偏大,进而造成法向应力偏大,甚至超过岩石的抗压强度,如图3所示。可以看出,结构面法向应力的最大值为74.12 MPa,远高于选用材料的单轴抗压强度38.29 MPa,与实际明显不符。JING L等认为作用在结构上的法向应力上限应为岩石的单轴抗压强度。这同时进一步说明了自带INTERFACE无法很好地模拟粗糙结构面的剪切行为。

图3 INTERFACE法向应力分布特征Fig.3 Normal stress distribution characteristic of INTERFACE
综上所述,FLAC自带INTERFACE无法很好地模拟结构面的峰后剪切行为,是由于结构面凸起未啃断导致黏聚力和法向应力偏大。但是,由于FLAC采用的是有限差分方法,其无法实现单元体的破坏分离,此处即凸起啃断。因此,笔者采用等效方法模拟结构面凸起的破坏,其具体修正流程如图4所示(0为初始法向刚度;为时间步数)。首先建立模型并赋参,施加边界条件之后开始进行剪切。每进行一步剪切时,首先需要判断剪切位移是否到达目标值(10 mm),当剪切位移还没到达目标值时,开始遍历INTERFACE单元进行破坏区域监测及变参,即从INTERFACE的第1个单元=1开始(共个单元),通过摩尔库仑强度准则对INTERFACE的破坏区域进行判断识别,当被判别为破坏区域后对其力学参数进行修正,包括INTERFACE单元的黏聚力和法向刚度,然后进入到下一个INTERFACE单元即=+1单元,而当未被判别为破坏区域时则直接跳到下一个INTERFACE单元,直到遍历整个INTERFACE的单元即>后退出破坏区域监测及变参部分。之后再进行下一步剪切,直到剪切位移达到目标值(10 mm)以后结束程序。通过以上修正方法,可使节点的剪力和法向力更接近实际情况,进而能够更好地模拟出粗糙结构面剪切过程中抗剪强度的变化过程。
结构面凸起单元的破坏条件为INTERFACE剪力学行为修正中首要待解决的问题。在以往学者的研究中,通常将摩尔库仑强度准则和最大拉应力准则作为岩石损伤的判断准则,其表达式为
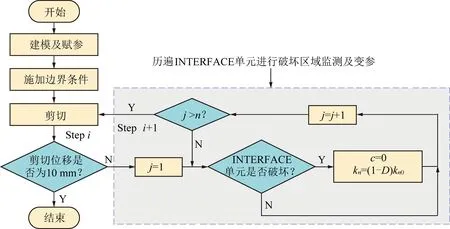
图4 INTERFACE剪力学行为的修正流程Fig.4 Correction process for the shear mechanical behavior of INTERFACE
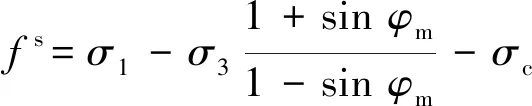
(4)
=-
(5)
式中,和分别为岩石的抗压强度和抗拉强度;为剪切破坏判断函数,当>0时单元体发生剪切破坏;为拉伸破坏判断函数,当>0时则单元体发生拉伸破坏。
针对结构面破坏区域的法向受力问题,为了使模拟中INTERFACE破坏凸起单元的法向力更符合实际。借鉴相关文献[44-45]中模拟岩石损伤的方法,通过赋予损伤因子来降低破坏单元的法向刚度,从而降低结构面法向应力,其计算公式为
=(1-)
(6)
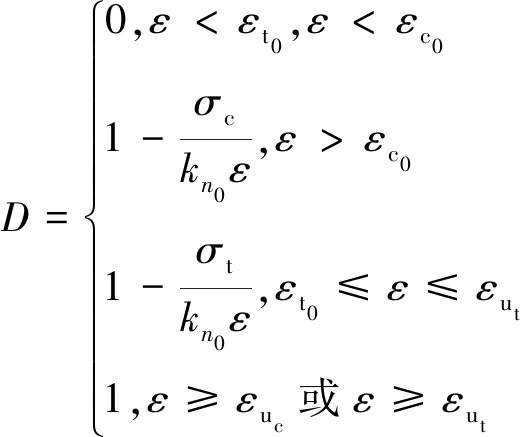
(7)
式中,为节点法向应变;c为抗压峰值强度时的应变;t为抗拉峰值强度时的应变;u为极限抗拉应变;u为极限抗压应变。
2 模型验证
为验证上述INTERFACE修正模型在模拟结构面剪切行为方面的准确性,开展室内试验以进行对比验证。
2.1 室内试验方法
室内试验结构面试件的尺寸为200 mm(长)×100 mm(宽)×100 mm(高),采用类岩石材料制备,该材料质量配比为高强石膏∶水∶缓凝剂=1∶0.2∶0.005,其单轴抗压强度和弹性模量分别为38.29 MPa和46.55 GPa。试验中选取了表面形貌特征如图5所示的3类具有不同粗糙度的结构面J1,J2和J3作为试件浇筑的模板,它们的粗糙度系数(JRC)分别为3.68,6.18和9.86。制作时首先使用复制花岗岩节理表面形态的硅橡胶模具浇筑上部试件,再以上部试件为模具浇筑下部试件,从而保证上部试件与下部试件吻合,试件浇筑完成后进行14 d的养护即可开展剪切试验。加工完成的试件如图6所示。

图5 不同粗糙度岩石结构面的表面形貌Fig.5 Surface topographies of rock discontinuity with different joint roughness coefficients

图6 制作完成的粗糙岩石结构面试件Fig.6 Completed rough rock discontinuity specimens
室内剪切试验在如图7所示的自主研发的MIS-233-1-55-03型法向应力伺服控制剪切试验系统上开展,该剪切试验系统的指标参数及试验方法详见文献[47]。剪切试验采用恒定法向应力边界条件,考虑到常见锚固工程支护一般位于地下巷道、硐室等围岩2~3 m以浅的范围内,范围内的围岩应力远低于原始地应力,根据相关经验,选取法向应力分别为1,2,4 MPa。试验时,首先以0.5 MPa/min的加载速度在剪切盒上方施加初始法向应力至给定值,然后以0.5 mm/min的速度在下部剪切盒上施加剪力至剪切位移达到10 mm。
2.2 数值模拟方法
为建立具有结构面表面真实形貌的数值模型,首先将利用三维激光扫描技术获取的表面形貌数据转化为ASCII格式,然后将其导入FLAC中,建立与室内试验中试件尺寸一致的数值模型,如图8所示。模型中共包含57 600个单元体和64 294个节点,单元体的平均尺寸为2.5 mm×2.5 mm×2.5 mm。在模型上下两块体间建立INTERFACE,模拟结构面剪切过程中的滑动力学行为。岩石块体选用摩尔库仑本构模型,相关参数通过试验测得;结构面选用修正的INTERFACE模型,相关参数通过“试错法”确定;岩石和结构面的物理力学参数见表1。数值模型的边界条件与室内试验相一致,即在模型顶面施加恒定法向应力,模型底面在法向方向上固定,上部块体右侧在剪切方向上固定。待对模型施加法向载荷并计算达到初始平衡后,通过给下部块体施加与室内试验相同的水平速度实现结构面的剪切。模拟过程中对结构面的受力变形特征等进行实时监测。以速度加载面上节点的水平位移代表结构面的剪切位移,以INTERFACE上的剪切应力代表结构面自身所受剪切应力,以INTERFACE接触代表结构面的接触状态。

图7 剪切试验系统Fig.7 Shear testing apparatus

图8 岩石粗糙结构面剪切数值模型Fig.8 Numerical model for joints shear of rough rock discontinuity

表1 数值模型中的物理力学参数
2.3 对比验证
采用室内试验和数值模拟得到的结构面剪切应力-剪切位移对比曲线如图9所示。
由图9可以看出,修正模型的剪切应力曲线与试验曲线在不同法向应力条件下都匹配较好,尤其是J1和J2结构面,J3结构面在位移软化阶段模拟应力略大于试验结果。这是由于J3结构面的粗糙度系数大,需建立更精细的网格来还原表面形貌特征,以减小模拟与试验的误差,但这将需要更长的运算时间。
为进一步验证数值模拟的正确性,将室内试验和数值模拟得到的结构面表面特征进行对比。由于试验中无法监测结构面的接触状态,因此,采用试验完成后的结构面破坏图与数值模拟的结构面接触图。以法向应力2 MPa的J3结构面为例,图10(a)为室内试验中的结构面的表面破坏特征示意,其中红色圈出的区域为剪切破坏区;图10(b)为数值模拟中结构面接触分布特征示意,其中不同颜色代表不同的渗透深度,具体在第3.1节中详述。可以看出,两图分布整体上较为接近,但数值模拟得到的接触区域小于室内试验中结构面的破坏区域,这是合理的,因为结构面破坏后不可恢复,而接触区域却一直随着剪切位移发生改变。因此,从结构面破坏情况来看,该模拟方法能够较好地模拟结构面剪切的动态接触特征。
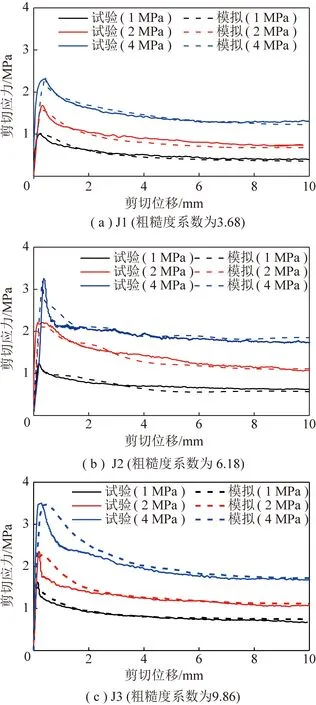
图9 不同粗糙度岩石结构面剪切应力-剪切位移对比曲线Fig.9 Comparison of shear displacement-shear stress curves of rock discontinuity with different joint roughness coefficients

图10 岩石结构面剪切破坏表面特征对比Fig.10 Comparison of surface characteristics of rock discontinuity shear failure
3 数值模拟结果与分析
3.1 接触面积特征及其演化规律
FLAC中结构面的接触状态由INTERFACE的节点和单元体表面的相对位置关系,即模型上部与下部对应节点的高程变化(渗透值)所决定。当INTERFACE的节点穿透单元体表面与单元体重叠,即>0时,INTERFACE单元被认为接触。已有学者指出这些重叠部分可以合理地表示剪切试验中的接触区域。以法向应力2 MPa的J3结构面剪切位移为3 mm时的接触情况为例进行说明。图11(a)为结构面的接触分布;图11(b)为接触的渗透深度,渗透深度为负值表示结构面单元分离;渗透深度大于0表示结构面单元接触。每个INTERFACE节点都关联一定的面积,因此可以采用接触的INTERFACE节点数与总的INTERFACE节点数之比来定义结构面的接触面积比。
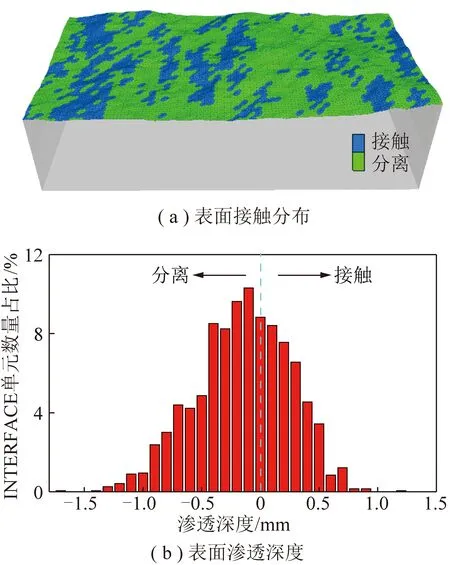
图11 岩石结构面接触分布及其渗透深度Fig.11 Contact distribution and penetration depth of rock discontinuity
剪切过程中结构面接触面积分布演化特征如图12所示,其中上方彩色图为不同剪切位移时INTERFACE的接触分布,白色部分表示分离区域,彩色部分表示不同接触渗透深度的区域(由于渗透深度大于4的数量较少,因此将渗透深度大于4的区域均设为紫色);蓝色曲线代表接触面积比随剪切位移增大的变化规律。可以看出,随着剪切位移增大,结构面的接触面积减小,计算得到的接触面积比也不断减小,但最大渗透深度却不断增加。剪切位移0,0.3,1,3,5,7,10 mm时所对应的接触面积比分别为100%,67.85%,36.70%,24.54%,18.67%,15.34%和11.69%,对应的最大渗透深度分别为0,0.14,0.40,1.13,1.79,2.42,3.35 mm。值得注意的是,结构面接触面积显著减小主要发生在剪切位移0~1 mm,当剪切位移大于1 mm后,减小的速度呈现出显著的下降趋势,节理接触面积比降低很缓慢,这与以往诸多的研究结论相同。

图12 剪切过程中岩石结构面接触面积分布及其演化特征Fig.12 Contact area distribution of rock discontinuity during shearing and its evolution characteristic
图13(a)为不同法向应力条件下J3结构面的接触特征,包括接触分布图和渗透深度频率曲线。由其中的接触分布图可以直观看出,随着法向应力的增大,不仅结构面的接触面积增大,结构面的最大渗透深度也增大。不同法向应力条件下的渗透深度频率曲线形态相近,但随着法向应力的增大,曲线整体上向右偏移,也可证明上述结论。计算得到法向应力为1,2,4 MPa时结构面的接触面积比分别为6.98%,11.69%,21.47%,如图13(b)所示,随着法向应力的增大,结构面接触面积比呈线性增大。结构面的最大渗透深度分别为3.02,3.35,3.68 mm。这主要是由于剪切过程中结构面的接触区域由其表面形貌特征以及剪切方向决定。因此,不同法向应力条件下相同形貌结构面的接触分布相似。但法向应力增大会导致凸起尖端渗透深度增大,进而造成接触面积的增大。
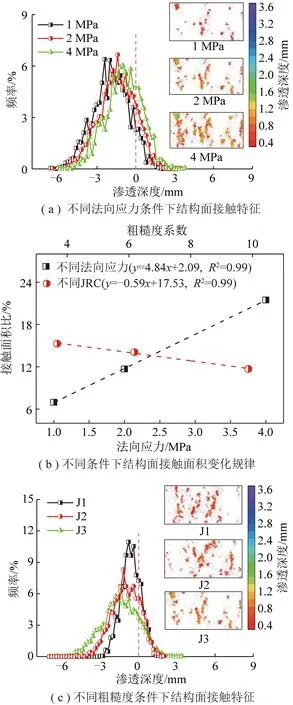
图13 不同法向应力和不同粗糙度条件下岩石结构面接触特征Fig.13 Contact characteristics of rock discontinuity under different normal stresses and different joint roughness coefficients conditions
如图13(c)为法向应力为2 MPa条件下的不同粗糙度结构面的接触特征。由其中的接触分布图可以直观看出,随着JRC的增大,结构面的接触面积减小,但结构面的最大渗透深度增大。不同JRC条件下的渗透深度频率曲线形态差别显著,随着JRC的增大,曲线高度降低,且整体上向两侧扩展,尤其是左侧,这不仅表明了结构面接触面积减小、渗透深度增加,同时也表明了结构面分离程度增加。计算得到J1,J2和J3结构面的接触面积比分别为15.28%,14.07%和11.69%,如图13(b)所示,随着JRC的增大,结构面接触面积比呈线性减小。结构面的最大渗透深度分别为1.42,1.84,3.35 mm。上述现象是由于结构面越粗糙则其剪胀变形越显著,这会导致结构面的接触面积减小,进而造成结构面接触部分应力集中程度高,较大的法向应力会造成渗透深度增大。
3.2 剪切应力特征及其演化规律
结构面的接触特征对结构面的受力分布有较大的影响。由3.1节可知,结构面的接触面积随着剪切运动逐渐减小,而施加在结构面的法向应力将全部作用在接触部分上,进而导致接触区域所受法向应力远高于施加的法向应力,尤其是粗糙尖端的应力,可以达到岩石强度极限状态,并导致这些凸起的失效。图14为法向应力为2 MPa条件下J3结构面在剪切过程中的剪切应力分布及其演化特征,其中彩色图为不同剪切位移时INTERFACE的剪切应力分布,白色部分表示剪切应力为0的区域,彩色部分表示不同大小剪切应力的区域;各曲线代表不同剪切位移条件下剪切应力的分布频率,该曲线是利用自编FISH函数,将结构面上各节点所受剪切应力导出后统计得到的。

图14 剪切过程中岩石结构面剪切应力分布及其演化特征Fig.14 Shear stress distribution of rock discontinuity during shearing and its evolution characteristic
由剪切应力分布可以看出,在剪切初期,结构面完全闭合,剪切应力分布均匀。随着剪切位移增加,在结构面接触分布变化的影响下,结构面剪切应力集中现象越来越显著。剪切位移0,0.3,1,3,5,7,10 mm所对应的结构面最大剪切应力分别为0,3.46,5.37,15.07,17.81,17.81,17.81 MPa。当剪切位移超过5 mm后,随着剪切位移的增大,结构面各单元的最大剪切应力不再增大,但最大剪切应力的分布范围有所增加。由前文INTERFACE模型修正部分可知,当接触部分所受的法向应力超过其抗压强度,会导致其发生法向压破坏,结构面所受法向应力不会超过岩石的抗压强度,且此时已处于残余阶段。结构面抗剪强度由结构面摩擦所提供,当摩擦角一定时,即会产生最大剪切应力。随着剪切的进行,结构面接触范围进一步减小,接触部分应力集中增加,结构面发生法向压破坏的范围增大,进而导致最大剪切应力的范围增大。
由不同剪切位移条件下结构面剪切应力的分布频率曲线可以看出,曲线可以分为低剪切应力区Ⅰ(小于1 MPa)、中剪切应力区Ⅱ(1~6 MPa)和高剪切应力区Ⅲ(大于6 MPa)3个区域。在低剪切应力区内,随着剪切位移增加,节点剪切应力为0的单元的出现频率增大,即结构面分离区域增多,但剪切位移越大变化则越不明显,这是由接触面积变化导致的,与前述接触面积的变化规律相一致。剪切位移为0.3,1,3,5,7,10 mm时,剪切应力为0的单元的频率分别为2.38%,29.72%,67.05%,77.10%,81.97%和86.04%。在中剪切应力区内,随着剪切位移增加,区域内曲线凸起程度不断降低。这是由于剪切位移较小时,结构面接触面积较大,应力集中现象不明显,各单元的剪切应力大都分布在结构面平均剪切应力附近,随着接触面积减小,一方面剪切应力为0的单元数量增加,另一方面应力集中导致高剪切应力的单元数量增加,因而该区域的分布频率显著降低。在高剪切应力区内,剪切应力分布频率曲线近似水平,剪切位移超过3 mm后,随着剪切位移增加曲线变化不显著。
图15(a)为不同法向应力条件下的结构面剪切应力分布特征。可以看出,在结构面接触分布的影响下,随着法向应力的增大,结构面剪切应力分布范围增大,且结构面高剪切应力的分布范围也随之增大,这是由于随着法向应力的增大,结构面两侧岩块嵌入程度更深导致的。剪切应力分布范围的增大和高剪切应力分布范围的增大,是结构面剪切应力随法向应力增大而增大的根本原因。

图15 不同法向应力和不同JRC条件下岩石结构面剪切应力分布特征Fig.15 Shear stress distribution characteristics of rock discontinuity under different normal stresses and different JRCs
图15(b)为J1,J2和J3结构面在法向应力为2 MPa条件下的剪切应力分布特征。可以看出,在结构面接触分布的影响下,随着JRC的增加,结构面的接触面积减小,但高剪切应力的分布范围显著增大,这是由于随着JRC的增大,结构面两侧岩块的嵌入程度更深导致的。剪切应力分布范围对结构面剪切应力影响不明显,高剪切应力分布范围的增大是结构面剪切应力随JRC增大而增大的根本原因。
3.3 结构面接触与表面形貌的关系
GRASSELLI等研究表明,结构面的潜在接触面积与其表面的倾角有关,认为结构面接触区域可以简化为只考虑面向剪切方向且比临界视倾角更大的区域,并提出了新的粗糙度指标来描述接触面积比与临界视倾角的函数关系为
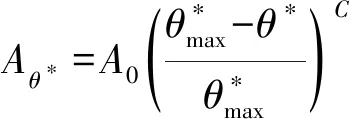
(8)
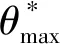
由式(8)可以看出,结构面的接触分布与结构面的倾角分布、临界视倾角有着密切联系。图16为J3结构面在剪切前的视倾角分布,其中白色部分的视倾角小于0°,彩色部分的视倾角大于0°。可以看出,其与图12中的接触区域分布规律大致相同。众多学者研究表明,该指标能够较好地描述结构面形貌与接触的关系。
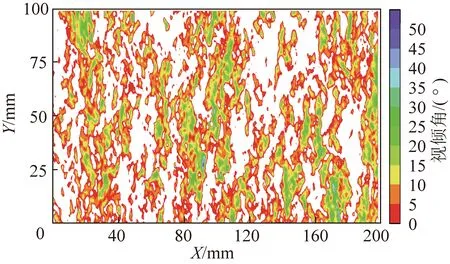
图16 岩石结构面视倾角分布特征Fig.16 Apparent dip angle distribution characteristic of rock joint
结构面的接触面积会随着结构面的剪切位移、法向应力和粗糙度变化,因此临界视倾角在不同条件下的取值也不同。笔者借助数值模拟结果对不同条件下临界视倾角取值的变化规律进行探究,即通过3.1节得到结构面的接触面积比,反算出不同条件下的临界视倾角。其中,J1,J2和J3结构面的拟合参数参照文献[13]的计算方法,其值分别为2.52,2.81,2.34。
图17为法向应力2 MPa条件下J1,J2和J3结构面在不同剪切位移时的临界视倾角。可以看出,从剪切位移为1 mm到剪切结束,J1,J2和J3结构面视倾角的变化区间分别为2.31°~7.60°,3.08°~9.19°和4.92°~14.33°,分别增长了5.29°,6.11°和9.41°。不同粗糙度结构面的临界视倾角都随着剪切位移的增大而增大,临界视倾角与剪切位移呈幂函数关系,随着剪切位移增加,临界视倾角的增加速度逐渐变缓。随着JRC增大,剪切过程中结构面临界视倾角的变化范围增大。
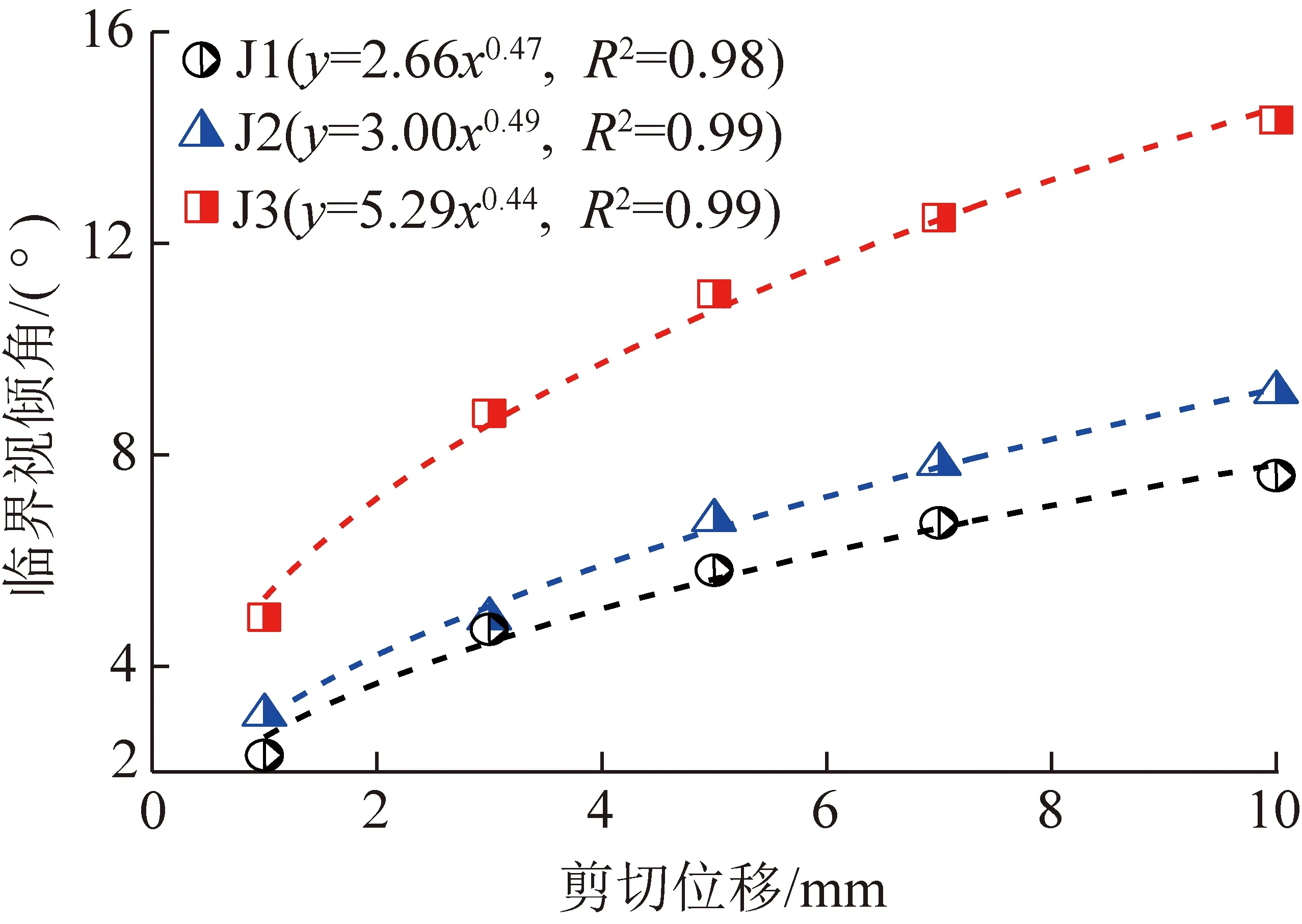
图17 剪切过程中岩石结构面临界视倾角演化规律Fig.17 Evolution of the threshold apparent dip angle of rock discontinuity during shearing
图18(a)为不同法向应力条件下结构面所对应的临界视倾角。可以看出,J1,J2和J3结构面的临界视倾角变化区间分别为9.90°~4.90°,12.33°~5.76°和17.29°~9.92°,分别减小了5.00°,6.57°和7.37°。
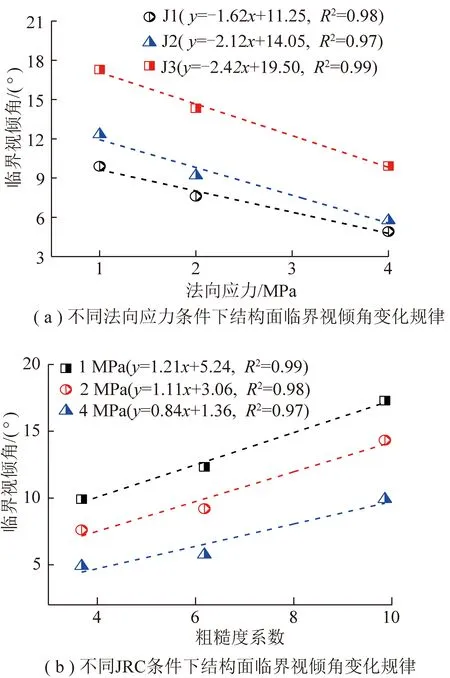
图18 不同法向应力和不同JRC条件下岩石结构面临界视倾角变化规律Fig.18 Evolution of the threshold apparent dip angle of rock discontinuity under different normal stresses and different JRCs
临界视倾角与结构面法向应力呈负线性关系,不同粗糙度结构面的临界视倾角都随着法向应力的增大而减小,且随着JRC的增大,曲线斜率增大,即表明随着JRC增大,法向应力对临界视倾角的影响增大。图18(b)为不同JRC条件下结构面所对应的临界视倾角。可以看出,法向应力分别为1,2,4 MPa的结构面的临界视倾角变化区间分别为9.90°~17.29°,7.60°~14.33°和4.90°~9.92°,分别增大了7.39°,6.73°,5.09°。不同法向应力结构面的临界视倾角都随着JRC的增大而增大,临界视倾角与JRC呈负线性关系,且随着法向应力的增大,曲线斜率增大。即表明随着法向应力增大,JRC对临界视倾角的影响增大。
通过对不同条件下结构面临界视倾角变化规律的研究,可以预测结构面在不同条件下的接触分布情况以及接触面积比,进而建立合理的结构面粗糙度指标以及相关的抗剪强度准则。为此,需要进一步探讨结构面剪切应力与接触的关系。
3.4 结构面剪切应力与接触的关系
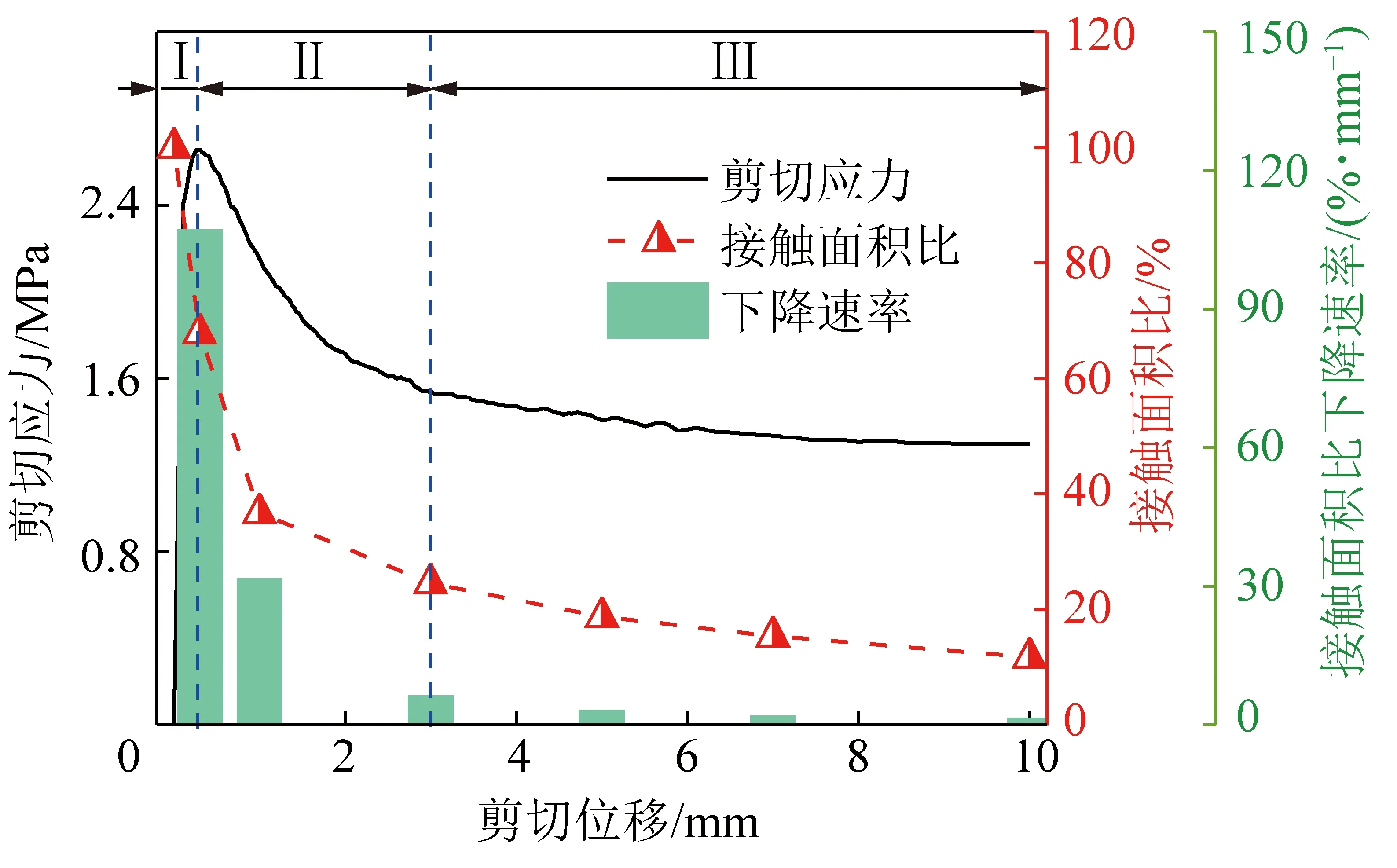
图19 岩石结构面剪切应力、接触面积比及接触面积比下降速率演化规律Fig.19 Evolution of shear stress,contact area ratio and its decline rate of rock discontinuity
结构面的剪切应力由其表面接触部分提供。法向应力为2 MPa条件下J3结构面剪切过程中的剪切应力、接触面积比以及接触面积比下降速率如图19所示。可以看出,在剪切应力峰值前,随着接触面积比的下降,结构面剪切应力仍然继续增大,而在剪切应力峰值后,接触面积比曲线与结构面的剪切应力曲线形态较为一致,2者呈正相关关系。这是由于在剪切应力峰值前,结构面表面凸起尚未破坏,结构面剪切应力由这些凸起提供,凸起处于弹性阶段,结构面的剪切应力随着剪切位移的增加而增加,而当凸起开始破坏后,即进入峰后阶段,结构面剪切应力由少部分未破坏的凸起和接触部分的摩擦提供,并且当剪切位移进一步增大时,结构面接触中的凸起大部分被破坏,结构面剪切应力主要由接触部分的摩擦提供,在峰后阶段随着结构面接触面积减少,结构面剪切应力相应减小。因此,在剪切应力峰值后,剪切应力迅速下降的原因不仅是由于结构面表面凸起的破坏,而且还与结构面接触面积的变化有较强的相关性。
由前文分析可知,结构面接触面积比下降速率可以一定程度上反映结构面发生破坏的情况。由图19中绿色柱可以看出,在不同剪切位移阶段结构面接触面积比下降速率不同,在剪切位移为0.3,1,3,5,7,10 mm时其下降速率分别为83.33%/mm,38.60%/mm,6.08%/mm,2.93%/mm,1.67%/mm,1.22%/mm。即表明结构面接触面积比在弹性阶段Ⅰ下降最快,其次是在位移-软化阶段Ⅱ,残余阶段Ⅲ下降最慢。这是由于,在弹性阶段内,结构面表面凸起未发生破坏,岩块沿着凸起爬坡较为容易,接触面积比迅速下降,但由于该阶段剪切位移较小,接触面积比仍较大;位移软化阶段,由于表面凸起开始被啃断,接触面积比下降速率有所下降,但仍处于一个较高水平,由于该阶段剪切位移较大,接触面积比下降到了较低水平;残余阶段,结构面表面的潜在啃断的凸起基本都已被啃断,岩块运动爬坡现象不明显,而是以摩擦滑移为主,因而结构面接触面积比下降速率变得非常低。
总地来说,上述研究阐明了剪切过程中以及不同法向应力和不同粗糙度条件下的岩体结构面的动态接触特征,揭示了结构面表面形貌-接触特征-剪切应力3者间的关系,深化了对剪切过程中剪切应力演化规律及其机理的认识,可为预测不同条件下结构面的剪切特性提供一定规律性参考。
4 结 论
(1)FLAC自带INTERFACE模型无法很好地模拟结构面峰后剪切行为,是由于结构面凸起未啃断导致黏聚力和法向应力偏大。通过修正INTERFACE破坏单元的黏聚力和法向刚度的等效方法,可很好地模拟结构面的损伤破坏行为。
(2)随剪切位移增大,结构面接触面积逐渐减小,最大渗透深度不断增加;随法向应力增大,结构面接触面积和渗透深度都增大;随JRC增大,结构面接触面积减小,最大渗透深度增大。
(3)随法向应力增大,结构面剪切应力分布范围增大,且高剪切应力分布范围也增大;随JRC增加,结构面剪切应力分布范围减小,高剪切应力分布范围显著增大。
(4)结构面临界视倾角随剪切位移呈幂函数关系增大;JRC相同时,临界视倾角随法向应力的增大而减小;法向应力相同时,临界视倾角随JRC的增大而增大。
(5)结构面剪切应力降低与其接触面积变化有较强的相关性,结构面的接触面积比在弹性阶段下降最快,位移-软化阶段次之,残余阶段最慢。
[1] 班力壬,戚承志,单仁亮,等. 节理峰前剪切刚度软化模型及其影响因素分析[J]. 煤炭学报,2018,43(10):2765-2772.
BAN Liren,QI Chengzhi,SHAN Renliang,et al. Pre-peak shear constitutive model considering the softening shear stiffness and its influencing factors[J]. Journal of China Coal Society,2018,43(10):2765-2772.
[2] 杨小彬,周杰,宋义敏,等. 循环加载岩石界面滑移位移演化特征试验研究[J]. 煤炭学报,2019,44(10):3041-3048.
YANG Xiaobin,ZHOU Jie,SONG Yimin,et al.Evolution characteristics of sliding displacement of rock INTERFACE under cyclic loading[J].Journal of China Coal Society,2019,44(10):3041-3048.
[3] JU Y,WAN C B,REN Z Y,et al. Quantification of continuous evolution of full-field stress associated with shear deformation of faults using three-dimensional printing and phase-shifting methods[J]. International Journal of Rock Mechanics and Mining Sciences,2020,126:1365-1609.
[4] BARTON N. The shear strength of rock and rock joints[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1976,13(9):255-279.
[5] BARTON N,BANDIS S,BAKHTAR K. Strength,deformation and conductivity coupling of rock joints[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1985,22(3):121-140.
[6] XIA C C,TANG Z C,XIAO W M,et al. New peak shear strength criterion of rock joints based on quantified surface description[J]. Rock Mechanics and Rock Engineering,2014,47(2):387-400.
[7] YANG J,RONG G,HOU D,et al. Experimental study on peak shear strength criterion for rock joints[J]. Rock Mechanics and Rock Engineering,2016,49(3):821-835.
[8] KARAMI A,STEAD D. Asperity degradation and damage in the direct shear test:A hybrid FEM/DEM approach[J]. Rock Mechanics and Rock Engineering,2008,41(2):229-266.
[9] ASADI M S,RASOULI V,BARLA G. A laboratory shear cell used for simulation of shear strength and asperity degradation of rough rock fractures[J]. Rock Mechanics and Rock Engineering,2013,46(4):683-699.
[10] BAHAADDINI M,HAGAN P C,MITRA R,et al. Experimental and numerical study of asperity degradation in the direct shear test[J]. Engineering Geology,2016,204:41-52.
[11] ZHAO Z H,PENGP H,WU W,et al. Characteristics of shear-induced asperity degradation of rock fractures and implications for solute retardation[J]. International Journal of Rock Mechanics and Mining Sciences,2018,105:53-61.
[12] MENG F Z,ZHOU H,WANG Z Q,et al. Characteristics of asperity damage and its influence on the shear behavior of granite joints[J]. Rock Mechanics and Rock Engineering,2018,51(2):429-449.
[13] GRASSELLI G. Shear strength of rock joints based on quantified surface description[D]. Switzerland:École Polytechnique Fédérale de Lausanne,2001.
[14] FATHI A,MORADIAN Z,RIVARD P,et al. Geometric effect of asperities on shear mechanism of rock joints[J]. Rock Mechanics and Rock Engineering,2016,49(3):801-820.
[15] XIAO W M,XIAO C C,WANG W,et al. Contact algorithm for determining aperture evolution of rock fracture during shearing[J]. International Journal of Geomechanics,2016,16(3):04015070.
[16] MENG F Z,ZHOU H,LI S J,et al. Shear behaviour and acoustic emission characteristics of different joints under various stress levels[J]. Rock Mechanics and Rock Engineering,2016,49(12):4919-4928.
[17] 崔国建,张传庆,韩华超,等. CNL及CNS条件下结构面剪切特性试验研究[J]. 岩石力学与工程学报,2019,38(S2):3384-3392.
CUI Guojian,ZHANG Chuanqing,HAN Huachao,et al. Experiment study on shear behavior of artificial joint under CNL and CNS boundary conditions[J]. Chinese Journal of Rock Mechanics and Engineering,2019,38(S2):3384-3392.
[18] 尹乾,靖洪文,孟波,等. CNL 和 CNS 边界条件下砂岩宏细观剪切力学特性[J]. 采矿与安全工程学报,2020,38(3):615-624.
YIN Qian,JING Hongwen,MENG Bo,et al. Macroscopic and microscopic shear mechanical properties of sandstone under CNL and CNS boundary conditions[J]. Journal of Mining & Safety Engineering,2020,38(3):615-624.
[19] FAN W C,CAO P,LONG L. Degradation of joint surface morphology,shear behavior and closure characteristics during cyclic loading[J]. Journal of Central South University,2018,25(3):653-661.
[20] 刘新荣,邓志云,刘永权,等. 岩石节理峰前循环直剪试验颗粒流宏细观分析[J]. 煤炭学报,2019,44(7):2103-2115.
LIU Xinrong,DENG Zhiyun,LIU Yongquan,et al. Macroscopic and microscopic analysis ofparticle flow in pre-peak cyclic direct shear test of rock joint[J]. Journal of China Coal Society,2019,44(7):2103-2115.
[21] BARTON N,CHOUBEY V. The shear strength of rock joints in theory and practice[J]. Rock Mechanics Felsmechanik Mécanique des Roches,1977,10(1-2):1-54.
[22] TSE R,CRUDENC D M. Estimating joint roughness coefficients[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1979,16(5):303-307.
[23] GE Y F,KULATILAKE P H S W,TANG H,et al. Investigation of natural rock joint roughness[J]. Computers and Geotechnics,2014,55:290-305.
[24] ZHANG G C,KARAKUS M,TANG H,et al. A new method estimating the 2D Joint roughness coefficient for discontinuity surfaces in rock masses[J]. International Journal of Rock Mechanics and Mining Sciences,2014,72:191-198.
[25] 唐志成,夏才初,宋英龙. 粗糙节理的峰值抗剪强度准则[J]. 岩土工程学报,2013,35(3):571-577.
TANG Zhicheng,XIA Caichu,SONG Yinglong. New peak shear strength criteria for roughness joints[J]. Chinese Journal of Geotechnical Engineering,2013,35(3):571-577.
[26] PARK J W,SONG J J. Numerical method for the determination of contact areas of a rock joint under normal and shear loads[J]. International Journal of Rock Mechanics and Mining Sciences,2013,58:8-22.
[27] LIU X G,ZHU W C,YU Q L,et al. Estimating the joint roughness coefficient of rock joints from translational overlapping statistical parameters[J]. Rock Mechanics and Rock Engineering,2019,52(3):753-769.
[28] ZHAO J. Matching Matching Coefficient (JMC)[J]. International Journal of Rock Mechanics and Mining Sciences,1997,34:173-178.
[29] GRASSELLI G. Manuel rocha medal recipient shear strength of rock joints based on quantified surface description[J]. Rock Mechanics and Rock Engineering,2006,39(4):295-314.
[30] 唐志成,夏才初,宋英龙,等. Grasselli节理峰值抗剪强度公式再探[J]. 岩石力学与工程学报,2012,31(2):356-364.
TANG Zhicheng,XIA Caichu,SONG Yinglong,et al. Discussion about Grasselli’s peak shear strength criterion for rock joints[J]. Chinese Journal of Rock Mechanics and Engineering,2012,31(2):356-364.
[31] 杨洁,荣冠,程龙,等. 节理峰值抗剪强度试验研究[J]. 岩石力学与工程学报,2015,34(5):884-894.
YANG Jie,RONG Guan,CHENG Long,et al. Experimental study of peak shear strength of rock joints [J]. Chinese Journal of Rock Mechanics and Engineering,2015,34(5):884-894.
[32] 陈曦,曾亚武,孙翰卿,等. 基于Grasselli形貌参数的岩石节理初始剪胀角新模型[J]. 岩石力学与工程学报,2019,38(1):133-152.
CHEN Xi,ZENG Yawu,SUN Hanqing,et al. A new model of the initial dilatancy angle of rock joints based on Grasselli′s morphological parameters[J]. Chinese Journal of Rock Mechanics and Engineering,2019,38(1):133-152.
[33] 刘燕强. 岩石结构面剪切全过程的可视化试验方法及试验验证[D]. 绍兴:绍兴文理学院,2019.
LIU Yanqiang. Visual test method and experimental verification for the whole shear process of rock structural plane[D].Shaoxing; Shaoxing University of Arts and Sciences, 2019.
[34] LIU X G,ZHU W C,LI L K. Numerical shear tests on the scale effect of rock joints under CNL and CND conditions[J]. Advances in Civil Engineering,2020,2020:1-15.
[35] MAHDI S,ABBAS T. A numerical study to investigate the influence of surface roughness and boundary condition on the shear behaviour of rock joints[J]. Bulletin of Engineering Geology and the Environment,2020,79(5):2483-2498.
[36] 郭冠龙. 昊锦塬煤矿含充填节理巷道围岩控制技术研究 [D]. 徐州:中国矿业大学,2015.
GUO Guanlong. Controlling technology of roadway surrounding rock containing infilled joints in Haojinyuan coal mine[D].Xuzhou: China University of Mining and Technology, 2015.
[37] 刘新荣,许彬,周小涵,等. 软硬互层岩体结构面宏细观剪切力学特性研究[J]. 煤炭学报,2021,46(9):2895-2909.
LIU Xinrong,XU Bin,ZHOU Xiaohan,et al. Investigation on the macro-meso shear mechanical properties of soft-hard interbedded rock discontinuity[J]. Journal of China Coal Society,2021,46(9):2895-2909.
[38] NGUYEN V M,KONIETZKY H,FRUHWIRT T. New meth odology
to characterize shear behavior of joints by combination of direct shear box testing and numerical simulations[J]. Geotechnical and Geological Engineering,2014,32(4):829-846.
[39] DANG W G,WU W,KONIETZKY H,et al. Effect of shear-induced aperture evolution on fluid flow in rock fractures[J]. Computers and Geotechnics,2019,114:103-152.
[40] 杨建平,陈卫忠,黄胜. 一种岩石统计损伤本构模型的研究[J]. 岩土力学,2010,31(S2):7-11.
YANG Jianping,CHEN Weizhong,HUANG Sheng. Study of a statistic damage constitutive model for rocks[J]. Rock and Soil Mechanics,2010,31(S2):7-11.
[41] ITASCA. FLAC-fast lagrangian analysis of continua in 3 dimensions-theory and background[M]. Minnesota:Itasca Consulting Group Inc,2012.
[42] JING L. Numerical modelling of jointed rock masses by distinct element method for two-and three-dimensional problems[D]. Lulea,Sweden: Lulea University of Technology,1990.
[43] LIAO Z Y,REN M,TANG C A,et al. A three-dimensional damage-based contact element model for simulating the interfacial behaviors of rocks and its validation and applications[J]. Geomechanics and Geophysics for Geo-Energy and Geo-Resources,2020,6(3)1-21.
[44] ZHU W C,WEI C H. Numerical simulation on mining-induced water inrushes related to geologic structures using a damage-based hydromechanical model[J]. Environmental Earth Sciences,2011,62(1):43-54.
[45] LIANG Z Z,XING H,WANG S Y,et al. A three-dimensional numerical investigation of the fracture of rock specimens containing a pre-existing surface flaw[J]. Computers and Geotechnics,2012,45:19-33.
[46] 蒋宇静,张孙豪,栾恒杰,等. 恒定法向刚度边界条件下锚固节理岩体剪切特性试验研究[J]. 岩石力学与工程学报,2021,40(4):663-675.
JIANG Yujing,ZHANG Sunhao,LUAN Hengjie,et al. Experimental study on shear characteristics of bolted rock joints under constant normal stiffness boundary conditions[J]. Chinese Journal of Rock Mechanics and Engineering,2021,40(4):663-675.
[47] JIANG Y,XIAO J,TANABASHI Y,et al. Development of an automated servo-controlled direct shear apparatus applying a constant normal stiffness condition[J]. International Journal of Rock Mechanics and Mining Sciences,2004,41(2):275-286.
[48] 陈曦,曾亚武. 一个新的岩石节理三维粗糙度指标——基于Grasselli模型[J]. 岩土力学,2021,42(3):1-13.
CHEN Xi,ZENG Yawu. A new three-dimensional roughness metric based on Grasselli’s model[J]. Rock and Soil Mechanics,2021,42(3):1-13.
