数学核心素养在数学教学中的渗透探研

朱姗姗

摘 要：数学核心素养是学生经过数学学习活动后，应获得的综合性能力。数学教学不再是仅仅满足于学生单纯的知识增长，而是要提高学生的综合性能力。为提高学生思考的主动性和课堂的互动性，培养学生数学核心素养，教师要更新教学理念，创新教学方法。文章以“商不变的规律”教学为例，研究核心素养中“数学建模”“逻辑推理”和“数学抽象”在教学环节中的设计问题，以渗透“模型思想”，培养学生推理能力，发展学生数学思维，提升学生数学核心素养。

关键词：小学数学;数学建模;核心素养;推理能力;数学思维

中图分类号：G623.5 文献标志码：A 文章编号：1008-3561（2022）09-0136-03

“数学建模”“逻辑推理”和“数学抽象”是数学核心素养的重要内容，培养学生的数学核心素养是数学教学的主要目标。新课标指出，教师要引导学生在现实情境中体验和理解数学知识，用启发式教学方式落实学生的主体地位。在教学中，教师应提出精准高效的问题，引导学生积极主动地寻找解决问题的方法，在真问题、真思考、真探究中培养数学核心素养。本文以苏教版小学数学四年级上册“商不变的规律”为例，对数学教学设计中怎样体现学生的主体地位并发展学生的数学核心素养进行探究。

一、创设情境，渗透数学模型思想

《义务教育数学课程标准（2011年版）》指出，模型思想是学生体会和理解数学与外部世界联系的基本途径。建立和求解模型的过程包括：从现实生活或具体情境中抽象出数学问题，用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律，求出结果并讨论结果的意义。

例如，在教学中，教师可播放动画片《西游记之大圣归来》的片段，引入大圣给八戒分桃的故事。大圣深知八戒贪吃，就给八戒规定25个桃子，平均分5天吃完。八戒掐指一算，每天才能吃5个，连忙说：“啊，不行不行，每天吃得太少了。”大圣又说：“那好吧，我给你50个桃子，平均分10天吃完。怎么样？”八戒挠挠头，试探着说：“大圣，再多给点行不行？”大圣说：“好吧，那就给你100个桃子，平均分20天吃完，这回总可以了吧？”八戒觉得占了大便宜，开心地笑了，大圣也笑了。

设计八戒吃桃情境，可以激發学生学习兴趣，吸引学生的注意力，引导学生带着问题进行学习与思考。学生根据已有知识能想到三次分桃属于平均分问题，应该用除法计算，25÷5=5（个），50÷10=5（个），100÷20=5（个）。不管桃子的总个数和吃的天数如何变化，平均每天吃的个数都是5个。三道算式的商都不变，学生对此存在很大的困惑。总桃子数量和总天数的变化是否有什么规律，才能保证每天吃桃的个数不变呢？在此除法模型中，被除数和除数发生什么变化，商不变？是学生接下来要探讨的问题。

二、自主探究，培养逻辑推理能力

《义务教育数学课程标准（2011年版）》指出，推理能力的发展应贯穿于整个数学学习过程中。推理是数学的基本思维方式，也是人们学习和生活中经常运用的思维方式。推理一般包括合情推理和演绎推理。在小学阶段，学生学习较多的是合情推理，从已知判断推断出未知结论，再进行去粗取精，去伪存真。教师作为引导者必须给学生提供探讨交流的空间，让学生通过观察、实验、归纳、类比等一系列数学活动获得数学猜想，发展完善逻辑推理能力。

例如，围绕“被除数和除数发生什么变化，商不变”这个问题，教师可引导学生观察上面三道算式，初步得出以下猜想。生1：同增同减，商不变。（猜想1）师：具体说说你是如何猜想的？生1：比较算式①和②，被除数由25变成50，增加25，除数由5变成10，增加了5，商不变。反过来被除数由50变成25，减少25，除数由10变成5，减少5，商还是5，没有变化。之所以出现猜想1，是因为学生在学习过程中出现了知识的负迁移，将以往的被减数和减数同时增加或减少一个相同的数，差不变（即同增同减，差不变）与除法算式中的规律相混淆。学生提出该错误猜想时，随即就有其他学生提出不同的意见。一类学生从结论入手证明：比较算式①和②，发现商都是5，但是被除数增加25，除数只增加了5，被除数和除数没有增加相同的数量，即没有同增;还有一类学生从条件入手举例证明：以算式①为例，如果被除数和除数同时增加5，得到算式30÷10=3，发现商发生了变化。因此，猜想1是错误的。在提出猜想并证明的环节中，不管是提出错误猜想的学生，还是证明该猜想错误的学生，都能用精准的语言表达自己的思维过程。在这样的辨析过程中，学生的推理能力逐步得到发展与提高。

经过猜想、验证环节后，有学生在原有猜想上提出新的猜想，并结合三道算式验证。出现了以下情景。生2：被除数和除数每次增加和自己一样大的数，商不变，或被除数和除数每次减少和自己一样大的数，商不变。（猜想2）师：这样的猜想初步验证是正确的，是否还有其他猜想呢？生3：被除数和除数同时乘一个相同的数，商不变;被除数和除数同时除以一个相同的数，商不变。（同样结合三道算式阐释猜想正确）（猜想3）师：也就是说被除数和除数同时乘或除以一个相同的数，商不变。同学们，仔细想想新得到的这些猜想是否有联系？能否将他们转变成一条猜想？同桌交流后，汇报成果。生4：其实被除数和除数每次增加和自己一样大的数，商不变。就是将被除数和除数同时乘2，商不变。同理，被除数和除数每次减少和自己一样大的数，商不变，就是将被除数和除数同时除以2，商不变。这也就是说猜想2是猜想3的一部分，可以合并起来概括为猜想3。师：有道理，但是现在只通过①②③这一组算式就能证明猜想3是正确的吗？这样的猜想是否也适用于其他的除法算式呢？生5：我们可以举例验证。随后，学生通过大量的例子证明猜想3的正确性，得到结论3。师：同时乘或除以的这个数是任意一个数吗？生6：不能是0，因为如果被除数和除数同时乘0，会出现0÷0的算式，在除法算式中，除数不能为0。师：那之前的结论应该如何准确表达？生：被除数和除数同时乘或除以一个相同的数（0除外）商不变。师：这个发现在数学上被称为商不变的规律。

在探索规律的过程中，教师提供充分的探索交流空间，使学生主动参与，乐于探究合作，勤于動脑，动口，经历提出猜想、举例验证、获得结论的探索过程，体验和发现数学规律，发展数学推理能力。

三、练习巩固，发展数学抽象意识

学生在学习过程中能理解数学符号并应用符号进行数学表达，意味着学生的数学思维由具体形象思维过渡到抽象代数思维，这在学生思维发展进程中属于质的飞跃。数学符号是数学语言的表达形式，也是数学计算、推理、交流的工具，用符号表示数、数量关系和变化规律具有简洁性和严密性。因此，培养学生的符号意识在数学学习中显得尤为重要，教师应重视培养学生学会用符号语言精简表达数量关系及变化规律的能力。例如，在“商不变的规律”练习环节，为培养学生的符号意识，笔者设计这样的习题：根据商不变的规律写出三道与4÷1=4商相等的算式。学习并掌握商不变的规律后，学生能够明白和4÷1=4商相等的算式不止三道，还有更多。因此，会出现多种答案。为培养学生的符号意识，教师应相继提问：这样的式子写得完吗？你能用一道式子表示吗？在实际教学中，学生出现了以下答案。答案一，8÷2=4，36÷9=4， 28÷7= 4（4×一个数）+（1×同一个数）。答案二，

其中像“答案一”这样用文字表述的学生较多，但是在出现了“答案二”的这些答案后，通过对比，学生感受到用符号表示数的优势，最终都会选择用符号表示。针对“答案二”的三种情况，笔者选择一个追问： （4×a）÷（1×a）=4，后面的字母a可以换成字母b吗？在这些式子里，出现了字母、图形等符号，学生能够做到有意识地、自发地用这些符号表示数，并且能够意识到同样的字母表示相同的数，不同的字母表示的数不一样。

四、提升训练，增强学生应用意识

要在课堂上真正做到以学生为主体，发展他们的数学核心素养，课程内容必须精心设计，层次分明，每一环节设计意图要明确以确保在实际在教学中取得理想效果。在练习环节，教师可增加提升练习，以培养学生活学活用知识、举一反三的能力。提升练习题的选择可以是针对课堂知识点的拓展，以增强学生的应用意识，让学生将所学知识应用于生活，解决现实生活中的数学问题。因此，在“商不变的规律”拓展练习中，教师可设计如下练习题。

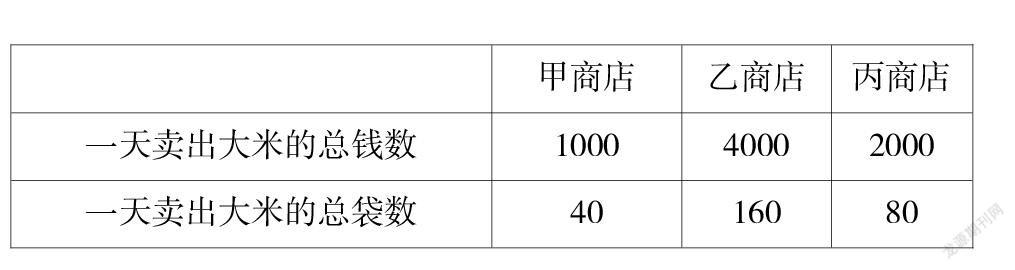
（1）下面是三家商店一天卖出大米的总钱数和一天卖出大米的总袋数情况统计，这三家商店卖出的每袋大米的价格相同吗？试着用商不变的规律解释。

（2）观察300÷25的计算过程，说说这样计算的理由并用相同的方法计算下面各题。

对于习题1，刚开始的设计没有提醒学生用商不变的规律说明原因，发现有部分学生将每家商店的每袋大米的实际价格算出来进行解释。究其原因，学生以往的数学学习很少与现实生活相联系，课堂上没有经常性地训练用数学的概念、规律或方法解决生活中的数学问题。具体计算出每袋大米实际价格的学生，能够将生活实际问题抽象成数学问题加以解决，说明他们具有一定的应用意识。为增强学生的应用意识，练习的设计应明确具体要求，指出思考方向，提示学生“用商不变的规律”解释。

在学生能够独立应用所学知识解决问题前，教师可以通过特例进行引入，引导学生经历由特殊到一般的数学简便计算，切实感受商不变的规律的独特价值，并能在以后的学习中自觉应用。如根据除数是25的特点，将25转化成100进行计算，再运用商不变的规律，被除数300也乘4，于是300÷25的计算即可转化成1 200÷100的口算。在接下来的两道式子中，学生已经学会举一反三，快速口算出两道题的得数。学生通过多方面、多层次、多角度习题的练习与比较，丰富对规律的认识，能自觉将规律的理解与应用内化于心。

综上所述，在日常教学中要想有效培养学生数学核心素养，教师需要做到以下几个方面。首先要创设一定的教学情境，引导学生主动发现并探究问题，进而构建数学模型思想。其次，在课堂探究环节，要引导学生自主推理，鼓励其勇于表达自己的想法，同时尊重学生的解题方法，保证课堂的开放性。再次，要特别注重数学从具体到抽象的转化，将抽象思维内化于心，提高学生对数学问题的认识。最后，通过进阶的训练，将数学核心素养外化于形，增强学生数学应用意识，真正实现“授人以渔 ”。

参考文献：

[1]吴艳.核心素养下小学数学计算教学思考[J].数学学习与研究，2020（23）.

[2]马丽荣.小学数学教学的策略探析[J].吉林省教育学院学报，2020（08）.

[3]沈岷雯.关于小学数学教学与核心素养的融合分析[J].天津教育，2020（21）.

[4]郭见刚.关于小学数学核心素养的实践与思考[J].数学大世界，2020（07）.

[5]刘海花.基于数学核心素养的小学数学教学策略探讨[J].数学大世界，2021（04）.

[6]钱述昶.基于学生数学核心素养培养的小学数学教学探究[J].天津教育，2021（10）.

[7]白建明.如何在小学数学课堂上培养学生的核心素养[J].数学大世界，2021（04）.

[8]周健.在找规律中发展学生的数学素养——以“商不变规律”一课为例[J].数学学习与研究，2018（04）.

Research on the Penetration of Mathematics Core Competence in Mathematics Teaching

——Taking the Teaching "Law of Quotient Ivvariability" as an Example

Zhu Shanshan

（Xianlinhu Campus of Nanjing Jinling Primary School， Nanjing 210000， China）

Abstract： Mathematics core competence is the comprehensive ability that students should obtain after mathematics learning activities. Mathematics teaching is no longer only satisfied with students' simple knowledge growth， but to improve students' comprehensive ability. In order to improve students' thinking initiative and classroom interaction， and cultivate students' mathematical core competence， teachers should update teaching ideas and innovate teaching methods. Taking the teaching of "the law of quotient invariability" as an example， this paper studies the design problems of "mathematical modeling" "logical reasoning" and "mathematical abstraction" in the teaching link of core competence， so as to infiltrate "model thought"， cultivate students' reasoning ability， develop students' mathematical thinking and improve students' mathematical core competence.

Key words： primary school mathematics; mathematical modeling; core competence; reasoning ability; mathematical thinking