霍尔元件在电磁感应实验中的应用

孙晓燕，吴天昊，黄 庆，田永宁，李成金

(苏州城市学院 光电与能源工程系，江苏 苏州 215104)

电磁感应教学中经常用到的一个实验是：分别将非磁体和小磁铁从竖直放置的铝管或铜管等类似的非铁磁金属管的顶端释放(本文实验用的是铝管，以下统称铝管)，观察两种物体在管中下落运动的区别.前者的下落相当于常见的在空气中的自由落体运动.而后者的下落，由于电磁感应和安培力的作用，颠覆了学生已有的认知，从而激发学生试图描述磁体运动规律的好奇心.事实上，定量地描述或测量磁体在铝管中的下落运动，需要用到电磁感应定律、安培定律、牛顿第二定律等定理和霍尔元件、嵌入式系统等知识和技术.

1 实验目的、实验仪器及原理

1.1 实验目的

磁体在铝管中下落时，由于电磁感应在铝管中将产生感应电流，根据楞次定律或安培定律，此感应电流会阻碍磁体的下落，其加速度会变小，但速度会继续增大，感应电流也会增大，当管中的感应电流所受安培力(其反作用力作用在磁体上，方向向上)的大小等于重力时，速度达到最大值vT，并以此速度匀速下落，此速度称为终结速度.本文将通过建立感应电流与磁体相互作用的模型，表征下落磁体所受的力，写出并求解牛顿动力学方程，得到磁体下落的速度与时间的函数关系v(t).从而达到定量描述铝管中磁体下落规律的目的.为了验证所得到的速度与时间关系v(t)的正确性，本文使用霍尔元件为传感器，通过嵌入式系统，实现对磁体速度的测量和速度-时间图像的描绘.本文的具体实验目的如下所述：

1) 通过实验，展示电磁感应现象，并定性地研究铝管中磁体下落的规律，同时强化楞次定律的理解；

2) 通过简化磁体与大块铝材中感应电流(电动势)相互作用的处理，培养学生针对原始物理(或实际)问题建立简化模型并应用物理规律解决实际问题的能力；

3) 通过对下落磁体受力分析，建立动力学方程，并应用高等数学(实际上是引导学生学会查阅数学手册)，求出速度与时间的函数关系v(t)；

4) 通过霍尔元件的使用，使学生了解将磁学量转化为电学量的原理[1]，并给出具体的应用实例；

5) 通过嵌入式系统的使用，使学生了解智能系统在测量与控制中的作用，从而引导学生关注智能制造.

1.2 实验仪器及原理

1.2.1 实验仪器

本实验仪器如图1所示，采用的元件有：1) 边长为a=10 mm的钕铁硼立方磁体(强磁体)；2) 正方形截面的铝管，内边长20 mm，壁厚d1=3 mm或d2=2 mm(可选)；3) STM32嵌入式测量与显示系统，包括27个霍尔元件与27个LED管，HMI液晶显示系统，PCB板；4)三脚架.

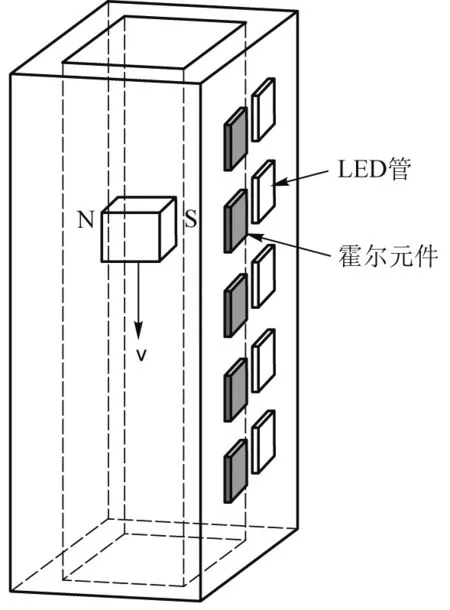
图1 磁体下落示意与测量显示元件

1.2.2 实验原理

1) 建模与动力学方程求解

如图1所示，设磁体的边长为a，质量为m，铝管壁厚为d，电导率为σ.为了建模方便，本实验中将磁体的两极水平放置，设左边为N极，右边为S极，其中心与铝管的截面中心重合，并且磁体的表面与铝管内壁平行.铝管固定于三脚架上，保持竖直.当磁体自铝管顶端入口处释放时，磁体将进入管中.设磁体下落至某一位置时的速度为v，此时磁体左边管壁的磁场区(由磁体形成)的下部的磁场将会由于磁体下落而增加，从而产生逆时针方向的感应电流，此电流在磁场中也会受到向下的安培力，其反作用力作用在磁体上，方向向上，如图2所示.

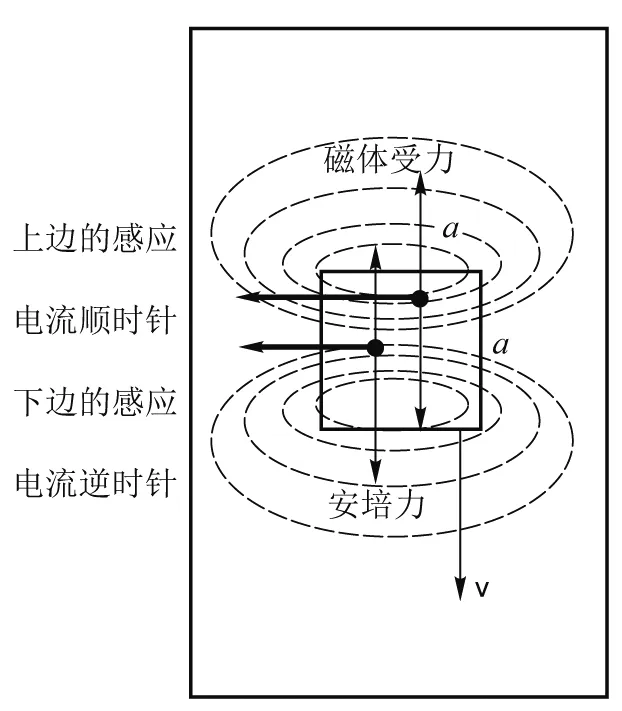
图2 左边管壁的受力分析

同时该磁场区上部的磁场减小，从而产生顺时针的感应电流，此电流在磁场中受到向下的安培力，其反作用力作用在磁体上，方向也向上.而磁体右边的管壁的情况与左边是一样的，磁体所受合力也向上.在理想情况下，磁体上各处所受向上的力相等，因此，磁体在管中保持平动.

根据动生电动势的计算公式，磁体在左、右管壁产生的电动势均为Bav，该电动势在导体中形成涡电流，此涡电流在磁体形成的磁场区域内非常集中，而在其他区域则很分散，以至于在磁体之外的区域电阻可以忽略.于是在涡电流所形成的等效回路中的电阻近似等于磁场区域所覆盖的管壁的电阻R，即

(1)

其中，ρ和σ分别为铝管的电阻率和电导率，且ρ=1/σ，而d为铝管的厚度.于是感应电流的大小为

(2)

此电流所受的安培力为

F安培=BIa=B2σa2vd

(3)

根据前面的分析，此力方向向下，其反作用力作用在磁体上，方向向上，磁体的右面相同.故磁体所受来自于电流的合力为

F=2B2σa2vd

(4)

考虑到重力和牛顿第二定律，可得磁体所满足的动力学方程为

(5)

(6)

上式经过整理和分离变量，得

(7)

式(7)通过积分[1]，并取自然指数，整理得

(8)

式(8)即是磁体下落的速度v与时间t的关系函数，根据此式可得出如下结论：

① 当t=0时，v=0；

② 当时间t增加时，速度随着增加，其v-t曲线如图3所示.

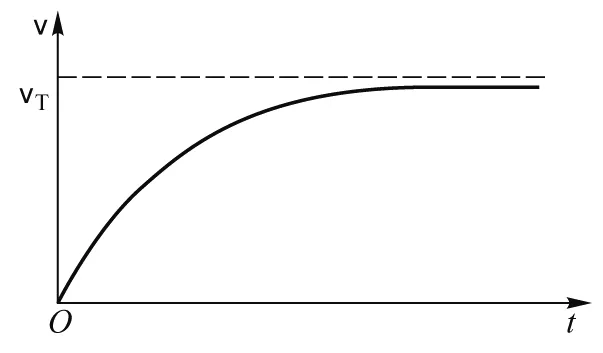
图3 磁体下落的速度与时间的关系

③t→∞时，有

(9)

即速度趋于一个常量，这就是说时间足够长时，磁体将会达到匀速，就是磁体的收尾速度.

④ 在式(8)的e指数中，除了t之外的其它量可用一个参量τ来表示，即

(10)

此参量具有时间的单位，称为系统的时间常量[2].

2) 速度测量系统

从铝管的上端到底部安装细的PCB板，PCB板上每隔50 mm焊接一组霍尔元件与LED管，即为一组测量和显示单元，共27组，期间共计有26个相等的间距(位移，即50 mm)，如图1所示.测量单元之间相互并联后再与直流电源、分压电阻串联成回路，分压电阻两端通过导线接入STM32最小系统，连接HMI屏幕用于显示测量数据，系统以+5 V电源供电，结构框图如图4所示.整个装置固定放置在非铁磁材料的三角支架上.

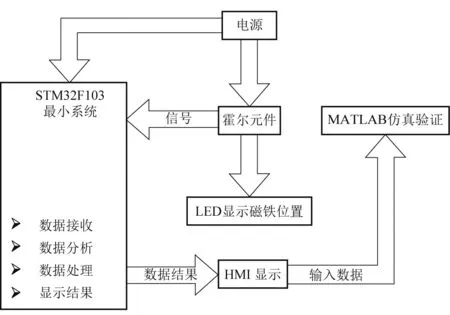
图4 STM32测量显示系统

当磁铁通过霍尔元件时，霍尔元件信号端输出低电平，LED管发光以显示磁体正在经过.通过单片机记录此时的时间，并由程序算出磁体经过相邻两个传感器的时间间隔及通过的平均速度，并在屏幕上显示.

2 实验数据与结果分析

2.1 实验数据

2.1.1 磁体通过每段位移的时间及平均速度

本系统经调试、运行正常后，进行了若干次实验测量，输出数据基本稳定.表1是某次测量的数据记录.

2.1.2 收尾速度与磁感应强度的计算

从表1中的数据可见，磁体通过前三段位移后，速度基本达到了最大值，并趋于稳定，这就是终结速度或收尾速度vT.实验中，本文测量了磁体的质量m、边长a和铝管的厚度d，其数据分别为：m=6.3 g，a=10 mm，d=3 mm.根据商家提供的铝材型号(No.6061系列)，查得本实验铝材的电导率σ为

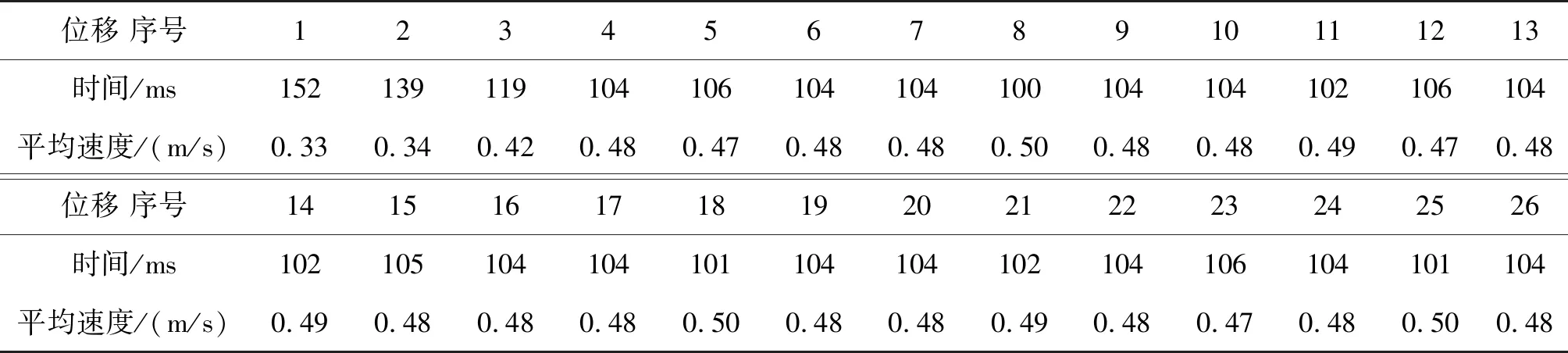
表1 磁体通过每段位移的时间和平均速度(每段位移为ΔS = 50 mm；时间单位：ms)

2.58×107S/m，重力加速度g为9.8 m/s2，将这些数据代入式(9)可算出磁体在铝管内产生的磁感应强度为

9.12×10-2T

(11)

2.2 结果分析

2.2.1 磁感应强度的测量结果与理论值的对比与分析

本文通过简化和建模，导出了磁铁下落的速度时间关系，即式(8)，给出了磁体磁感应强度B的测量或计算方法.通过多次重复实验发现，磁体的收尾速度基本上稳定在vT=0.48 m/s，结合其它数据，算出了磁体在铝管中形成的磁感应强度值为B=9.12×10-2T.由于磁体销售商家不提供相关的数据，从其它资料查得，N3X系列的钕铁硼的剩磁范围为BR=1.13～1.45 T.文献[1]通过COMSOL仿真计算指出，对于剩磁为1.45 T的磁体，其外部的磁感应强度的取值与磁体的大小和考察点到磁体的距离有关，其磁感应强度的范围为B=0.632～0.007 T.显然本实验所测量的磁感应强度，B=0.009 12 T，可见本实验测得的磁感应强度数值处于文献[1]给出的理论数据范围内.具体的根据COMSOL仿真计算数据画出的磁体外磁感应强度的变化曲线请参阅文献1.

应该指出的是，尽管本文所测量的磁感应强度数据处于理论计算(文献1)的数值范围内，由于未查到理论上给出的对应磁体外的磁感应强度准确数据，此处未进行误差计算.

2.2.2 时间常量的结果分析

将本实验的相关测量数据代入式(10)，计算该磁体下落速度变化的时间常量τ为

(12)

从表1中的数据看，磁体下落三段后，即可认为近似达到了匀速(或收尾速度)，所用时间为前三段位移之和，即：Δt=152+139+119 =410 ms = 0.41 s，这段时间差不多是式(12)中建模与实际测量的B算出的时间常量τ的8.3倍，跟理论上达到稳定速度的时间，即5倍的时间常量有一些差距[2].而根据文献[1]给出的磁体外磁感应强度的最小值0.007 T，算出的时间常量约为0.081 s，该时间常量的5倍与实验是基本符合的.

另一方面，本实验建模中做了一些简化，如认为磁场始终垂直于铝管表面，忽略了在厚度3 mm范围内的磁场变化等，这些因素都会使式(12)中的有效磁感应强度变小，因此，实验测量的速度变化规律中的时间常量值大于理论值是可以理解的、合理的.

综上所述，本文认为本实验从对原始问题的建模、计算、系统的搭建，到实验的测量等，梳理出了面对实际问题的解决方案与步骤.由于建模中做了一定的简化，如忽略了一部分电阻、感应电流的非均匀分布、空气的阻力、磁体与管壁的碰撞和摩擦等因素，这些因素都会给实验结果带来误差.表1中的数据也显示了测量数据具有一定的涨落.这表明将一个纯定性实验转变为一个较精确的定量实验还有许多工作要做.

3 结论

本文通过电磁学理论建模和经典力学的动力学方程，研究了磁极沿着水平方向的磁体在非铁磁金属管中的下落情况，得出了速度v与时间t、磁体质量m、磁感应强度B、金属的电导率σ以及一些几何参数的关系.同时导出了速度函数中时间常量τ与上述物理量、几何量的关系.为了验证这些关系，通过设计STM32最小系统，实现了磁体速度、下落时间以及收尾速度的测量.通过这些测量所计算的磁体的磁感应强度B和时间常量τ与理论结果基本符合.