无限深方势阱本征值和本征态的三种求解方法
2022-02-24李海凤陈康康
李海凤,陈康康
(西安工业大学 基础学院物理系,陕西 西安 710021)
一维无限深方势阱是量子力学教材中详细讲解的知识,对广大学生了解量子物理理论具有重要的意义[1-8].虽然它是一个基本且简单的模型,但它的理论结果在许多实际的复杂系统中有着非凡的应用,比如,低维量子受限系统[2].在大多数传统教材中[4-7],只局限于推导一维无限深方势阱,而二维或三维情况较少涉及[8],几乎不讲,并且势阱的边界范围或是(0,a),或是(-a,a).
教材中,一般利用常规方法,即势阱将空间分成几个区间,每个区间求解定态薛定谔方程,利用波函数的标准条件,即相邻两个区域的波函数在边界处相等,可以求出该模型体系的能量本征值和对应的本征态.若势阱左边界为0,求解过程比较简单.若势阱关于坐标原点对称,波函数将分奇、偶宇称两种情况,求解过程变得不那么简单.
本文将超越特殊势阱边界值情况,利用3种不同的方法,推导在任意的势阱边界值情况下,一维、二维、三维无限深方势阱的能量本征值和本征态.
1 三种方法
1.1 常规方法
一维无限深方势阱是一个理想的模型.在一定的约束条件下,许多系统都可以近似为一维无限深方势阱问题来处理.质量为m的粒子被左、右无穷大的势能限定于一维有限的空间[b,c]中运动.设势能函数为

(1)
其中x是粒子在势阱内运动的坐标,如图1所示.

图1 一维无限深方势阱
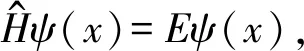
在阱外其他位置,势能无穷大,粒子不可能有概率出现在该范围,则ψ(x)=0.
在b (2) 将上式移项、化简得 (3) (4) 这是一个二阶常系数齐次线性微分方程,通解形式为 ψ(x)=Asin(αx+δ) (5) 根据波函数的单值性和连续性,在势阱边界处,满足ψ(b)=0,ψ(c)=0,即 ψ(b)=Asin(αb+δ)=0 (6) ψ(c)=Asin(αc+δ)=0 (7) 则有αc+δ=nπ,αb+δ=0或αc+δ=0,αb+δ=nπ,其中n=1,2,3,…,每组两式相减,得 (8) 或 (9) 能量本征值为 (10) 将式(8)与式(9)分别代入式(5)得到对应的波函数: (11) 或 (12) 式(12)经过如下推导,比较容易发现与式(11)描述微观粒子的同一个运动状态: (13) (14) 或 (15) 势阱外波函数为0. 下面我们利用一维固定均匀弦振动产生驻波的思想,来解释一维无限深方势阱模型.式(4)的形式解也可以写成如下形式: ψ(x)=Beiα(x-δ′)+B′e-iα(x-δ′) (16) 这是两个运动方向相反的平面波的叠加. (17) 利用边界条件ψ(b)=0,ψ(c)=0,即 (18) (19) 求解上面两式,可以得δ′=b和B′=-B,或者δ′=c和B′=-B.最终对应的本征波函数为 (20) 或 (21) 与式(13)推导思路相似,比较容易得到式(20)与式(21)描述相同的量子态,这里可以将虚单位“i”吸收到波函数前面的归一化因子中,这样我们就得到与第一种方法相同的结果. 根据量子力学传统教材[4-7],势阱范围x∈(0,a),一维无限深方势阱模型能量本征值和对应的定态波函数为 (22) (23) 其中n=1,2,3,….定义新的变量x′=x+b,它的范围是从b到a+b.若c=a+b,则x′∈(b,c).经过变量替换x=x′-b,比较容易得到 (24) (25) 当然,若我们将传统教材中波函数的结果用另外一个势阱边界值表示 (26) 则经过上述变量替换,可以得到任意边界情况下一维无限深方势阱波函数的等价描述: (27) 综上所述,3种方法得到的结果彼此之间相互等价.第1种方法,比较中规中矩,严格求解定态薛定谔方程.第2种方法,利用经典驻波思想,比较直观形象,可加深理解无限深方势阱模型的结果.第3种方法,基于已有结果,通过坐标变换,比较容易得到任意边界条件下的结果.通过上述3种方法,我们比较容易看出,一维任意边界条件无限深方势阱的能量本征值和本征波函数均与阱宽相关. 如图2所示,左边3幅子图,势阱范围是x∈(0.2 nm,0.4 nm),右边3幅子图,势阱范围是x∈(0.3 nm,0.7 nm),自上而下n分别取1,2,3,纵轴是概率密度,即单位体积内发现微观粒子的概率.从左至右,阱宽增加,概率分布形状轮廓不变,峰值降低,变得越来越平缓(或非局域).相反,从右至左,阱宽减小,概率分布形状轮廓不变,峰值升高,变得越来越陡峭(或局域). 图2 一维任意边界无限深方势阱前3个概率密度 通过无限深方势阱模型能量本征值公式,显而易见,随着阱宽增加,能量本征值减少,而随着阱宽减小,能量本征值升高. 除此之外,任意边界无限深方势阱模型的本征波函数与边界值有关,正弦三角函数可以写成坐标变量减去势阱左边界值,也可以写成坐标变量减去势阱右边界值,两种表述等价,描述微观粒子相同的量子态.由于波函数求归一化因子时,只能得到归一化系数的模,其具体表达式不唯一,存在相因子eiφ的不确定性,其中φ∈[0,2π],相因子可任意取值,例如,取±1,±i等. 最终,我们得到任意边界值条件下一维无限深方势阱模型的能量本征值和对应的本征波函数的通式: (28) (29) 或 (30) 二维无限深方势阱是典型的二维受限系统,我们将一维固定均匀弦振动产生驻波的思路拓展到二维情况,将其看成x和y两个维度固定均匀弦振动,在空间相互叠加形成的驻波现象. 如果势阱是二维的,那么势能函数为 (31) 根据定态薛定谔方程: (32) 设定态波函数和能量本征值为 ψ(x,y)=φ(x)φ(y),E=Ex+Ey (33) 利用分离变量法: (34) 通过一维无限深方势阱的结果,比较容易得到二维任意边界无限深方势阱的能量本征值: (35) 和对应的本征态: (36) 其中n1,n2=1,2,3,…,x方向阱宽c1-b1,y方向阱宽c2-b2.对于二维无限深方势阱波函数公式,我们只展示了其中一种表达式,当然也可以用另外一个边界值表示,或者两个边界值均展现在表达式中. 如图3所示,势阱范围x∈(0.2 nm,0.4 nm)并且y∈(0.1 nm,0.5 nm),图3(a)n1=1,n2=2,图3(b)n1=2,n2=1,图3(c)n1=2,n2=2,图3 (d)n1=3,n2=3.综上,我们可以看出不论势阱是长方形,还是正方形,二维受限系统的概率分布图,仍然是驻波图,只是概率分布范围,以及波峰值(概率密度最大值)不同. 图3 二维任意边界无限深方势阱概率密度 如果势阱是三维的,那么势能函数为 (37) 可将三维无限深方势阱模型看作一个在盒子中运动的微观粒子,盒子内粒子感受的势能为0,盒子外粒子感受到的势能为无穷大,粒子完全被束缚在盒子内运动. 与上述计算过程类似,求解得出三维任意边界无限深方势阱的能量本征值为 E=Ex+Ey+Ez= (38) 和对应的本征态为 (39) 其中n1,n2,n3=1,2,3,….c1-b1是x方向阱宽,c2-b2是y方向阱宽,c3-b3是z方向阱宽. 研究三维无限深方势阱,有助于研究高维受限量子系统,并且这类精确可解模型的结果,为发展近似方法提供了比较的基准. 本文通过3种不同方法推导了一维任意边界情况下无限深方势阱模型的本征问题,求解了能量本征值和对应的本征波函数,不同方法得到的结果,彼此之间互相等价.本文的重要结果,得到了一维任意边界无限深方势阱模型能量本征值和本征态的通式,这两个重要的物理量均与势阱宽度有关,并且本征波函数与边界值有关.基于一维情况的结果,我们拓展得到了二维和三维任意边界无限深方势阱模型能量本征值和本征态. 这3种方法对于深刻理解无限深方阱模型具有重要意义.对于简单量子系统模型的研究,为今后研究复杂量子系统奠定了理论基础.希望本文对量子理论的课堂教学及学生对量子力学抽象概念的理解和掌握具有较大帮助.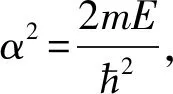

1.2 驻波方法


1.3 坐标系平移方法

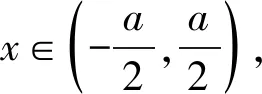
2 二维和三维无限深方势阱
2.1 二维无限深方势阱

2.2 三维无限深方势阱
3 结论
