指向科学思维的习题探究教学实践——以一道全国高考题的探究教学为例

陈志军

（安徽省绩溪中学，安徽 宣城 245300）

1 问题的提出

《普通高中物理课程标准（2017年版）》从物理学科本质的角度说明了物理学科核心素养包括物理观念、科学思维、科学探究、科学态度与责任4个方面，并围绕物理学科核心素养的4个方面设定了高中物理课程目标，这些目标的落实，需要教师引导学生经历知识的形成过程和应用过程来体现.［1］物理习题是学生应用知识、方法的常用素材，物理习题的解决过程是学生运用知识、掌握方法的主要认知过程，是落实物理学科核心素养的主要研究内容.［2］2015年全国卷Ⅱ第21题蕴含着丰富的通过习题教学培养学生形成物理观念、提高科学思维能力的教学素材，本文以此题的探究教学设计与实践为例谈科学思维能力的提升，以期为一线教师的习题探究教学提供参考.

原题.如图1所示，滑块a、b质量为m，a套在固定竖直杆上，与光滑水平地面相距h，b放在地面上，a、b通过铰链用刚性轻杆连接，由静止开始运动.不计摩擦，a、b可视为质点，重力加速度大小为g.则

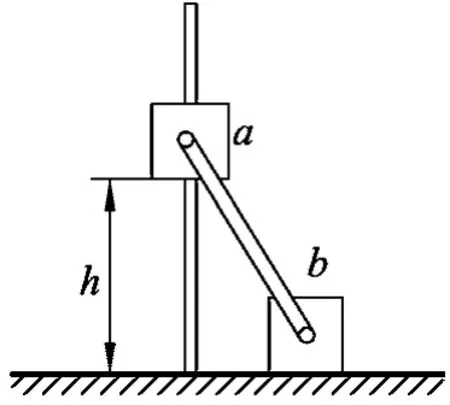
图1

（A）a落地前，轻杆对b一直做正功.

（B）a落地速度大小为

（C）a落地过程中，其加速度大小始终不大于g.

（D）a落地前，当a的机械能最小时，b对地面的压力大小为mg.

解析：本题主要考查牛顿运动定律、速度的合成与分解、功能关系以及机械能守恒定律等知识的综合运用，综合性比较强，难度较大，整个过程都需要严密的推理论证，要求学生具备很强的综合运用物理知识分析问题和解决问题的能力以及较高的逻辑思维能力.

2 探究教学设计与实践

2.1 设计进阶式问题链，强化推理论证

问题设计：在教学过程中，学生对这种试题往往无从下手，出现模型似曾相识、物理规律好像这也能用那也能用、用着感觉又不对的情况，究其原因，是对物理概念和物理规律的本质理解不到位，分析问题和处理问题的能力有所欠缺，推理论证的科学思维方法掌握不够灵活，教学中可设计层层深入的进阶式问题来帮助学生探究.

（1）滑块a、b分别向什么方向运动？做直线运动还是曲线运动？

（2）运动过程中，a、b的速度有什么关系？a落地的瞬间b的速度是多少？

（3）运动过程中，b的动能变化情况怎样？机械能变化情况怎样？

（4）运动过程中，杆对b做功吗？若做功，做正功还是负功？杆对a做功吗？做正功还是负功？

（5）a的加速度比g大还是比g小？

（6）运动过程中，a、b组成的系统机械能是否守恒？a的机械能变化情况怎样？a落地速度大小是多少？

（7）a的机械能最小时，b的机械能怎样？动能呢？速度呢？加速度呢？此时b对地面的压力呢？

设计意图：引导学生找到问题的突破点，首先确定a、b的运动是单方向的直线运动，研究对象是滑块，不是杆；再通过受力分析研究杆的作用，研究杆如何改变a、b的加速度，明确其作用起到牵连作用，得出沿杆方向速度相同的重要结论，并根据滑块的加速或减速来判断杆对两滑块做正功还是负功；最后分析得出系统机械能守恒的结论，进而分析a、b机械能的改变量相同，也反过来根据功能关系理解杆对系统做功情况.用进阶式问题驱动学生推理论证、评价、交流、总结，使学生的思维活动能以习题内容为中心向外展开，探究和寻找解决问题的办法，提升推理能力，培养科学思维.

2.2 设计变式探究，优化思维品质

本题主要是以定性的判断、推理为主，特别是a机械能最小时这一临界点以及该点前后的运动、受力、做功和能量转化等情况，要让学生深入理解该模型的运动过程和各个物理量的变化特点，设计4个变式拓展探究.

变式探究1：将临界点前后分为过程1和过程2，引导学生完成表一的探究问题.

设计意图：引导学生分析推理两滑块的运动情况、加速度、速度、动能、机械能的变化情况以及杆对滑块做功的情况，比较直观地将推理结果呈现，对复杂的运动过程的理解，特别是从全过程来看，虽然通过杆的做功一直在改变b的机械能，但从初、末状态来看，b的机械能并没有变化，因此全过程中只是a的重力势能转化为a的动能，以此巧妙突破问题难点，提高思维品质.

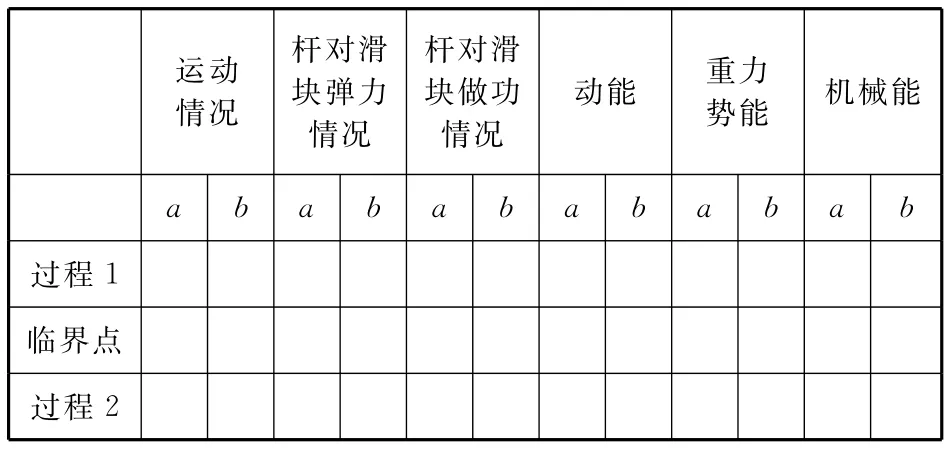
表1 探究问题设计

变式探究2：从分析推论可以得到a的机械能和b的速度、动能、机械能都存在极值，并且对应同一临界点，那么这个极值是否能求出来呢？

设计意图：教学中要引导学生建立模型，设置中间变量，进行定量分析，寻找极值的求解方法，分析时不妨假设杆的长度为l，开始时杆几乎是竖直的，滑块a、b从静止开始运动，根据关联速度关系和系统机械能守恒得出vb2=2glsin2θ（1-sinθ），问题即转化为寻找数学方法处理物理具体问题的阶段，引导学生用不等式求解，分析出当时取极值，此时教师可追问学生临界点前后两个过程中能量转化情况以及功和能的转换关系，以进一步强化推理能力.该探究设计有助于加强学生对运动过程的全面认识，定量分析与处理、极值的确定扫除了学生理解上的障碍.

设计意图：该变式探究设计具有很强的迷惑性，学生开始乍一看以为只有过程2，但只要一分析初始阶段，结果就很明显了.教学中引导学生分析、评价、交流得出此过程实际上是一样的，只是系统具有的总机械能不再是mgl，而是mglsinθ0.

变式探究4：假设小球a并没有套在固定竖直杆上，而是靠在竖直墙壁上，a、b仍通过铰链用长为l的刚性轻杆连接，杆从竖直方向由于扰动，使a开始向下滑动，其他条件均不变，则小球a离开竖直墙壁前，当杆与水平方向的夹角为多大时，其机械能最小？

设计意图：该变式与原题不同点在于a没有被套在竖直杆上，也就是a下落过程中可能脱离墙壁，通过对前面问题的分析，引导学生分析出脱离的临界点，对于临界点以后的情况，与前述问题就有所不同，a离开墙壁以后，水平方向动量守恒，系统的机械能仍然守恒，学有余力的学生，可以进一步探究具体运动情况.

通过变式探究，引导学生对模型进行比较，分析模型的异同点，培养学生的观察能力、分析能力和科学思维能力，促进学生对知识和规律的迁移与应用.

2.3 寻求多种解法，培养创新思维

探究设计：题中杆与水平面夹角θ的临界值的求解，除了利用不等式进行求解以外，是否有其他的办法求极值？

设计意图：引导学生立足于多维、多角度思考问题，探究解决问题的方法，创设分析、讨论、交流的开放性课堂情境，学生自主分析找出其他解法，如利用导数求解，令f（θ）=sin2θ（1-sinθ），则当f′（θ）=0时取极值，也可以得到相同的结论；还可以直接利用机械能守恒求出a的机械能表达式，再利用导数直接求极值.通过多种方法的使用和综合应用，可以复习巩固更多的物理知识内容，关注更多的物理模型和物理过程，跳出传统习题教学模式的弊端，有利于学生在头脑中形成知识结构网络，有利于数学知识在解决物理问题中的应用，并进行知识体系建构，促进深度认知，培养创新思维，提升物理核心素养.

2.4 注重知识迁移，促进深度学习

探究设计：将本题迁移应用到以下新问题.

题1.如图2（a）所示，细线的一端栓一个小球，另一端固定在天花板上.现将细线拉至水平位置，使细线刚好被拉直然后将小球轻轻释放，当细线与水平方向的夹角为多大时，小球重力做功的功率最大？最大功率是多少？

题2.如图2（b）所示，相距为2L的M、N两点处有两个带电荷量均为+Q的点电荷，求两点电荷连线上场强的最大值.

题3.如图2（c）所示，运动员在快艇的水平牵引力作用下，脚踏倾斜滑板在水上匀速滑行，设滑板是光滑的.若运动员与滑板的总质量为m，滑板的总面积为S，水的密度为ρ.当滑板与水平方向的夹角（板前端抬起的角度）为θ时，水对板的作用力大小FN=ρSv2sin2θ，方向垂直于板面，式中v为快艇的牵引速度，S为滑板的滑水面积，求为了使滑板能在水面上滑行，快艇水平牵引滑板的最小速度.

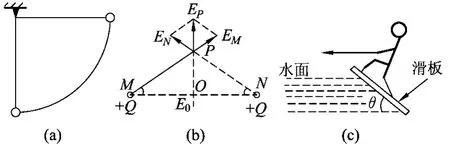
图2

设计意图：题1可设细线与水平方向的夹角为θ，根据机械能守恒和功率的公式，可以得到重力做功的功率，题2可根据场强的叠加原理直接计算两点电荷连线上场强，题3可由平衡条件求解，以上3题都可以得到所求物理量关于sinθcos2θ的表达式，均可以令再利用不等式求解，也可以运用求导的方法进行求解，与前文全国高考原题求极值的方法完全一致.这几道题分别涉及到运动和力、功和功率、电场的性质，虽然是在不同的知识章节，但解决问题的方法都来源于利用相同的不等式或导数求极值，这就要求深度备课时教师对现有的习题资源进行梳理、分类和整合，帮助学生体会物理习题的内容与方法的本质，提升学生对相关物理模型的认知水平，促进学生对相关研究方法的掌握，迁移到相同的物理情境，通过自主与合作学习，迁移所学知识，解决关联的实际问题，实现知识的迁移，促进深度学习.

3 结束语

通过设计进阶式问题链和变式探究强化推理论证，优化思维品质，引导学生尝试多种解法，并迁移知识解决新问题，激发学生探究的意识，提高学生分析问题、解决问题的能力和知识综合运用的能力，促进深度学习，培养科学思维，提升物理学科核心素养.