简明求解浸渐不变量的三步法

陈向正 李 力 王 伟

（重庆市清华中学，重庆 400054）

1 浸渐不变量

当一个周期性运动系统的某个参数发生缓慢变化时，系统可能存在不随时间变化的物理量，［1-2］这个量称为“浸渐不变量”，其英文术语为“adiabatic invariant”.好比水渗透一般的缓慢，“adiabatic”常译作“浸渐”，取“无限缓慢”的意思.［3］

“浸渐不变量”的求解原本是分析力学课程的内容，从哈密顿力学的正则变换出发可以导出浸渐不变量.目前，此类问题已出现在高中物理培优辅导之中.因此，找到一种简洁清晰、易懂易用的初等方法，从而引导学生更容易理解物理本质并求解浸渐不变量，是值得物理教师认真钻研、迫切需要解决的重要课题.文献［4-6］已经给出了一些初等解法，特别是文献［6］为了更适合中学生的学习理解，对初等解法作了一定的改进，但仍然比较繁琐，且思路不够自然清晰，还有进一步优化的必要.

既然由于参数的缓慢变化导致某周期性运动中产生了“不变量”，所以原则上不必考虑任何一个时刻，而只需考虑一个周期内的平均效果，也能找到相应的“浸渐不变量”.遵循这一想法，本文从“微分”、“有效值”、“能量”3个基本概念出发，提炼出一种思路非常自然、更加通俗易懂的“三步法”，能够简明求解浸渐不变量.此初等方法物理本质凸显，物理图像鲜明，数学推导简单，值得向广大中学师生介绍.

2 “三步法”要点

第（1）步微分运算.常用的公式有d（uv）=vdu+udv；若二元函数z=z（x，y），则全微分dz=zxdx+zydy，其中zx、zy分别是z对x、y的偏导数.

第（2）步巧用有效值.由我们熟悉的正弦式交变电流i=Imcosωt的有效值I的定义，显然有故；这个关系可推广至任意对时间t正弦式变化的物理量，即若x=Xmcosωt，则x2对时间的平均值

第（3）步能量守恒.视具体问题的不同，其表达式往往灵活采取不同的形式，如热力学第一定律的形式dE=dW+dQ.

依据前面的想法可知，上面第2步最关键，因为有效值的平方其实就是简谐周期运动物理量的平方的平均值.

3 实例分析

3.1 单摆摆线缓慢收缩过程中的浸渐不变量

例1.如图1所示，单摆的摆线通过一个光滑小孔O，摆球质量为m，重力加速度为g.缓慢拉摆线使其长度l逐渐缩短.设摆动过程中单摆近似做简谐运动，求摆线长度l和摆角幅值θm的关系.

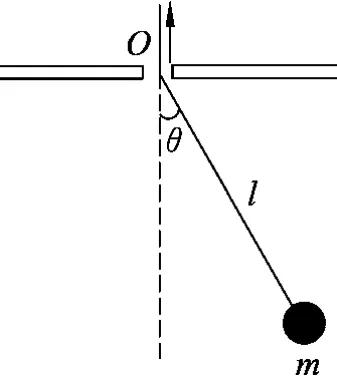
图1 单摆

解析：（1）全微分能量函数.取悬点O所在平面为势能零平面，由于最大摆角θm很小，故简谐运动的能量

注意到右端l、θm是变量，微分得

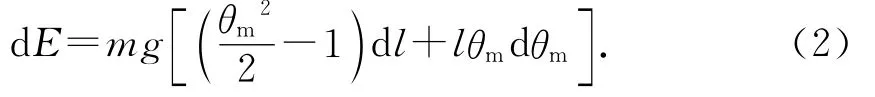
（2）巧用有效值求平均值.在振动中任一位置θ处，线上拉力的瞬时表达式可由向心力公式写出

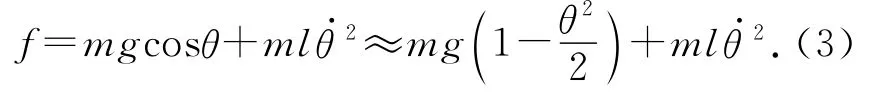
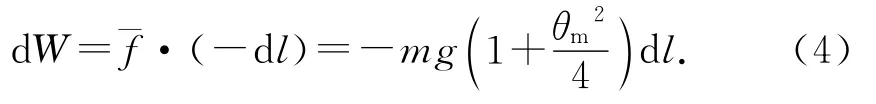
（3）由能量守恒dE=dW，将（2）、（4）式代入化简有3θmdl+4ldθm=0，分离变量积分可得浸渐不变量为

3.2 重力加速度缓慢变化过程中的单摆的浸渐不变量

继例题1，设摆长l保持不变，重力加速度g无限缓慢地增加（可以想象为是单摆在一个加速度缓慢变化的电梯中，以电梯为参考系时，等效重力加速度g缓慢变化），求重力加速度g和摆角幅值θm之间的关系.

解析：（1）全微分能量函数.仍取悬点处为零势能点，E如前面（1）式，但是现在g、θm是变量，由于（1）式中g、l处于交换对称地位，故在（2）式中令l↔g、dl→dg得

由于g的增加导致的能量增加

4 结语

上述两例是文献中比较常见的浸渐不变量问题，例如文献［6］的例题2和例题3.解题时会完整地出现3个步骤.而文献［6］中的理想气体绝热不变量的推导以及例题1，由于不涉及求简谐周期运动中的平均值，所以只会用到“全微分”和“能量守恒”两步，从而更加简单，此处不再赘述.