基于RBF神经网络的三维点云数据孔洞修补
2022-02-24张艺真孙志毅柏艳红
张艺真,孙志毅,柏艳红,王 银
(太原科技大学 电子信息工程学院,太原030024)
基于雷达扫描的三维重构技术,可以较好的实现工程装备作业场景的恢复,对工程应用施工过程中周围环境信息的分析、工程装备的自主作业都具有很大的意义[1]。但在扫描获取点云数据时,往往由于被测物体表面复杂的拓扑结构或者外部遮挡等因素,导致采集回来的点云数据含有孔洞,影响后续重构效果[2]。因此,为了能够准确的恢复出所需物体的形貌特征,需要对点云孔洞进行修补。目前点云孔洞修补基本为两种思路:一种是在三角网格模型的基础上。例如基于变形法的点云孔洞修补方法[3],基于边界特征增长的孔洞修补算法[4],基于泊松方程的三角形网格无缝拼接方法[5]。这些方法通过对散乱点云的三角化处理,完成孔洞数据补测。但是当遇到点云数据量较大且分布不均匀的情况时,往往会出现计算量大,修复效果较差的问题。另一种则是在散乱点云模型的基础上进行修复。例如基于前馈神经网络的孔洞修补算法[6],基于径向基函数的残缺点云数据修复[7],基于径向基函数的三角网格曲面孔洞修补算法[8],文献[7]通过基于径向基函数的插值曲面实现残缺点云修补,但逼近二次曲面点列的误差难以控制[9],文献[8]通过对孔洞区域内不断三角化,来增加孔洞数据填充点,但较为复杂,计算量大。通过对已有补洞算法进行分析,发现径向基函数能够取得较好的补洞效果。
本文以散乱点云模型为基础,在孔洞二维特征平面生成孔洞填充数据点,然后用训练好的RBF网络,预测孔洞区域二维平面填充数据点在三维隐式曲面上的数值,实现孔洞区域的数据修复。通过算例,验证了该方法的实用性。
1 孔洞多边形特征平面的孔洞数据点填充
1.1 孔洞边缘点的提取
边缘点的提取需要满足两个条件,其一是判断在某处法向量是否发生突变,另外还需要判断该点周围的邻域点是否均匀分布。如图1所示,首先需要寻找某点的k邻域点S0,S1,S2,…,Sk-1,S0为采样点自身,分别计算得到S0的法向量n0,及其k邻域的法向量n1,n2,…,nk-1,若n0与其邻近点的法向量n1,n2,…,nk-1的夹角θ大于标准偏差,那么说明该点法向量变化剧烈,暂时认定该点为边缘点。

图1 S0及其k邻域点
另外仍需判断S0周围的邻域点是否均匀分布,将S0与其邻域点的最小二乘特征平面作为投影平面,S0,S1,S2,…,Sk-1在该平面的投影点依次是S′0,S′1,S′2,…,S′k-1,如图2所示,依次连接S′0S′1,S′0S′2,…,S′0S′6,并且S′0S′1与S′0S′4,…,S′0S′1与S′0S′5之间的夹角依次是φ1,φ2,…,φ6,计算两两相邻夹角之间的夹角差,如果差值大于阈值,则说明S0周围的邻域点偏向一侧分布,确认S0是边缘点。
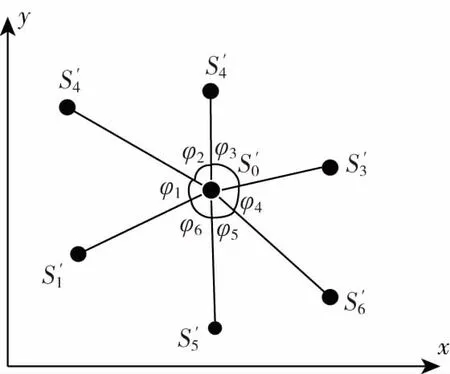
图2 S0及其k邻域点投影图
1.2 特征平面内孔洞数据点的填充
文献[9]利用局部扩张思想,在孔洞区域内不断三角化增加数据填充点,虽然修复效果稳定但计算量大,所以本文提出一种依据边缘点信息并结合蒙特卡罗思想的孔洞数据点的填充算法,该算法更易实现,填充效果较好。
最早的蒙特卡罗法的基本思想,旨在通过随机化的方法计算积分,例如,对于式(1)所示的积分,可以将h(x)分解为函数f(x)与定义在(a,b)上均匀分布的概率密度函数p(x)的乘积,将求积分的问题转换成求f(x)在p(x)分布上的均值,如式(2)所示。

(1)
(2)
此时,可以通过采集大量符合p(x)分布的样本点x1,x2,…,xn,对样本点对应的函数值f(x1),f(x2),…,f(xn)求均值,如式(3)所示,从而解决式(1)的求积分问题。
(3)
本文受蒙特卡罗思想启发,借助计算机在孔洞二维特征平面内均匀投撒大量数据点。以孔洞边界点的分布密度为依据,在平面内沿x,y方向构造网格,保留投撒在网格交点处的数据点,其余数据点删除,完成孔洞区域的数据填充。算法步骤如下:
(1)如图3所示,通过最小二乘法计算获得孔洞边界点的拟合平面π,将提取出来的三维孔洞边界点投影在π上,多边形P1P2P3P4P5为三维孔洞在拟合平面的投影。

图3 孔洞数据点填充
(2)利用计算机在拟合平面π上均匀投撒大量数据点,孔洞多边形P1P2P3P4P5内外均布满密集的数据点。
(3)在平面π上,沿着x轴分别寻找坐标值xmin对应的点P1和xmax对应的点P3,沿着y轴分别寻找坐标值ymin对应的点P4和ymax对应的点P2.连接点P1、P2、P3,沿孔洞边界统计边界线P1P2P3在x轴方向点的数量xn.连接点P2、P3、P4,沿着孔洞边界统计边界线P2P3P4在y轴方向点的数量yn.
(4)计算孔洞边界点在x轴上的分布长度Lx,在y轴上的分布长度Ly.
Lx=xmax-xmin
(4)
Ly=ymax-ymin
(5)
(5)在孔洞多边形P1P2P3P4P5内构造网格。分别在x轴方向和y轴方向求取相邻两点间隔的距离dx和dy.沿着x轴方向,以dx为间隔步长均匀取点。沿着y轴方向,以dy为间隔步长均匀取点,连接成线,相互交叉形成一张网格。
dx=Lx/xn
(6)
dy=Ly/yn
(7)
(6)判断之前投撒点的合理性。筛选之前计算机投撒的点,如果投撒的数据点恰好处于网格的交点位置,那么保留为我们所需要的新增填充数据点,否则将剔除。
2 基于RBF的三维点云孔洞修复
2.1 RBF网络的设计与训练
如图4所示,是本文设计的RBF神经网络的拓扑结构图,隐层径向基函数的基函数是高斯函数[10]。
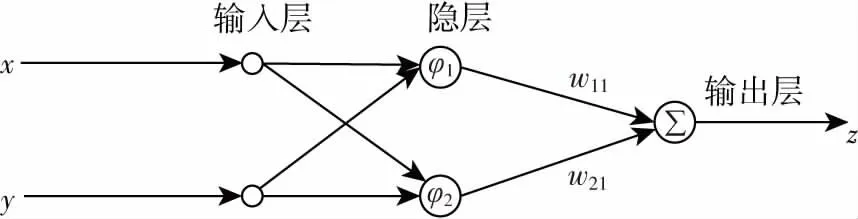
图4 RBF神经网络结构图
函数的表达式为:
(8)
神经网络输出为:
(9)
其中,RBF函数的宽度参数σi,中心Ci,输出单元的权值wki全部从样本中学习获取。
本文设计的RBF神经网络,包含2个输入神经元,1个输出神经元,x,y对应孔洞边缘特征点的x,y坐标集合,z对应孔洞边缘特征点的z坐标集合,以孔洞边缘点为样本,训练优化RBF神经网络的参数。
可以用z=f(x,y)来表示物体孔洞区域的三维表面,在这里认为,训练好的RBF神经网络可以精确的映射样本函数z=f(x,y),准确地表示孔洞区域三维表面的函数形式[11]。
2.2 孔洞待补测数据的生成
之前已经在孔洞多边形的二维特征平面内,获得了与孔洞边界周围密度相一致的新的填充的数据点。训练好的RBF神经网络,在特定误差允许的情况下,认为可以准确的反映孔洞残缺区域的三维表面。因此,借助RBF神经网络,将孔洞二维特征平面内填充的数据点,调整到孔洞残缺区域三维表面上对应的位置,如图5所示。分别将填充的数据点的x,y坐标集合输入到RBF神经网络的2个输入神经元中,网络输出则为残缺区域内补测数据点所对应的三维表面上的z值,完成孔洞区域数据的修复。
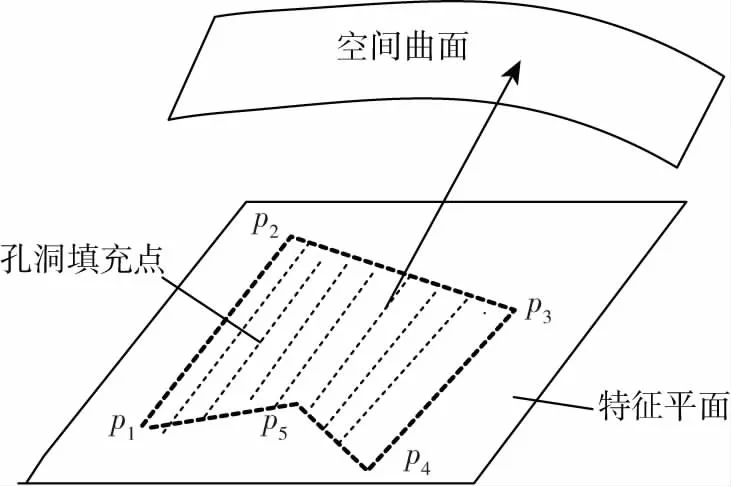
图5 填充点调整至三维表面
3 应用实例
本文在64位windows系统下,以Visual Studio为平台,结合PCL1.8.0点云库以及MATLAB工具完成程序编写。为了验证上述算法的实用性,首先利用16线激光雷达采集工程装备作业环境中具有真实孔洞的土堆、石块点云模型,并以此为例进行修补。
对土堆、石块点云模型的孔洞修复效果分别见图6、图7.
从图6、图7可见,修复后的孔洞区域真实有效的恢复了原有的形貌特征,并且孔洞区域点的密度与边界周围原有点云数据的密度基本保持一致,具有较好的修补效果。

图6 土堆模型孔洞的修复

图7 石块模型孔洞的修复
然后,以斯坦福大学标准库点云模型刀柄和兔子为例,分别对缺失面积较小和较大的孔洞进行修补,修复效果分别见图8、图9.另外以兔子模型为例将本文的修补效果与文献[9]算法的修补效果进行比较。以上算例孔洞修补过程中的相关数据见表1.
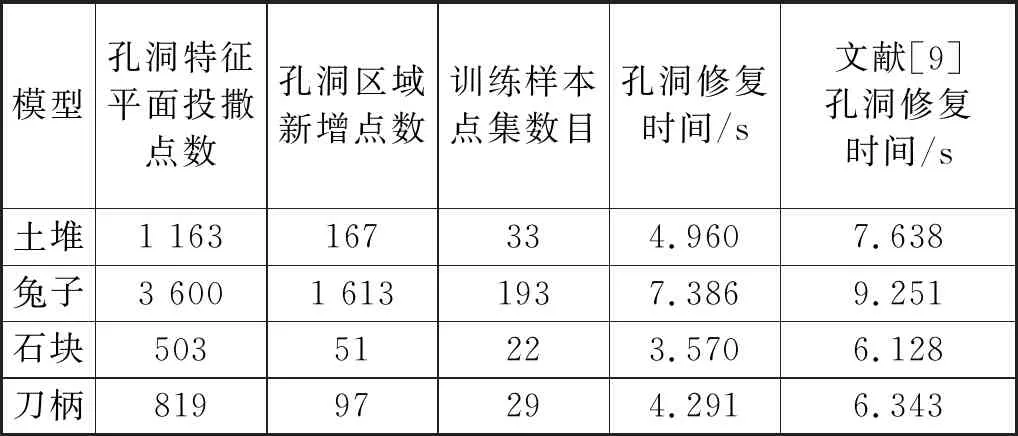
表1 RBF修复孔洞的相关数据
由图8、图9可以看到,无论对于缺失面积较大的孔洞还是缺失面积较小的孔洞,本文算法均具有较好的修复效果,能够反映孔洞区域原有的实际形状。并且与文献[9]算法相比,本文算法在孔洞区域新增的填充点分布更加均匀,补测生成的数据点无论密度还是形状与孔洞周边原有数据更能较好的
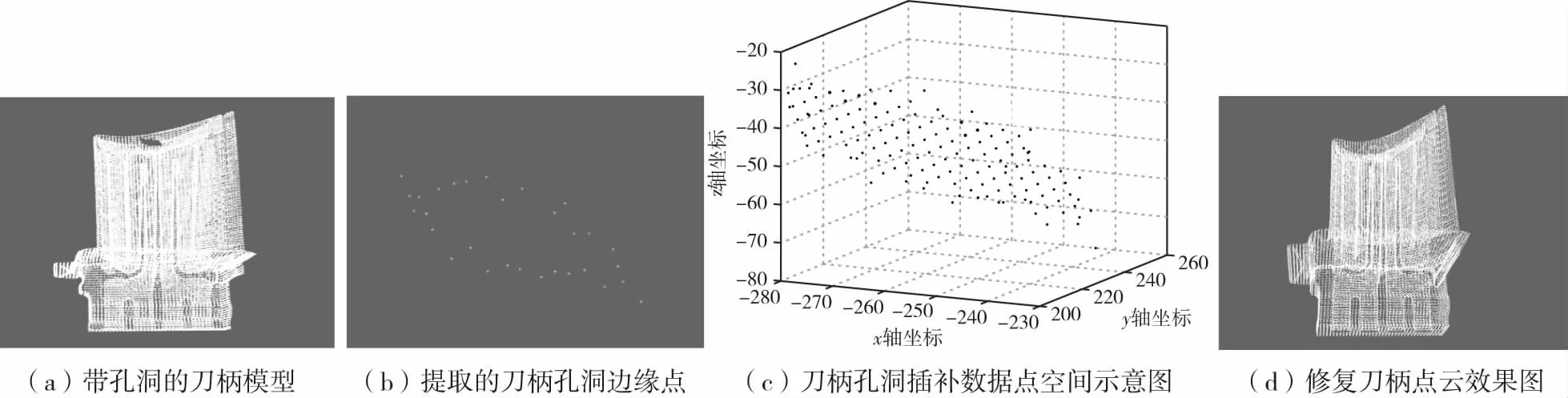
图8 刀柄模型仿真孔洞的修复


图9 兔子模型仿真孔洞的修复
保持一致,过渡平滑自然,修补效果较好。另外,由表1可知,与文献[9]算法相比,本文算法还缩短了三角化填充修复孔洞的时间。通过均匀投撒大量数据点的方法,省去了不断计算填充三角片之间边长和内角关系的过程,减小了运算量。算例结果表明,本文算法在具备较好修复效果的同时,可以提高修复速度,对于流形曲面具有较好的孔洞修复效率。
4 结论
本文提出了一种基于蒙特卡罗法的RBF孔洞修复算法。基于蒙特卡罗法,在孔洞二维特征平面投撒数据填充点,把采集所得孔洞边缘点当作样本点训练RBF,利用训练好的RBF网络将二维特征平面内填充的数据点调整至孔洞区域的三维表面,实现孔洞区域数据的修复。并通过实例验证,该算法可真实有效的恢复孔洞区域原有的形状,并在保障高精度修复效果的同时,提高修复速度,较好的实现孔洞区域的修复。
