尺度自适应的分块核相关滤波目标跟踪算法

张卫峰，何秋生，梁慧慧，贾伟振

(太原科技大学 电子信息工程学院，太原 030024)

作为计算机视觉领域的研究热点，视觉目标跟踪广泛的应用于智能监控、人机交互、军事打击等领域，具有广泛的应用价值和发展前景。由于跟踪环境的复杂性，如遮挡、尺度变化、光照变化、快速移动等因素都会影响算法的性能。

基于深度学习的跟踪算法[1-2]性能较好但是普遍比较耗时，而基于相关滤波器的跟踪算法由于其极快的计算速度和良好的定位性能，也能很好的适应目标外观的变化，因此成为了目前主流的实时跟踪算法。Bolme等人提出的MOSSE[3]跟踪算法，最早将相关滤波器应用到视觉跟踪；CSK[4]跟踪算法是Henriques等人提出的一种高速跟踪算法，利用基准样本的循环移位进行密集采样；随后，Henriques等又提出KCF[5]算法，将CSK算法由单通道扩展到多通道，使其可以使用多维特征，获得更加精确的跟踪结果。但由于是KCF算法中使用了大小恒定的跟踪框，因此不能很好的适应目标尺度的变化，并且没有考虑跟踪过程中目标发生遮挡时的情况。

针对上述问题，一系列基于相关滤波器的改进算法被相继提出。Danelljan等提出CN[6]算法将颜色特征用到目标跟踪任务中，此后又提出DSST[7]算法通过训练尺度滤波器的方法来估计目标尺度。YAO等[8]引入了基于分块的跟踪算法和在线潜在结构化学习，使用全局对象框和少量局部框来近似不规则对象；LIU等[9]在使用KCF方法对子块进行独立跟踪的基础上，通过粒子滤波算法和贝叶斯推理框架来确定目标位置。但上述方法着重于通过分块算法提高算法应对目标遮挡的性能，忽略了目标子块间相对位置变化所隐藏的尺度信息。

由此本文在KCF算法的基础上，提出了一种尺度自适应的分块跟踪算法。为减弱遮挡部分的影响，由局部滤波器提供目标位置的粗略估计，然后由全局滤波器用作初始估计以确定目标的准确位置；同时利用各子块间相对位置的变化来计算目标尺度。

1 核相关滤波算法KCF简介

核相关滤波算法KCF[5]算法凭借极快的运算速度和较高的准确度取得了极大的成功，另外该算法还具有原理容易理解、结构易于扩展等优势。

相关滤波算法中通过样本的循环移位进行密集采样，假设跟踪的目标区域可以表示为一个n×1的一维矩阵，称之为基准样本，Px=[xn，x1，x2，…，xn-1]表示矩阵向右循环移位一次，其中是P一个变换矩阵。因此，所有的循环移位样本{Pux|u=0…n-1}依次排列到同一个矩阵中就可以得到循环数据矩阵X=C(x)，该数据矩阵是一个循环矩阵，具有如下的性质：

(1)

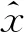
相关滤波算法中将目标跟踪问题转化为求解最小平方误差下的岭回归问题，以此获得最优分类器参数，其目的就是找到一个决策函数f(z)=ωTz，使得样本xi和回归目标yi间的平方误差最小：

(2)

其中，函数f(x)=ωTx可以看作基准样本的线性组合;λ是正则化参数，控制过度拟合；xi表示由基准样本通过循环移位后产生的训练样本；yi为训练样本xi对应的回归目标，并且y服从高斯分布yi∈[0，1].通过求解岭回归问题，可以获得分类器的最优解ω=(XTX+λI)-1XTy，利用循环矩阵对角化性质可以将其简化为：

(3)

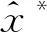
(4)

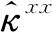
在快速检测过程中，将下一帧中相同位置的图像补丁z视为基准样本，进行快速目标响应检测，可得到时域内输入图像的响应图：

(5)

Pt=argmaxP∈StF(z)

(6)

其中，Pt表示当前帧中目标的中心位置；St表示搜索区域。

2 本文方法

基于分块的目标跟踪方法，在目标被遮挡时仍然能够利用未被遮挡的部分提供准确的定位信息进行跟踪；随着目标尺度的变化，在跟踪过程中各子块间的距离也会相应地发生变化，因此能够根据子块位置变化情况对目标尺度进行估计[10]。

2.1 分块方法

在选择分块方法的时候必须考虑需要使用多少个子块和每个子块设置为多大的问题。当使用的目标块较少时，若目标发生遮挡则会导致获取到的目标信息不够准确；但是使用的子块过多又会使得算法计算量增加。此外，如果子块设置过大，则会使得子块数量减少；当子块设置过小，则会使得单独跟踪每个子块的结果不准确。Liu T等发现子块大小设置为整体目标框大小的1/6到1/4之间时，跟踪结果相差很小，而小于1/6或者大于1/4时，跟踪结果会明显变差。

目前已有的跟踪算法中使用较多的分块策略是将目标划分为四个大小一致的子块[10-11]，如图1(a)所示。此外，还可以根据目标框的纵横比进行子块划分[12-13]，如图1(b)所示。但是，使用以上两种分块方法得到的子块通常包含较多的背景信息，会对跟踪过程造成干扰，从而影响算法性能，因此本文设计了一种能够有效减少背景信息的分块方法。

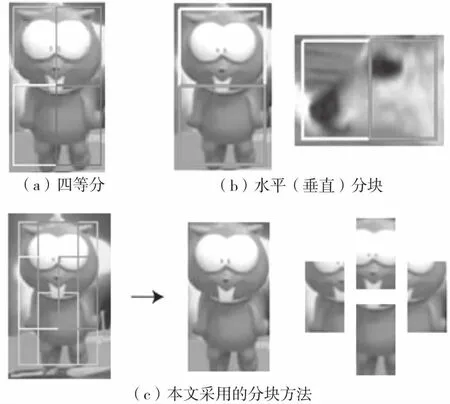
图1 分块方法示意图

本文采用的分块方法，如图1(c)所示，围绕目标中心位置生成四个大小相等的子块。具体为，四个子块的高和宽分别为整体目标框高和宽的0.5倍；上下两个子块的中心坐标分别为以目标中心位置上移和下移0.25h个像素值；左右两个子块的中心坐标分别为以目标中心位置左移和右移0.25w个像素值，可表示为公式(7)：

(7)

其中，m=0.25h，n=0.25w，h和w分别表示整体目标框的高和宽；Pt表示整体目标框的中心位置；Bk表示目标子块的中心位置，k∈(1，2，3，4)表示目标子块的索引。

当目标比较小的时候会导致生成的目标子块太小，不能为目标跟踪提供准确的信息。因此，这种情况并不适合进行分块跟踪：

(8)

其中，当ϑ=1表示需要对进行分块跟踪；ϑ=0时直接对目标整体进行跟踪。ϑ的值由阈值τ决定，经过大量仿真实验发现τ=17时使得跟踪效果最好。

2.2 目标位置确定

本文提出的基于核相关滤波器的分块跟踪方法依赖于全局滤波器和局部滤波器之间的相互作用。为减弱遮挡部分的影响，首先独立跟踪每一个子块，并使用局部滤波器分别计算每个子块对应的响应图，然后从中选取具有最大响应峰值的子块，根据该子块与目标整体之间的位置约束关系初步得到对目标中心位置的粗略估计，最后对估计位置处进行采样并与全局滤波器作用以确定目标的准确位置。

当满足分块条件时，使用核相关滤波算法KCF分别对各个目标子块进行独立跟踪，得到每个子块的响应图Fk，然后选取具有最大峰值的响应图：

k′=argmax(max(Fk))

(9)

(10)

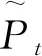
在分类器训练过程中，本文使用了如下的高斯核函数：

(11)

其中，x=[x1，x2，…，xC]表示包含C有个独立通道的向量，通过公式(11)使得在跟踪过程中可以使用性能更好的多通道特征丰富目标的外观表示。

本文中为了更加准确地确定目标中心位置，通过级联31维的梯度直方图特征(Histogram of Oriented Gradient，HOG)和12维的颜色名称特征(Color Name，CN)形成HOG-CN融合特征用于表示目标，然后与核相关滤波器作用计算目标响应，如图2所示。HOG特征描述了图像局部区域的梯度强度和梯度方向的分布情况，CN特征描述了图像的全局表面性质，将这两种特征融合可以利用不同特征间的优势互补来提高跟踪器的性能。

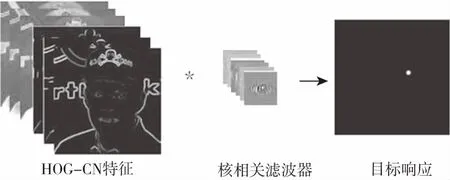
图2 多特征融合算法示意

2.3 目标尺度计算

本文使用的分块跟踪方法，当目标尺度变化范围在0.8～1.2之间时，不对目标进行重新分块，虽然这一尺度变化范围内各子块的目标框大小是恒定不变的，但通过实验发现各子块间的相对位置与目标尺度变化间存在着稳定的关系。当目标尺度变化时各子块间会相应地重叠或分离[13]。如图3所示，第一行中图(a)到图(b)，从第20帧到第147帧，随着汽车逐渐驶远，尺度也随之变小，各目标子块彼此重叠到一起；第二行中图(c)到图(d)，从110帧到138帧，随着目标的尺度变大，各目标子块彼此远离。

图3 子块位置与目标尺度间的关系

本文从这个基本的观测出发，将尺度的计算问题转换为对目标子块跟踪结果的综合问题。

首先，计算当前帧中所有目标子块间中心位置的欧式距离与上一帧中对应子块间中心位置的欧式距离比值的平均值，对目标尺度步长进行粗略估计：

(12)

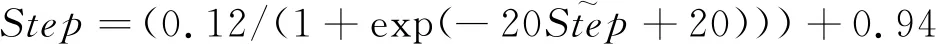
(13)

其中，Step表示尺度步长，即与上一帧相比较目标尺度的变化。前一帧(第t-1帧)的尺度与当前帧(第t帧)中计算得到的尺度步长的乘积即为当前帧中目标的尺度：

St=St-1·Step

(14)

其中，St表示第t帧中目标的尺度参数。

3 实验结果与分析

为对本文算法的有效性进行充分的评估，本文选择包括基础算法KCF在内的5种主流跟踪算法与本文算法在OTB数据集[14]上进行测试，并进行对比分析。本文中参与比较的算法有：CSK[4]，KCF[5]，CN[6]，DSST[7]，Struck[15].所有的算法程序在Windows7系统MatlabR2014a平台上运行，用于对比的算法参数均为作者公布源程序的默认参数，计算机配置为英特尔奔腾G3250 CPU，运行内存4 GB，64位操作系统。本文中使用距离精度(DP)和重叠精度(OP)作为评价指标，具体计算方法见文献[14].

3.1 算法流程

针对目标遮挡情况下跟踪算法性能下降的问题，本文在KCF的基础上改进了一种尺度自适应的核相关滤波跟踪算法，具体的算法流程如下：

Input

当前帧图像It，t=1，2，…，t，…

Output：

检测到的目标位置Pt

尺度参数St

初始帧t=1：

(1)在初始图像帧中选取图像块Patch.

(2)将输入的整体目标图像块Patch分为四个子块。

(3)分别跟踪每个目标子块和目标整体。

其余帧t≥2

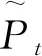
(6)计算目标尺度St.

(7)更新模型参数。

(8)判断St<0.8 orSt>1.2是否成立？成立，则对目标重新分块，然后执行(2)后继续下一步；否，则直接继续下一步。

(9)重复(4)～(8)直到跟踪结束。

3.2 分块方法对比实验

本节中通过四等分和水平/垂直两种分块方法与本文采用的分块方法在本文改进的算法框架中进行比较，为保证测试公平性，除分块方法不同外其余参数设置均一样，并使用距离精度和重叠精度进行评估，实验结果如表1所示。

表1 不同分块方法的比较

通过分析表1可以看出，采用本文提出的分块方法的跟踪效果最好，比四等分和水平/垂直分块的距离精度分别提高了3.9%和3.6%，重叠率精度分别提高了6.6%和4.8%.这一结果证明了本章提出的分块方法与目前常用的分块方法相比具有一定的优势，更有助于提高分块跟踪算法的性能。

3.3 定量分析

首先对本文算法进行总体性能分析。本文算法以及所有比较算法均在OTB2013数据集上进行测试，以距离精度(DP)和重叠精度(OP)作为评判标准，实验结果如图4所示。由图4可见，本文算法在整体性能测试中综合性能排序第一，展现了出色的总体性能。具体的数据为位置误差阈值为20时对应的距离精度为0.811，重叠阈值为0.5时对应的重叠精度为0.686，与基础算法KCF相比跟踪距离精度提高了7.4%，重叠精度提高了7.8%.总的来说，本章提出的算法综合性能比改进之前有了较大的提升。

图4 不同分块方法的比较

为验证本文算法在不同干扰因素下的性能表现，将本文算法以及所有比较算法在遮挡、尺度变化等6种不同属性的视频序列子集上分别进行测试，并将测试得到的距离精度曲线和重叠精度曲线中的数据进行归纳，结果如表2和表3所示，其中表现最好的算法用红色加粗字体标注。

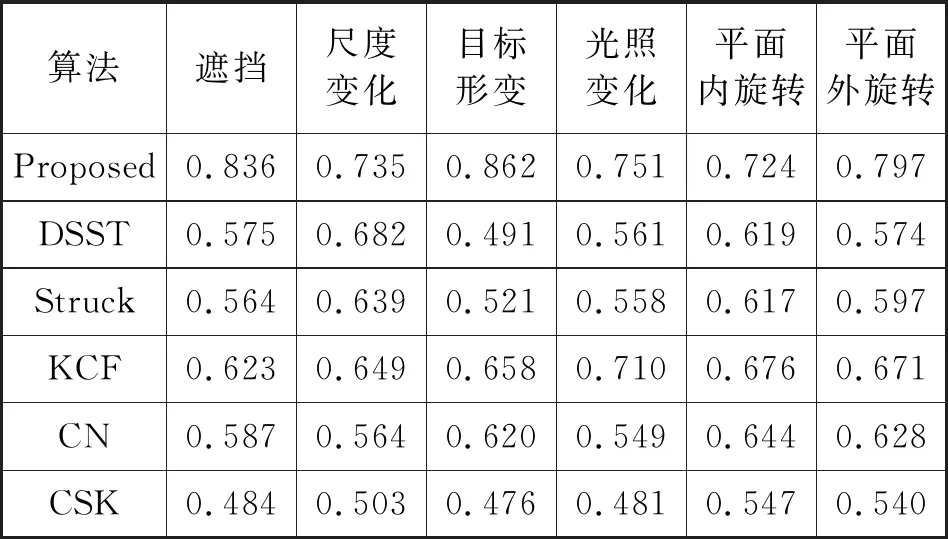
表2 不同属性下的距离精度曲线图数据

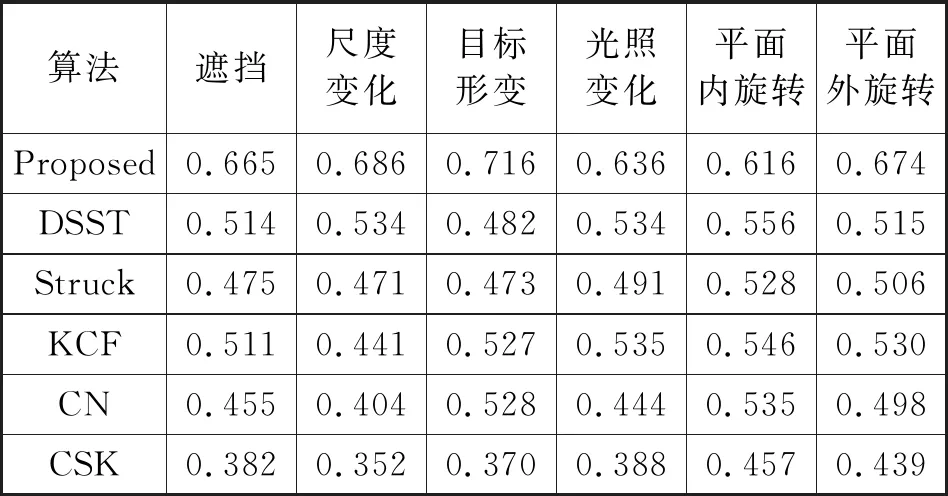
表3 不同属性下的重叠精度曲线图数据

通过分析表2和表3可以得到以下结论：

(1)在遮挡情况下，本文算法与其他对比算法相比其距离精度和重叠精度都是最高的，主要原因是本文提出的分块算法能够在目标被部分遮挡的情况下能够充分利用未被遮挡的目标信息。

(2)在目标尺度变化情况下，本文算法的跟踪精度和重叠精度依然是十种算法中最高的，主要原因是本文算法加入了基于子块跟踪结果计算目标尺度的方法。

(3)本章提出的算法在5种场景属性下的距离精度和重叠精度均取得了最优的结果，说明本文算法在应对复杂场景时具有较好的鲁棒性。此外，除了能够很好地处理遮挡和尺度变化的情况外，在目标发生形变时，该算法也有非常出色的表现。

为评估算法的实时性，本文测试了各个算法在OTB数据集的不同视频序列上运行的平均跟踪速度，实验结果如表4所示。

表4 各算法的平均跟踪速度

由表4可见，相比于原始算法KCF，本文算法使用了HOG-CN融合特征并引入了分块跟踪策略后跟踪平均速度为33.5帧/s，仍能够保持算法的实时性需求。

综上所述，说明本文提出的算法具有非常好的鲁棒性，能够应对绝大部分的挑战。在应对目标遮挡、尺度变化和变形的情况时的性能有非常显著的提升。

3.4 定性分析

为了更加直观地展示本文算法的跟踪情况，图6给出了本文算法和其他5种主流跟踪算法的跟踪结果比较，图5中第一到第四行分别对应Jogging-2、lemming、Liquor和Car Scale的跟踪结果。该图中不同颜色的矩形框对应于不同算法的跟踪结果，具体请参考图5下方的线型说明，其中红色矩形框对应的是本文算法的跟踪结果。

图5 4组视频序列上的部分跟踪结果

由图5可见，Jogging-2序列种第58帧目标被部分遮挡，此时本文算法可以根据未被遮挡的部分信息进行准确跟踪，第75帧以后目标出遮挡，并在后续形变干扰下下，除本文算法外其余对比算法均丢失了目标；lemming序列中第374帧和452帧目标分别经历了两次遮挡，同时也存在尺度变化的干扰，最后只有本文算法能够对目标稳定跟踪；Liquor序列中目标同样在359帧和769帧时分别经历了两次遮挡，并伴随着尺度变化和旋转等干扰因素，该序列中只有本文算法和KCF算法能够有效应对这些干扰因素；Car Scale序列中从(130～178)帧目标被遮挡并伴随着尺度变化，该序列只有本文算法和DSST算法能够准确定位目标同时适应目标尺度的变化。

综上所述，定性实验进一步验证了本文算法在应对遮挡、尺度变化以及目标形变等多种干扰因素时具有较好的准确性和鲁棒性。

4 结语

本文提出一种尺度自适应的分块核相关滤波目标跟踪算法，当目标被遮挡时可以利用未被遮挡的目标子块提供的位置信息对目标进行准确定位，为了进一步提升算法的性能，引入了融合特征HOG-CN.此外，还提出一种利用目标子块间相对位置的变化情况计算目标尺度的方法。实验结果表明，本文算法在综合性能测试以及在不同干扰因素下的测试都有非常出色的表现，特别是在应对目标遮挡、尺度变化以及目标形变等情况时的性能有显著提升。