不同斜槽情况下感应电机齿部电磁力分布特点

王 山，刘 冉，李 航，王梓旭

（1.德州恒力电机有限责任公司，山东 德州 253005；2.华北电力大学 电气与电子工程学院，北京 102206）

0 引 言

随着人们对环境噪声污染治理和舰船辅机等隐蔽设施的隐蔽性能要求的提高，研制以电机为首的低振动低噪声驱动设备至关重要。电机主要噪声源有电磁噪声、机械噪声以及通风噪声，其中电磁噪声是由电机气隙中磁场相互作用产生随时间和空间变化的径向力使定子铁心和机座发生振动而引发[1]。通过合理的槽配合和斜槽方法能够有效抑制电机径向电磁力，达到降低电机电磁噪声的目的。电机的斜槽设计由来已久，文献[2]对比了斜槽情况下电机电磁振动的变化情况，通过电磁振动的时域和频域分析，选取机壳的特定点测试振动情况，最终发现转子斜槽设计能有效减小振动位移的波动。文献[3]推导了一种新型斜槽转子的径向激振力波公式，并对比了单斜槽、双斜槽以及新型斜槽转子电机的振动加速度，分析新斜槽结构电机的转矩与损耗，验证了其设计的可行性，结果表明该新型斜槽结构能有效抑制特定频率下的振动加速度。斜槽转子设计与不同槽配合的组合能够有效抑制电磁振动，文献[4]基于二维傅里叶分解方法获得较为准确的电机径向电磁力波时空变化特性，通过对比4种槽配合和斜槽设计方案，寻找最优的振动噪声组合。与此同时，针对斜槽率变化对电机振动影响的研究，尤其是不同斜槽率的齿部集中受力变化规律研究不多。

本文以一台11 kW-4极感应电机为例，从气隙磁密入手，基于Maxwell应力张量模型获得径向激振力波和切向激振力波，通过径向激振力波的齿部积分研究定子齿边沿受力分布规律，同时探究了感应电机转子斜槽优化方案对齿部所受激振力的抑制程度。

1 径向和切向磁密计算

转子导条切割磁感线会产生一系列旋转磁动势，其中气隙总磁动势为

p次基波磁动势为

定子v次谐波磁动势为

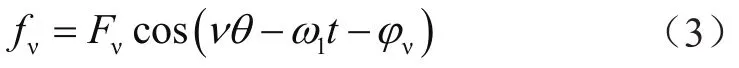
转子μ次谐波磁动势

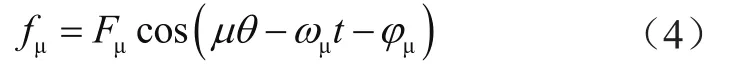
式中：ω1为电源角频率；为转子谐波磁势相对于定子的角频率；为各磁势初相角。定转子开槽产生各阶磁导谐波，总气隙磁导表达式为

定子槽磁导为

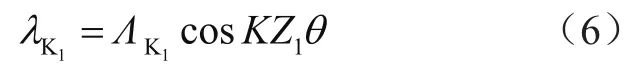
转子槽磁导为

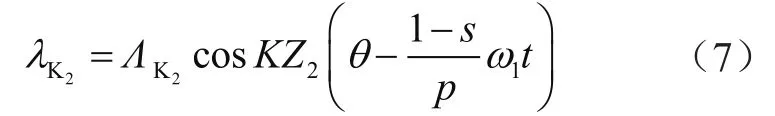
定转子均开槽的相互作用磁导为

式中：λ0为磁导恒定值，Z1、Z2为定转子开槽数；Λ为磁导幅值；s为转差率；K为磁导谐波阶数。计及定转子谐波磁势和磁导谐波的气隙磁密的解析表达式为

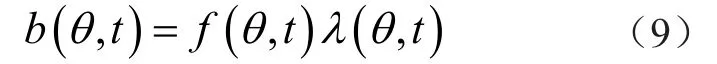
将磁密分解为径向分量和切向分量，计算公式为

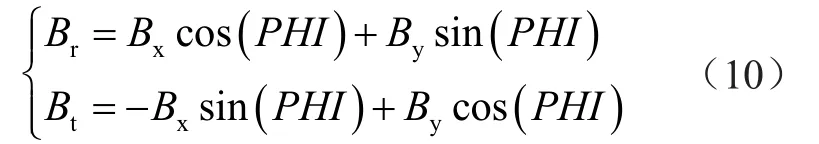
以此为基础，计算径向激振力和切向激振力。

2 计及斜槽时的电磁激振力计算

2.1 激振力波及齿部集中力计算

气隙磁场可视为定子磁场和转子磁场叠加，其表达式为

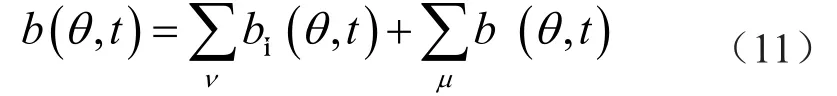
代入应力方程，可以得到径向激振力为

由式（12）可知，径向激振力主要由5种不同性质的叠加磁场组合而成，分别是定子基波和谐波磁场、转子谐波磁场、定子不同次谐波磁场、转子不同次谐波磁场以及定转子磁场。其中，定转子磁场力波次数较少，是径向激振力的主要构成。径向磁密的表达式为

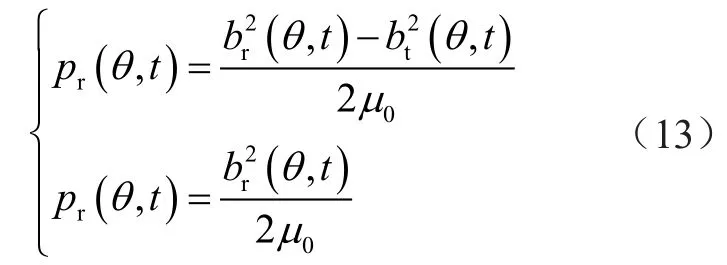
切向磁密的表达式为

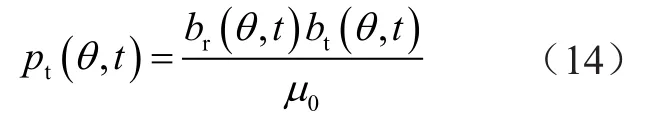
式中：μ0为真空磁导常数。

选取完整的定子齿，齿部集中受力变化由激振力波在齿部区域的体积分求得，即

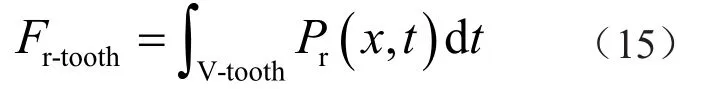
2.2 斜槽时的电磁激振力

电机斜槽或斜极设计的本质是通过合理的机械错位实现齿槽间磁密相移，从而使径向力波沿电机长度方向的轴线发生相位移，在一定程度上削减了轴向的平均径向力，从而抑制振动噪声[5]。

斜槽相对直槽设计也有一定的弊端，磁密相位的不均等会产生槽间横向电流，而横向电流会产生轴向力、附加损耗以及附加转矩。斜槽修正引起的横向电流如图1所示。

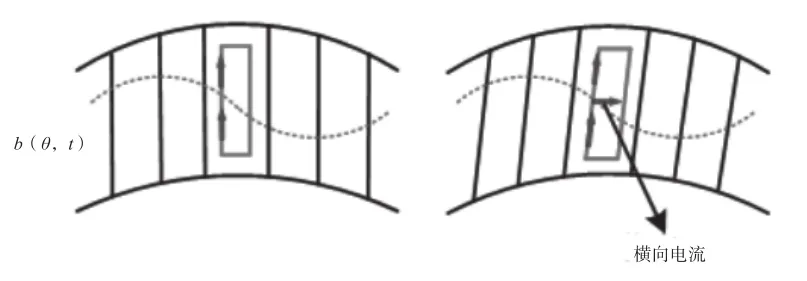
图1 斜槽修正引起的横向电流

考虑转子斜槽造成的谐波磁场轴向偏移，增加转子谐波磁场相位的附加分量。当定子直槽、转子斜槽时，v次定子谐波磁场为

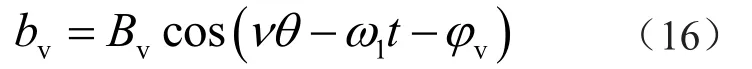
对应转子μ次谐波磁场为

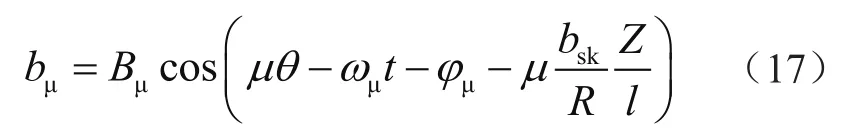
式中：bsk为斜槽距；R为转子外径；l为转子铁心轴向长度。将式（16）和式（17）带入径向激振力方程，即

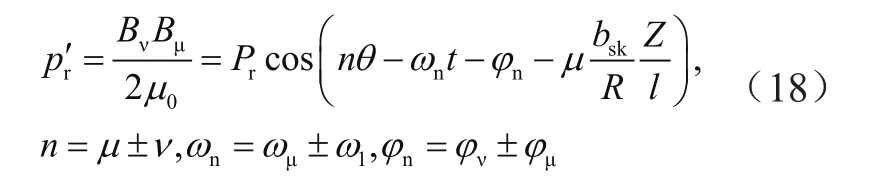
对径向激振力波沿电机轴向长度积分，可以得到斜槽平均径向力为

式中：ksk为斜槽系数。从式（19）可以看出，斜槽造成的轴向径向力与斜槽系数呈正比例关系。

3 仿真结果分析

3.1 计及斜槽时的电磁力

以一台小容量感应电机为例，计算并分析正弦供电情况下的气隙磁密、电磁激振力波及定子齿集中力。感应电机的基本参数如表1所示。

表1 感应电机基本参数

计算径向磁密和切向磁密，结果如图2所示。

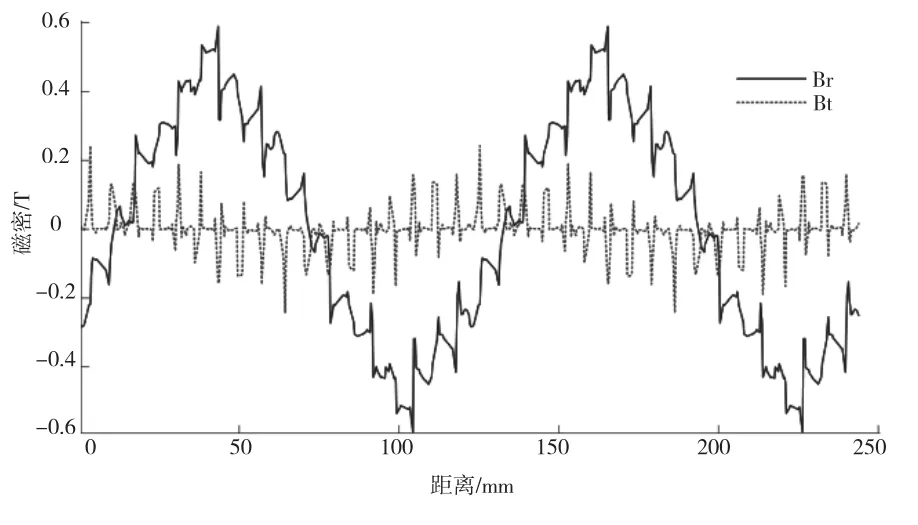
图2 径向磁密和切向磁密

该方法求得径向磁密有效值为1.180 2 T，切向磁密有效值为0.485 7 T。相对径向磁密，切向磁密占比较小。计算径向激振力波，依据是否忽略切向磁密得到径向激振力波形和近似波形，如图3所示。

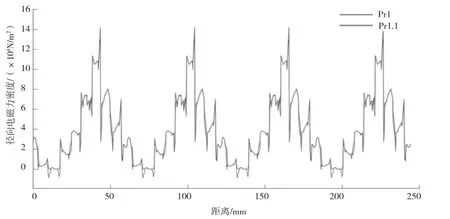
图3 激振力波求解结果

根据式（13）和式（14）计算径向激振力和切向激振力，结果如图4所示。

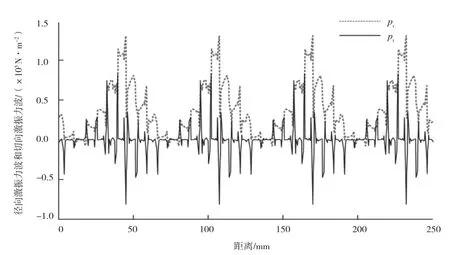
图4 径向激振力和切向激振力结果对比

在电机振动与噪声分析过程中，径向激振力是主要因素，切向激振力是次要因素。感应电机的径向激振力波主要作用于定子齿上，通过力波在定子齿上的体积分能够获得齿部的受力情况。电机模型及选中的积分区域如图5（a）、图5（b）所示。

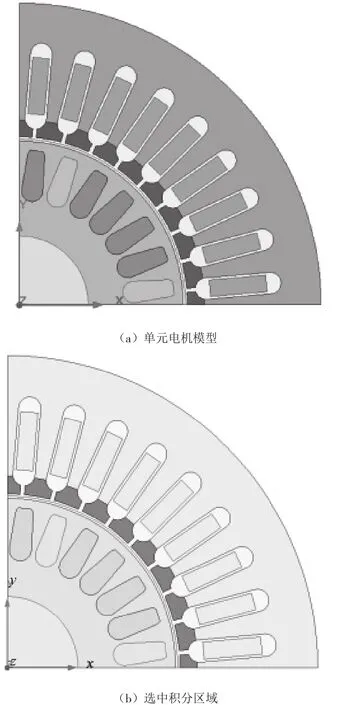
图5 电机模型与径向激振力波积分区域

选取单元电机中的完整定子齿部，计算径向激振力波在电机8个完整的定子齿上的体积分，求得定子齿上的集中力分布如图6所示。

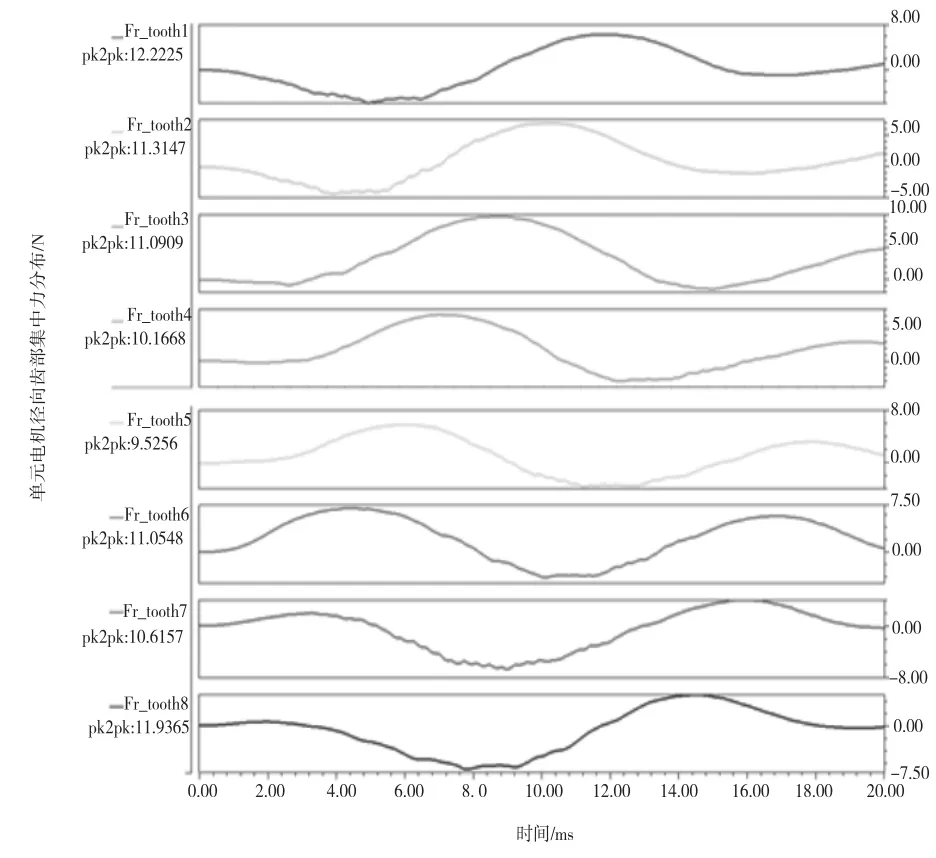
图6 定子齿受力情况

根据1号齿到8号齿位置的激振力峰值分布情况可以看出，相邻齿间的激振力具有较为均匀的相位间隔，激振力的有效值从1号齿位置到8号齿位置先减后增，在5号齿的位置达到最小。

3.2 不同槽斜度下的齿部受力特点

为了获得斜槽设计后定子齿部受力变化情况，设计了斜槽率分别为0.5、0.8、1.0以及1.5的分段斜槽方案，并观察对应齿部受力情况，结果如图7所示。

图7 不同斜槽方案下的齿部受力情况

随着斜槽率的增大，径向齿部集中力幅值逐渐减小，切向齿部集中力逐渐增大。由于径向齿部集中力是影响振动的主要因素，因此适当的斜槽设计能够有效减小激振力幅值。

4 结 论

通过对比感应电机的4种斜槽方案，发现斜槽率较高的方案能有效抑制径向激振力，降低定子齿部受力幅值，在一定程度上抑制电机振动，但同时也会导致齿部切向受力增加，未来将继续对此进行深入研究。