基于GIS信息的城市配电系统网格化动态投资策略探究

2022-02-23丁钰真许浩伟

通信电源技术 2022年24期

冯晗，张伟，丁钰真，许浩伟

（1.国网郑州供电公司，河南郑州 450000；2.国网河南能源互联网电力设计院有限公司，河南郑州 450000）

0 引言

电能作为当前应用范围最广、利用率最高的能源之一，其稳定供应在城市经济发展与建设中发挥着重要的作用。我国电力行业相比于国外，自动化起步较晚，技术条件和经济条件还受到较大的约束与限制，导致国内配电系统自动化水平较低，发展进程比较缓慢。城市配电系统建设不是一蹴而就的，需根据城市经济情况不断拓展和完善。为了保证收益，应采取有效的手段对城市配电系统建设进行合理规划，作出科学的决策。

由于城市配电系统比较复杂，且集中规划计算量比较大，因此采用网格化方式将城市配电系统划分成若干块网格。针对各个网格的实际需求以及情况，包括网格负荷分布、行政属性等，对其进行动态投资规划，实施相应的投资策略。国内城市配电系统网格化动态投资决策的研究起步较晚，相关经验较少，并且现有的理论与技术还不够成熟。虽然近几年城市配电系统网格规划问题受到研究领域重视，相关学者与专家开展了一系列研究，但是现有的决策方法仍然存在一些不足，在实际应用中存在一定的局限性，投资策略的收益较少，无法达到预期的网格化动态投资经济效果，为此提出此次课题研究。

1 城市配电系统网格化动态投资决策方法

1.1 基于GIS信息配电系统网格划分

在制定城市配电系统网格化动态投资决策之前，需要结合实际情况对配电网格进行划分，此次根据城市地理信息系统（Geographic Information System，GIS）信息划分城市配电网格[1]。从高德地图、百度地图等GIS软件上获取城市GIS信息，城市配电网格划分需要结合城市经济和地理情况，在GIS软件上各个地标、建筑物等都表示为一个地理节点。因为性质不同，可以将地理节点GIS信息划分为教育类、餐饮类、旅游景点类、医疗类、政府机构类、住宅类、美容类以及体育健身类等，使用字母编码的方式将获取的GIS信息进行编码，并将编码后的GIS信息标识在城市三维地理模型上[2]。城市配电系统主要是满足用户供电需求，模型上GIS节点的数量越多，供电需求就越大，因此根据模型上GIS节点的密度划分网格，具体情况如图1所示。

图1中划分了A、B、C共3个网格，有明显的GIS节点密度区别。根据GIS信息计算出城市区域配电节点密度，计算公式为

式中：d为城市网格配电节点密度；s为网格GIS节点数量；h为区域GIS节点平均间距；e为区域地理面积；b为城市总GIS节点数量；x为城市总地理面积。

根据实际情况设定阈值，将GIS节点密度大于阈值的区域划分为一级网格，在此基础上设定二级网格配电节点密度阈值，以此划分二级网格。按照该步骤直到城市所有GIS地理节点都被划分到网格内为止，以此完成配电系统网格划分[3]。

1.2 建立投资目标函数

城市配电系统网格化动态投资策略的实施不仅要保证供电的稳定性和安全性，还要保证投资收益，因此在上述基础上以网格投资收益最大、线路损耗最小、配电系统重载率最小为目标建立目标函数。

（1）网格化投资收益最大目标函数。假设城市配电系统的投资规划年限为n，划分的网格数量为m，每个网格的投资项目数量为k[4]。要想保证收益最大，就要将投资成本降到最低。其目标函数表达式为

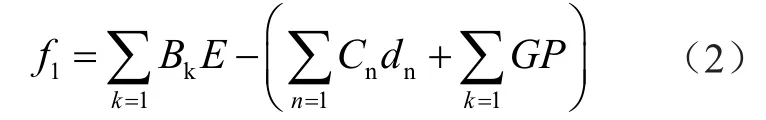
式中：f1为网格化动态投资收益最大值；Bk为网格化动态投资效益折算到第1年的现值；E为投资效益耦合特性矩阵；Cn为网格内配电设施建设成本；dn为第n年配电线路建设长度；G为第n年网格内电源投资成本；P为网格内分布式电源功率值。

（2）线路损耗最小目标函数。根据网格线路损耗功率和线路长度，计算出网格化动态投资策略线路损耗最小的目标函数为

式中：f2为网格化动态投资策略线路损耗最小的目标函数；h为网格配电线路数量；Nn为n年时网格化动态投资配电母线数量；L为网格配电线路损耗功率。

（3）配电系统重载率最小目标函数。根据城市配电系统网格内所有线路的平均重载率，计算出投资策略实施下配电系统的重载率，该目标函数表示为

式中：f3为网格化动态投资策略配电系统重载率最小的目标函数；Wm为城市配电系统第m个网格所有线路的平均重载率[5]。

通过对以上3个目标的整合，建立动态投资多目标函数，其用公式表示为

式中：f表示城市配电系统网格化动态投资策略的多目标函数。

1.3 最优投资策略求解

目标函数有多个解，通过对其约束，求出最优解，将其作为最终网格化动态投资策略。考虑到城市配电系统运行、网架结构，设定约束条件[6]。网格化动态投资策略的实施要满足城市配电系统的运行需求，建立的约束条件为

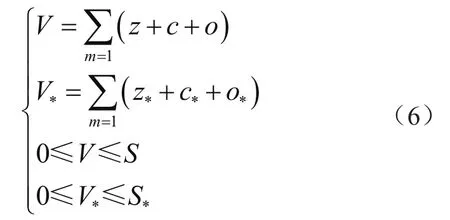
式中：V、V*分别为负荷有功功率总和、无功功率总和；z、z*分别为负荷有功功率、无功功率；c、c*分别为网格有功损耗、无功损耗；o、o*分别为网格内分布式电源有功、无功功率；S、S*分别为负荷有功、无功功率最大值。

城市配电系统还需要满足辐射状运行的网架结构，对其约束为

式中：yij为网格线路连接关系变量；ηij为网格线路节点i到节点j的关系变量；ηji为网格所有可能线路构成的集合[7]。

利用以上2个约束条件对目标函数解约束，求出符合约束条件的最优解，将其作为配电系统网格化动态投资的最优策略。

2 实验论证

为了验证本次提出的城市配电系统网格化动态投资决策思路的可行性与可靠性，选择某城市配电系统作为实验对象。该配电系统目前现有的线路数量为32条，总长为5 643.62 km，配电面积为26 483.64 km²。根据该区域未来8～10年经济发展趋势，需要加大城市配电规模，利用此次设计方法与传统方法对该城市配电系统网格化动态投资进行决策。传统方法分别为基于蚁群算法与基于大数据技术，以下将用传统方法1与传统方法2表示。实验从高德地图、百度地图等GIS软件上获取到该城市GIS信息共1.62 GB，包括26 486个GIS地理节点，利用式（1）划分了3个网格，每个网格的供电节点数量分别为11 648、8 641、6 587，按照式（2）～式（7）得到投资策略，具体如表1所示。

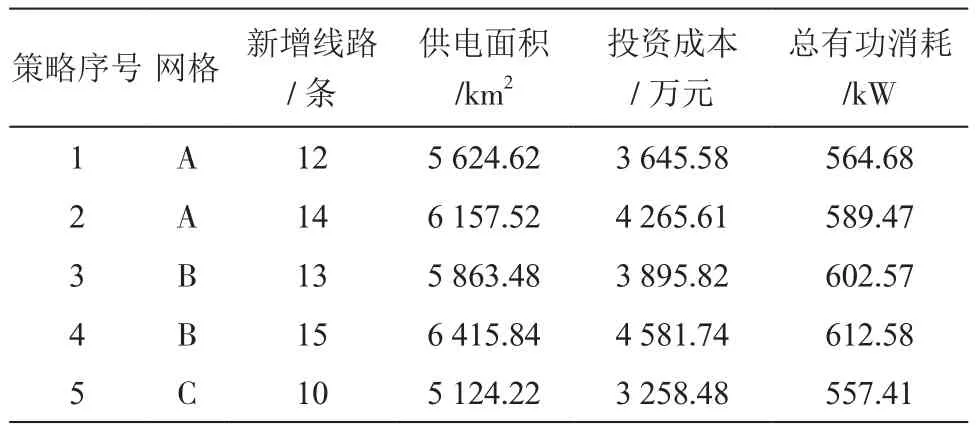
表1 城市配电系统网格化动态投资策略

实验以投资策略实施收益为3种方法评价指标，选取投资策略中的7个项目，利用OIFA软件对投资项目1年内的投资收益进行预测，使用电子表格对实验数据记录，具体数据如表2所示。

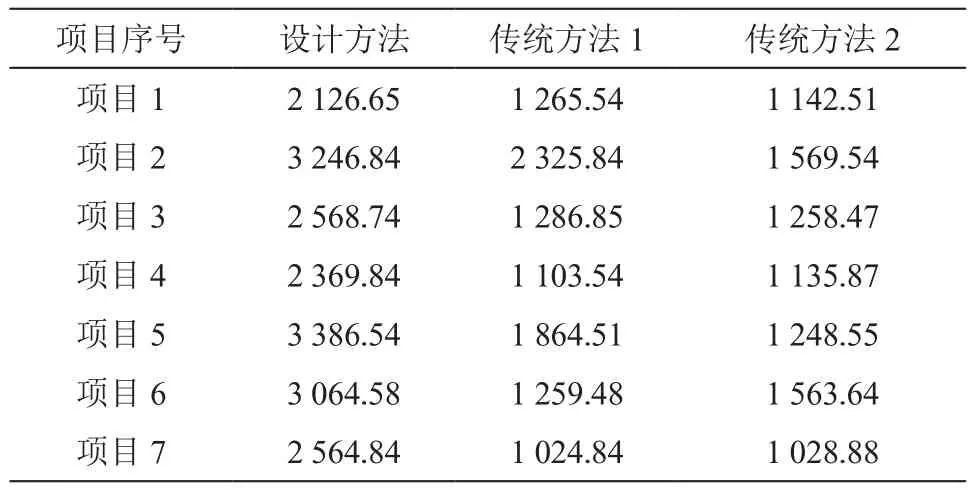
表2 3种方法投资收益对比单位：万元

通过对表2中数据分析，可以得出以下结论。实施设计方法的配电系统网格化动态投资策略所预测的7个项目1年内的投资收益比较高，总收益为19 328.03万元，2种传统方法的总收益分别为8 970.60万元、8 947.46万元，设计方法比2种传统方法收益高出115.46%、116.02%。实验结果证明了根据设计方法作出的城市配电系统网格化动态投资策略具有较好的收益效果，相比较传统方法更适用于城市配电系统网格化动态投资策略分析。