钢框架内嵌角部圆弧缺口AAC砌体填充墙滞回性能研究
2022-02-23郁有升郭亚楠
郁有升,郭亚楠
(青岛理工大学 土木工程学院,山东 青岛 266033)
0 引 言
填充墙框架结构在国内外建筑领域得到了广泛的应用。在传统的结构设计中,由于填充墙通常被视为一种建筑围护结构[1-2],其与框架结构间的相互作用常常被忽略[3]。然而,由2008年中国汶川地震的调查结果及相关研究可知,填充墙的刚度效应及约束效应对框架结构产生了不利的影响[4-5]。针对此问题,有研究者提出了带缺口的填充墙[6-7]。周云等[8]提出了对填充墙进行开缝处理的做法。唐兴荣等[9]对带竖缝的砌体填充墙钢筋混凝土(RC)框架结构进行了低周反复荷载作用下的对比试验。李艳艳等[10]对带缝填充墙RC框架结构进行了抗震性能试验研究,结果表明竖缝的宽度对填充墙框架结构的结构性能有着重要的影响。Jiang等[11]对砌体填充墙RC框架结构进行了试验,结果发现柔性连接降低了框架的强度、刚度和耗能能力,但提高了其延性。Sun等[12-13]对带钢筋混凝土填充墙的部分约束钢框架(PSRCW)进行了试验研究,结果发现带有竖缝的PSRCW具有更大的延性、变形性能和耗能能力。Yuen等[14]对带缝砌体填充墙RC框架进行了振动台试验,结果表明带缝构造可有效减少填充墙和框架之间不利的相互作用。郁有升等[15-16]对带竖缝的压蒸无石棉纤维素纤维水泥平板(CCA)填充墙钢框架结构进行了试验及有限元研究,结果发现带缝构造能有效延缓CCA填充墙的开裂,弱化CCA填充墙对钢框架承载能力及刚度的贡献。
如上所述,近几年来国内外对带缺口填充墙框架的研究主要集中在钢筋混凝土框架上,且缺口形式多为对填充墙的竖向开缝及横向开缝,对角部带圆弧缺口的填充墙钢框架结构(图1,其中,L′、H′分别为AAC砌体填充墙的跨度、高度,l1为圆弧缺口端点到填充墙角部的距离,l2为圆弧缺口中点到填充墙角部的距离)少有研究。基于在填充墙的角部设置缺口可弱化其拉(压)力带的原理,本文利用有限元软件ABAQUS对带圆弧缺口的蒸压轻质加气混凝土(AAC)砌体填充墙钢框架进行模拟分析,研究填充墙设置圆弧缺口构造对钢框架滞回性能、承载能力、延性、刚度退化、强度退化及耗能能力的影响,并确定圆弧缺口尺寸的最优取值范围。

图1 圆弧缺口AAC砌体填充墙钢框架示意图Fig.1 Diagram of AAC Masonry Infill Wall with Circular-arc Openings Embedded in Steel Frame
1 有限元分析
1.1 试件设计
本文共设计了11个试件,钢材均采用Q355钢,各试件的参数如表1所示。各试件的跨度均为4 400 mm,层高为3 000 mm,梁、柱截面尺寸分别为H300×150×6.5×9、H200×200×8×12。KJ-1试件为纯钢框架,KJ-2试件为无缺口的AAC砌体填充墙钢框架,KJ-3试件组为带缺口的AAC砌体填充墙钢框架,墙体厚度均为100 mm。KJ-3试件组的缺口设置在AAC砌体填充墙的4个角部,缺口呈圆弧状,圆弧缺口的弧长S=πl/2(l为圆弧半径);KJ-3试件组包括9个试件,即KJ-3-1~KJ-3-9,参数变量为圆弧缺口端点到填充墙角部的距离l1、圆弧缺口中点到填充墙角部的距离l2,l1=l2=l。各试件的尺寸及构造示意图如图2所示。

图2 各试件尺寸(单位:mm)Fig.2 Dimensions of Specimens (Unit:mm)

表1 试件参数Table 1 Parameters of Specimens
1.2 有限元模型的建立
利用有限元软件ABAQUS[17]建立有限元模型,模型由钢梁、钢柱、加劲肋以及AAC砌体填充墙组成。采用实体单元C3D8R模拟钢梁、钢柱、加劲肋以及AAC砌体填充墙。采用“Tie”模拟钢柱与钢梁、钢柱与加劲肋、钢柱与AAC砌体填充墙的连接,建立钢梁与AAC砌体填充墙的接触关系。为避免填充墙的平面外失稳,限制框架在x方向的位移,即Ux=0。为模拟柱脚的固定连接,对柱脚进行全方位的自由度约束,即Ux=Uy=Uz=0,Rx=Ry=Rz=0,其中Ux、Uy、Uz分别为柱脚在x、y、z方向的平动自由度,Rx、Ry、Rz分别为柱脚在x、y、z方向的转动自由度。耦合与顶梁相对应的柱外侧翼缘各节点沿y方向的自由度,在耦合点处施加沿y方向的低周反复荷载。有限元模型如图3所示。

图3 有限元模型Fig.3 Finite Element Model
钢材的材料参数参照文献[18],弹性模量E为2.06×105MPa,泊松比ν为0.3,应力-应变(σ-ε)曲线采用考虑强化段和下降段的三折线模型,如图4(a)所示。AAC砌体的本构关系采用砌体应力-应变试验所得出的本构关系[19],如图4(b)所示,其中,fm为砌体抗压强度平均值,ε0为砌体的峰值应变。AAC砌体的弹性模量为1 745 MPa,泊松比为0.2。

图4 材料本构关系曲线Fig.4 Material Constitutive Relationship Curves
根据美国AISC抗震规范[20],模型采用位移控制加载。加载过程为:以层间位移角θ为0.225%时的位移为加载位移,循环往复3次;以θ=0.5%时的位移为加载位移,循环往复2次;之后层间位移角每次增加0.5%为一组,每组循环2次;以θ=8%时的位移为加载位移,循环往复2次;之后层间位移角每次增加1%为一组,每组循环2次。层间位移角θ的计算示意图如图5所示,θ=Δ/H,Δ为试件的层间位移,H为试件的层高。

图5 层间位移角θ的计算示意图Fig.5 Calculation Diagram of Inter-story Drift Ratio θ
1.3 模型验证
基于本文的建模方法及文献[21]中KJ-3试件组的数据建立有限元模型,将模拟所得的骨架曲线与文献[21]中KJ-2试件试验所得的骨架曲线进行对比,如图6所示。

图6 试验与有限元模拟的骨架曲线对比Fig.6 Comparison of Skeleton Curves Between Test and Finite Element Simulation
从图6可以看出,有限元模拟结果与试验结果基本一致。由于有限元模拟过程中对柱脚滑移和平面外位移的限制较好,有限元模拟得到的峰值荷载略高于试验所得的峰值荷载,说明有限元分析方法的正确性得到了验证。
2 有限元结果分析
2.1 破坏特征
对于试件KJ-1,当θ<1.5%时,试件处于弹性阶段;当θ=10%左右时,4个钢框架梁柱节点域变形严重;当θ=12%左右时,非加载端的上部梁柱节点附近的钢梁下翼缘出现屈曲,随后钢梁上翼缘也出现屈曲;当θ=20%左右时,非加载端的上部梁柱节点附近的钢梁上下翼缘屈曲严重,加载结束,如图7(a)所示。
通过对10个AAC砌体填充墙钢框架试件(KJ-2、KJ-3-1~KJ-3-9)进行有限元分析可知,各试件的破坏模式相似,破坏过程可分为3个阶段,即恒定摩擦阶段、剪切摩擦阶段、塑性破坏阶段。在恒定摩擦阶段,对于KJ-2试件,AAC砌体填充墙的4个角部与钢框架梁柱节点区域产生摩擦,填充墙角部的应力增大;对于KJ-3-1~KJ-3-9试件,由于AAC砌体填充墙4个角部与钢框架梁柱节点附近存在初始缺口,因此AAC砌体填充墙与钢框架梁柱节点区域无接触,填充墙通过AAC砌体间的摩擦承担较小横向荷载。在剪切摩擦阶段,钢框架对AAC砌体填充墙产生了约束作用,AAC砌体填充墙上产生了沿对角线方向的拉(压)力带,AAC砌体填充墙对钢框架承载能力的贡献逐渐增大。在塑性破坏阶段,AAC砌体填充墙对钢框架承载能力的贡献减小,AAC砌体填充墙因破坏严重而逐渐退出工作。KJ-2试件在θ=5%时的荷载低于其极限荷载的85%,说明θ=5%时试件破坏,如图7(b)、(c)所示,AAC砌体填充墙4个角部出现明显应力集中,鼓曲现象明显。KJ-3试件组以KJ-3-5试件为例,图7(d)、(e)展示了试件在θ=5.5%时的应力云图,角部圆弧缺口的存在削弱了试件破坏时AAC砌体填充墙的应力集中现象及鼓曲现象。

图7 各试件破坏时的应力云图Fig.7 Stress Nephogram of Specimens when Failure
2.2 滞回曲线
图8为各试件的侧向荷载-位移滞回曲线。从图8可以看出,各试件均具有饱满的滞回曲线,表明各试件均具有较强的耗能能力。KJ-1、KJ-3-7~KJ-3-9的滞回曲线呈梭形;KJ-2、KJ-3-1~KJ-3-6的滞回曲线由梭形向弓形发展,滞回曲线存在“捏拢”现象,反映了对开裂后AAC砌体填充墙滑移的影响。与KJ-1相比,AAC砌体填充墙钢框架的最大荷载明显增大,表明AAC砌体填充墙的存在显著提高了框架结构的承载能力。与带缺口AAC砌体填充墙钢框架相比,KJ-2的平面内侧移刚度较大,在相同的侧向位移条件下,KJ-2对结构的荷载贡献较大,墙体开裂较早。此外,带缺口AAC砌体填充墙钢框架曲线斜率的下降速率明显小于KJ-2,说明带缺口构造可以有效延缓AAC砌体填充墙钢框架结构的刚度退化速率。

图8 各试件的滞回曲线Fig.8 Hysteresis Curves of Specimens
2.3 骨架曲线及延性
各试件的骨架曲线如图9所示。从图9可以看出,试件KJ-2、KJ-3-1~KJ-3-9的正向极限承载力分别比KJ-1高68.3%、55.2%、56.5%、49.5%、49.0%、47.3%、39.9%、37.4%、27.4%、8.7%,说明AAC砌体填充墙的存在显著提高了钢框架结构的承载能力,而带缺口构造可降低填充墙对框架结构承载力的参与程度。当层间位移角大于4.5%时,KJ-2、KJ-3-1~KJ-3-6的骨架曲线出现下降段,这是由填充墙破坏引起的。延性系数μ可通过公式μ=Δu/Δy(Δu、Δy分别为试件的极限变形和屈服变形)获得,反映了各试件的塑性变形性能。延性系数越大,结构可在强震作用下承受大的塑性变形而不破坏。通过对比可以发现各试件的延性系数μ在8~10,表明各试件具有良好的延性及变形性能。图10给出了屈服荷载Py、屈服位移θy、极限荷载Pu、极限位移θu主要性能点的定义,主要性能点参数数值详见表2。
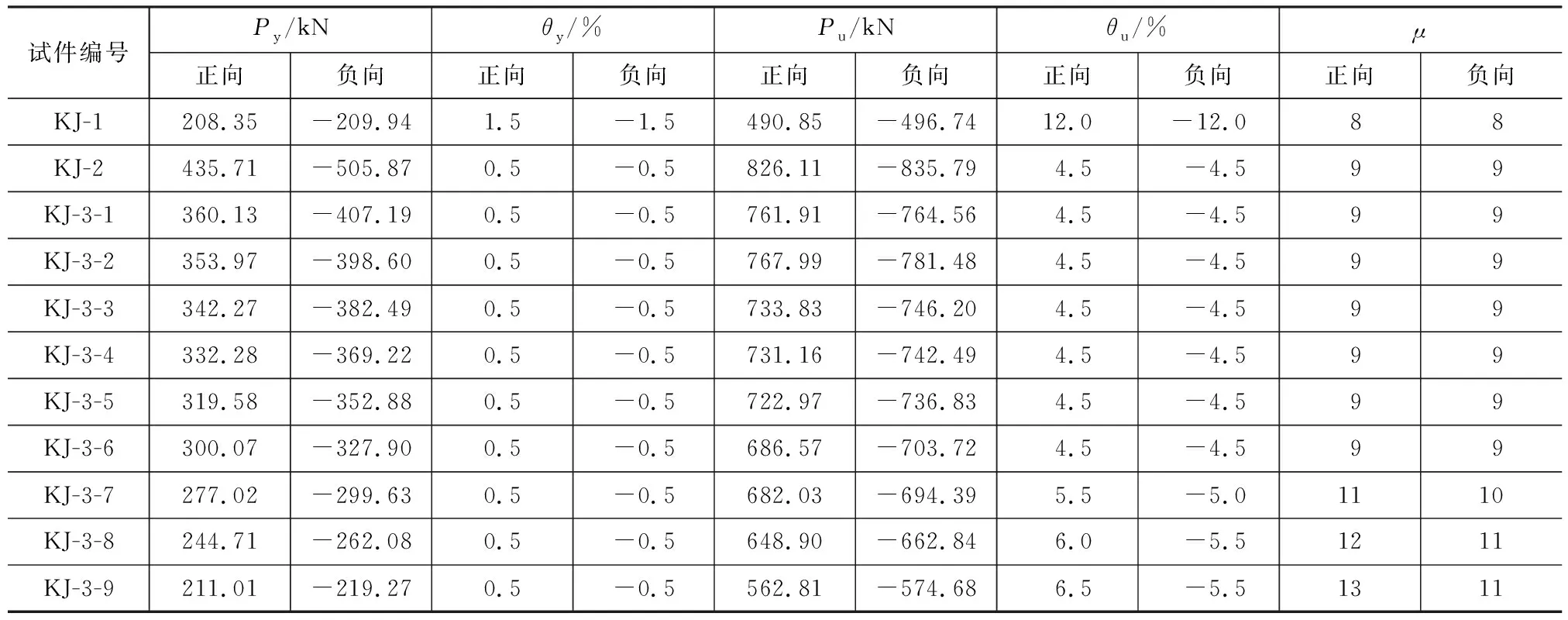
表2 主要性能点参数Table 2 Parameters of Main Performance Points
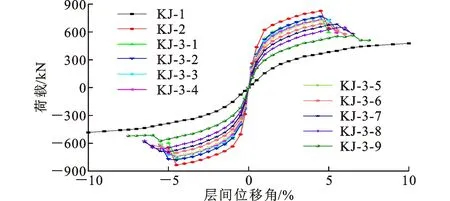
图9 各试件的骨架曲线Fig.9 Skeleton Curves of Specimens

图10 主要性能点的定义Fig.10 Definition of Main Performance Points
2.4 刚度退化
为了分析AAC砌体填充墙对钢框架结构的附加刚度以及带不同尺寸圆弧缺口的AAC砌体填充墙对填充墙钢框架结构的附加刚度,获得低周反复荷载作用下试件的刚度退化规律,对j加载级下试件的刚度Kj进行了对比分析,刚度退化表达式如公式(1)所示。
(1)
式中:Pi,j为j加载级下第i个循环峰值处的荷载值;θi,j为j加载级下第i个循环峰值处的位移值;j=1加载级时k=3,j>1加载级时k=2。
表3给出了初始刚度K0、屈服荷载对应的刚度Ky、极限荷载对应的刚度Ku、AAC砌体填充墙钢框架与KJ-1的刚度之比ηm等主要性能参数,其中ηm可按公式(2)计算。

表3 刚度取值Table 3 Stiffness Values
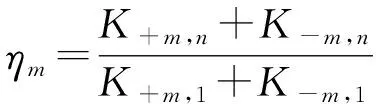
(2)
式中:m=0,y,u;K+m,1、K-m,1分别为试件KJ-1的正向刚度和负向刚度;K+m,n、K-m,n分别为AAC砌体填充墙钢框架试件的正向刚度和负向刚度。
各试件的刚度退化曲线见图11。由于填充墙对钢框架结构的刚度效应,KJ-2、KJ-3-1~KJ-3-9的初始刚度均大于KJ-1,分别为KJ-1的8.12倍、6.61倍、6.46倍、6.20倍、5.97倍、5.68倍、5.25倍、4.76倍、4.12倍和3.22倍。随着层间位移角的增大,试件进入弹塑性阶段,各试件的刚度明显降低。由图11可知,KJ-3-1~KJ-3-9的刚度退化曲线斜率明显小于KJ-2, 说明带缺口构造可以有效延缓AAC砌体填充墙钢框架结构的刚度退化速率。KJ-2、KJ-3-1~KJ-3-9的刚度退化曲线斜率大于KJ-1,原因在于AAC砌体填充墙的开裂及破碎使得其对钢框架的刚度效应减小。当θ<4.5%时,KJ-2、KJ-3-1~KJ-3-6的刚度由AAC砌体填充墙和钢框架共同提供;当θ>4.5%时,其刚度主要由钢框架提供。
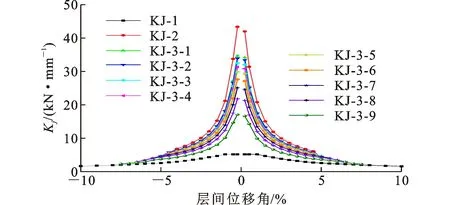
图11 各试件的刚度退化曲线Fig.11 Stiffness Degradation Curves of Specimens
2.5 强度退化
试件的强度退化系数λi可按公式(3)计算。
(3)
式中:Pi-1,j为j加载级下第i-1个循环峰值处的荷载值。
图12为各试件在加载过程中的强度退化系数曲线。研究结果表明,各试件的强度退化系数一般随层间位移角的增大而减小。由图12可知:当层间位移角在-4%~-1%及1%~4%范围内时,各试件的强度退化系数在1.00~1.02之间;当θ>4%时,KJ-2、KJ-3-1~KJ-3-6的强度退化系数明显减小,在0.81~1.01之间,说明KJ-2、KJ-3-1~KJ-3-6的AAC砌体填充墙逐渐被破坏。表4给出了各试件在不同加载阶段强度退化系数的变化范围。从表4可以看出,KJ-1的强度几乎没有退化,强度退化系数在0.99~1.03范围内波动。当AAC砌体填充墙钢框架试件处于弹性阶段(P≤Py)时,KJ-2的强度退化系数大于带缺口AAC砌体填充墙钢框架的强度退化系数;当AAC砌体填充墙钢框架试件处于非弹性阶段(P>Py)时,KJ-2的强度退化系数明显小于带缺口AAC砌体填充墙钢框架的强度退化系数,说明带缺口构造延缓了填充墙钢框架结构的强度退化。
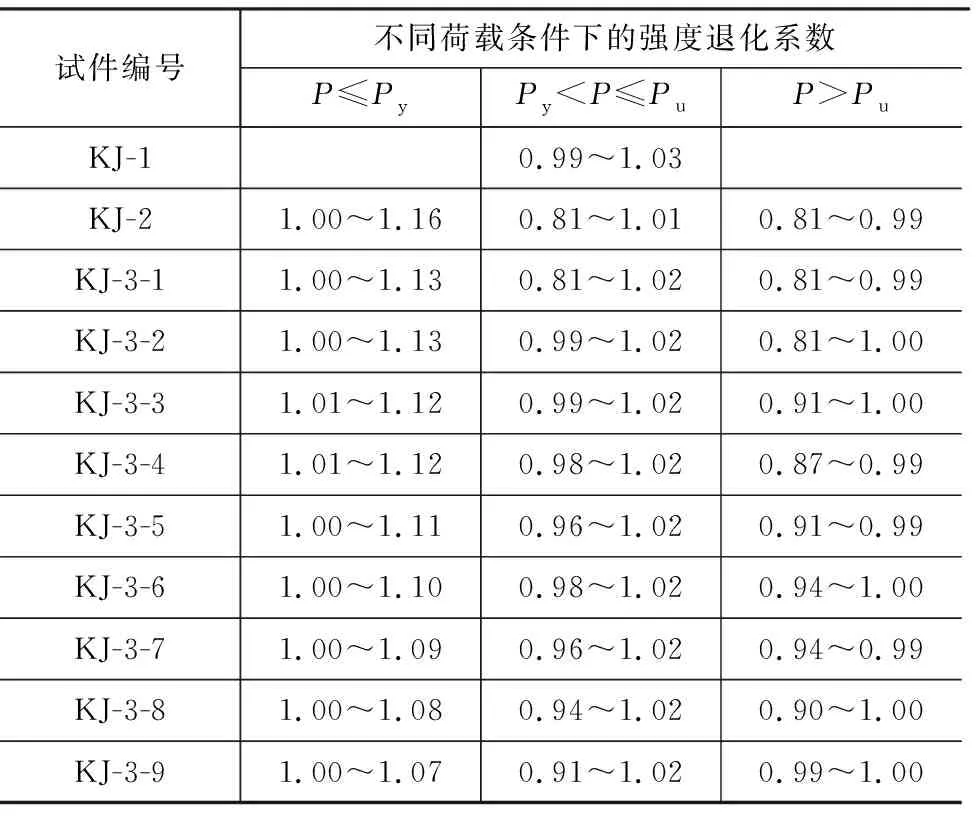
表4 强度退化系数Table 4 Strength Degradation Coefficient
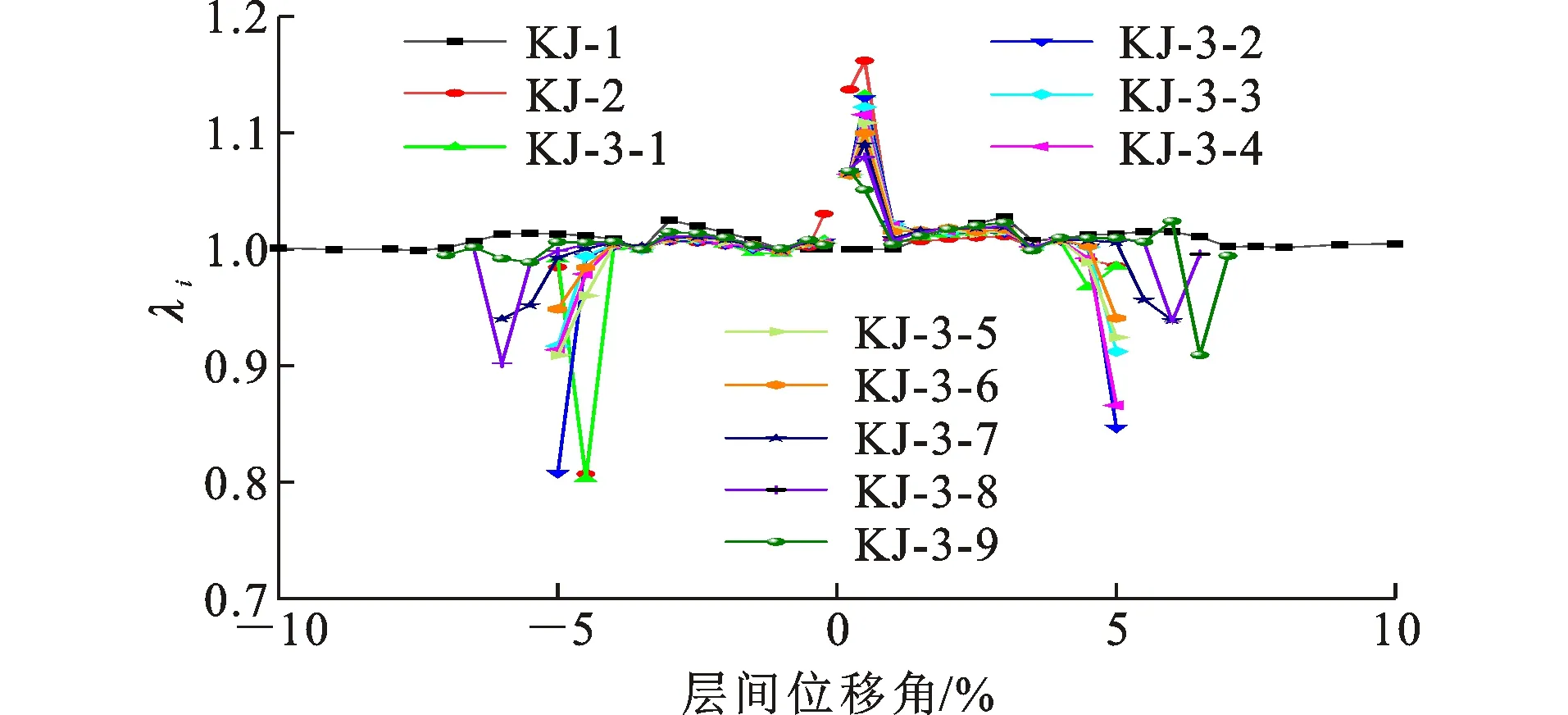
图12 各试件的强度退化系数曲线Fig.12 Strength Degradation Curves of Specimens
2.6 耗能能力
等效黏滞阻尼系数计算示意图如图13所示。根据公式(4)计算等效黏滞阻尼系数he,以此来衡量试件的耗能能力。

图13 等效黏滞阻尼系数计算示意图Fig.13 Calculating Diagram of Equivalent Viscous Damping Coefficient
(4)
式中:SFBE、SFDE分别为一个加载循环中的滞回曲线面积;S△ABO、S△CDO分别为△ABO和△CDO的面积。
图14为各试件的等效黏滞阻尼系数曲线。由图14可知,KJ-1的等效黏滞阻尼系数随层间位移角的增大而逐渐增大。对于AAC砌体填充墙钢框架,当θ<4%时,各试件的等效黏滞阻尼系数均随层间位移角的增大而增大;当θ>4%时,KJ-2、KJ-3-2、KJ-3-3、KJ-3-7的等效黏滞阻尼系数随层间位移角的增大而减小。这表明KJ-2、KJ-3-2、KJ-3-3、KJ-3-7的填充墙因破坏严重而逐渐退出工作。当θ<3%时,AAC砌体填充墙钢框架的耗能能力大于KJ-1的耗能能力;当θ>5%时,AAC砌体填充墙钢框架的耗能能力小于KJ-1的耗能能力。这表明填充墙的存在提高了钢框架结构的耗能能力,但由于填充墙的变形能力差,使得填充墙钢框架先于纯钢框架发生破坏。此外,当θ<3.0%时,KJ-2的等效黏滞阻尼系数增长率明显大于KJ-3-1~KJ-3-9,且KJ-3-1~KJ-3-9的等效黏滞阻尼系数增长率随圆弧缺口的增大而逐渐减小;随着层间位移角的增大,各AAC砌体填充墙钢框架的等效黏滞阻尼系数增长率逐渐减小;当θ在3.0%~4.5%范围内时,各AAC砌体填充墙钢框架的等效黏滞阻尼系数曲线趋于平缓。
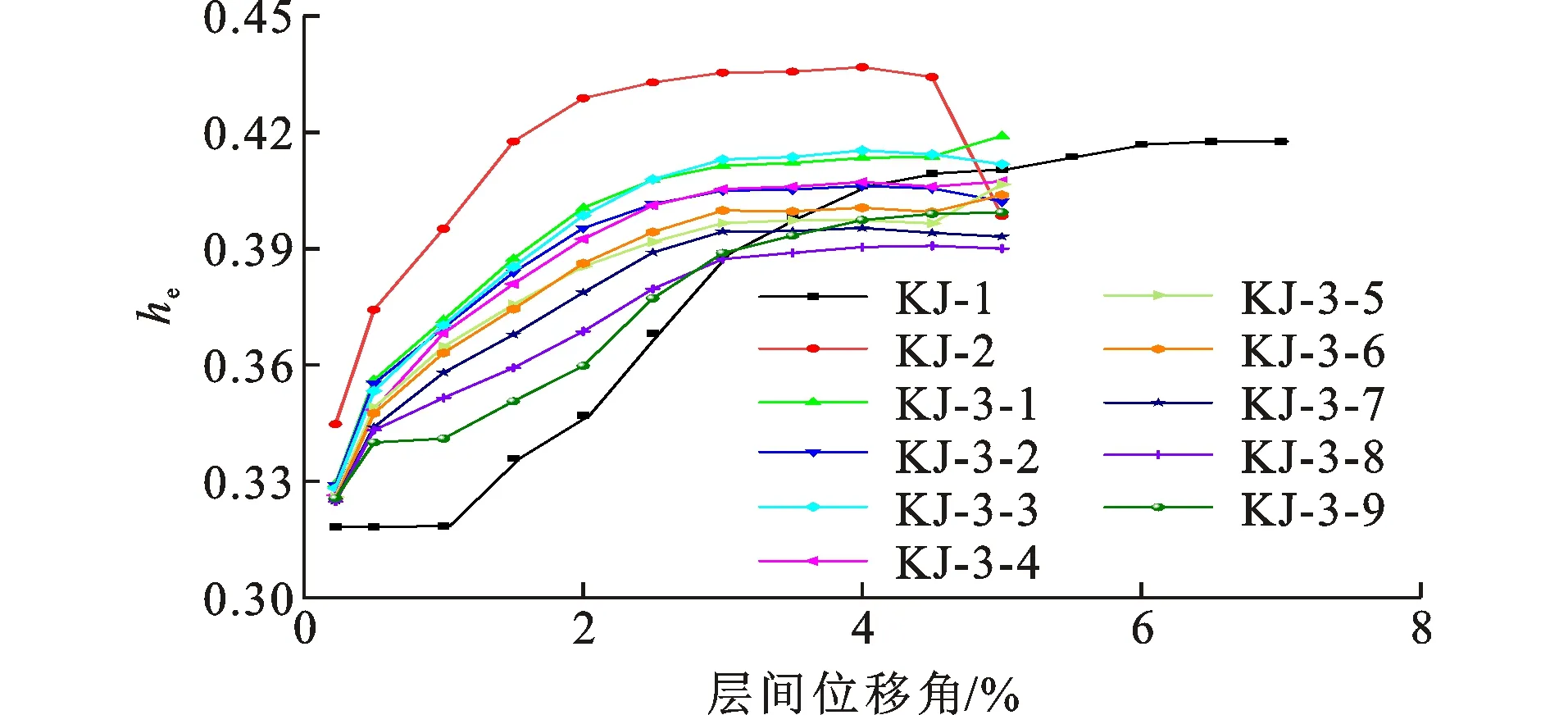
图14 各试件的等效黏滞阻尼系数曲线Fig.14 Equivalent Viscous Damping Coefficient Curves of Specimens
3 结 语
(1)与纯钢框架相比,AAC砌体填充墙钢框架的承载能力、延性、初始刚度和耗能能力均显著提高。
(2)圆弧缺口构造改变了AAC砌体填充墙的破坏模式。对于无缺口AAC砌体填充墙钢框架,填充墙的4个角部与钢框架梁柱节点区域由于接触而产生摩擦,钢框架对填充墙产生较强的约束作用,填充墙上产生了沿对角线方向的拉(压)力带,使得填充墙角部应力集中,最终导致填充墙的整体破坏;对于带缺口AAC砌体填充墙钢框架,圆弧缺口构造减弱了钢框架对填充墙的约束作用,弱化了填充墙的拉(压)力带效应,延缓了墙体的破坏。
(3)圆弧缺口构造可以削弱AAC砌体填充墙对钢框架承载能力和刚度的贡献,同时延缓AAC砌体填充墙钢框架的刚度退化速率。当圆弧缺口过小时,即l
