计及风电不确定性和风速相关性的微网孤岛多目标潮流优化

李红，栗文义

（1.乌海职业技术学院，内蒙古 乌海 016000；2.内蒙古工业大学，内蒙古 呼和浩特 010000）

0 引言

随着微网技术的发展，分布式电源（Distributed Generation，DG）的应用逐渐发展成熟，在电网渗透率逐年升高，风电消纳成为了电网运行中的关键点[1]。以风电为代表的DG不仅能够提高电网调度的灵活性，而且还可以在一定程度上起到潮流优化的作用，从而优化微网运行[2]。

为了获得微网的最佳运行策略，目前主要选用确定性和概率方法。概率方法能够处理含有随机变量的系统，从而得到具有统计意义的输出变量。在电力系统中，负荷、风机出力、光伏出力等常见变量随时间和季节发生变化。在这类问题的求解中，点估计法（Point Estimate Method，PEM）[3]具有较高的应用价值，其计算难度小、得到的解更准确。考虑到随机变量之间的相关性，PEM仍不失为一种优选方法。

针对含风电的潮流优化，文献[4]研究了计及风电不确定性的含UPFC电力系统的两阶段最优潮流。文献[5]研究了基于无迹变换随机潮流建模的主动配电网优化调度。文献[6]研究了计及极端扰动的孤岛微电网潮流优化控制方案。文献[7]利用区间模型考虑风电的不确定性。文献[8]研究了计及电压稳定约束的微电网动态最优潮流。文献[9]研究了基于概率潮流的主动配电网供需群体协同优化运行策略。可见，较多文献均考虑了风电的不确定性，但是对于风电场相关性对微网孤岛运行的影响研究仍不充分。

本文考虑风电场之间的相关性，同时基于下垂控制的DG，考虑下垂参数影响DG的运行点进而影响其调度[10]，因此下垂参数可以作为不确定性风机控制的主要优势。分析了风机出力的不确定性和风速相关性，建立了多目标优化模型，从成本、环保和运行可靠性方面进行优化。考虑到风电和光伏的不确定性，利用PEM进行概率模拟，通过蚁狮算法进行求解。

1 风电不确定性和风电场相关性

1.1 风机出力不确定性

风速的不确定性利用威布尔函数[11]计算：

式中：Pri为风机i的额定功率；vr，vcin，vcout分别为额定风速、切入风速、切出风速。

1.2 风电场相关性

处于相邻区域的多个风电场，由于受到气候条件等因素的影响，彼此风电出力之间往往呈现出一定程度的相关性。一般利用Copula函数模型来考虑这种相关性[12]，首先选择Copula函数，得到风速的联合概率分布函数，对相关参数进行极大似然估计，生成N组Copula随机数向量，再利用Weibull分布变换得到具有相关性的风速序列，便可计算风电的具体出力。

本文考虑风电的下垂参数di，其表达式为

2 微网孤岛多目标优化模型

本文在建立多目标函数中，风电作为DG的一类，其出力Pw也计入到PDG中。

2.1 目标函数

①以电网运行的经济性最大为目标，降低成本费用，包括传统机组成本和DG成本。

2.2 约束条件

（1）等式约束

①功率平衡约束

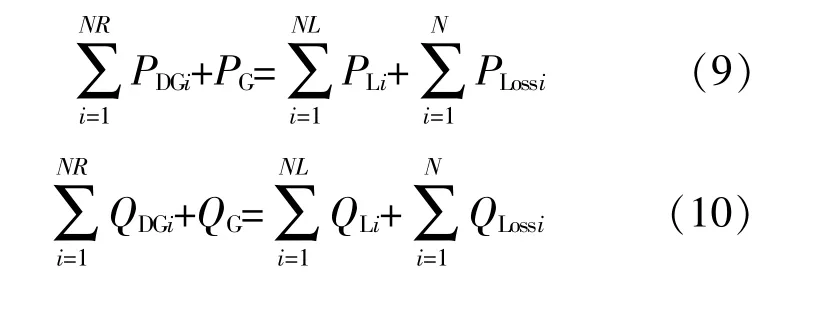
式中：PLi，QLi分别为i节点有功、无功负荷；PLossi，QLossi分别为i节点有功、无功网损；QDGi，QG分别为DG无功出力、传统机组无功出力。

②节点注入有功无功约束

式中：Skmax为线路k的热极限。

3 求解方法

3.1 2PEM+1点估计

2PEM+1点估计适用于处理含有不确定变量的问题，达到估计输出变量的统计特性。考虑一组输出变量H，受一组不确定性输入变量Y的影响，H可表达为

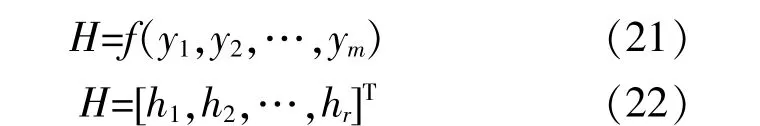
式中：f为将不确定输入变量映射为输出变量的函数；m为随机变量个数。

本文选择2PEM+1点估计计算每个随机变量的位置pl，k和权重wl，k。向量函数f对每一对随机变量进行估计，使得其他变量保持在均值附近，具体表达式为

3.2 Nataf变换

上述2PEM+1点估计未考虑变量之间的相关性，本文考虑采用Nataf变换[13]。根据该变换，随机变量从任意相关分布映射到不相关标准空间。假设任一随机变量集合V和相应的累积分布函数Di（vi）和相关矩阵Cv，根据Nataf变换，通过下式进行相关变量的边缘变换：

得到上述相关性表达式后，利用Cholesky解耦得到标准正交空间的元素位置，将该位置映射到原始任一空间，根据本文的模型进行潮流计算，其中利用点估计进行概率模拟。

3.3 多目标蚁狮算法求解

本文利用多目标蚁狮算法（Multi-objective Antlion Optimization，MALO）进行最优潮流求解。蚁狮优化算法（Antlion Optimization，ALO）模拟了蚁狮的觅食行为，是一种启发式算法[14]。该算法的求解流程图如图1所示。

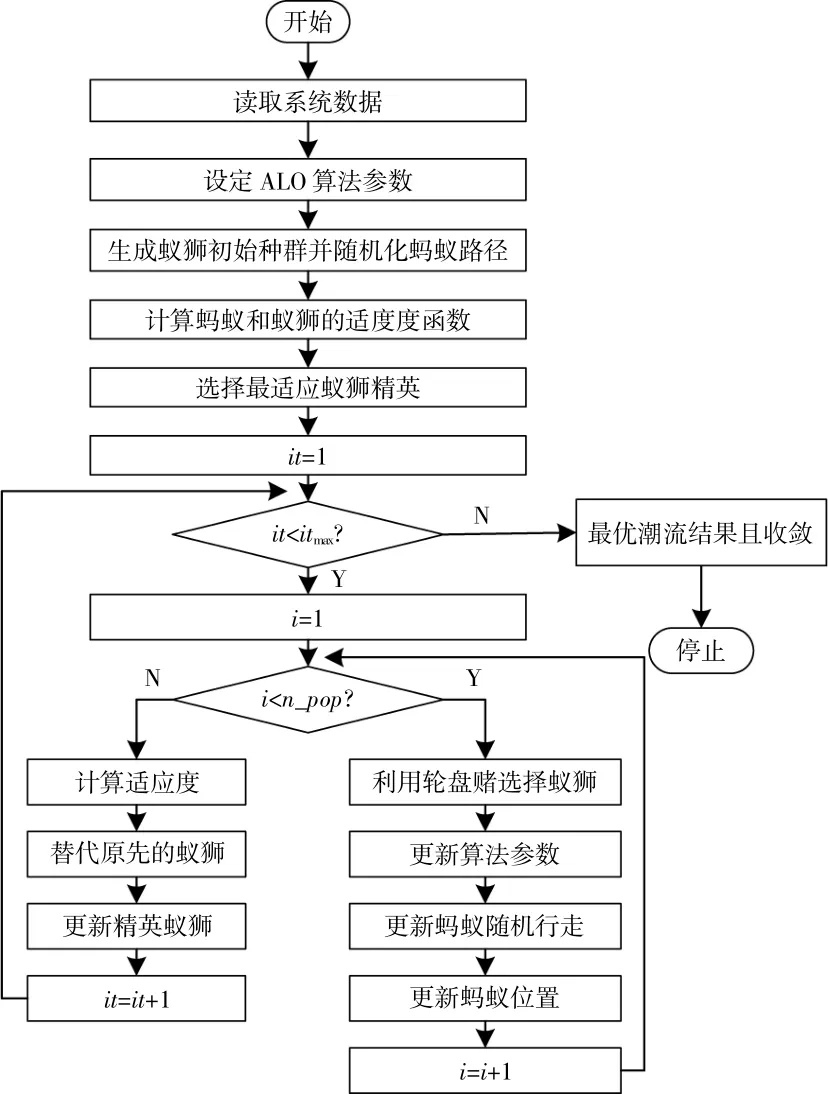
图1 算法流程图Fig.1 Flow chart of the proposed algorithm

本文考虑多目标模型，将ALO扩展为MALO进行求解，本文的求解步骤如下：

①输入系统数据、负荷数据、DG数据、负荷和风电的概率信息，同时初始化算法参数；

②根据随机变量的概率密度函数成对计算变量的位置和权重；

③计算初始值条件下的蚂蚁的适应度，根据2PEM+1点估计计算输出变量；

④从所有目标函数中得到均值，将所有非支配解保存，进行精英选择和随机选择；

⑤完成蚁狮在所选择的精英周围的随机行走，根据蚁狮的位置归一化边界条件；

⑥基于优先级更新蚂蚁的位置，并确保蚂蚁均完成随机行走；

⑦将所有更新过的蚂蚁信息进行保存，并寻找非支配解中的个体，基于位置密度进行排序；

⑧检查集合是否已满，是则将排序最大的蚂蚁剔除，否则进行下一步；

⑨从新的解集中选择精英和随机蚁狮，检查收敛性，如果不收敛进行步骤⑤；

⑩计算每个解对应目标函数的收敛性，对所有目标函数进行模糊化处理并选择一个具有最大归一值的解。

针对本文的多目标函数，考虑转化为单目标函数，其中f1～f3的权重分别为0.3，0.4，0.3。

4 算例分析

4.1 系统说明

如图2所示，对IEEE 33节点进行改进，用于本文仿真分析[15]，仿真环境为MATLAB2012b。除风电外，本文考虑天然气发电、燃油发电和生物质能发电3种形式的DG。相关发电和排放数据见文献[15]。

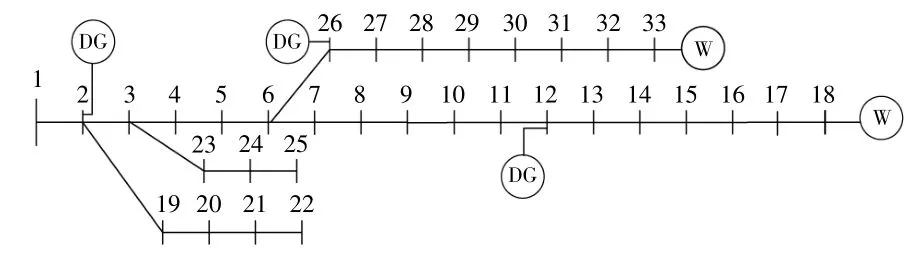
图2 IEEE 33节点系统Fig.2 IEEE 33 bus feeder system

另外，本文仅考虑有功负荷的波动，其标幺值为均值，标准差为均值的10%。假设所有功率因数均为0.85滞后，无功功率可进行调整来确保功率因数恒定。风电为Weibull分布，风机节点为18和33，容量分别为500 kW和250 kW，均以0.85滞后的功率因数运行，其切入、额定和切出风速分别为3，12.5 m/s和25 m/s。两者的形状和尺寸因数分别为2.025和9。本文CO2排放因子为224。

本文分两个场景，其中，场景1不含相关性，场景2含有相关性。

4.2 算例分析

（1）不含相关性优化

首先根据本文算法和2PEM+1点估计求解多目标概率潮流，不考虑风电场之间的相关性。同时，将本文所提算法（MALO）与多目标粒子群算法（MOPSO）进行比较，结果如表1所示。

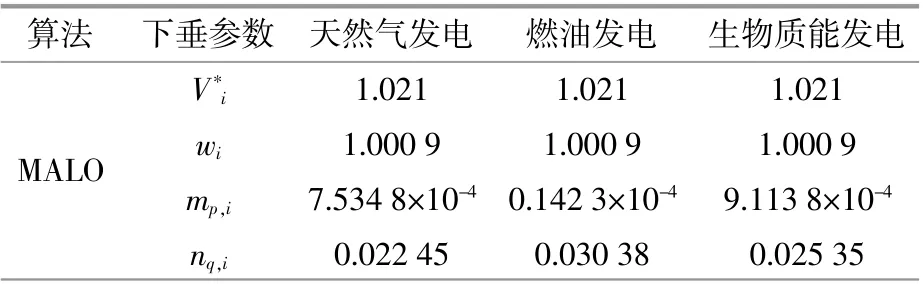
表1 下垂参数对比Table 1 Comparison of droop parameters

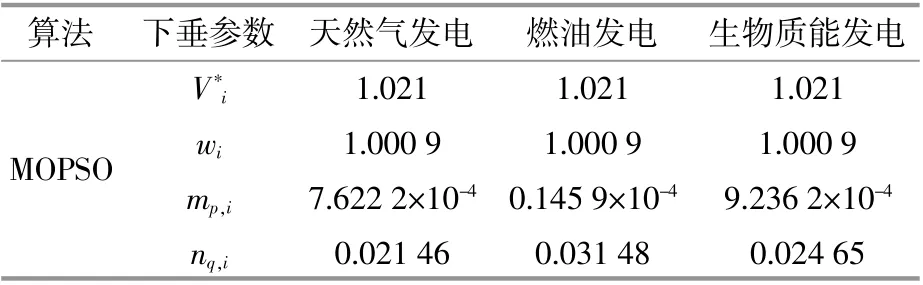
续表1

目标函数的数据如表2，表3和图3所示。同时对比了采用确定性算法和不确定性算法得到的目标函数，可以看出，利用确定性算法得到的目标函数偏小，尤其是电压偏移这一目标函数，这主要是由于优化的下垂参数达到了最大值，所有节点的电压值都接近该优化结果。因此，所有节点的电压偏移都较小，没有出现严重的偏移现象。

表2 不同算法下目标函数值Table 2 Objective values by various algorithms

表3 不同方法下目标函数值Table 3 Objective values by various methods

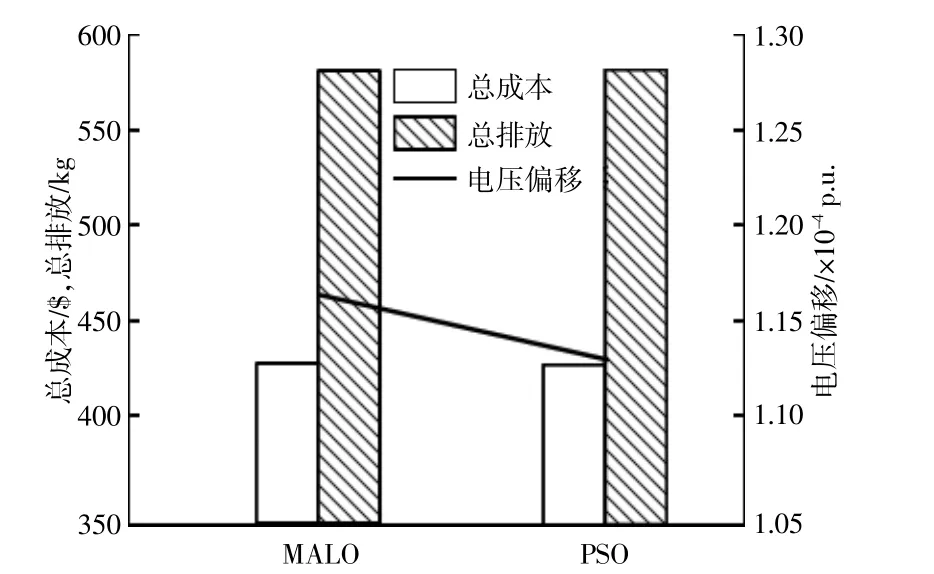
图3 目标函数值对比Fig.3 Objectives by comparison

（2）考虑风电场相关性运行优化

考虑微网孤岛运行时含有风电场相关性的最优潮流。利用Nataf变换，目标函数均值和标准差为0.1～0.9。同时将目标函数值归一化处理。相应的目标函数均值和标准差如图4，5所示。由图可以看出：由于对频率参数和下垂参数的依赖，总发电成本和总排放的均值和标准差相同；相比另外两个目标函数，电压偏移的变化幅度更大。因此，考虑风电场相关性后，总电压偏移的影响更大。

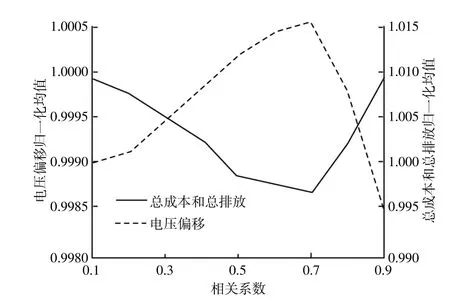
图4 相关系数对均值的影响Fig.4 Impact of correlation on the mean value

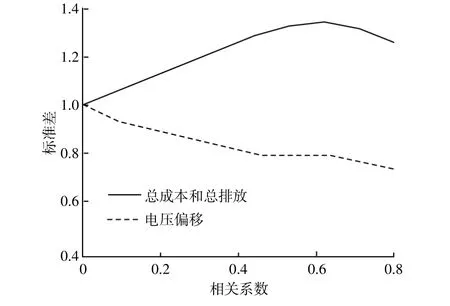
图5 相关系数对标准差的影响Fig.5 Impact of correlation on the standard deviation

5 结论

本文提出了一种考虑风电不确定性和风电场相关性的微网孤岛多目标运行优化模型。利用2PEM+1点估计模拟负荷和风速的不确定性。选择蚁狮算法求解模型的下垂参数，并在IEEE 33节点中进行仿真。仿真结果表明，利用Nataf变换法进行风电相关性分析是有效的，该相关性可以影响风电出力以及其他机组出力，体现在总发电成本和总排放的均值和标准差相同，考虑风电相关性后总电压偏移更大。这是由于风电场相关性导致出力的可调节量相比不考虑相关性有所下降，因此电压偏移会有所提高。算例还说明了本文算法的有效性。