可再生能源交直流送出型电网暂态能量有限时间控制模型

刘宏扬，赵树野，张昭，康赫然，党伟，顾大可，王松阳

（1.国网内蒙古东部电力有限公司经济技术研究院，内蒙古 呼和浩特 010020；2.东北电力大学，吉林 吉林 132012；3.沈阳工业大学，辽宁 沈阳 110870）

0 引言

随着特高压交直流远距离输电通道不断建设和完善，我国电网中经交直流混合通道输送的风电、光伏等可再生能源发电与传统水电、火电容量比例不断提升。风电、光伏发电比例在交直流通道输送容量占比提高的同时，交直流混合输送的安全稳定问题已成为制约交直流混联电网安全稳定的重要因素之一[1]～[4]。在交直流混合送出型的送端电网中，当输送通道、受端电网和送端电网内部发生暂态过程时，提高送端电网乃至整个互联电网的暂态稳定性，是交直流混合送端电网暂态能量控制亟待解决的问题[5]～[8]。

国内外研究人员针对交直流混合送出的送端电网暂态过程能量控制方法开展了较多研究。文献[9]考虑多端柔性直流输电接入电网后对整个网架结构和调节特性带来的影响，提出了含多端柔性直流输电的交直流混联电力系统暂态控制方法。文献[10]考虑风电外送时的强波动性，提出了基于协作式、分布式模型预测的交直流送端电网频率控制方法。文献[11]考虑功角失稳和暂态过电压并存，提出了交直流弱送端暂态控制模型。文献[12]为提高交直流混合外送系统暂态稳定性，提出了考虑系统故障响应轨迹交直流混联外送系统暂态能力计算模型。为提高经交直流风电通道互联的系统的暂态稳定性，文献[13]建立了互联系统暂态稳定鲁棒控制模型。上述研究对直流混合送出型送端电网暂态能量控制奠定了一定的研究基础。在含高比例可再生能源交直流混合送出型送端电网暂态能量控制过程中，各类等值同步电源的协调控制问题，实际上是一个不同控制变量在非线性干扰下的控制优化问题。目前，充分利用储能系统的调节灵活性，通过对可再生能源、储能、火电三者进行协调控制来提高电网暂态稳定性的研究尚未见相关文献报道。

本文首先将可再生能源发电系统、储能系统进行虚拟同步等值，建立了交直流混联电网能量函数模型，并在此基础上提出了交直流混联电网拓扑模型；建立了基于二阶多智能体的送端电网暂态能量有限时间干扰观测器和非线性积分滑模控制模型。基于我国北方某地区可再生能源送出型交直流电网网架结构和数据，仿真验证了所提出的方法能够有效应对可再生能源发电系统不确定性带来的能量调节干扰，提高系统暂态稳定性。

1 可再生能源与储能的虚拟同步模型

为建立交直流混联电网能量函数模型及拓扑模型，首先将可再生能源发电系统、储能系统进行虚拟同步等值（图1）。

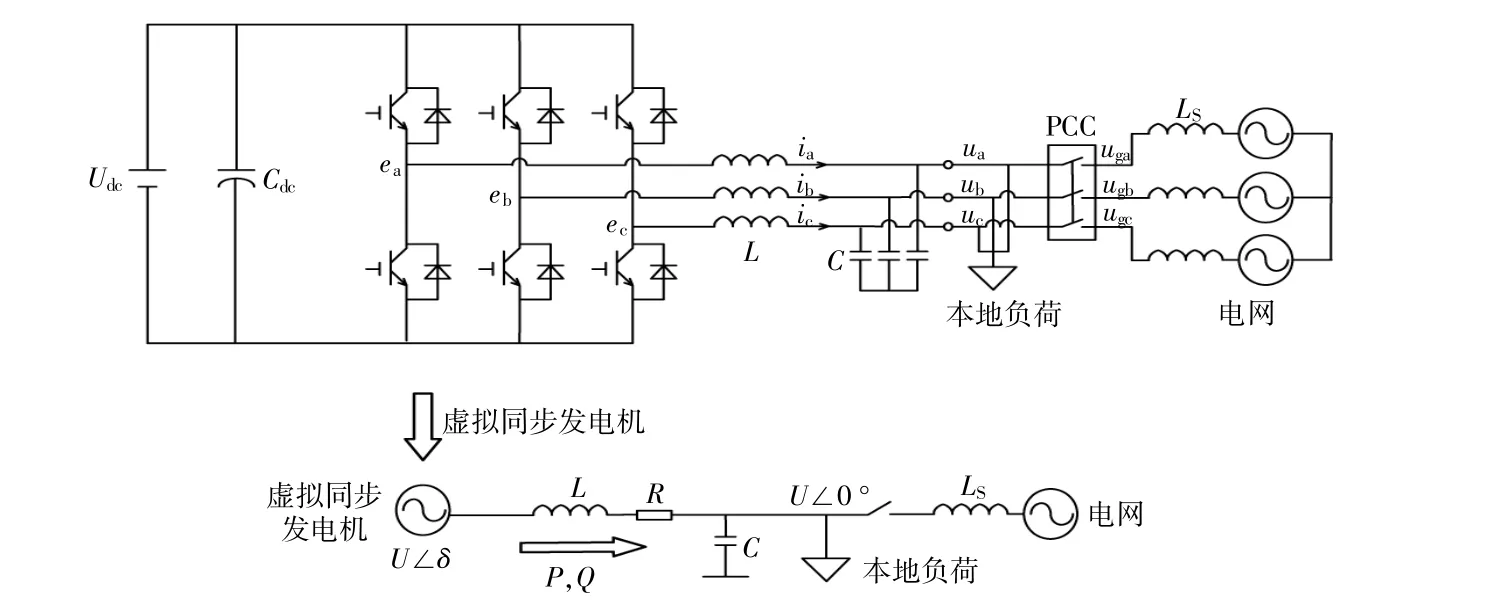
图1 虚拟同步发电机Fig.1 Virtual synchronous generator

对图中虚拟同步发电机的控制模型进行分析，得到[10]：

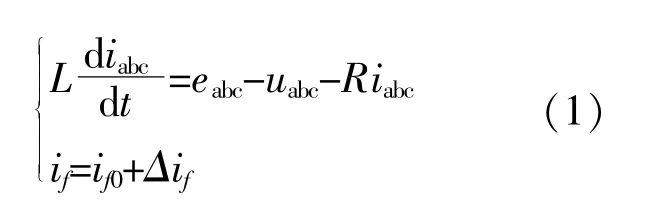
式中：L为同步发电机等效电感；R为同步发电机的等效电阻；eabc为同步发电机的电动势；iabc为同步发电机的机端电流；uabc为同步发电机的机端电压；if0为同步发电机在额定输出功率下的输出励磁电流；Δif为同步发电机电流波动量；if为同步发电机实际输出电流。

推导出虚拟同步发电机的数学模型为

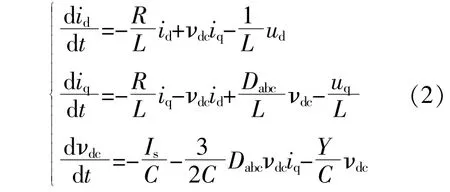
式中：C为同步发电机的等效电容；id，iq分别为dq分量；Dabc为系统的惯量；νdc为虚拟同步等效电路直流部分的电压；Is为输入电流。

2 含可再生能源的交直流混合能量函数模型

考虑可再生能源大规模交直流混合送出的送端系统功角摆动方程为

式中：Di为等值同步电源i的阻尼系数；δi为节点i处的攻角；Mi为惯性时间常数；Pmi，j为第i个等值同步电源输入功率；Pi，z为第i个等值同步电源输出功率分配到直流输送通道上的功率；Pei为各等值同步电源交流输出功率；φij为节点i，j间的相角差。

由式（1）可得交直流互联系统的转子运动方程式：

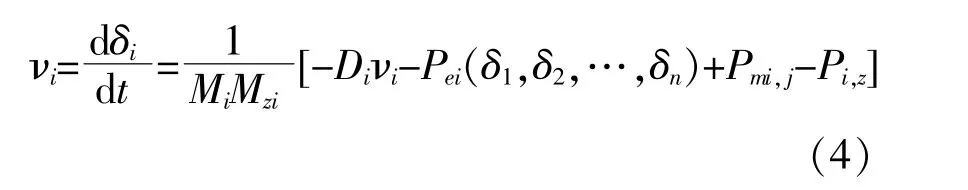
式中：i=1，2，…，α，α+1，…，n，其中的1，2，…，α为火电或水电等同步机组个数，α+1，…，n为将风机、光伏等非同步电源等值后的同步电源个数；Mzi为虚拟惯性时间常数。

交直流混合系统中的能量是由互联系统中各等值发电机的转子所具有的动能和输电系统中积储的势能之和。当忽略系统无功和电压波动时，描述经交直流混合送出型送端电网能量平衡的李雅普诺夫函数为

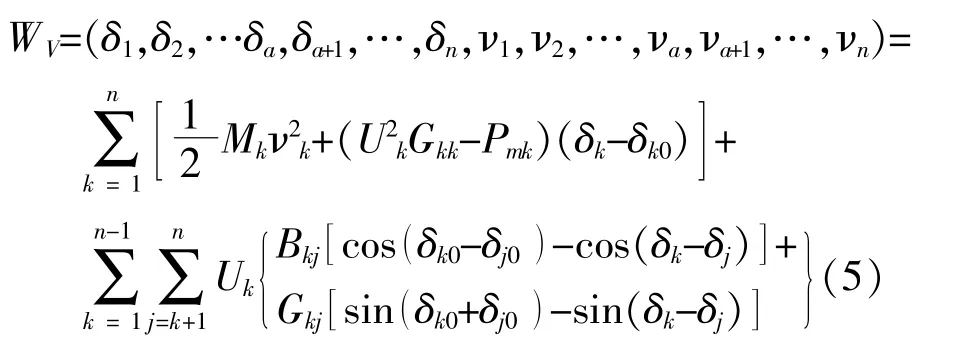
式中：δa+1=f（sa+1），…，δn=（sn）分别为可再生能源发电系统等值为同步电源后的等值功角。

设送端系统中两个等值电源j与k之间的导纳为Yjk=Gjk+jBjk，略去电导部分Gjk（j≠k），有：

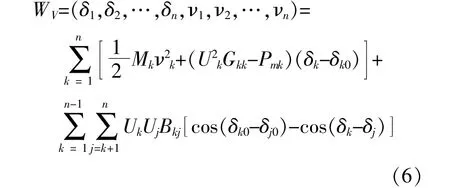
式中：WV（δ1，δ2，…，δn，ν1，ν2，…，vn）为风电、光伏与水电、火电打捆经交直流混联通道送出的送端系统能量平衡临界点处Pei（δ10，δ20，…，δn0）-Pmi=0（i=1，2，…，n）的解，δ10，δ20，…，δn0为各等值同步电源功角临界值。由式（5）和式（6）可以看出有共同的李雅普诺夫函数WV（δ1，δ2，…，δn，ν1，ν2，…，vn），交直流混合送出的送端系统李雅普诺夫函数对时间的导数W·V≤0。因此，交直流混合送出的送端系统是渐近稳定的。

3 二阶多智能体系统的有限时间包容控制

3.1 考虑可再生能源不确定性的暂态功角有限时间控制

在交直流混联电力系统中，通过对储能、可再生能源、同步机组三者的协调控制，能够有效地提高系统暂态稳定性。本文针对系统暂态过程的频率和功角稳定性，预先设置了n′个同步机组主功率调节电源、m′个可再生能源发电系统等值电源和k′个储能设备。其中，每个功率调节电源均对应于交直流混联电网拓扑结构G中的一个节点，各节点间的功率交换大小即为交直流混联电网拓扑结构G的边。在不考虑交直流混联电网暂态过程中，可再生能源电源出力不确定性干扰时的交直流混联电力系统暂态过程动力学模型为

式中：i={1，2，…，n′，n′+1，…，，n′+m′+k′}，n′为主调节电源个数，m′为新能源调节电源个数，k′为可调节储能元件的数量；xi（t），νi（t）分别为智能体的位置和速度，分别表示系统第i个功率调节电源在t时刻的功角和转子加速度；ui（t）为交直流混联电力系统暂态过程中可控制出力的可再生能源发电系统出力。

根据所给出的交直流混联电力系统暂态过程动力学模型，考虑系统在暂态过程中交直流系统均存在能量控制过程的不匹配干扰和匹配干扰等多源暂态能量干扰。交直流混联电力系统暂态过程中，常规的火电机组和储能设备作为能量调节主要来源，其智能体动力学模型为

式中：i={1，2，…，n，n+1，…，j}，n为交直流混联电力系统暂态多智能体动力学模型中跟随者的个数，即可再生能源发电系统的个数，其中，j={n+1，n+2，…，n+k}，n，k为常规火电机组和储能的个数；xj（t），νj（t）分别为常规火电机组和储能设备的功角和角速度。

为解决可再生能源发电系统能量控制过程的不匹配干扰，通过设计交直流混联电力系统暂态过程能量控制的非线性干扰观测器，在有限时间内对交直流混联电力系统总的能量平衡状态和能量控制过程的能量干扰大小进行估算。基于对能量干扰的估算，设计出带有前馈补偿项的交直流混联电力系统暂态过程能量控制的复合分布式积分滑模控制算法。

对于包含大量可再生能源等值同步电源节点的交直流混合送出型送端电网，其系统可描述为

根据能量扰动量d的估计值，设计交直流混合送出型送端系统暂态能量控制过程的干扰观测器如下：

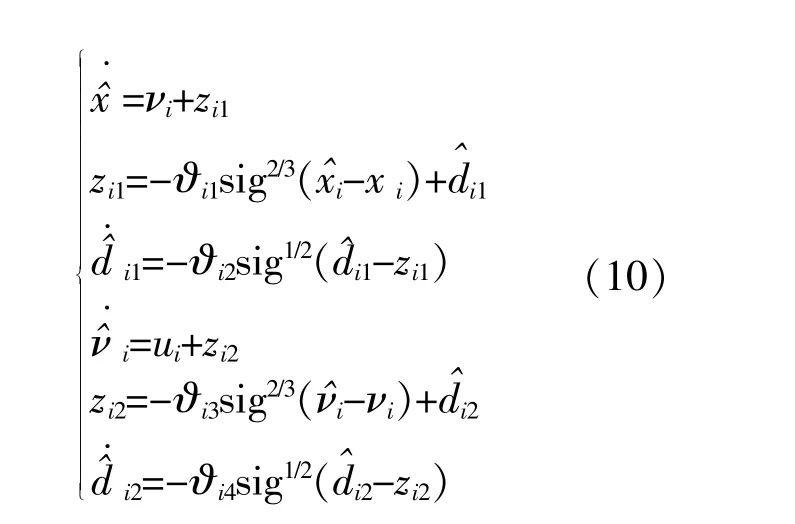
3.2 交直流混联电网暂态能量复合多智能体与分布式控制设计

根据交直流混联电网暂态过程中能量变化过程及风光电源调节的动态特性及其不确定性，建立基于滑模控制的多智能体与分布式控制系统协议，消除交直流混合送出型送端系统暂态过程干扰。设送端系统电源的能量跟踪误差为

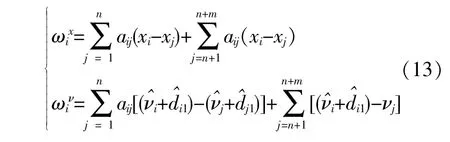
当t=0时，si（0）=0，表示各可控智能体即等值同步电源与分布式的控制状态从初始时刻就位于非线性滑模面上。

当切换增益满足k0＞δ时，基于有限时间干扰观测器和非线性积分滑模面的复合分布式非线性积分滑模控制模型，可使交直流混合送出型送端系统暂态能量实现全局有限时间包容控制。

4 数值仿真

为验证本文所提出的基于考虑可再生能源不确定性的暂态功角有限时间控制模型的有效性，以我国北方某可再生能源送出型电网网架结构数据为基础进行仿真算例分析。

仿真系统拓扑结构如图2所示。

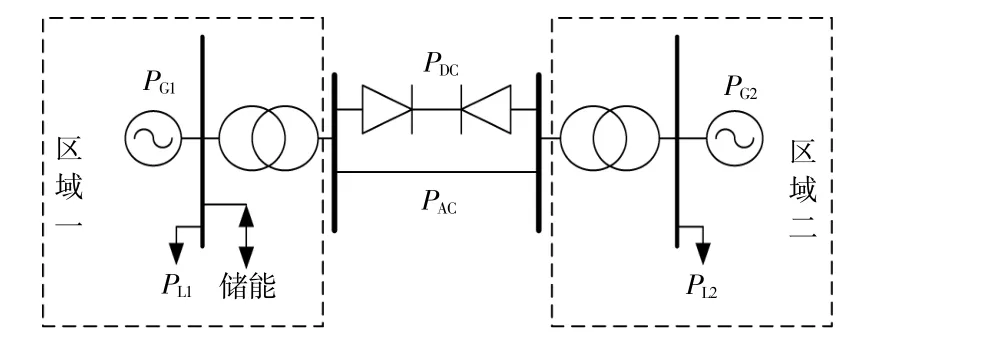
图2 仿真系统示意图Fig.2 Simulation system diagrammatic sketch

区域一和区域二分别为可再生能源交直流送出型电网和受端电网，区域之间通过一条直流输电线路和一条交流输电线路相连。区域一等值同步机容量为1 500 MW，风电等值容量为1 000 MW，风电场输出功率随机扰动取值2%，储能为400 MW，负荷为1 000 MW。区域二等值同步机容量为1 000 MW，风电等值容量为1 000 MW，风电场输出功率随机扰动取值2%，负荷为3 500 MW。

假设送端系统交流线路在1 s时发生单相短路故障，故障持续时间为0.1 s。为验证文章所提方法的有效性，设计系统运行的两种方式：方式一采用传统功角控制模型；方式二采用本文所提出的可再生能源交直流送端电网暂态能量控制模型。对比分析可再生能源交直流混合送出型送端电网采用方式一和方式二运行的状况。

图3为两种运行方式下的发电机功角曲线。采用方式二的可再生能源交直流混合送出型送端电网功角摆动的幅度和速率明显下降，且恢复速度较快；采用方式一的可再生能源交直流混合送出型电网在1 s处暂态功角曲线出现明显的上升并逐步发散。因此，有限时间控制方式有效地抑制了送端电网单相短路故障对功角摆动的影响。

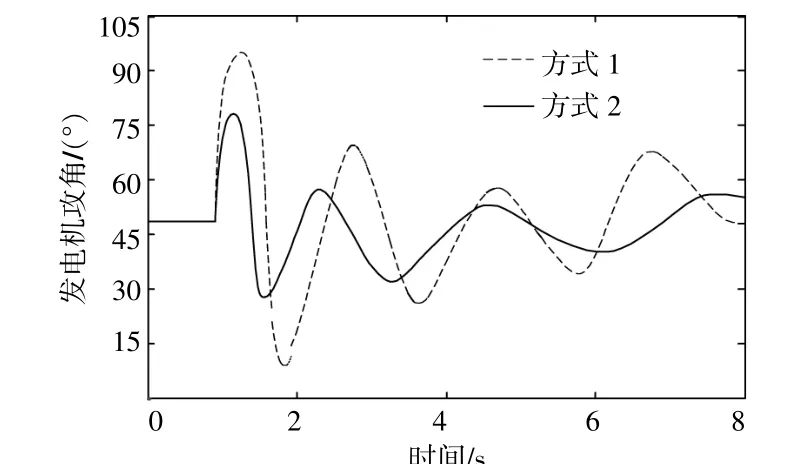
图3 发电机功角曲线Fig.3 Generator power angle curve

图4为直流线路功率曲线。由图4可知，交流线路单相短路后，直流联络线功率出现约为600 MW的波动，6 s后振荡未平息。相较于方式一的传统控制方法，采用方式二的能量控制方法可明显减弱直流联络线功率波动，且在5 s后达到有效抑制。

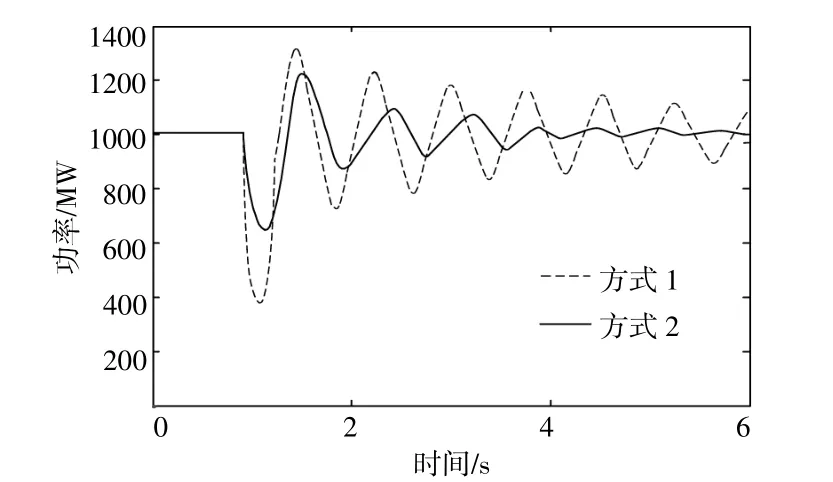
图4 直流功率曲线Fig.4 DC power curve

图5为频率偏移曲线。由图5可知，采用方式一的电网频率偏差曲线在故障发生时出现急剧的上升，并出现明显的尖点；采用方式二的电网频率偏差曲线波动幅度较小，在0.15 s左右未出现明显的尖点，并且恢复速度较快。可见，本文所提的考虑可再生能源交直流送端电网暂态功角有限时间控制有效地抑制了可再生能源交直流混合送出型送端电网的频率波动，同时，将可再生能源送出型交直流电网的频率偏差控制在[-1.2，1.7]，符合[-2.5，2.5]的要求。在故障发生0.5 s后，采用可再生能源交直流送端电网暂态功角有限时间控制的电网频率逐渐接近稳态。

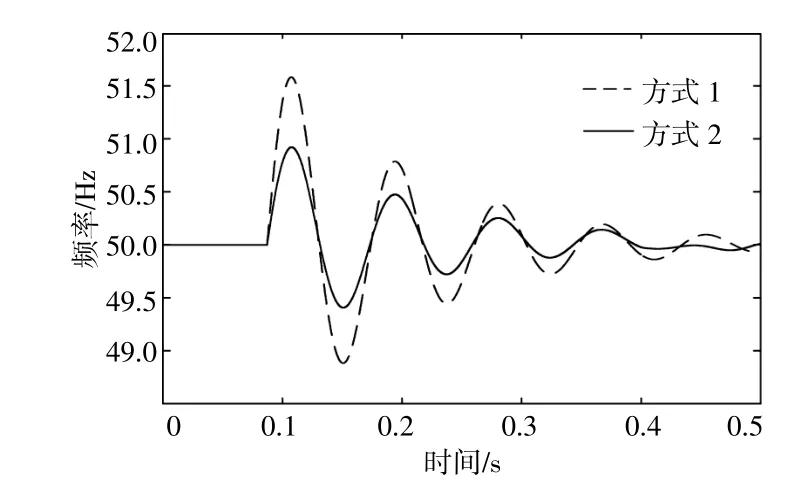
图5 频率偏差曲线Fig.5 Frequency deviation curve

为验证在多场景可再生能源出力不确定条件下，即在风电场输出功率随机扰动参数取值不同时，可再生能源交直流送端电网暂态能量控制模型的有效性，文章设置风电场输出功率随机扰动参数分别为2%，6%和10%，分别采用方式一和方式二的两种送端系统控制策略进行仿真分析。图6为风电场输出功率随机扰动参数分别为2%，6%，10%条件下的送端电网频率偏差标幺值。

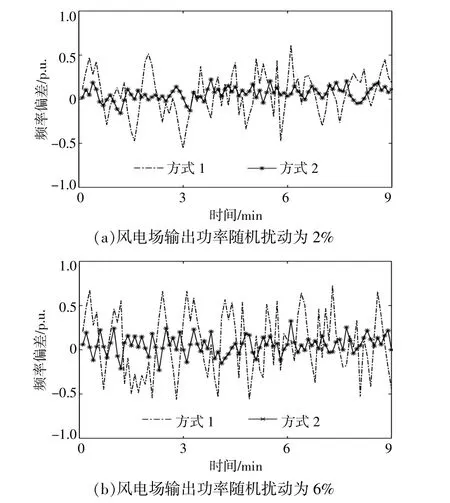
图6 不同风电扰动下的频率偏差Fig.6 Frequency deviation under different wind power disturbances

由图6可知，风电场输出功率的波动将对送端电网频率产生影响。与方式一相比，方式二控制策略对于风电不确定性的抑制效果更佳。通过对比图6（b）和图6（c）可知，在6%和10%的风电场输出功率随机扰动下，本文所提的交直流送端电网暂态能量控制模型对风电波动的抑制均取得较好的效果。方式一的频率偏差随着风电功率扰动的增加而增加，具有线性对应关系，对系统稳定性影响较大。

图7为风电场输出功率随机扰动参数取值分别为2%，6%和10%条件下的送端电网调节成本。由图7可知，与方式一相比，在不同风电扰动下，方式二的送端电网调节成本较低。在10%的风电场输出功率随机扰动下，由于方式二中的可再生能源可作为调节资源，系统的调节成本整体并没有类似于方式一那样呈线性增加。由此证明，本文所提出的方法能够有效协调可再生能源送出型交直流电网中各种可调节的资源，对大扰动下的暂态过程以及可再生能源不确定性，具有较好的暂态能量控制能力。

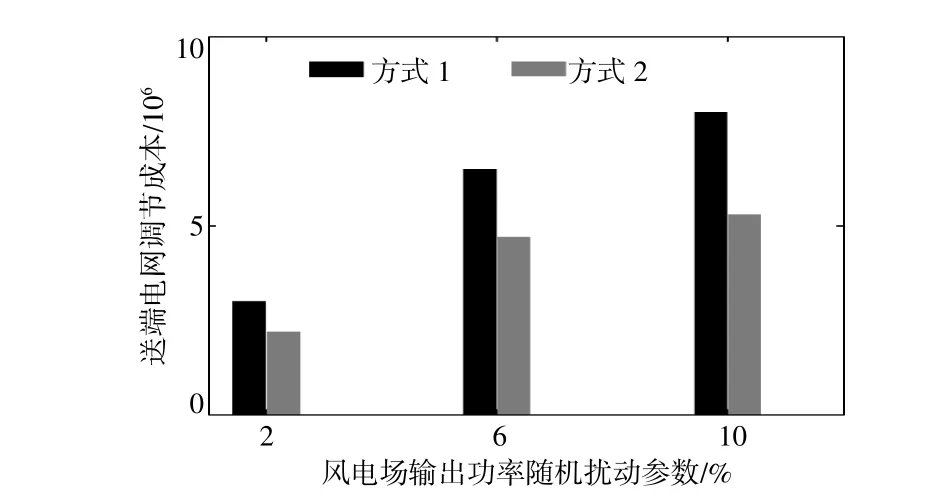
图7 不同风电扰动下的送端电网调节成本Fig.7 Transmission-end grid regulation costs under different wind power disturbances

图8显示了二阶多智能体系统的两个领导者和3个跟随者的运动轨迹。可以看出，在t=8 s时，3个跟随者的位置收敛到两个领导者的平面范围中，二阶多智能体系统实现了包容控制。

图8 多智能体运动轨迹Fig.8 Multi-agent motion trajectory

5 结束语

本文提出一种考虑可再生能源送出型交直流电网暂态能量有限时间控制方法。为了观测交直流混联电网暂态能量状态，设计了交直流混联电网暂态能量复合分布式控制，以观测系统动态特性及其不确定性。本文以图论的方法研究了二阶多智能体系统的有限时间包容控制问题。仿真结果验证了考虑可再生能源不确定性的暂态功角有限时间控制模型，具有较好的功角稳定以及频率偏移的控制效果。