一种用于光伏系统的具有自均压能力的多电平升压型逆变器

李飞高，孟艳花

（1.河南职业技术学院，河南 郑州 450046；2.河南工业大学，河南 郑州 450001）

0 引言

目前，多电平逆变器在可再生能源系统、电动汽车和电机驱动应用等领域发挥着关键作用[1]。与两电平逆变器相比，多电平逆变器在谐波失真、电磁干扰、电压应力等方面具有明显优势，且其输出质量好、效率高。又因其具有易于模块化制造、容错能力强、可靠性好、功耗低等特性，已得到广泛应用[2]。

针对多电平逆变器体积较大的问题，近年来一些学者提出了多种优化方案，例如采用减少直流电源和功率半导体器件数量的方式降低整体成本和复杂性[3]。由此引入了基于开关二极管[4]和开关电容[5]，[6]的拓扑结构。此外，基于电容的逆变器拓扑需要外部电压平衡电路以维持电容两端所需的电压水平。在提高电平的前提下，为减少器件的使用，文献[7]，[8]提出具有两倍升压能力的拓扑。文献[9]～[11]提出了使用相对较多开关器件从而具有四倍升压能力的拓扑。文献[12]减少了开关数量，但使用了更多的电容器和二极管，导致器件冗余度较高，控制复杂。

本文提出了一种适用于光伏系统的新型九电平SC-MLI（N2MLI）。该电路拓扑结构简单易行，具有较少的器件数量和较低的器件电压应力，具备电容电压自动平衡功能，拥有一定的优越性和应用价值。

1 所提逆变器拓扑结构

图1（a）为本文所提升压型九电平逆变器拓扑。该逆变器由9个开关管、一个二极管和两个电容器（C1，C2）构成。此外，仅使用PV作为输入源以合成九电平输出并为电容器充电。所提逆变器在离网或并网应用中，与单个模块控制的多直流多电平逆变器[13]相较而言，由于器件的减少，最大功率跟踪、直流母线平衡和控制策略均得到简化。其中，输入端仅使用一个可变直流电源，无需外部平衡电路即可将开关电容充电至所需电平。开关电容C1和C2采用串、并联充电和放电技术，分别在电平为Vdc和2Vdc时实现自平衡。C1在输出电压为0，±1Vdc，±3Vdc的阶跃期间充电，而C2在±2Vdc时充电。值得注意的是，总充放电周期的持续时间小于输出半周期的持续时间，因此可确保电容电压快速恢复。另外，电容在正、负半周期内对称放电，如图1（b）所示。

图1 所提逆变器结构Fig.1 Proposed inverter structure

图1（c）示出了所提逆变器的详细工作原理。输入直流电源产生初始电平Vdc，同时通过开关管S2将C1充电至Vdc。此时，C2保持理想状态，通过开关管S5充电至2Vdc，然后传递至输出端。在所有奇数与偶数电压阶跃期间，C1分别通过开关管S2和S1连续充电和放电。在生成电压3Vdc阶跃期间，C2放电之后所有电容电压值与输入源相加，在输出端为4Vdc。通过关闭开关管S6和S7，负电压阶跃产生与正电压阶跃类似。此外，所提逆变器可适用于任何低或高功率因数负载。图1（d）示出了在阻感负载期间电流的续流回路。

2 比较分析

本文所提九电平逆变器与CHB，NPC，FC逆变器就所需器件数量进行了比较，详见表1。对所提逆变器与其他类似拓扑在开关管、二极管、电容、TSVS和电压增益等方面做出了进一步的比较，结果如表2所示。与文献[2]，[6]，[7]，[12]中的拓扑相比，所提逆变器仅需较少开关管和二极管即可实现九电平输出。文献[9]～[11]中的拓扑虽无需二极管，但开关器件相对较多，控制策略较为复杂。在含开关电容的多电平逆变器中，电容器的数量通常决定输出电压电平的数量。从表中可以看出：文献[2]，[7]，[9]中的拓扑与所提逆变器只需使用较少电容器即可实现九电平输出；文献[2]的拓扑在TSVS方面具有较大优势；但文献[2]，[7]中的拓扑升压能力较弱，应用场景受限。

表1 常规多电平逆变器的比较Table 1 Comparison of the conventional multilevel inverters

表2 单相直流九电平逆变器的比较Table 2 Comparison of single-phase single DC nine-level inverters

续表2

3 控制策略

现有多电平逆变器一般采用两种控制策略，即高开关频率脉宽调制控制和选择性谐波消除（Selective Harmonic Elimination，SHE）控制。前者基于载波信号与参考信号比较[1]，后者广泛用于低电压水平场合[4]，开关损耗较小。鉴于此，本文采用SHE控制策略验证所提逆变器的可行性，其中详细的PI参数设计过程和建模分析见文献[4]。SHE控制策略通过消除低次谐波从而有效降低总谐波失真，但若应用于数量较多的电压电平，需通过实施优化算法求解非线性超越方程，从而增加了系统复杂性并影响了瞬时动态响应。考虑到逆变器的输出具有对称性，其阶跃输出电压波形可用傅里叶级数方程表示为

因此，考虑在文献[4]中给出的代价函数，并满足式（4）给出的边界条件，可求得本文非线性方程。

4 仿真结果分析

为分析动态条件下所提逆变器的性能，在MATLAB/Simulink平台上搭建了仿真模型。图2示出了MI值分别为0.25与0.9时输出电压Vo以及电容电压VC1和VC2的波形。相应的谐波分布如图2（c）所示。尽管THD值在MI=0.9时相对较高，但无论MI值如何变化，Vo几乎保持不变。因此，电容电压可保持在所需值而无需任何外部平衡电路。图2（d）示出了不同开关管的PWM脉冲。值得注意的是，每个模态只有少量开关处于导通状态。图2（e）示出了所有开关上的电压应力，验证了TSVS的合理性与开关管的单向特性。

图2 N2M LI仿真结果Fig.2 Simulation results of the N2MLI

从图2（b）九电平输出阶梯波形中可以看出，C1的最高放电周期为（θ4～π-θ4）/ω，C2的最高放电周期为（θ3～π-θ3）/ω。因此，C1和C2分别选取2 200μF和3 300μF的电容。输入直流电压设置为25 V，则C1和C2分别在25 V和50 V处自平衡，且在输出端产生峰值电压为100 V。为求得合适的目标函数，通过计算机编程求解与SHE控制相关的非线性傅立叶级数方程，不同MI值的开关角度结果存储在查找表中，从而得到目标函数的最优值为0.9，此时THD最小。

为验证所提逆变器的可行性，本文采用了不同的负载组合，如阻性负载（R）与串联阻感性负载（RL），频率设为50 Hz。仿真结果如图3所示。

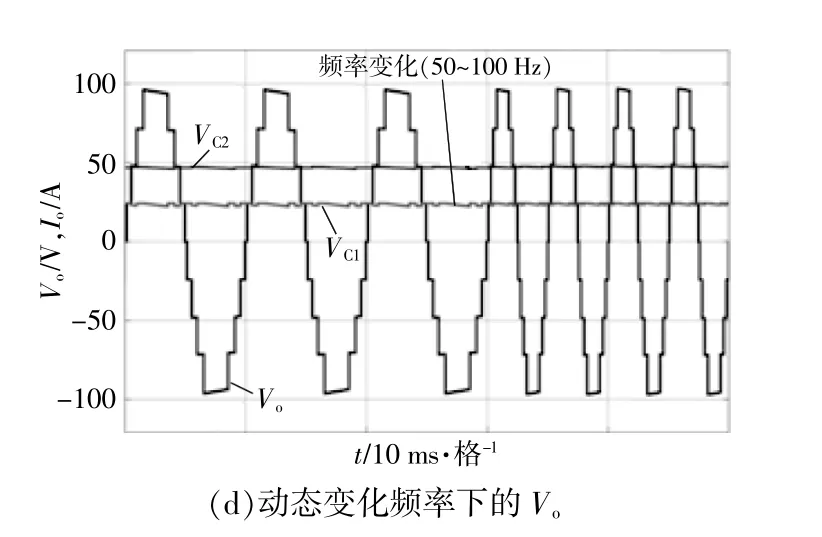
图3 仿真结果Fig.3 Simulation results

5 性能验证

为进一步验证理论分析的正确性及所提逆变器的可行性，本文搭建了一台实验样机，如图4所示。

图4 M LI拓扑的测试安装Fig.4 Test installation of MLI topology

其中：采用9个12N60A4D绝缘栅双极晶体管开关管和一个RGP30D功率二极管；所用电容器定值与模拟电容器相同，通过25 V的单输入直流电源充电。该实例在DSP控制器中编程，产生PWM脉冲用于所提逆变器。TLP250栅极驱动电路用于放大由DSP控制器产生的脉冲。实验结果如图5所示，其中图5（a）和（b）所示与图2（a）和（b）相同。电容电压VC1和VC2分别在所需值为25 V与50 V时自均衡，不同MI值时Vo的基波值均保持不变。图5（c）示出的THD曲线表明，由3次、5次、7次构成的所有目标低阶谐波均可在较高MI的输出电压波形中滤除。

图5 不同M I下N2M LI的实验结果Fig.5 Experimental results of N2MLI under different MI

保持MI值为0.9，纯电阻负载与动态负载的实验结果如图6所示。由图可知，输出电流Io幅度随着负载的增加而减小，但在此测试条件下电压波形不受影响。同时，由于存在电流续流回路，因而所提逆变器也可在高电感负载下正常工作。因此，所提逆变器可实现在高、低频负载下运行。

图6 实验结果Fig.6 Experimental results

6 结论

本文提出了一种由9个开关管、1个二极管和2个电容组成的新型单直流九电平逆变器。通过巧妙的电容位置设计，消除了外部平衡电路并提高了升压能力。与其他相似拓扑的对比分析可知，所提逆变器更具优势。值得注意的是，随着工作频率的增加，自平衡电容两端的电压纹波可进一步减小。同时，大多数开关管工作在工频状态，则所提逆变器开关损耗较小。此外，不同动态测试条件下的平稳运行验证了非理想环境下的有效性。