Menger PN空间中非线性算子方程一般解的存在性研究

陈方杰

(桐城师范高等专科学校 商贸与电子信息系，安徽 桐城 231400)

1 相关概念

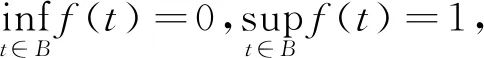
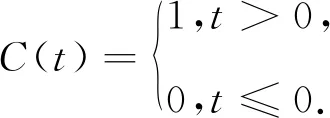
(1)

定义t-范数Δ为不间断[2].

Menger PN空间是Menger概率线性赋范空间[3-4],即有序三元组(E,F,Δ),E表示实线性空间,F为E到M的映射,定义fx符合以下要求(研究中fx即为F(x),fx(t)是分布函数fx在t∈B处的值).

fx(0)=0,∀x∈E,fx(t)=H(t),∀t∈B,只有x=ε时成立,φ≠0的随机实数,存在fφx(t)=fx(t/|φ|),随机的x,y∈E，t1,t2∈B+,存在fx+y(t1+t2)≥Δ(fx(t1),fy(t2)).

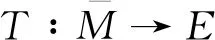
(i)Deg(N,M,u)=1,∀u∈M；

(ii)Deg(W,M,u)≠0,此时W(x)=u在M中存在解；

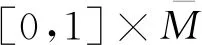
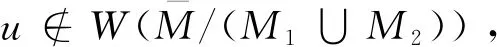
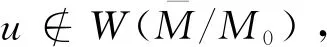
(vi)定义u∉W(γM),那么Deg(W,M,u)=Deg(W-u,M,ε).

引理1定义(E,F,Δ)表示Menger PN空间,Δ为连续,那么概率分布函数f为下半连续,即随机t∈B,若当n→∞时，qn→q和pn→p,那么,

(2)

引理2定义无限维Menger PN空间(E,F,Δ)中存在开子集M,随机t∈[0,1],t-范数Δ满足Δ(t,t)≥t.T∶M→E为连续紧算子，满足

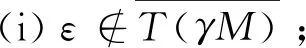
(ii)随机η∈[0,1]，x∈γM,存在Tx≠ηx.

因此Deg(N-T,M,ε)=0.

2 主要结论

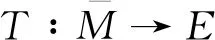
fTx(w)>fφx(w),∀s>0,∀x∈γM,

(3)

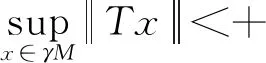
定义ct(x)=x-Ct(x),验证：随机t∈[0,1]存在ε∉ct(γM),反之,定义有t0∈[0,1],x0∈γM,则ε=ct0(x0),因此得到

φx0=t0T(x0).

(4)

(5)

上述结果显示公式(5)与公式(iii)相斥,所以,随机t∈[0,1]存在ε∉ct(γM)情况成立.由Leray-Schauder度性质(iii)可知Deg(N-T/φ,M,ε)=Deg(N,M,ε).同时ε∈M,考虑Leray-Schauder度性质(i)得到以下形式

Deg(N,M,ε)=1.

(6)

根据Leray-Schauder度性质(ii)得到以下结论[5]有x1∈M,令Tx1=φx1.

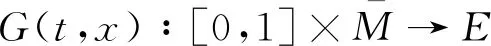
接下来验证：随机x∈γM,t∈[0,1]存在x≠G(t,x),否则,定义有t1∈[0,1],x2∈γM,可令x2∈G(t1,x2),即可表示成x2=t1T(x2)+φy0,因此得

(7)

(8)

所以,φy0∉M,那么Deg(N,M,φy0)=0,则

Deg(N-T-φy0,N,ε)=0.

(9)

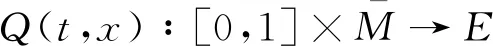
(10)

引理3若y>1,φ>1,0<ρ<1,则下式成立.

ρ+(1-ρ)yφ>[ρ+(1-ρ)y]φ.

(11)

证明设f(y)=ρ+(1-ρ)yφ-[ρ+(1-ρ)y]φ,那么f(y)为可导函数,存在

f′(y)=φ(1-ρ)yφ-1-φ(1-ρ)[ρ+(1-ρ)y]φ-1

=φ(1-ρ)[yφ-1-(ρ+(1-ρ)y)φ-1]>0.

(12)

由于存在以下形式y-1,1-y<0,ρ(1-y)<0,且0<ρ<1,所以0<ρ+(1-ρ)y=ρ(1-y)+y1.

所以函数f(y)在[1,+∞]中严格单调增[6],在此情况下,若y>1,f(y)>f(1),f(1)=0,则f(y)>0,也可用如下形式表示

ρ+(1-ρ)yφ>[ρ+(1-ρ)y]φ.

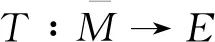
(13)

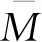
证明定义Tx≠ηx,∀x∈γM,η≥1.

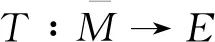
同样为紧性连续算子.

要求

接下来验证εcw(γM),W∈[0,1],定义ε∈cw(γM),则可知W0∈[0,1],x0∈γM,致使

即：ηx0-W0Tx0=ε,那么W0≠0,反之,ηx0=ε,⟹x0=ε∈γM与ε∈M相斥.

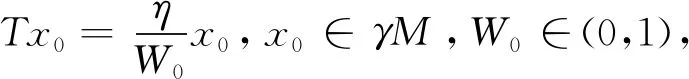
0<ρ<1,φ>1,00.

即

即

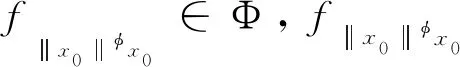
(14)

则存在

(15)

ρ+(1-ρ)yφ<[ρ+(1-ρ)y]φ.

(16)

由于W0∈(0,1),η≥1,所以y>1,同时φ>1,0<ρ<1,因此公式(16)和引理3相斥.

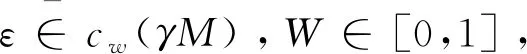
(17)

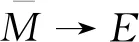
因此,u≠(N-T)(γM),同时Deg(N-T,M,u)=Deg(N-T1,N,u).

证明根据条件(Z2)可知∀t>0,x∈γM时

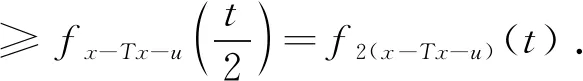
(18)

即

fx-Tx-u(t)≥f2(x-Tx-u)(t).

(19)

若u∈(N-T)(γM),必定存在x0∈γM,令u=(N-T)x0,即

Tx0=x0-u.

(20)

根据公式(18)获取以下形式

fx0-T1x0-u(t)≥f2(x0-Tx0-u)(t).

(21)

结合公式(20)和(21)得fx0-T1x0-u(t)≥C(t),t>0,因此x0-T1x0=u.由于x0∈γM,则x0-T1x0=u同u∉(N-T1)(γM)相斥,那么u∉(N-T1)(γM).

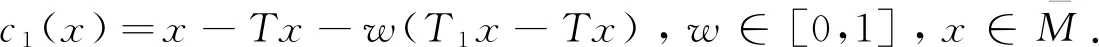
假设u∈(N-T1)(γM),则∃w0[0,1],x1∈γM,所以得到

u=x1-Tx1-w0(T1x1-Tx1),

(22)

同时令w0≠0,w0≠1,根据公式(22)得

x1-Tx1-u=w0(T1x1-Tx1).

(23)

结合(Z2)与公式(23)得

(24)

设置n→∞,则fx1-Tx1-u(t)=C(t),t>0.所以u=x1-Tx1,同时x1∈γM和u∉(N-T)(γM)相斥,因此,u∉c1(γM),w∈[0,1].基于同伦不变性原理可知Deg(N-T,M,u)=Deg(N-T1,N,u).

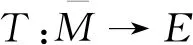
(Z3)fTx(t)≥fJx+u(t)，

(25)

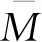
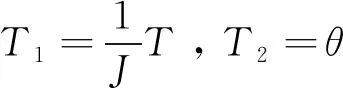
(26)

(27)

根据(Z3)得到

fTx(|J|t)≥fJx+u(|J|t).

(28)

结合公式(26)、(27)和(28)得到

(29)

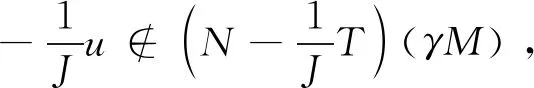
(30)

本文提出的三种不同的非线性算子方程各自存在特定特征.定理 1提出的非线性算子方程为左连续函数,定理 2提出的非线性算子方程为右连续函数,定理 3提出的非线性算子方程为非减非连续函数.这三类非线性算子方程为Menger PN空间中典型方程,求取其解的存在性具有代表性.