基于改进粒子群算法的蛋白质结构预测

李明珠

（黑龙江中医药大学基础医学院，黑龙江 哈尔滨 150040）

0 引言

生物信息学运用计算机软、硬件技术对生物学数据进行计算、分析和数据挖掘，极大地提升了生物数据信息解算的效率，对更准确地掌握生物体结构运行规律具有十分重要的意义[1]。蛋白质分子构成了人体的组织和器官，蛋白质的空间结构决定了蛋白质的生命功能，进而也影响甚至决定着人体的生命活动。许多疾病的出现就是因为蛋白质分子的结构遭到破坏或者发生变异，使蛋白质失去了稳定状态[2]。蛋白质结构预测的分析方法可以分为3类：比较建模法、反向折叠法和从头预测法。比较建模法和反向折叠法需要已知的蛋白质结构作为模板，而从头预测法不需要。因此，从头预测法可以对未知信息的蛋白质结构进行预测，前提是构建出一个具有针对性的能量函数模型[3]。蛋白质结构预测领域已经出现了很多方法，但蛋白质稳定结构对应的最低势能值点的准确预测依然是一个难点。加之蛋白质对应的数据量庞大，对算法的收敛速度和精度都有较高的要求。为此，该文在粒子群算法的基础上进行改进，融入禁忌搜索策略，以提升其在蛋白质结构预测时的性能。

1 蛋白质结构模型

蛋白质结构预测问题其实是一个复杂多项式的非确定性问题，即NP完全问题。该文选择从头预测法作为解决蛋白质结构预测问题的方法。因此，首先需要确定蛋白质结构的简化模型。通过构建简化模型，将蛋白质结构和能量的关系模拟为一个势能函数。然后利用热力学假说，蛋白质势能函数值最低时即为蛋白质最稳定的结构。

目前，主要有2种较为常用的简化的蛋白质结构模型，一种是HP格点模型，另一种是AB非格点模型。

在二维平面上，模拟蛋白质折叠结构的二维HP格点模型和二维AB非格点模型的结构如图1所示。

图1（a）表示二维HP格点模型。在HP模型中，将氨基酸分成疏水性氨基酸和亲水性氨基酸，分别用英文字母H和P表示。黑色方块为疏水性氨基酸H，白色方块为亲水性氨基酸P，每个互相连接的氨基酸之间的距离都为1。而且每个格点都必须放在二维平面的整数点上，即互相连接的氨基酸残基之间的角度不能改变。黑色方块聚集在一起，即疏水性氨基酸集中在亲水性氨基酸的内部，形成一个疏水核心，疏水键用来维持蛋白质结构的稳定。

图1（b）表示二维AB非格点模型。与HP格点模型一样，AB非格点模型也将常见的20种氨基酸分成2类，一类为疏水性氨基酸，用英文字母A表示；另一类为亲水性氨基酸，用英文字母B表示。不过，和二维HP格点模型相比，AB非格点模型中相邻氨基酸之间的角度是可变的，而不是固定在二维平面的整数点上。这种结构跟真实的蛋白质空间结构更相似，用来作为蛋白质的模拟结构更合适。图1（b）中带有数字的白色方块代表氨基酸，相邻2个氨基酸的残基之间会形成夹角，用α1、α2、α3……表示。

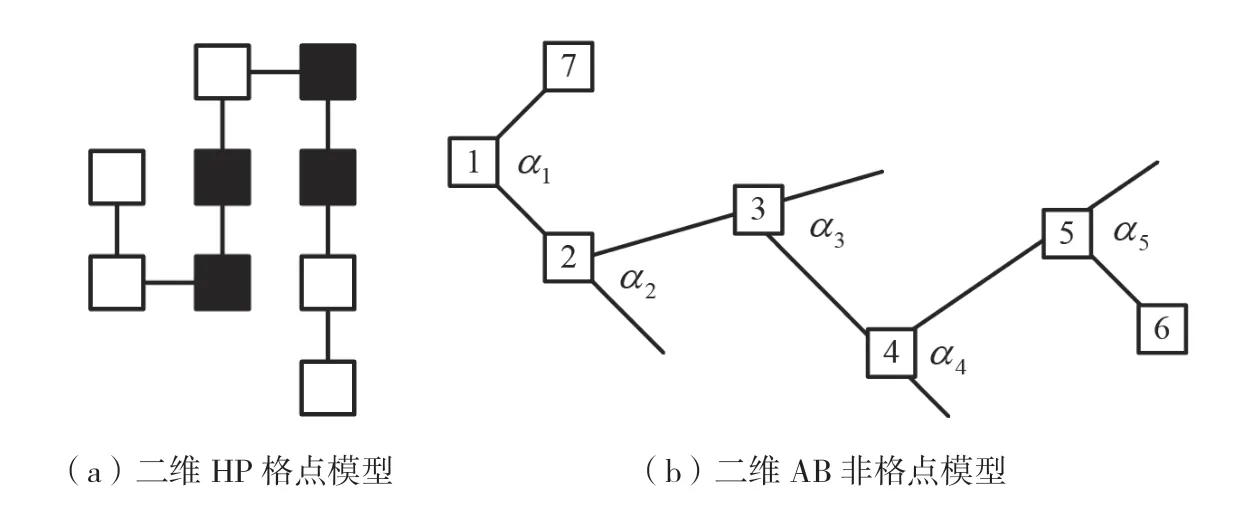
图1 二维HP模型和AB模型

二维AB非格点模型的能量函数的表达如公式（1）所示。

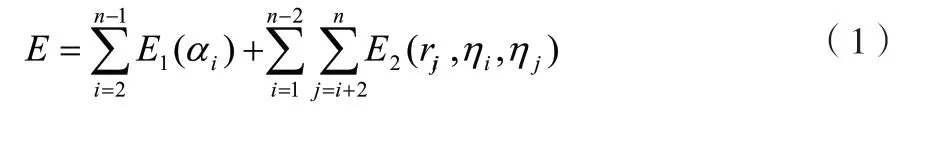
式中：E为能量函数；n为氨基酸数目；E1为第一部分势能函数，表达的是氨基酸骨架折叠所蕴藏的能量，与各个折叠角度有关；E2为第二部分势能函数，表达的是不相邻氨基酸残基之间的能量，与残基之间的距离和极性有关。

综合对比HP格点模型和AB非格点模型的优缺点，该文的算法中均采用AB非格点模型对蛋白质结构进行表达。

2 蛋白质结构预测算法设计

2.1 蛋白质结构预测算法的总体构思

蛋白质的稳定结构对应于蛋白质势能函数的最低能量值，这就使蛋白质稳定结构的预测转变为能量函数的寻优问题。在这一领域，禁忌搜索法和粒子群算法都是比较常见的方法。

因其具有的良好的记忆功能，禁忌搜索算法对局部搜索的能力很强。通过使用禁忌表记录已经搜索过的局部最优解，禁忌搜索算法可以避免迂回搜索、跳出局部最优。同时，通过藐视准则激励某些较好的解，禁忌搜索算法也可避免错失优良个体。

但是禁忌搜索算法对初始解有一定的依赖性。较好的初始解能够让禁忌搜索算法搜索到较优的值，较差的初始解将导致禁忌搜索算法的收敛速度降低。

粒子群算法能够得到较好的解。因此，该文将粒子群算法得到的较好解作为禁忌捜索算法的初始解，然后利用禁忌搜索算法的禁忌策略和藐视准则形成一个既有全局捜索能力又有局部搜索能力的优化算法。

2.2 蛋白质结构预测算法的详细设计

2.2.1 初始值的生成

运行粒子群算法进行全局搜索。待收敛到一定程度后，将得到的较好的解作为禁忌搜索算法的初始值，进而提高算法的搜索精度和效率。

每个粒子的速度和位置更新方式如公式（2）和公式（3）所示。

式中：ϑ为惯性权重；λ1和λ2分别为2个学习因子；rand（）为随机函数；pid为第i个粒子的历史最优位置；pgd为整个粒子群的历史最优位置。

2.2.2 邻域函数

禁忌搜索算法的邻域解通过单点变异实现。该文采用扰动变异的丝线来产生邻域解，以便保证邻域解的多样性。此处设计的邻域函数如公式（4）、公式（5）所示。

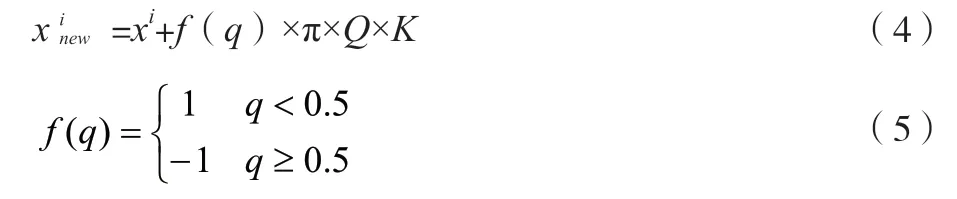
式中：q和Q分别为随机数；K为比例因子；i为邻域解的生成次数。如果邻域解的个数为L，那么i在[0，L-1]取值。此处设定K=0.93，L=40。

2.2.3 候选解集

候选解集是邻域解的一个子集。在算法中，通过计算L个邻域解中每个解的适应值，选择适应值最低的前LC个邻域解作为候选解集。此处设定LC=6。

2.2.4 禁忌表

禁忌表用来存储近期搜索过的解，其长度为LT。每次算法经过迭代后，新的禁忌对象会进入禁忌表。与此同时，每个禁忌对象的任期应该减1。只有当禁忌对象的任期为0时才能够被解禁，先进入禁忌表的对象可以先被禁忌出去。禁忌表的长度对算法的搜索精度也有一定影响。如果禁忌表的长度较大，则算法的搜索范围相对较广，能够搜索到较好的解。但是这也会使算法的搜索时间变长，收敛速度变慢。如果禁忌表长度过小，就不能发挥禁忌表的作用，容易使算法陷入迂回搜索。所以，禁忌表长度的设置是否合理将对算法的结果有很大影响。此处设定LT=8。

2.2.5 禁忌准则

设候选解z（α1，α2，…，αn-2）的适应值为E（z），禁忌表中存在一个解向量y（α′1，α′2，…，），其适应值为E（y），如果满足公式（6）和公式（7），那么候选解z满足禁忌准则，候选解被禁忌。

此处，根据多次试验的结果，设E0=0.10，r0=0.005。

3 试验结果与分析

3.1 试验配置

为了验证该文提出的蛋白质结构预测方法的有效性，接下来进行试验研究。试验中所用的计算机CPU为Intel双核，单核主频3.60 GHz，内存大小为16 GB。计算机的操作系统为windows 10。

试验中，该文算法参数的配置如下：粒子群算法的粒子总数为260个，迭代次数上限为800，2个学习因子λ1=λ2=2.0，比例因子K=0.93，邻域解个数L=40，候选解个数LC=6。

试验中，为了和该文算法形成对比，还选择了粒子群算法和禁忌搜索法作为试验中的对照方法。

试验中，试验对象选择了试验标准常用的人工蛋白质序列，共分为4组。4组人工蛋白质序列都采用AB非格点模型表示，第一组人工蛋白质序列的长度为13，包括5个亲水性氨基酸（A），8个疏水性氨基酸（B）；第二组人工蛋白质序列的长度为21，包括8个亲水性氨基酸（A），13个疏水性氨基酸（B）；第三组人工蛋白质序列的长度为34，包括13个亲水性氨基酸（A），21个疏水性氨基酸（B）；第四组人工蛋白质序列的长度为55，包括21个亲水性氨基酸（A），34个疏水性氨基酸（B）。4组人工蛋白质序列的氨基酸配置如图2所示。

3.2 蛋白质结构预测结果

根据上述4组人工蛋白质序列，分别按照禁忌搜索法、粒子群算法和该文算法构建数学模型，并执行最低势能值预测，结果见表1。

从表1中的试验结果可以看出，该文算法得到的4组人工蛋白质序列的最低势能值，都要明显低于禁忌搜索法和粒子群算法得到的最低势能值。这也表明，利用该文算法可以得到更稳定的蛋白质结构。

表1 3种方法得出的最低势能值

进一步，对上述4组人工蛋白质序列的稳定结构进行预测，第二组和第三组蛋白质结构的预测结果如图3和图4所示。

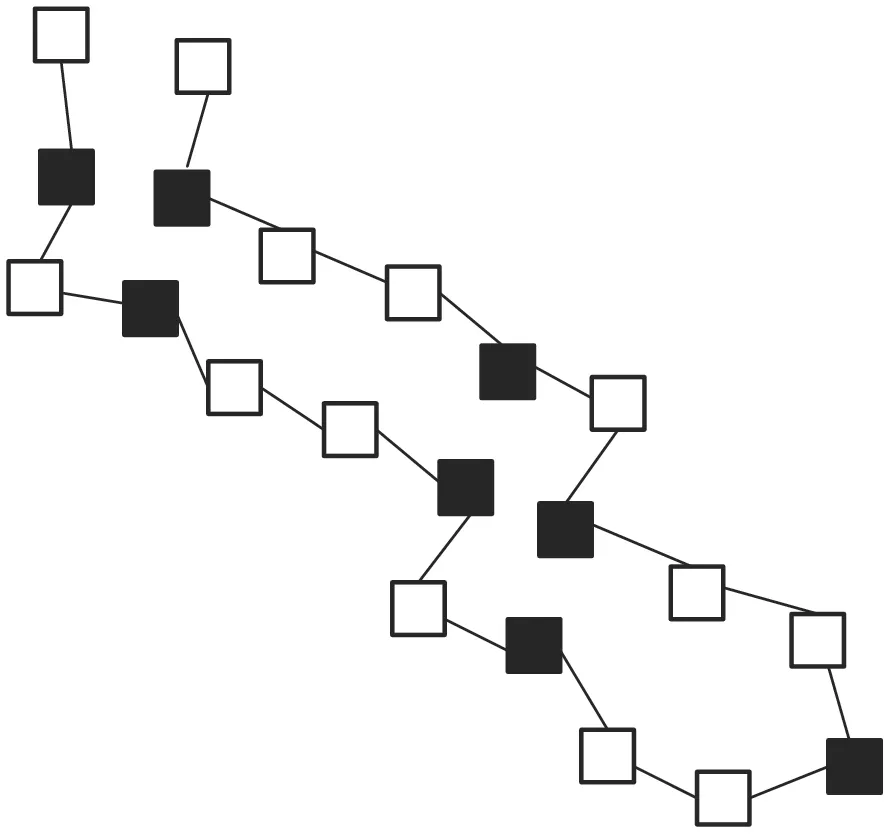
图3 第二组人工蛋白质序列稳定结构的预测结果

图4 第三组人工蛋白质序列稳定结构的预测结果

4 结论

蛋白质序列结构稳定性的研究是生物信息学领域的重要研究内容。该文针对这一问题，将禁忌搜索法和粒子群算法结合起来，提出了一种新的蛋白质结构的预测方法。该方法充分考虑了禁忌搜索法对初始解具有依赖性的问题，先运用粒子群算法求取初始解，然后再运用禁忌搜索法构建邻域函数、候选解集、禁忌表和禁忌准则，通过2种算法的融合完成蛋白质结构的预测。试验中，选取了4组人工蛋白质序列，先按照AB非格点模型建模，进而分别采用3种方法求取最低势能值。试验结果表明，和禁忌搜索法、粒子群算法相比，该文算法得到的蛋白质序列的势能值更低，预测出的蛋白质稳定结构更合理。