模型试验及数值模拟下尾矿库溃坝尾砂流演变预测

罗昌泰， 李栋伟， 余国平， 张潮潮， 徐 斌

(1.东华理工大学 土木与建筑工程学院，南昌 330013； 2.南昌工程学院 土木与建筑工程学院，南昌 330099；3.中国瑞林工程技术股份有限公司，南昌 330038)

尾矿库是用以堆存矿山进行矿石选别后排出的尾矿或其他工业废渣的场所，是一个具有高势能的人造泥石流危险源[1]。Lemphers[2]对世界范围内3 500座尾矿坝进行了统计分析，发现其溃坝失事概率是水库大坝的10倍以上。基于历史事件，Davies等[3]发现尾矿库的溃坝概率在1∶700～1∶10 000。尾矿库溃决所形成的尾砂流将造成下游居民的伤亡和设施的破坏，并造成环境灾害。例如，2008年9月8日山西省襄汾县新塔矿业发生的特大尾矿库溃坝事故，造成281人死亡，34人受伤，并造成环境灾难[4]；2010年9月21日，紫金矿业尾矿库溃坝事件，造成22人死亡，房屋倒塌523户783幢，损坏房屋6 370间[5]。数十年来，这种事故时有发生。随着尾矿坝事故的频发，引起了国内外的高度关注。经统计，地震液化、洪水漫顶和渗流是导致尾矿库溃坝的主要原因，其直接影响是尾矿坝失稳。Rico等[6]分析了全世界147个尾矿库事故，并提出了尾矿坝失稳的主要原因包括高陡坝(10～45 m)、异常降雨和地震液化，记录了218次尾矿库事故，其中极端降雨是主要原因。Yin等[7]通过对玉溪铜矿尾矿库坝体结构的改变(包括降低坝体高度和增加坝体排水管等工艺)进行物理模型试验，验证之后并将该技术工艺应用于实际工程中以加固坝体。

为了预防和减少尾矿库溃坝的事故，许多国家通过立法来规范尾矿库的建造和管理，规定在尾矿库的设计、建设、运行和监测过程中，必须进行严格的评价，防止造成尾矿库的溃坝事故[8]。自20世纪60年代以来，国内外对尾矿库溃坝的形成机理进行了深入、系统的研究[9]。目前对溃坝问题的研究主要有3种方法：理论分析、数值模拟和物理模型试验[10]。早期的研究主要以理论分析为主，但理论研究通常局限于比较简单的情形[11]。随着科学技术的发展和计算手段的进步，数值模拟是当今主流的研究手段，诸多学者通过对尾矿坝的安全性和环境演变进行数值模拟，表明在尾矿库溃坝预测中，冲沙距离、泥沙深度和冲击压力是关键因素[12-13]。物理模型试验在尾矿库溃坝研究中常作为预测这3个关键因素的经验方法，与数值模拟方法进行相互的验证及补充。然而，不同的数值模拟方法采用不同的数学模型，其基本理论、计算公式和方程也不同，比如利用不同的数值计算方法或方案(如：有限元法、有限体积法、概念有限差分方法、离数字高程模型(digital elevation model，DEM)法、光滑粒子流体动力学(smoothed particle hydrodynamics，SPH )方法、浅水波方程法)以及不同的本构模型(如：Bingham，HBP，Voellmy，Cross，and Viscous)来分析尾矿库复杂的溃决特性，这也导致了溃坝结论存在较大的差异。

溃坝形成尾砂流的过程中流体的黏度是增大的，随着浆体黏度的增大，它的冲击力与冲击力标准差呈非线性增大的[14]，在尾矿库溃坝研究中，掌握其溃决后尾砂流的流速、沉积深度和移动距离往往是研究的关键，这对溃决尾砂流的监测、预警和预防是至关重要的。对诸多尾矿库溃坝事件的统计分析发现在坡度相对平缓(300‰以上)的冲沟中，即使在暴雨条件下，冲沟也会保持稳定[15]。局部强降雨引起的尾矿库溃坝是由于暴雨过程中地下水位突然升高，孔隙水压力过大而引起的，导致沟道内岩土体失稳加剧，滑脱加速。但部分尾矿在暴雨过程中，地表附近并没有从排水孔中渗出地下水，监测结果也表明地表附近的地下水位不受暴雨影响[16-17]。

为了阐明尾矿库溃坝尾砂流的运动规律，预测尾砂流的运动距离和作用范围，众多学者采用了Ramms、CFD、DAN3D、SPH、Mass-flow等数值模型来计算其运动规律。其中RAMMS软件使用了双参数Voellmy摩擦模型来表达流动碎片之间的摩擦运动，研究表明，Voellmy摩擦模型能够较准确地模拟尾砂流的运动轨迹[18]。RAMMS软件在标定Voellmy模型过程中通常需要参考记录良好的历史事件，并确定可以在后续分析中使用最佳的拟合参数集。此外，RAMMS软件还可以对DEM或DSM(digital surface model)的结果进行融合，可修改地形数据和增加附加参数的数量，这方便对尾砂流的预测[19]。然而，这些研究尚未得到实际尾矿库溃坝的验证，尾矿库溃坝不同于边坡泥石流，其流道较长、体积较大、流动深度较大，而且可能携带有害物质。因此，有必要开展RAMMS软件在尾矿库溃坝中的验证应用。

本文旨在预测拟建尾矿库溃坝后的尾砂流对下游的影响情况，给溃坝风险评估提供科学的依据。为了模拟溃坝对下游的影响，如影响范围或沉积厚度，本研究采用了RAMMS中的Voellmy摩擦模型进行数值计算，并且按照最危险、影响程度最大的工况进行模拟计算，即模拟尾矿坝堆积到最终高程时发生溃坝，目的是充分评估尾矿坝失稳时的最大潜在危险区和受灾范围。同时，为了验证数值模拟的准确性，利用DEM数据按1∶150的比例搭建了尾矿库的三维山体物理模型进行溃坝试验，验证数值模拟的准确性以及校验其计算参数。最后，提出尾矿库溃坝对下游环境的影响程度以及做出准确的风险评估。

1 尾矿库原型

拟建尾矿库位于福建省。尾矿库设计的最大库容量约为9.3×107m3，满堆后坝体位置在高程660～825 m。库区靠近东海，每年6—9月间台风和暴雨频繁。因此，在尾矿库建设前必须充分考虑极端降雨条件下，尾矿库溃坝对下游所能造成的破坏及最大的影响范围，对可能造成的破坏后果进行风险评估，并依此制定治理和预防事故的对策措施。

拟建尾矿库库区地形包括低丘和丘陵。总体地势西高东低。库区周围山坡坡度为25°～45°，山谷和山脊的走向是从西北到东南，山沟海拔为555～855 m。库区以砂质页岩、板岩和花岗岩为特征。尾矿库库区位于所在沟谷的最上游，下游沟谷蜿蜒曲折，自坝脚至下游3 km(时州村)之间的地形为多处山体收口与开阔地带交替的“葫芦串状”沟谷，沟底落差相对较大。下游8 km(北坑及新前排)开始，沟谷地形完全开阔，地势趋于平缓，村落分布集中。下游村落主要分布情况如图1所示，有：上地村(距尾矿坝0.7 km)，时州村(3 km)、老土楼(3.35 km)、门口庵(3.54 km)、时州水库(5.8 km)、时州水电站(7.12 km)、北坑村(7.98 km)、土楼村(9.62 km)和嵩溪镇(11 km)。

图1 尾矿库及下游村落地形(谷歌地图)

2 数值模拟及模型试验原理

2.1 数值模拟计算原理

RAMMS方法的核心是颗粒流平均深度运动方程的有效二阶数值解，可在三维模型上计算任意位置、任意时刻的流量的沉积高度和运动速度[20]。

在较大尺度工程问题上，常常是将数值计算模型与地理信息体统(geo-information system,GIS)相结合起来应用[21]。RAMMS软件首先是建立数字高程模型(DEM)，该文件是数值模拟预处理中最重要的输入数据，能够准确反映尾矿库库区的重要地形特征。DEM产生过程为：①从尾矿库区调查地貌数据中提取并转换DEM数据，得到等高线地形图；②对溃坝研究区的地形文件、三角网文件和栅格文件进行依次生成；③生成尾矿库溃坝研究区域的DEM文件。根据坝体高度、尾矿量和附近地形，结合DEM数据，建立尾矿库三维模型，如图2所示。

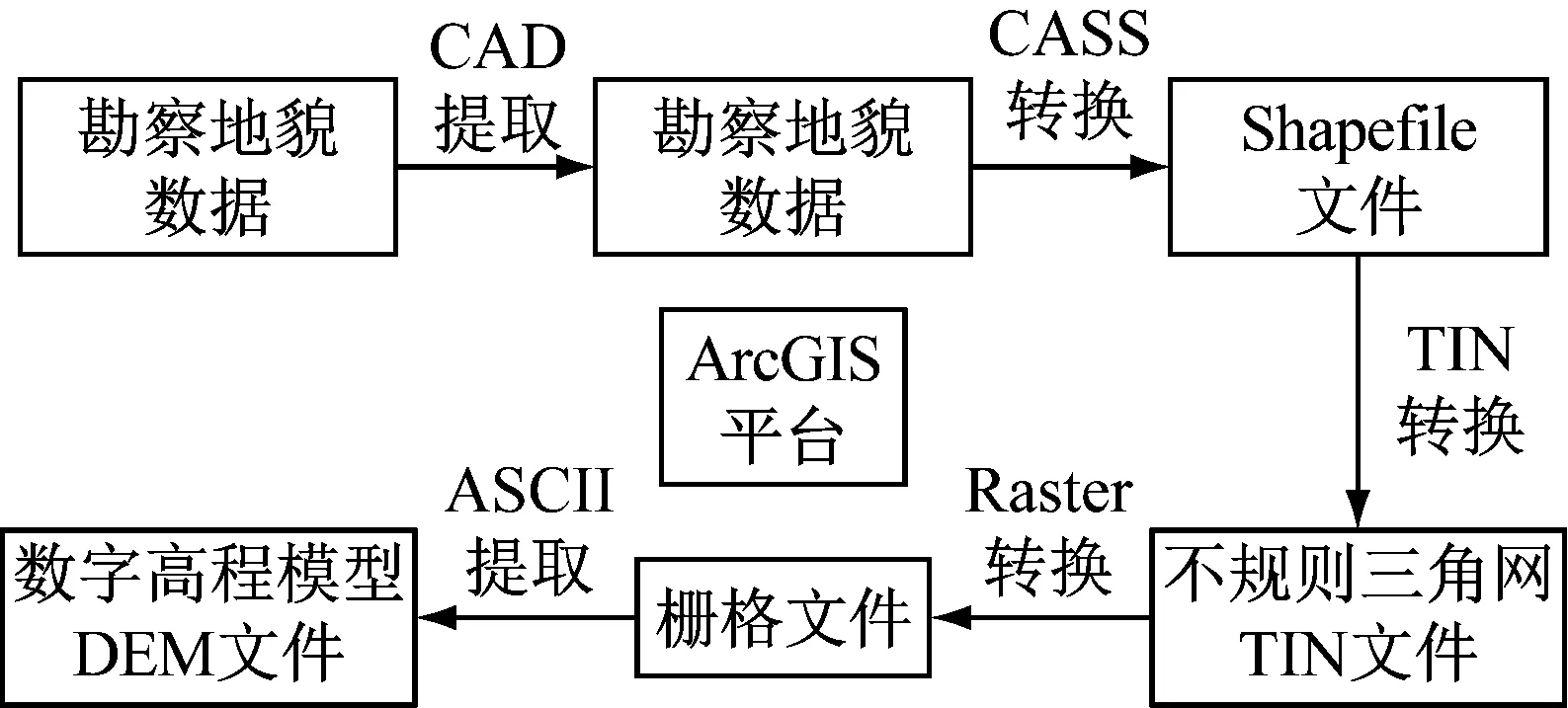
图2 勘察地貌数据的DEM生产过程

使用GIS绘图功能可指定单个或多个块体释放区域，或者通过输入水力线来指定作为时间轴的流动，或使用输入水位曲线来指定流量作为时间的函数，为用户定义模拟的信息，如流体的释放区域、流动模式和最终状态。可以在地形模型上叠加地图和遥感图像来促进模型与历史事件数据的校准(例如流速、沉积深度和流动距离)。RAMMS仿真计算中摩擦阻力的参数分为干摩擦(μ)和黏滞/湍流系数(ξ)[22]。摩擦阻力S(Pa)的计算公式为

(1)

式中：ρ为密度;g为重力加速度；尾砂运动表面的正应力N为N=ρhgcos(φ)，φ为倾斜角，h为流动高度，U=(ux,uy)T，由x方向和y方向的流速组成[23]。速度的大小关系式为

(2)

式(2)可以用质量平衡方程在Voellmy流变模型中表示为

∂tH+∂x(HUx)+∂y(HUy)=Q(x,y,t)

(3)

式中:H为流动高度；Q(x,y,t)为批量生产源项。如果Q>0，则称为夹带速率；当Q=0时，没有物质侵蚀/沉积；当Q<0时，表示沉积速率。流体的平均深度平衡方程如下

Sgx-Sfx

(4)

Sgy-Sfy

(5)

式中：Cx和Cy分别为剖面系数；gz为垂直重力加速度；Sgx=gxH,Sfx=gyH分别为x方向和y方向的驱动、重力加速度；Sfx，Sfy为驱动摩擦，重力加速度在x和y方向分别表示为

(6)

在Voellmy模型中，垂直方向上的接触关系可以定义为多相莫尔-库仑关系，其中nUx为x方向速度方向单位向量，nUy为y方向的速度方向单位矢量，ka/p为土压力系数，表示为

(7)

式中:φ为内摩擦角；Ka/p为土压力主动/被动。主动区是指膨胀流动区∇·U≥0，被动区是指压缩区域∇·U<0。此外，除了Rankine理论外，Savage等[24]还采用了其他方法来估算土压力系数。

利用上述方法可推出Voellmy流变公式为

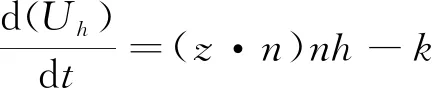
(8)

式中:变量分别用长度L、速度(gl)/2和时间(L/g)/2测量，以获得统一的流变值;k，μ′和s分别为横向土压比、有效动摩擦因数和运动方向的各向异性集合；重力矢量是z=(0,0,-1)，将扰动系数定义ζ=ξ/g为无量纲。

通过对式(8)的整理，可以得到重力岩土体黏性流动中流体内阻的计算公式为

(9)

式中:N0为流动尾矿的屈服应力；μ为一个“硬化”参数。与标准的Mohr-Coulomb类型关系不同，该公式确保当N→0时S→0，当U→0时S为0。它增加了剪切应力，从而导致尾砂流停止较早，这取决于N0的值。

2.2 物理模型试验原理及模型搭建

2.2.1 试验原理

物理模型试验已广泛应用于尾矿库溃坝规律的研究，以模拟按特定比例微缩的地貌特征下尾矿库溃坝的情况。本研究搭建了1∶150比例的试验模型，并以物理性质与原尾砂相似的炉渣为模型试验材料。模型中设计布置了梅花形渗透点，用于监测和调节尾矿库浸润线的高度，由于研究的目的是分析和预测尾矿库溃坝破坏的后果。因此需保证尾矿库的饱和度，即浸润线高度，以达到尾矿库溃坝流量。以往的研究表明，渗透溃坝试验与漫顶溃坝试验的特性相似[25]。该物理模型虽然简化了降雨入渗对尾矿库表面的侵蚀作用，以注水的方式达到漫顶的目的，对尾矿库溃坝成泥砂流过程中的发生、发展和淹没范围进行了真实的论证。同时可验证RAMMS数值模拟结果的正确性。

尾矿库物理模型试验遵循相似性准则，缩制成模型进行试验研究。以模型重演与原型相似的自然形态，进行观测，取得数据，然后按照一定的相似性准则引申于原型，以获得原型的实际现象和性质。模型和原型的物理现象保持相似所必须遵守的规则称为相似准则。模型应满足几何相似、水流运动相似和动力相似。对于研究溃坝尾砂对下游淹没影响的模型，是以淤积为主的模型，尾砂的扬动现象可以不考虑，尾砂起动相似准则也可以放宽，重点在于满足尾砂沉降相似、水流挟砂相似及冲淤变形相似3种条件[26]。

(1)尾砂沉降相似条件

根据紊动扩散理论的三元恒定均匀水流中不平衡输沙状态下的泥沙扩散方程正态模型中尾砂运动过程沿程沉降的相似条件

(10)

式中：下标ω为尾砂沉速；下标u为水流速度；下标L为长度比尺。

代入Stokes沉降速度比尺关系可得到悬移质沙粒径比尺

(11)

式中：λd为粒径比尺；γs为砂容重；γ为水容重。

(2)水流挟砂相似条件

用水流处于饱和状态时的临界含砂量来表示水流挟砂力S*。若实际含砂量S≥S*，将沿程发生淤积。水流挟砂力相似，则保证了模型与原型水流含砂量饱和与否相似。此时，水流含砂量比尺(λs)与水流挟砂能力比尺(λs*)相等，即

λs=λs*

(12)

(3)冲淤变形相似条件

由泥沙连续性方程，可得

(13)

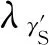
根据相似性准则，选取合格的模型砂，原型砂与模型砂的物理性质指标，如表1所示，并计算尾矿库溃坝模型在水流相似条件下的水力要素相关比尺，表2所示。

表1 原型砂与模型砂的物理性质指标

表2 物理模型试验相似比尺

2.2.2 试验模型搭建

物理模型是为了验证数值模拟的正确性，进而校核数值计算的参数，因此模型搭建范围可适当选择关键部位即可，大范围的评价及试验还需利用数值模拟，可大量节省试验时间和经费。试验尾矿库物理模型采用正态模型，建造比例为1∶150，根据野外调查和DEM数据进行搭建，模型分为六部分：山体地形模型、下游标志地物模型、水量控制系统、浸润线测量系统、水砂回收系统及监控监测系统，如图3所示。

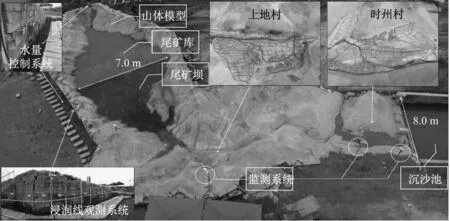
图3 物理模型设置和尺寸

模型尺寸(长×宽×高)为35.0 m×21.0 m×3.3 m，包含从尾矿库到时州村的实际影响范围。为了使得模型库内尾砂饱和，同时形成稳定的渗流，在尾矿库底部设置了水泵和压力计等系统和浸润线控制和测量系统，可对尾矿库的入渗压力和渗入量进行测量并能控制浸润线的高度，并利用一系列的实时监测设备和分析软件收集尾砂流的波形和速度等数据。

在尾矿库物理模型中，通过埋入水位监测仪和流量监测点观测浸润线的变化规律(见图3(b)和图3(c))。采用RIEGL型三维激光扫描仪(3DLS)、无人机(UAV)、5KF20型高清摄像系统(HDCS)对尾矿库溃坝位移变化进行监测；利用表面流场实时测量系统(VDMS-LAB-04C型)监测溃口流量变化和流量峰值过程。尾矿库溃坝监测系统布置图，如图4所示。

图4 流场监测系统的布置

3 计算及试验结果

3.1 溃坝尾砂流演进结果

3.1.1 数值模拟结果

RAMMS模拟与物理模型均是使用笛卡尔坐标系作为数字高程模型快速捕获地形的数据，如图5(a)所示。基于Voellmy-Fluid方法，采用无通道尾砂流进尾砂流模拟，将尾矿库深度、高程和平均坡角定义为RAMMS释放区域的初始参考信息。由图5(b)可知，浅灰色“L”形区域为包含关键地形信息的计算区域，深灰色区域为溃坝运动的释放区域，其高度为54 m，体积为1.74×107m3。当各节点元素的动量均小于最大值的5%时，仿真停止。

(a) 尾矿库DEM模型

RAMMS碎屑流动态分析软件基于Voellmy流动摩擦理论，假定碎屑流是单向模型，将所有的尾砂作为一个整体，无法区分出固相和液相物质，摩擦阻力由干摩擦参数(μ)和黏滞/湍流型参数(ξ)控制[27]。因此模拟RAMMS模拟尾矿库溃坝最大的难点在于漫顶溃坝过程中尾矿碎屑流的成分十分复杂，摩擦参数的选择对结果影响明显。模型试验选择与原型砂力学性质相似、造价低、容重适中的火电厂炉渣作为模型砂。通过现场测量，结合流槽试验及溃坝模型试验中尾砂流的流量流速变化，考虑尾砂流的流动路径和分布，最终确定RAMMS数值模拟的摩擦参数为μ=0.07，ξ=1 700。根据Voellmy方法的内存大小和计算效率，最终生成1 334 514个计算机流量单元和1 338 190个流体节点。通过多次物理模型预备试验，校验后的RAMMS数值仿真模拟参数,如表3所示。

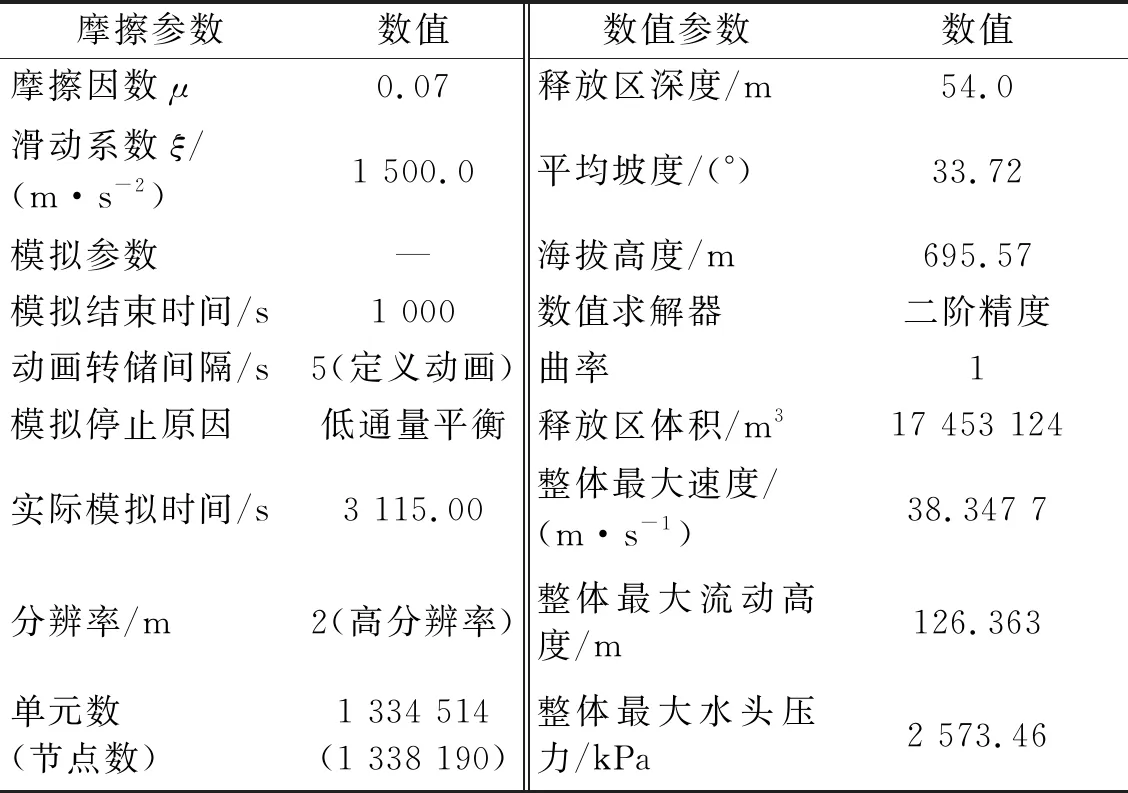
表3 模拟计算参数设置及主要计算结果

利用上述方法，对拟建尾矿库研究区的潜在失效为出发点进行了建模和计算。RAMMS数值结果如图6所示，RAMMS模拟仿真计算的溃坝进程描述如表4所示。

表4 RAMMS模拟仿真计算的溃坝进程

(a) t=30 s

3.1.2 物理模型试验结果

试验工况为洪水漫顶导致尾矿坝溃坝，该工况下尾矿库库区水位处于临界状态即最高洪水位，此时干滩长度0.67 m(相对应原型100 m)，在该状态下遭遇洪水最终导致漫顶溃坝发生。本次溃坝模型具有落差显著，势能大的特点，溃坝后库内存水急流直冲而下，可挟带走大量的尾砂。溃坝尾砂流具体的演进情况如图7所示，演进的进程描述如表4所示。

(a) t=45 s

模型试验溃坝进程以及溃坝尾砂流对下游村庄影响的进程如表5所示，其中监测时间为从尾砂流到达坝脚时起算。相对应的原型时间依据时间比尺进行换算(见表1)。

表5 模型试验溃坝尾砂流进程

物理模型试验中尾沙总体的溃泄量是采用RIEGL型三维激光扫描仪(3DLS)进行扫描测量,如图8所示。测得影响范围为0.558 km2，总溃泄量为1.3×107m3，与RAMMS统计的倾泻量1.33×107m3对比，二者误差仅为2.3%。

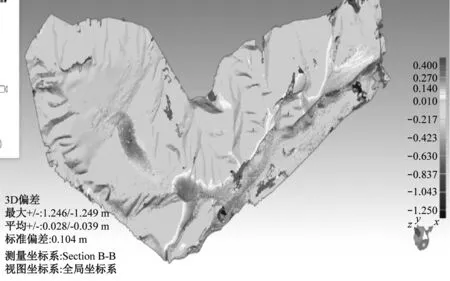
(a) 溃坝模型中泥砂沉积厚度

在物理模拟试验中，大坝溃坝和随之而来的尾砂流发展速度很快。水的注入使得水位上升和尾矿库坍塌导致矿浆快速移动和膨胀[28]，尾矿坝上的这种快速破坏和泥浆的发展，也体现在了物理模型试验中决口和浆液的发育是由极端降雨和水分渗透引起的[29]。

从两者的溃坝进程来看，总体的演进规律相仿，总体的溃泄影响范围以及溃泄的尾砂量基本一致，存在的差异是在时间节点上。数值仿真模拟计算实现溃泄的方法是设置一个滑坡体下滑过程，而物理模型试验溃坝的所形成的尾砂流是洪水漫顶冲刷的发展过程，故此存在差异，但不影响试验结果的准确性，所以在获取溃泄冲刷的时间时，应以物理模型试验数据为准，更符合实际的情况。

3.2 淹没深度与溃泄量对比

为测量溃坝尾砂流沿下游的淹没范围和淹没深度，将研究区5个关键位置的淹没深度与模型试验结果进行了对比,如图9所示。

(a) 模型试验测量截面

在尾矿库库区下游关键位置设置监测断面，采用模型试验实际测量和数值模拟结果分析，对比各监测断面的尾矿碎屑流的最终流动高度、流量随时间的变化过程及最终截面处的流量大小。通过模型试验与数值模拟结果对比分析可知，1#、4#、5#截面处的尾砂流动高度基本一致，上地村区域(2#、3#截面)的尾砂流动高度差别较大，分析是与尾砂的密度有关，模型试验为了使坝体发生失稳破坏，短时间内持续给库区加水，会导致尾矿库在极短的时间内浸润线高度升高，导致库区大部分尾砂趋于饱和，但少部分尾砂依然处于非饱和状态，坝体内部碎屑流的密度及饱和度分布与实际情况略有不同，但不影响试验结果的准确性。为了下游社区和居民的安全，在风险评估中应以两者之间的最大值为建议值，对拟建尾矿库进行安全评价。

将RAMMS数值模拟结果与模型试验进行对比发现，两种分析过程相辅相成，相互验证,如表6所示。两种研究方案在尾矿库溃坝动态分析过程中优势互补，互相验证。两者试验结果与单一方法相比更准确深入，能够更全面的分析尾矿库溃坝碎屑流的演进及致灾影响问题。

表6 模型试验与数值模拟结果对比表

4 结 论

本研究采用RAMMS数值模拟计算方法和物理模型试验手段，仿真模拟了拟建尾矿库在最终坝高时发生溃坝后尾砂流在下游地形上的运动规律。经过模型试验与数值计算结果的相互对比与印证，获得了尾矿库溃坝破坏时尾砂流的演变进程和潜在的影响范围等数据。本次尾矿库溃坝的仿真模拟对工程实践具有很强的指导意义，同时在试验过程中也获得了一些研究经验。

(1) 研究得出拟建尾矿库如在最终坝高时发生溃坝，9 min尾砂流开始冲击距坝脚下游0.7 km处的村庄，18 min将对村庄造成全面淹没，最终影响范围约为0.558 km2，尾砂的溃泄总量可达1.3×107m3。试验结果说明溃坝危害大且基本不具备预警时间，同时结合潜在的危险范围，建议在尾矿库的设计、管理和风险评估过程中，合理的增加防灾减灾的措施。

(2) 通过模型试验和数值计算的对比，尾砂流溃泄总量二者误差仅为2.3%，沿线淹没深度基本一致，说明经模型试验参数校验后的RAMMS计算结果是可靠且有效的。溃坝模型试验成本昂贵、耗时长、难度大且模拟的范围有限，利用参数校验后的RAMMS方法则能弥补这些缺陷，同时说明该研究方法能较好地解决尾矿库溃坝尾砂流穿越真实地形的演进问题。

(3) 尾矿库溃坝模型试验复杂繁琐且难于操控，本次试验中发现主要影响因素有——地形模型的精确程度、模型砂的相似程度、模型堆砂与原型排砂贴近程度等。本研究中物理模型与数值建模采用相同DEM基础数据，保证了地形边界条件的一致性；结合溃坝泥砂流运动特性选择沉降、水流挟砂和冲淤变形3个关键相似条件，确保选配的模型砂运动规律最相似于原型砂；实际库内排砂是长期的沉积过程，通过调节模型堆砂压实度满足与原型相似的力学性质，最大程度贴近于原型排砂。