新型竖向电涡流-磁力混合阻尼装置试验研究

2022-02-22朱前坤马齐飞杜永峰

振动与冲击 2022年3期

朱前坤, 马齐飞, 张琼, 杜永峰

(兰州理工大学防震减灾研究所，兰州 730050)

随着城市化的迈进和建筑行业的飞速发展，出现了大量轻质、柔性结构[1]。这些结构，具有阻尼低，频率低等特点[2]。一旦激励荷载的频率和结构接近，会发生共振，产生较大响应，严重时还会造成结构破坏，危害人身和财产安全[3]。为解决此类问题，最常用的措施是对结构进行被动控制[4]。

被动控制中以调谐质量阻尼器(tuned mass damper,TMD)减振控制备受青睐。常用的阻尼器有橡胶阻尼器[5]，液体黏滞阻尼器[6]和电涡流阻尼器[7]等。其中橡胶阻尼缺点是容易老化[8]；液体黏滞阻尼器不易养护，且会有漏油现象[9]；电涡流阻尼器因刚度和阻尼可分离而备受关注[10]。

TMD减振原理是结构受到外力作用发生振动带动TMD运动，TMD运动过程中对结构施加一个反向的惯性力，以此控制结构的振动[11]。现在国内外学者已经对电涡流阻尼器进行了大量研究：其中Lee等[12]采用近似理论对涡流制动控制器模型进行了分析，并通过试验得出涡流阻尼力与速度成正比的结论。汪志昊等[13]提出了一种电涡流TMD构造与磁路优化设计的方法，通过有限元仿真和试验确定其最优间距、运动方向、相邻永磁体磁极宜同向布置。Kwak等[14]通过在悬臂梁的末端连接一个柔性结构、两个永磁体和固定铜板，永磁体运动改变穿过铜板的磁通量，产生电涡流。Sodano等[15]通过在导体板外侧放置第二个磁性相反的磁铁来压缩磁场，从而提高磁通量来提高阻尼力。而实际应用中电涡流阻尼器存在漏磁现象，最优阻尼比也很难达到，有时仅用一种阻尼形式很难达到最佳控制效果。需要引入一种新的阻尼与电涡流阻尼进行混合减振。磁力在减振应用中研究颇多：Sebastian[16]提出了一种新型的旋转对称磁力阻尼器，并通过试验证明这种磁阻尼器对风力涡轮机上的振动有较好的减振控制效果。Fune等[17]利用两个磁性橡胶层制作了磁力减振器，其原理是由滑动摩擦产生的这种摩擦损失与由磁性橡胶层变形产生的内部损耗同时作用,因此减振效果非常显著。汪志昊等[18]提出了一种基于永磁体作用力的频率调节方法，通过调整永磁体相互作用力带来的附加刚度调节摆式调谐质量阻尼器的频率。李辉等[19]提出了一种磁悬浮减振器的设计方案，磁悬浮减振器的弹性介质是两块同极相对的高强度永久磁铁，分析比较表明，它的综合性能优于螺旋弹簧。Zhou等[20]用梁弹簧与由电磁体和永磁体构成的磁性弹簧并联，进行了被动、半主动控制，结果表明该装置控制效果显著。上述学者所研究的并联磁铁将提供负刚度，且磁力减振技术大多应用于车辆减振中，在土木工程领域鲜有所闻。

本文提出了一种电涡流-磁力阻尼器(eddy current-magnetically tuned Mass damper,EMTMD)。首先介绍了EMTMD的减振原理及其对结构减振控制的运动方程。接着介绍了EMTMD的设计方法，并提出了一种磁力附加刚度和等效磁力阻尼系数的计算方法。然后对不同磁路设计的EMTMD进行试验，测量自身的动力参数。最后用其对结构模型进行减振控制，计算出各个工况下的减振率，进而得出EMTMD不同工况对结构振动控制效果的不同影响。

1 减振原理及振动方程

1.1 EMTMD的工作原理

电涡流-磁力阻尼系统是由永磁铁和导体板组成的电涡流阻尼系统和两组相对磁铁组成的磁力阻尼系统构成，如图1所示。其耗能原理主要为涡流损耗和磁滞损耗两种。涡流损耗是导体板在磁场中做切割磁感线运动，磁通量改变形成电涡流，发热耗散振动的能量[21]。磁滞损耗是铁磁体等在反复磁化过程中因磁滞现象而消耗的能量，这部分能量转化为热能，以此耗散振动的能量[22]，因而达到结构振动控制的目的。

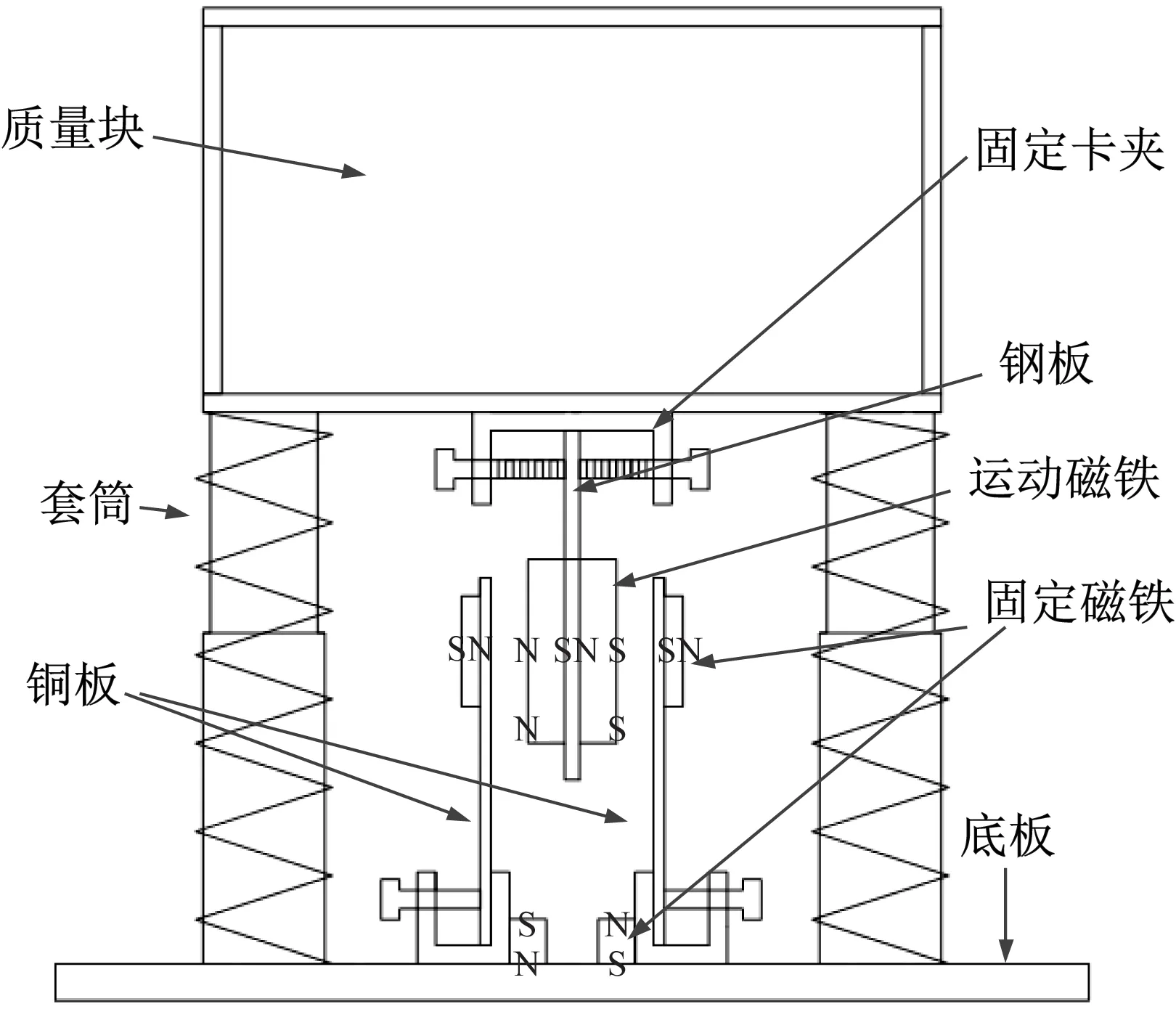
图1 EMTMD设计样机图

1.2 结构振动分析模型

竖向结构受到激励时，会产生竖向振动。竖向阻尼器控制竖向振动时，可将全部质量集中成单点。磁力可增加EMTMD的附加刚度[23]。竖向EMTMD的简化计算模型如图2所示。

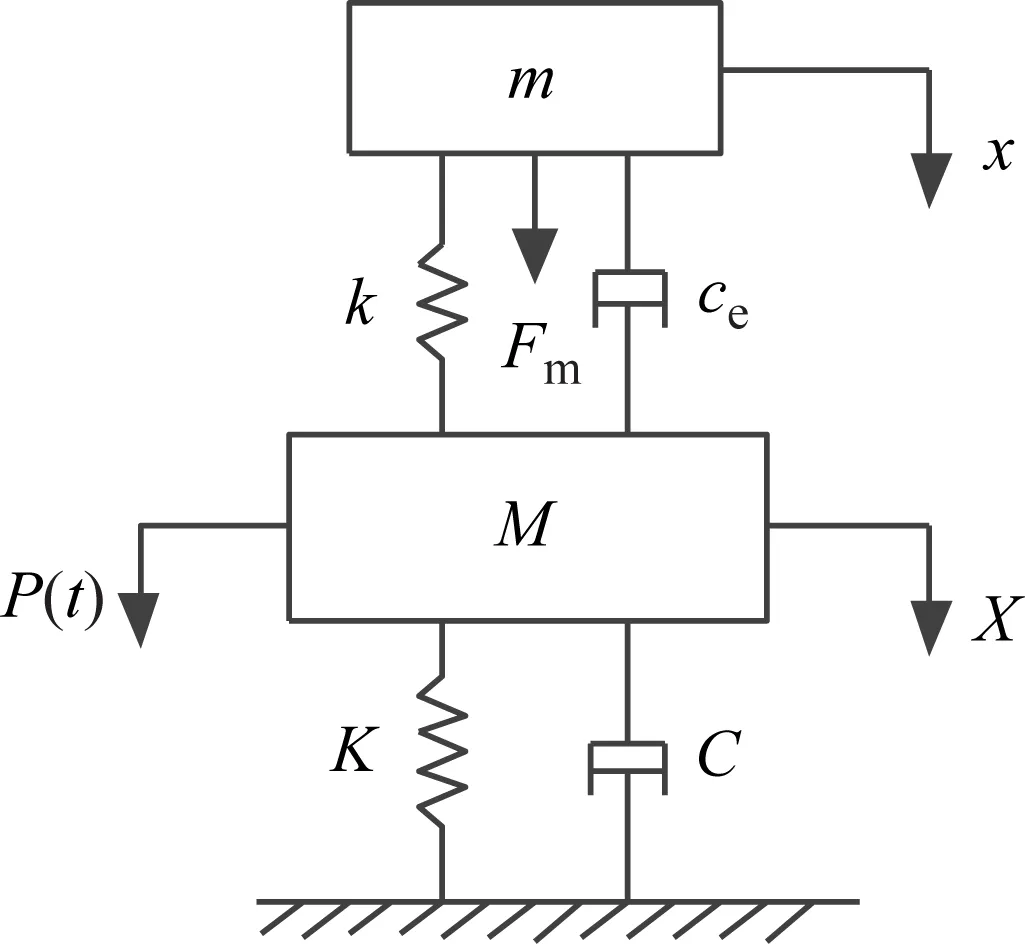
图2 EMTMD控制结构的计算模型

图2中：M为主结构的质量；K为主结构的刚度；C为主结构的阻尼系数；X为主结构的响应位移；m为EMTMD装置的质量；k为EMTMD装置的刚度；ce为EMTMD装置的阻尼系数；x为EMTMD装置的响应位移；Fm为磁铁磁力;P(t)为外部激励荷载。

特定磁路设计的磁力给EMTMD提供负刚度，其定义为在外部荷载变化量与变形变化量方向相反的情况下，刚度为负刚度[24]，对结构和EMTMD列运动平衡方程如下

(1)

式中：km为结构的附加刚度；C1为装EMTMD装置系统的总阻尼系数，C1=C+ce。文献[25]也将磁铁等效为弹簧，故本文定义km为附加刚度。故定义磁力Fmsinθ=km(x-X)，代入式(1)

(2)

其中两磁铁间磁力简化公式[26]为

Fm=(Bg/4 965)2Ag

(3)

式中：Bg为磁感应强度，Gs(1 Gs=1×10-4T);Ag为磁极面积。

永磁体为长方体的一对平行吸力型永磁体间隙中点磁感应强度为[27]

(4)

式中：Br为永磁体剩磁感应强度；Lm为永磁体高度；h为一对永磁体间隙；a为磁铁长度；b为磁铁宽度。其中[28]

Br=μ0·Jm

(5)

式中：μ0为真空磁导率；Jm为永磁体束缚面的电流密度。

2 EMTMD的设计

2.1 结构模型的动力特性

本次选用试验室的结构模型为试验对象，如图3所示。结构模型长为10 m，宽为1.6 m。由5块2.0 m×1.6 m的双层夹胶钢化玻璃(厚25 mm)组成桥面，粘接在由两根10 m的25a型工字钢和6根1.6 m的25a型工字钢焊接形成钢框架主体上。钢框架搭接在支座上，支座采用地脚螺栓锚固连接在地面。

图3 结构模型图

本文中只控制结构模型的竖向振动。测得该结构模型静载下前三阶的自振频率分别为4.14 Hz，6.20 Hz和15.50 Hz，结构一阶模态质量m1=795 kg。结构模型发生竖向振动时，中间位置振动最为剧烈[29]，如图4所示，为一阶振型位移峰值处。因此EMTMD需要安装中间位置控制结构模型的竖向一阶振动。

图4 结构模型的第一阶竖向振型图

为探究EMTMD对结构模型振动控制的效果，首先必须确保激励的一致性。本试验选用APS400激振器，质量为75 kg，占一阶模态质量的9.4%。考虑激振器的质量对结构模型一阶频率的影响，将其放入结构跨中，测得竖向一阶频率为4 Hz，激振器自质量使结构一阶频率下降0.14 Hz。然后根据结构模型的动力特性，确定EMTMD的设计参数。

2.2 EMTMD的参数设计

EMTMD的特色在于在铜板后或者底板上安装磁铁，该磁铁和质量块运动磁铁磁心相对，相斥或相吸。增加磁铁，会改变阻尼器的刚度和频率。为此提出了一种假设试验法来确定EMTMD的参数，即先根据电涡流阻尼器的要求进行参数设计，然后增加磁铁之后通过改变质量调节频率即可提高阻尼器的鲁棒性。

设计TMD需先确定其有效质量与结构模态质量之比μ。通常μ越大，对结构振动控制效果越好。但受成本和安装空间等因素制约，质量比一般取1%～5%[30]，本文μ取2%，则TMD运动质量为15.9 kg，振动频率为4 Hz。由文献[31]可知

(6)

(7)

md=μm1

(8)

式中：μ为TMD质量与结构模态质量的质量比；fopt为TMD与结构模态的最优频率比；kopt为TMD的刚度；md为TMD的质量；copt为TMD的阻尼系数；ω1为结构的一阶圆频率；m1为结构的一阶模态质量。

2.3 刚度构件

TMD应配备严格的导向系统，它产生的摩擦阻尼要尽量小[32]。因此本文通过无摩擦且导向性能好的4个直线套筒结构进行导向，选用4根螺旋压簧。单根弹簧的刚度系数即为2.411 kN/m，螺旋弹簧的刚度计算式[33]

(9)

式中:G为弹簧钢的剪切模量；D为弹簧的中径；n为弹簧的有效圈数；d为弹簧丝的线径。

计算得到各参数如表1所示。为了提高稳定性，选用的压簧中径应适当加大，故弹簧刚度会略微增加。表1对应的弹簧刚度系数为2.85 kN/m。

表1 压簧的设计参数

2.4 电涡流-磁力阻尼构件设计

依据EMTMD的工作原理，分别设计电涡流阻尼元件和磁力阻尼元件。中指出电涡流TMD受到的电涡流阻尼力与其速度的比值即为电涡流阻尼系数。对于电涡流阻尼元件设计，电涡流阻尼系数简化公式[34]

ce=σδSB2

(10)

式中：σ为导体板的导电系数；δ与S分别为导体板的厚度与有效表面积；B为导体板表面主磁感应强度的大小。

由式(9)可知，在同等条件下，导体板的厚度、导电系数、内外主磁感应强度的平方和电涡流阻尼的大小成正比。而磁场强度的大小又与永磁体磁性的强弱及磁路的设计密切相关。钕铁硼(NdFeB)是目前性价比最高的磁铁，磁性极高。试验采用N35牌号NdFeB矩形永磁体，其主要参数有：剩磁感应强度1.2 T；最大磁能积为2.8×105Jm-3；矫顽力与内禀矫顽力分别为8.7×105A/m、9.6×105A/m；长(a)×宽(b)×高(h)分别为50 mm×30 mm×10 mm。导体板选用导电系数较高的紫铜，电导率为σ=5.8×107S/m。铜板尺寸为100 mm×100 mm×6 mm,距离磁铁9 mm处用高斯计测量得到磁通量为0.162 T，由此计算出单块永磁体阻尼系数为13.64 N·S/m。由于磁力也将提供阻尼，对其研究较少，阻尼系数尚没有完善的理论公式用于计算。为避免过阻尼对试验结果造成的影响，保守计算，仅选取两块永磁体，其对应电涡流阻尼系数为27.28N·S/m。然后安装磁力阻尼元件。根据磁铁的安装位置，设计了3种电涡流-磁力阻尼器如表2所示。选取第3种磁路设计如图1所示。

表2 EMTMD磁路设计

假设安装磁力阻尼元件后，质量块和弹簧刚度不变，振动频率以结构的一阶频率f1计算。先测量EMTMD的自由衰减曲线，经过傅里叶变换得到自振频率f，则EMTMD的刚度公式为

k=(2πf)2md

(11)

式中，k为EMTMD的总刚度。由于弹簧和等效磁力弹簧是并联，故磁力提供的附加刚度为

km=k-ks

(12)

EMTMD的质量计算公式

(13)

然后测量得到无阻尼系统时TMD的固有阻尼比，阻尼系数计算公式[35]

c0=2mmω0ζ0

(14)

式中：ω0为TMD固有圆频率；ζ0为TMD未安装阻尼原件的固有阻尼比。

EMTMD运动过程中，磁滞损耗耗能，磁力也会提高EMTMD自身阻尼比。由磁铁产生的阻尼系数称为等效磁力阻尼系数。因此EMTMD运动过程中受到的阻尼分别来自电涡流阻尼、磁力阻尼、TMD无任何耗能原件时的固有阻尼。因此EMTMD总的阻尼系数即为三者之和。故c0+cm+ce=2mmωmζ，所以EMTMD的磁力阻尼系数试验值为

cm=2mωmζ-c0-ce

(15)

式中：ωm为EMTMD固有圆频率；ζ为安装电涡流-磁力阻尼系统TMD的阻尼比。

2.5 竖向EMTMD的制作

根据EMTMD的参数设计，制作了可调质量的竖向EMTMD样机。质量块由6块钢板焊接形成的长方体空腔和填充的沙子组成，钢板质量为11 kg，可调节质量为7 kg，如图5所示。质量块与底板通过套筒连接。质量块和底板通过4对内径不同的钢管形成套筒，安装在4个弹簧上，弹簧承受质量块的全部质量。磁铁安装在钢板上用卡夹夹在质量块底部，随质量块一起运动。底板上安装U型卡夹固定导体板。

图5 EMTMD样机

3 EMTMD性能测试与分析

将制作的EMTMD样机进行试验，首先进行其自身阻尼比的测量。测量阻尼比常用方法有[36]：半功率点法；自由衰减法；共振频率法；放大系数法。本文选用自由衰减法测量EMTMD的阻尼比。

3.1 EMTMD阻尼比测定

EMTMD的频率和结构自振频率相近时，对结构能起到较好的控制效果[37]。因此首先通过试验来调节TMD的频率。将阻尼器质量块按压到可运动的最大位移处，释放使其自由衰减。测得的加速度时程衰减曲线经过傅里叶变换得到自振频率。通过改变质量直至频率调节为4 Hz，然后计算阻尼比。通过多次试验，最终调节质量块质量为17.38 kg，此时固有频率为4.069 Hz。

电涡流TMD计算阻尼系数时需要测量磁铁到导体板的磁通量。考虑到可能会有漏磁现象发生，因此保守测量，即分别用高斯计测量磁铁上3个点(a/2，b/2)(a/2，0)(0，b/2)到导体板的平均磁通量B值来计算，如见表2。电涡流TMD的理论预测阻尼比计算公式为[38]

(16)

式中：md为TMD的运动质量；ω0为TMD的圆频率。通过式(16)计算电涡流阻尼器阻尼比为3.06%，由于实物存在漏磁的现象，试验值将小于计算值。因此在EMTMD阻尼系数计算过程中，为避免电涡流阻尼系数计算值过于偏大，计算值应乘以缩小系数。定义缩小系数=电涡流阻尼器测量阻尼比/电涡流阻尼器理论预测阻尼比。

由于磁力TMD的相关研究较少，因此EMTMD-2、MTMD-3仅测量距上下磁铁表面1 mm处和中间位置的磁通量作为参考。为避免质量比不同，本文质量取统一，然后测试磁铁对EMTMD自身的影响。根据磁铁的尺寸对其进行编号为10 mm×10 mm×5 mm(1)、20 mm×10 mm×5 mm(2)、30 mm×10 mm×5 mm(3)、20 mm×20 mm×5 mm(4)、40 mm×20 mm×5 mm(5)、20 mm×10 mm×10 mm(6)、20 mm×20 mm×10 mm(7)、30 mm×10 mm×10 mm(8)、30 mm×20 mm×10 mm(9)、40 mm×20 mm×10 mm(10)10组。现有研究中并联磁铁提供负刚度会有很好的减振效果，故本研究提供正刚度的仅选取一组作为对照。试验测得磁铁吸力对EMTMD-1提供正刚度，斥力对EMTMD-2提供正刚度。故EMTMD-1磁铁选用编号为2，吸力仅一组。而磁铁斥力的磁路设计提供负刚度，分别选用编号：1、2、3、4、5、6、8、9、10。EMTMD-2磁铁选用编号为10，斥力仅一组。磁铁斥力的磁路设计分别选用编号： 3、6、7、8、9、10。对于EMTMD-3为方便寻找最优磁路设计，先确定EMTMD-2对电涡流影响较小，且减振性能提升最高的底板磁铁，然后控制铜板后磁铁的尺寸为变量来对比每种组合的减振率。在此底板吸力磁铁暂定为编号9，铜板后斥力磁铁编号为1、2、4、7、8。后续将根据EMTMD-1和EMTMD-2对结构的振动控制效果做出适当调整。

经过试验测得安装不同磁铁的3种EMTMD的频率和阻尼比。试验结果如表3所示(表3中数据均已减去TMD自身阻尼比0.8%)。

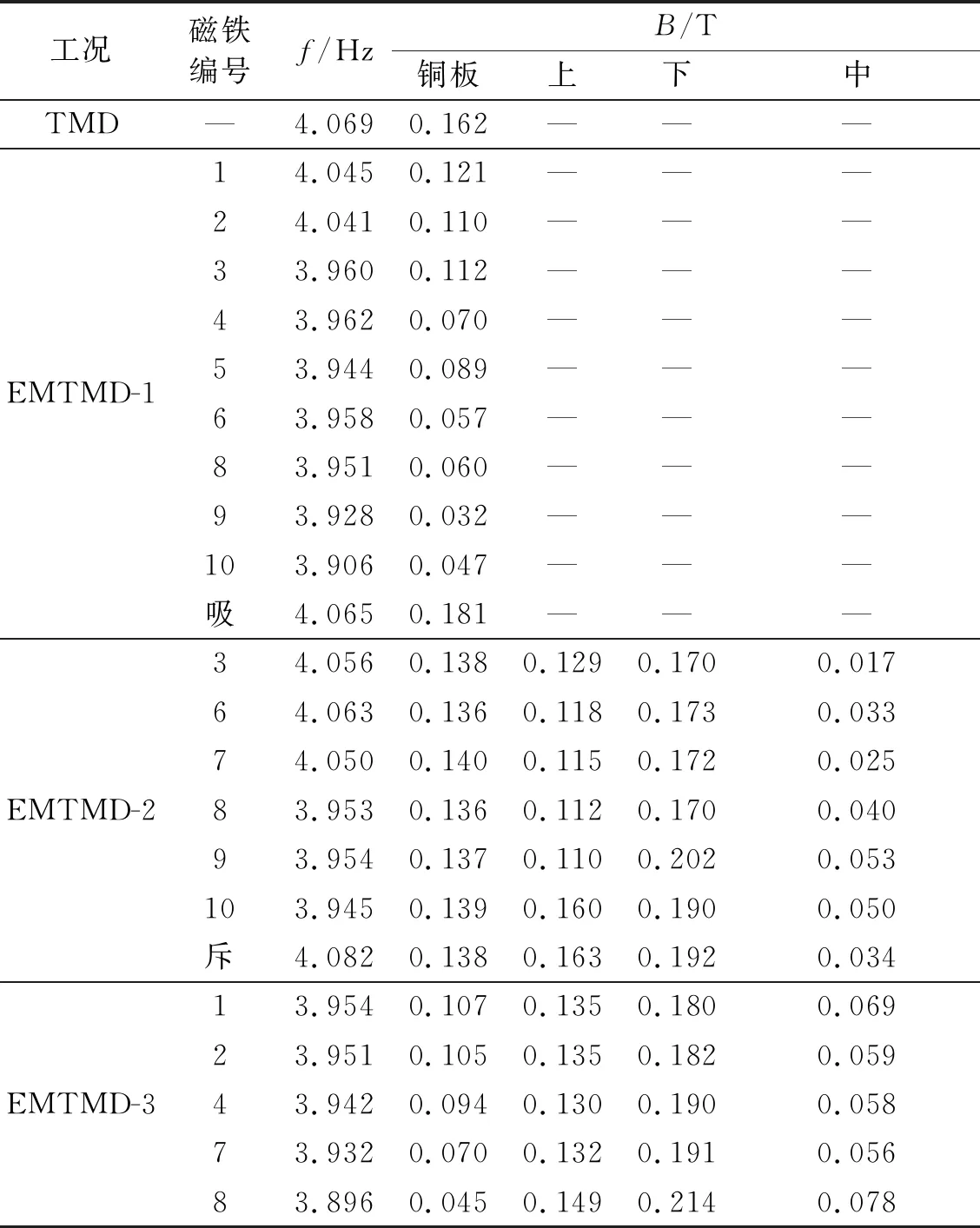
表3 不同磁铁下EMTMD参数测量及计算

通过表3数据分别用式(16)、式(10)、式(15)算出结构阻尼系数、电涡流阻尼系数、等效磁力阻尼系数。具体如图6所示。

由表3和图6可知：EMTMD-1是吸力、EMTMD-2是斥力的磁路设计，能增加自身的正刚度，从而增加频率；EMTMD-1是斥力、 EMTMD-2是吸力的磁路设计，会增加自身的负刚度，从而减少频率。EMTMD-1的电涡流阻尼系数和磁力阻尼系数由编号1的17.14N·S/m和4.59 N·S/m，到编号10的2.58 N·S/m和26.49 N·S/m，说明斥力能减少电涡流阻尼系数，增大等效磁力阻尼系数；EMTMD-2的电涡流阻尼系数和磁力阻尼系数由编号3的16.72 N·S/m和5.98N·S/m，到编号10的16.96 N·S/m和4.84 N·S/m，说明电涡流阻尼系数和等效磁力阻尼系数比较稳定；EMTMD-3的电涡流阻尼系数和磁力阻尼系数由编号1的10.05 N·S/m和12.37 N·S/m，到编号9的1.78 N·S/m和32.89 N·S/m，说明底板磁铁一定，增加铜板后磁铁的表面积或厚度，都会降低频率，降低电涡流阻尼系数，提高等效磁力阻尼系数。

为了更直观的表现频率和负刚度的关系，由式(11)计算出磁力附加刚度，并将数据绘如图7所示。

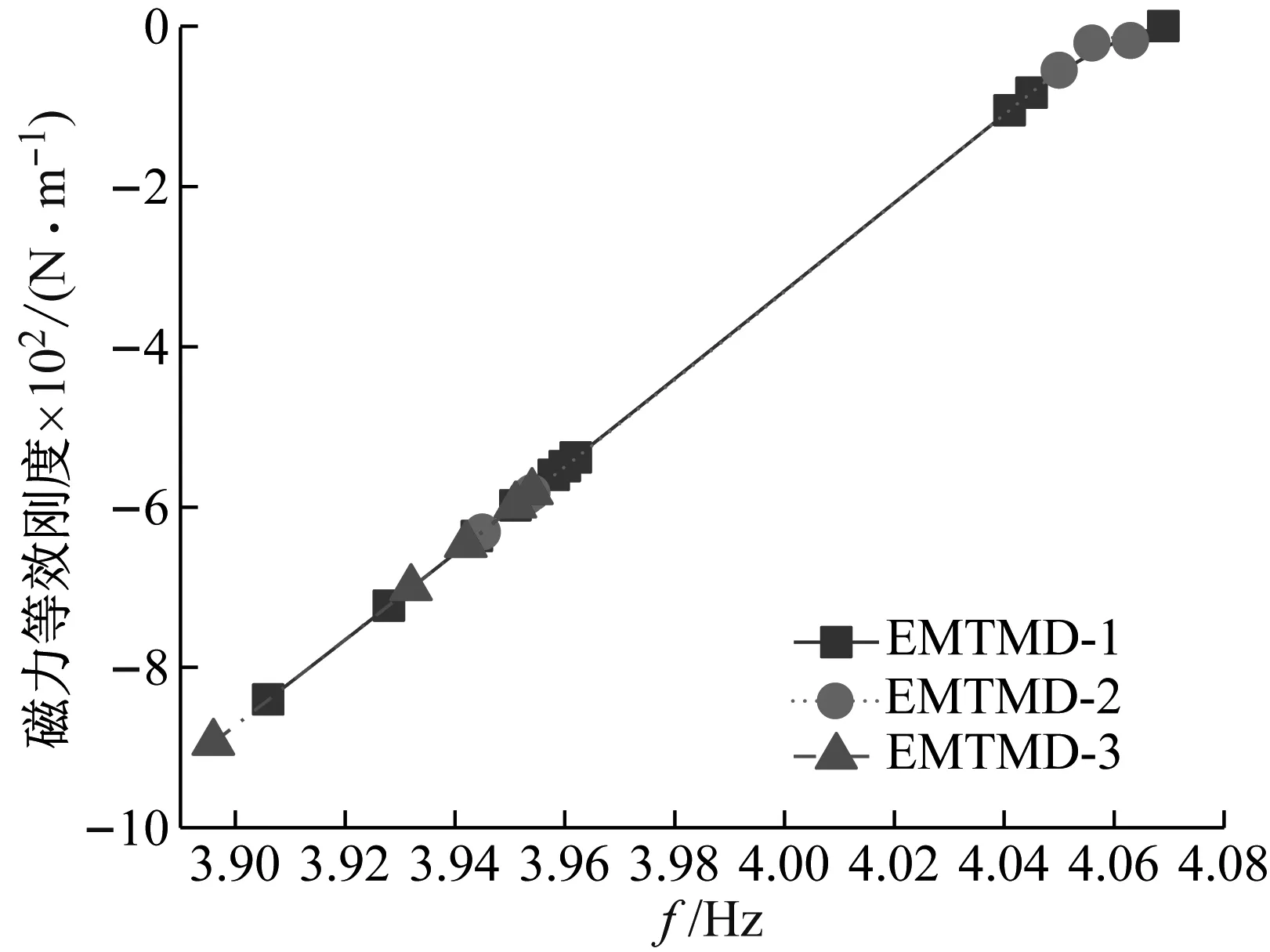
图7 EMTMD的频率和负刚度变化曲线

由图7可知，EMTMD-1、EMTMD-2、EMTMD-3的频率变化分别由4.045 Hz到3.096 Hz；4.056 Hz到3.945 Hz；3.954 Hz到3.896 Hz。对应的附加刚度变化分别为-83 kN/m到-840 kN/m；-21 kN/m到-631 kN/m；-581 kN/m到-894 kN/m。频率和刚度几乎为线性关系。由此表明，增加磁铁使EMTMD频率降低，而EMTMD的负刚度随着频率的降低呈线性增长。为研究电涡流-磁力阻尼器增加负刚度对结构振动控制效果的影响，需将其放在结构上进行试验。

4 EMTMD对结构模型的振动控制

为研究EMTMD对结构的减振控制效果，将其应用于结构模型上进行振动控制。试验装置如图8所示。选用APS400激振器进行激励，结构的位移用Banner-250U激光位移计测量，结构模型的加速度用941B拾振器测量。用DG1022U信号发生器输入激励频率和激励幅值，经过AP145放大器传输到APS400激振器进行激励。采集系统选用DH-5921应变采集仪和INV3060 V采集仪分别采集位移信号和加速度信号。

(a) 测量仪器位置图

将激振器放置结构跨中，首先以4 Hz正弦激励对结构模型进行激励。测量得到加速度时程，通过快速傅里叶变换得到结构模型的振动频率如图9所示。

图9 激振器4 Hz激励下结构的加速度傅里叶变换图

由图9可知，结构模型的竖向振动频率主要以4 Hz、20 Hz、24 Hz、28 Hz为主。值得指出的是，并不是当TMD频率比严格等于1时，TMD的控制效果最佳，当TMD频率比近似为1时，控制效果已可满足工程需要[39]。本文设计的TMD仅对结构竖向一阶频率进行减振控制，磁力对频率影响较小，且阻尼器频率都在4 Hz左右，故为避免质量比不同带来的影响，质量将不再改变。

4.1 安装磁铁为吸力或斥力的EMTMD对结构模型振动控制的影响

为探究安装磁铁为吸力或斥力的EMTMD对结构模型振动控制的影响，将EMTMD安装在结构的中间位置进行振动控制。首先测量未安装EMTMD结构模型的位移和加速度，即让信号发生器输出激励频率4 Hz，激励幅值10 VPP使激振器激励结构模型，发生共振，且每次输入激励保持一致。用拾振器测量结构中间位置的加速度；用激光位移计测量结构模型的位移，如图10所示。然后安装电涡流TMD，安装磁铁为吸力或斥力的EMTMD对结构模型进行减振控制。测量的加速度和位移时程曲线图如11所示(仅选取EMTMD-1其中一组)。

图10 结构模型振动控制试验现场照片

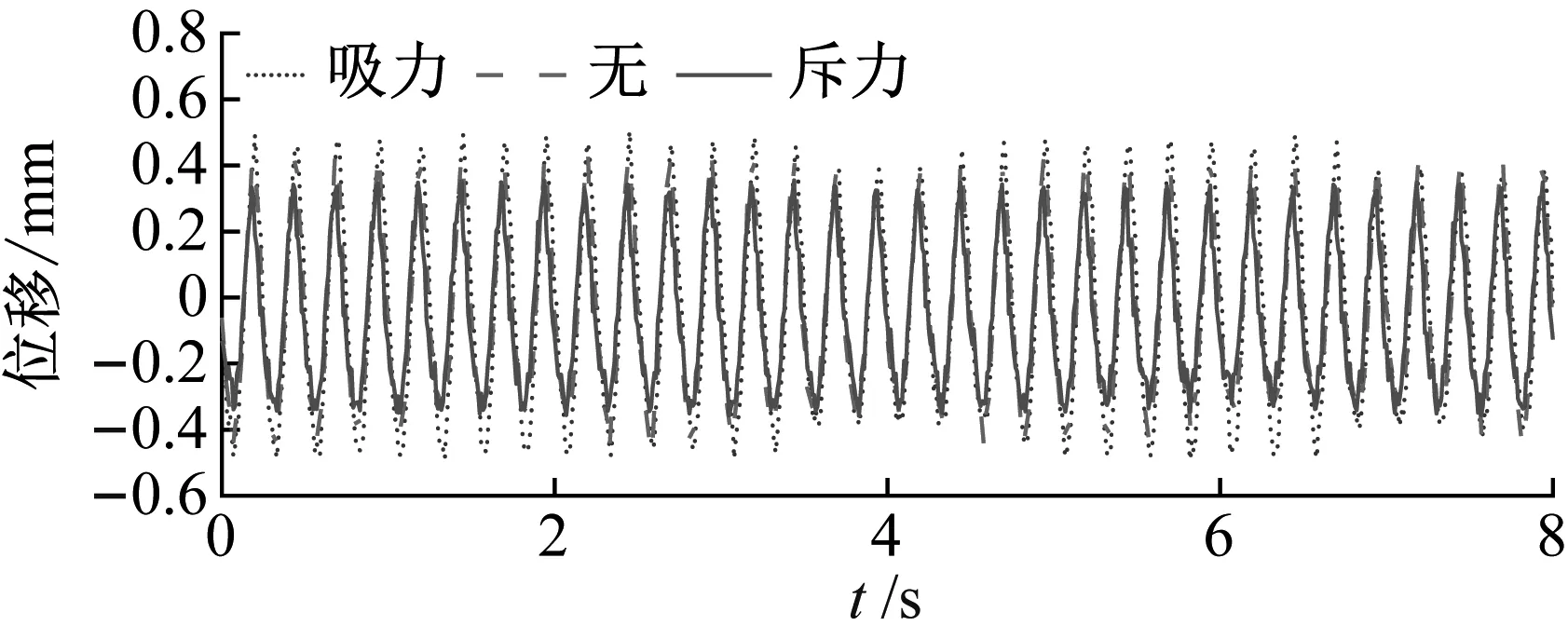
(a) 位移时程曲线

试验测得结构模型未安装阻尼器时在该激励荷载作用下位移和加速度峰值分别为8.11 mm和0.236 81 m/s2。由图10可知，结构模型安装电涡流阻尼器，EMTMD-1为斥力或吸力后的位移和加速度峰值分别为0.869 mm和0.023 94 m/s2，0.718 mm和0.018 865 m/s2、1.0 mm和0.027 535 m/s2。

测得EMTMD-2为斥力或吸力的磁路设计，位移和加速度峰值分别为0.8 mm和0.022 15 m/s2、0.513 mm和0.013 75 m/s2。计算得到加速度和位移减振率如图12所示。

由图12可知，结构模型安装电涡流阻尼器，EMTMD-1为斥力或吸力，EMTMD-2为斥力或吸力后的位移和加速度的减振率分别为89.20%和89.80%，91.14%和92.00%、87.60%和88.30%，89.40%和90.60%、93.60%和94.10%。结构模型安装EMTMD-1为斥力，EMTMD-2为吸力或斥力的减振率分别高于电涡流TMD的1.94%和2.20%，4.40%和4.30%、0.20%和0.80% ，而安装EMTMD-1为吸力的减振率低于电涡流TMD的1.60%和1.00%。

(a)

尽管安装磁力阻尼系统，EMTMD阻尼比变化微弱，但是合适的磁路设计可提高减振率，从而说明电涡流-磁力混合阻尼减振效果优于电涡流阻尼。因此磁铁最佳磁路设计EMTMD-1应为斥力，EMTMD-2应为吸力。对于EMTMD-3的磁路设计需要结合EMTMD-1和EMTMD-2减振效果显著的方案来设计，即铜板后磁铁和相对的运动磁铁表面磁性相同，底板上磁铁和同一侧的运动磁铁表面磁性相反。确定EMTMD磁铁的最佳磁路设计后，需进一步确定磁铁尺寸。

4.2 磁铁尺寸对EMTMD减振控制的影响

为探究磁铁尺寸对EMTMD减振控制的影响，将分别在EMTMD上安装不同磁铁对结构模型进行减振控制。每种工况都以相同输入进行激励：即在信号发生器输出激励频率4 Hz，激励幅值10 VPP使激振器激励结构模型发生共振。将上述设计的不同工况下EMTMD-1、EMTMD-2、EMTMD-3分别对结构进行减振控制。每次测量得到阻尼器稳定工作后的位移和加速度峰值如图13所示。

由图13可知， EMTMD-1、EMTMD-2、EMTMD-3安装磁铁尺寸分别为20 mm×20 mm×5 mm、30 mm×20 mm×10 mm，20 mm×10 mm×5 mm、30 mm×20 mm×10 mm减振效果最好，由式(3)和式(4)以及表3数据计算出3种工况最大磁力分别为46.69 N，81.8 N，123.22 N。此时结构模型位移和加速度峰值分别为0.611 mm和0.015 3 m/s2，0.421 mm和0.012 315m/s2，0.331 mm和0.011 15 m/s2。据此计算得到不同磁铁尺寸下EMTMD的位移和加速度减振率分别如图14所示。

(a) 位移曲线

由图14可知，EMTMD-1、EMTMD-2、EMTMD-3控制效果最佳的工况对应的位移和加速度减振率分别为92.49%和93.56%，94.80%和94.80%，95.90%和95.30%，对应的电涡流阻尼系数和磁力阻尼系数之比分别为0.37、3.00、0.75。在铜板后安装磁铁和底板上安装磁铁制作的EMTMD，均能在电涡流TMD减振控制的基础上提高减振性能，但是在铜板后安装磁铁的磁路设计的EMTMD减振率小于底板上安装磁铁。其原因为铜板后安装磁铁会降低电涡流阻尼力，而底板上安装磁铁对电涡流阻尼力影响较小。

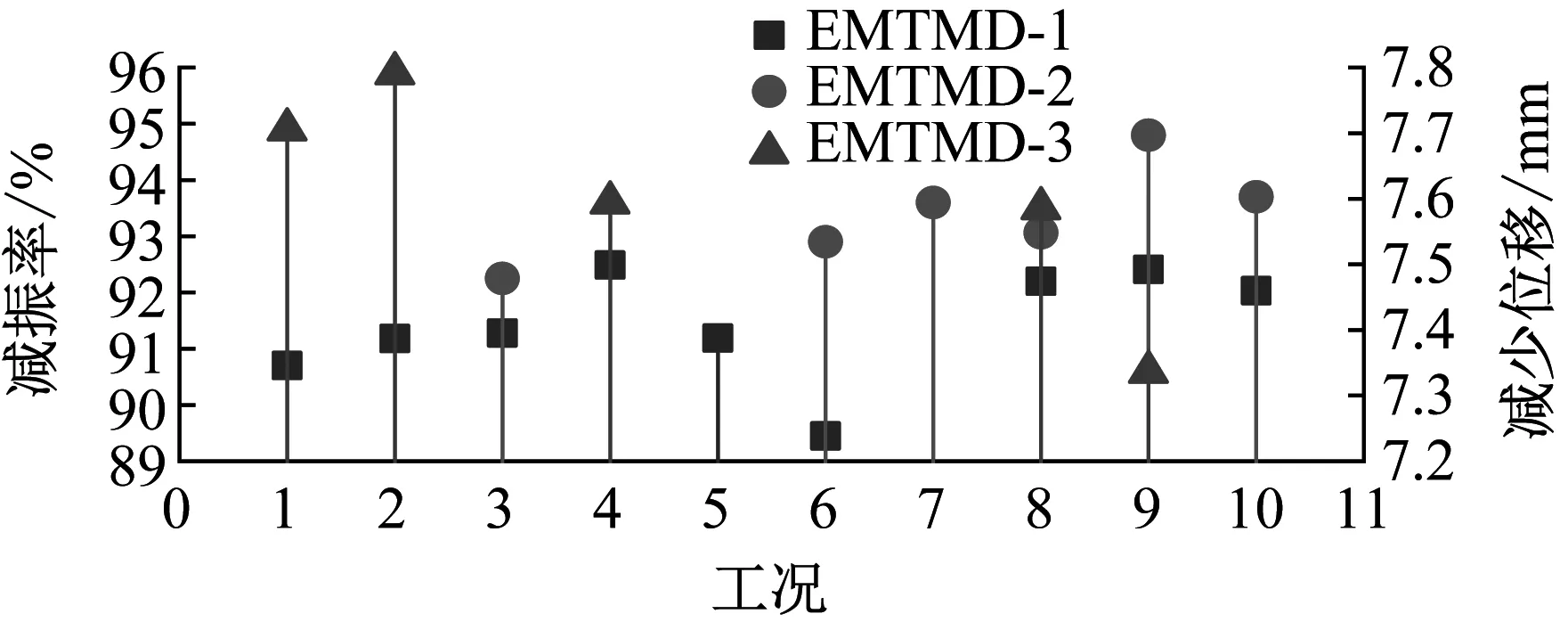
(a) 减振率-减少位移曲线

4.3 不同激励频率下EMTMD对结构模型的减振控制影响

为探究EMTMD对结构模型的减振控制效果受激励频率的影响，特将EMTMD放在结构的中间位置进行试验。本文分别选取2 Hz、3 Hz、4 Hz、5 Hz进行激励。当激振器激励致使结构模型发生振动，选取TMD稳定工作以后的加速度和位移峰值作图，如图15所示。

(a) 频域-位移曲线

由图15可知，结构模型安装电涡流阻尼器EMTMD-1、EMTMD-2、EMTMD-3后当激励频率为4 Hz时的位移和加速度最小，其数值分别为0.884 mm和0.023 94 m/s2，0.611 mm和0.017 6 m/s2，0.421 mm和0.017 6 m/s2，0.331 mm和0.017 6 m/s2。由此计算各个工况减振率如图16所示。

由图16可知，当激励频率为f/2、f时，结构会产生较大响应，减振率较大。当结构模型发生共振时，电涡流TMD，EMTMD-1、EMTMD-2、EMTMD-3的位移和加速度减振率分别可达89.6%和89.9%，92.5%和93.5%，94.8%和94.8%，95.9%和95.2%。同一激励频率，减振率EMTMD-3>EMTMD-2>EMTMD-1>电涡流TMD。说明EMTMD具有很好的减振耗能作用。从2 Hz到4 Hz，电涡流阻尼器位移的减振率变化9.1%，EMTMD-3位移的减振率变化6.2%。说明EMTMD-3对结构的控制效果比电涡流阻尼器的更加稳定。

4.4 不同激励幅值下EMTMD对结构模型的减振控制影响

为探究EMTMD在不同激励幅值下对结构模型的减振控制问题，特将EMTMD-3放在结构的中间位置进行试验。输入简谐荷载频率为结构自振频率1倍能更好的保证TMD的鲁棒性。为此让激振器激励频率为4 Hz，激励幅值分别为5 VPP、10 VPP、15 VPP，对结构模型进行激励。为了进行有效对比，首先将激振器摆放在结构模型跨中，对未安装减振装置、安装电涡流TMD、 EMTMD-3后的结构模型进行激励。每次选取TMD稳定工作以后的位移和加速度峰值如表4所示。

表4 不同激励频率下结构振动响应

由表4可知，同一激励幅值，EMTMD-3的位移和加速度最小。结构模型安装EMTMD-3后的位移和加速度是同工况下安装电涡流阻尼器的1/2。同时根据表4数据计算得到加速度和位移减振率，如图17所示。

由图17可知，随着激励幅值由5 VPP变化到15 VPP，电涡流阻尼器减振率变化4.4%，EMTMD-3减振率变化2.4%。由此可见激励越大EMTMD-3越稳定，当面对较大激励EMTMD-3有良好稳定的减振作用。并且每种工况下，EMTMD-3减振率均高于电涡流TMD，最高可达95.9%，比同工况下电涡流TMD减振率高6.8%。电涡流TMD控制效果能够达到EMTMD-3的92.9%，由此可知EMTMD比传统的电涡流TMD有更好的减振控制作用。