隧道爆破振动信号的混沌特征分析

2022-02-22谢全民贾永胜凌正东刘鼎盛

振动与冲击 2022年3期

谢全民，贾永胜，丁凯，张杰，凌正东，刘鼎盛

(1.江汉大学省部共建精细爆破国家重点实验室，武汉 430056； 2.江汉大学爆破工程湖北省重点实验室，武汉 430056；3.陆军研究院五所，江苏无锡 214025； 4.四川交博环境检测公司，成都 610031； 5.陆军工程大学军械士官学校，武汉 430075)

采用钻爆法开挖隧道时，经常会遇到既有隧道爆破安全问题。如何控制爆破开挖产生的爆破振动危害效应，确保既有隧道结构安全、邻近隧道爆破项目高效施工，是建设部门、施工单位、行政主管部门等多方共同面临的重大技术难题。其中在邻近爆破施工对既有隧道影响研究方面，国内不少专家学者开展了专项研究。钟冬望等[1-2]采用动力有限元程序，对邻近隧道掘进爆破作用下既有隧道的质点振动速度和应力分布情况进行了计算。蒋楠等[3]通过现场试验和数值模拟，分析爆破振动作用下既有隧道结构动力响应特性。刘冬等[4]基于原有隧道改扩建拱顶塌腔段扩建开挖，系统研究了多临空面条件下岩体爆破振动规律。叶培旭等[5]实时监测近距离交叉隧洞爆破施工对既有隧道的振动影响。杨明宇等[6]研究了邻近隧道爆破开挖对既有隧道影响及控制技术。

时间序列分析是探究复杂动力系统机理、建立系统模型的重要手段。爆破振动时域测试信号特征提取，对准确掌握既有隧道结构在邻近隧道爆破作用下的结构动力响应规律具有重要作用。近年来小波、提升小波、尔伯特-黄变换、分形、多重分形、支持向量机等数字信号分析技术在爆破振动实测信号分析中得到了广泛应用[7]。

非线性科学是主要研究非线性现象的共性，其中混沌和分形构成非线性科学的主体。近年来混沌时间序列研究也是信号分析领域中的热点[8]。受系统演化及外界干扰影响，爆破振动实测数据呈现非平稳、含噪声等特点。本文基于混沌理论，将邻近隧道爆破及上跨坑道爆破作用下既有隧道振动响应时间序列进行相空间重构，通过吸引子、Lyapunov指数、关联维数等核心参量计算，分析隧道爆破振动响应信号混沌特征，可为下一步开展邻近隧道爆破作用下既有隧道振动响应的动力学机制研究奠定重要的基础。

1 邻近隧道爆破作用下既有隧道振动响应试验

1.1 试验地点

某山岭隧道设计为双洞单线隧道，上行线全长23 468.5 m，下行线全长23 441 m。由于复杂地质构造、地下水变化等特殊地质灾害因素导致隧道灾害。上行线隧道需要整治段落共计4 490 m，下行线整治在上行线整治完成后进行。隧道灾害处置采取全环拆换处理，按照先加固后拆换的原则，对拆换段落围岩采用钻爆法进行扩挖，增大二次衬砌净空横断面及仰拱混凝土厚度。上行线钻爆作业面与既有运行铁路隧道相平行，隧洞间距仅30 m。本次邻近隧道爆破对既有隧道振动影响试验依托该隧道整治项目K298+180～K299+400施工段进行，如图1、图2所示。

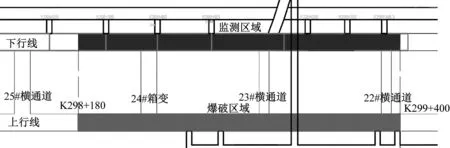
图1 爆区与保护区的位置关系示意图

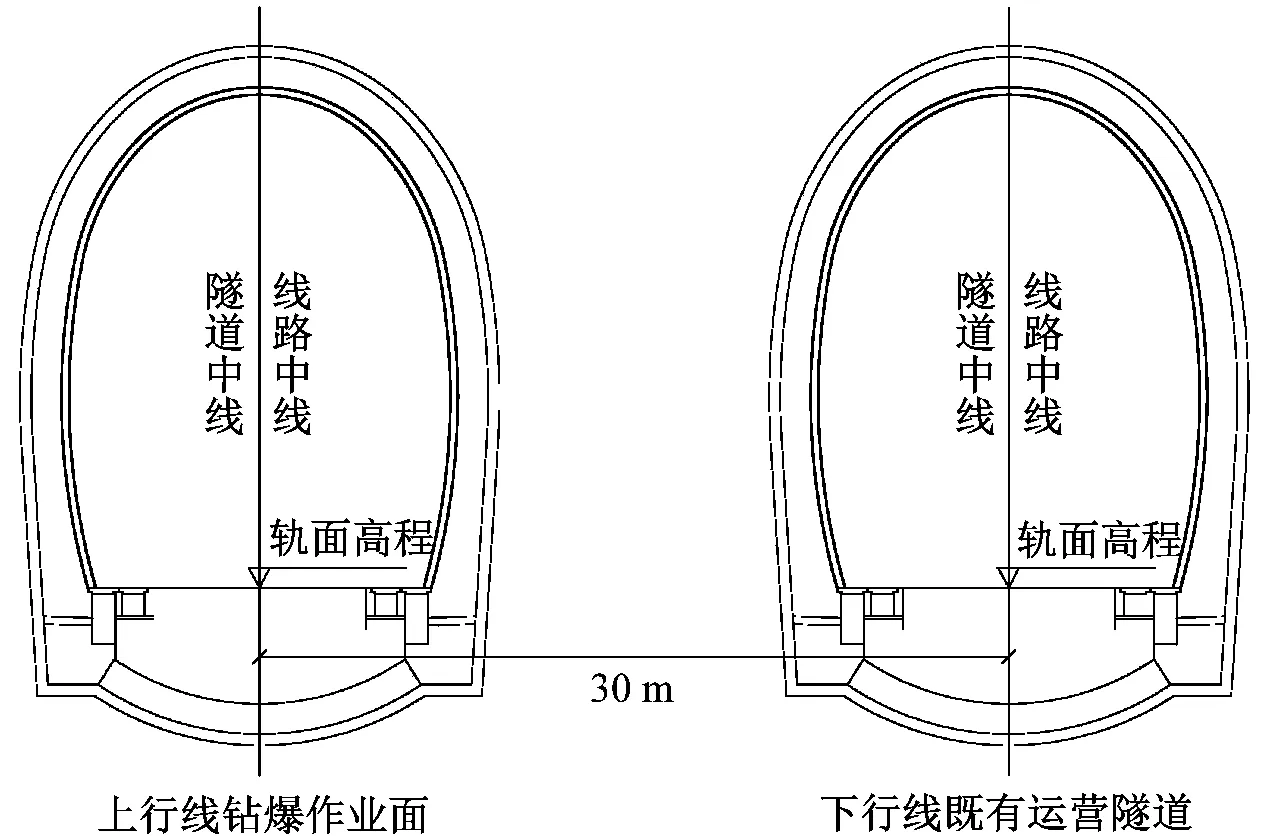
图2 爆区与保护区的位置关系剖面图

1.2 试验设备

试验采用L20-N爆破测振仪，属于远程无线网络爆破测振仪，可无人值守、远程监控的数字爆破测振设备。隧道爆破时，对既有隧道在邻近隧道爆破作用下的振动信号进行采集，并将结果通过网络传输至指定的数据中心，如图3所示。

图3 L20-N爆破测振仪

1.3 试验方案

(1) 传感器安装：传感器布设在邻近隧道内迎爆侧边墙墙脚位置。传感器通过膨胀螺栓固定，信号线沿墙脚牵引至控制箱，监测点胀螺栓采用M6×60安装，钻孔深度40 mm，清孔后按照JGJ 145—2013 《混凝土结构后锚固技术规程》要求进行安装，监测点布置，如图4所示。

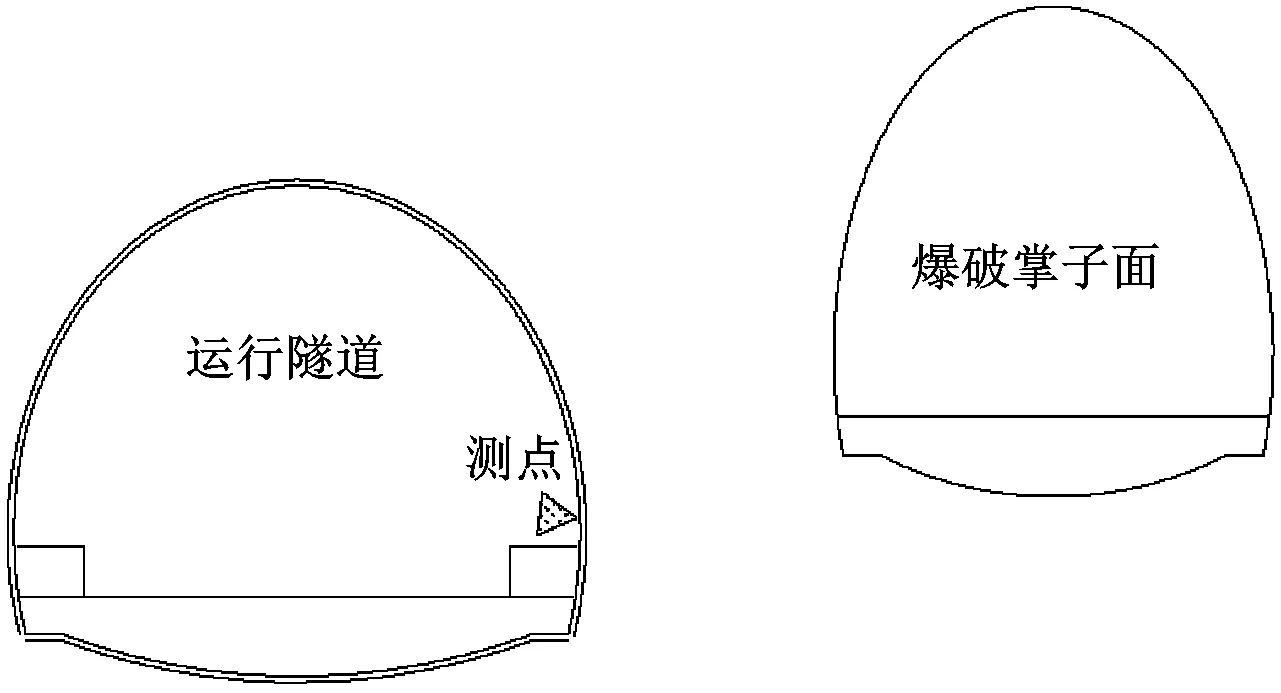
图4 爆破振动监测点平面布置示意图

(2) 测点间距：20 m，监测点平面布置，如图5所示。

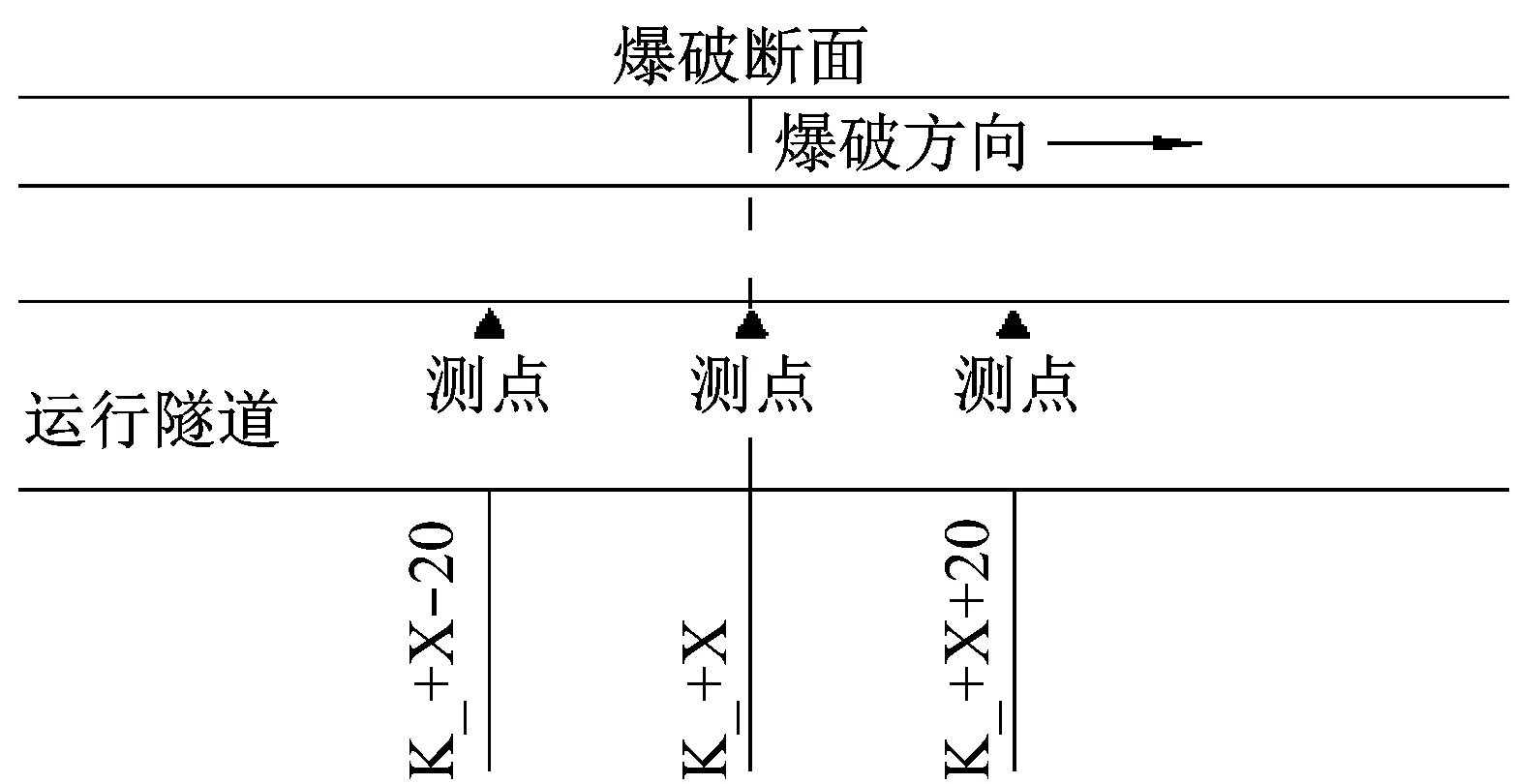
图5 爆破振动测点纵断面布置示意图

(3) 传感器数量：每个爆破作业面配置3台爆破测振仪，该组监测点随爆破掌子面里程而平移。

(4) 测试范围：K298+180～K299+400。

(5) 采样率：2 K。

2 隧道爆破振动信号的相空间重构

2.1 相空间重构

为研究邻近隧道爆破作用下既有隧道振动响应的动力学机制，分析隧道爆破振动响应时间序列的非线性特征，需将振动实测信号的一维单变量时间序列映射到多维空间，由矢量点重构成新的状态空间(相空间)。原爆破振动动力系统的规律将呈现为高维特征空间的一种轨迹，可通过提取其中某个分量的一批时间序列数据，从中得以恢复。

Takens[9]研究表明，设延迟坐标维数为m，若m>2d(d为动力系统的维数)，则可找到一个合适的嵌入维数m，在该嵌入维空间中恢复吸引子运动轨迹。

2.2 C-C法基本原理

设一维爆破振动时间序列{x1,x2,…,xN}，把它分成t个互不相交的子序列(t∈N)，则

(1)

(1) 根据Takens嵌入定理，定义关联积分函数[10]

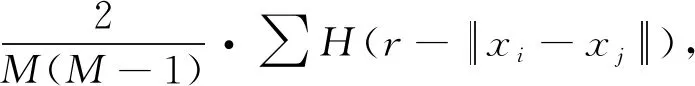
r>0

(2)

式中：H(r)为Heaviside阶跃函数

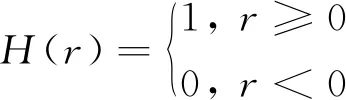
(3)

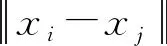
(2) 定义关联积分的统计量

s(m,N,r,t)=C(m,N,r,t)-Cm(1,N,r,t)

(4)

当N→∞时，则

(5)

(3) 定义差量ΔS(m,t)，表示S(m,r,t)关于r的变化。

ΔS(m,t)=max{S(m,tj,t)}-min{S(m,rj,t)}

(6)

(4) 对所有S(m,rj,t)求平均得

(7)

2.3 重构相空间的延迟时间

Brock等[11]通过多种渐近分布产生时间序列的相空间重构分析表明，当m∈[2,5],r∈[0.5δ,2δ]时(δ代表时间序列的均方差)，S(m,N,r,1)能够代表在数据长度范围N以内的连续相关性。为判断某时间序列是否具备混沌性质，N通常取100～500即可；对该时间序列进行相空间重构时，N建议取值3 000以上。

重构时取m=2, 3, 4, 5，r=0.5δ,δ, 1.5δ, 2δ，则

(8)

(9)

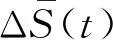
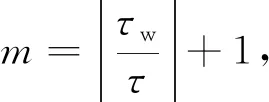
(10)

2.4 混沌吸引子的关联维

选取适当的r使得C(r)=rD，D为相空间中混沌吸引子的关联维数。

当不断提高嵌入维数m时，线性部分斜率不再随m的增大而发生改变，这时维数达到饱和，称m为饱和嵌入维数，相应斜率即是所要求的关联维数D。

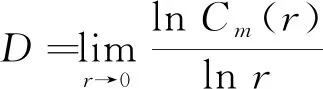
(11)

3 邻近隧道爆破作用下既有隧道振动信号的混沌特征分析

对上行线爆破开挖过程中，为不失一般性将其中K298+560、K298+940、K299+360 3个不同爆破掌子面上分别采用一个测点数据进行隧道爆破振动混沌特征分析。

所选取的3个爆破振动速度时程信号，如图6所示，均具有隧道爆破过程中微差爆破振动响应信号的典型特征。所选取的试验数据具有代表性。

3.1 典型爆破振动信号的延迟时间

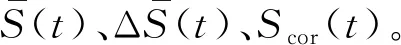
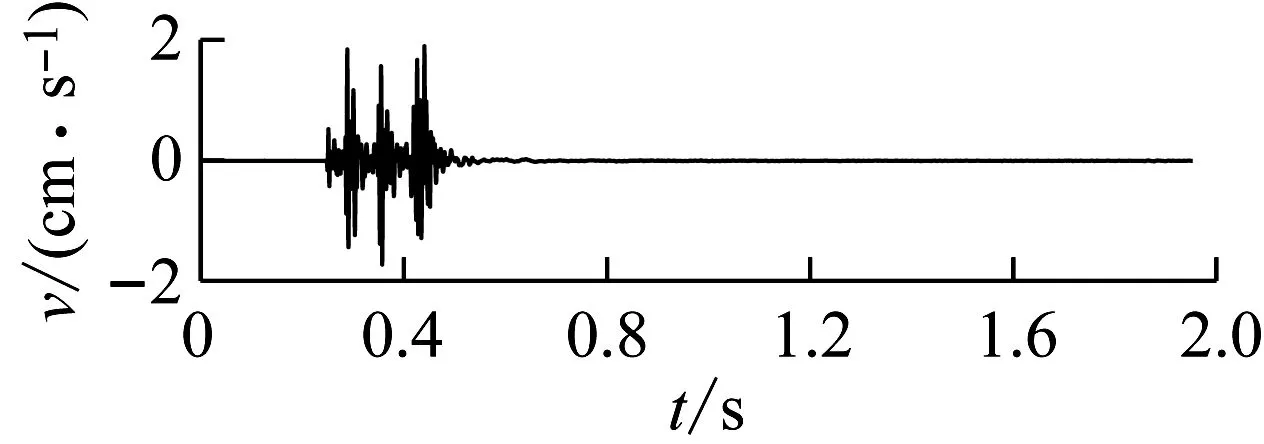
(a) 信号X：K298+560，垂向

分析图7(a)，delt-s曲线的第一个极小值点对应t=10，s-cor曲线的全局极小值点对应t=10，因此确定信号X的延迟时间τ为10，延迟时间窗τw为10，最小嵌入维数m为|10/10|+1=2。

分析图7(b)，delt-s曲线的第一个极小值点对应t=12，s-cor曲线的全局极小值点对应t=21，因此确定信号Y的延迟时间τ为12，延迟时间窗τw为21，最小嵌入维数m为|21/12|+1=2。

分析图7(c)，delt-s曲线的第一个极小值点对应t=13，s-cor曲线的全局极小值点对应t=17，因此确定信号Z的延迟时间τ为13，延迟时间窗τw为17，最小嵌入维数m为|17/13|+1=2。

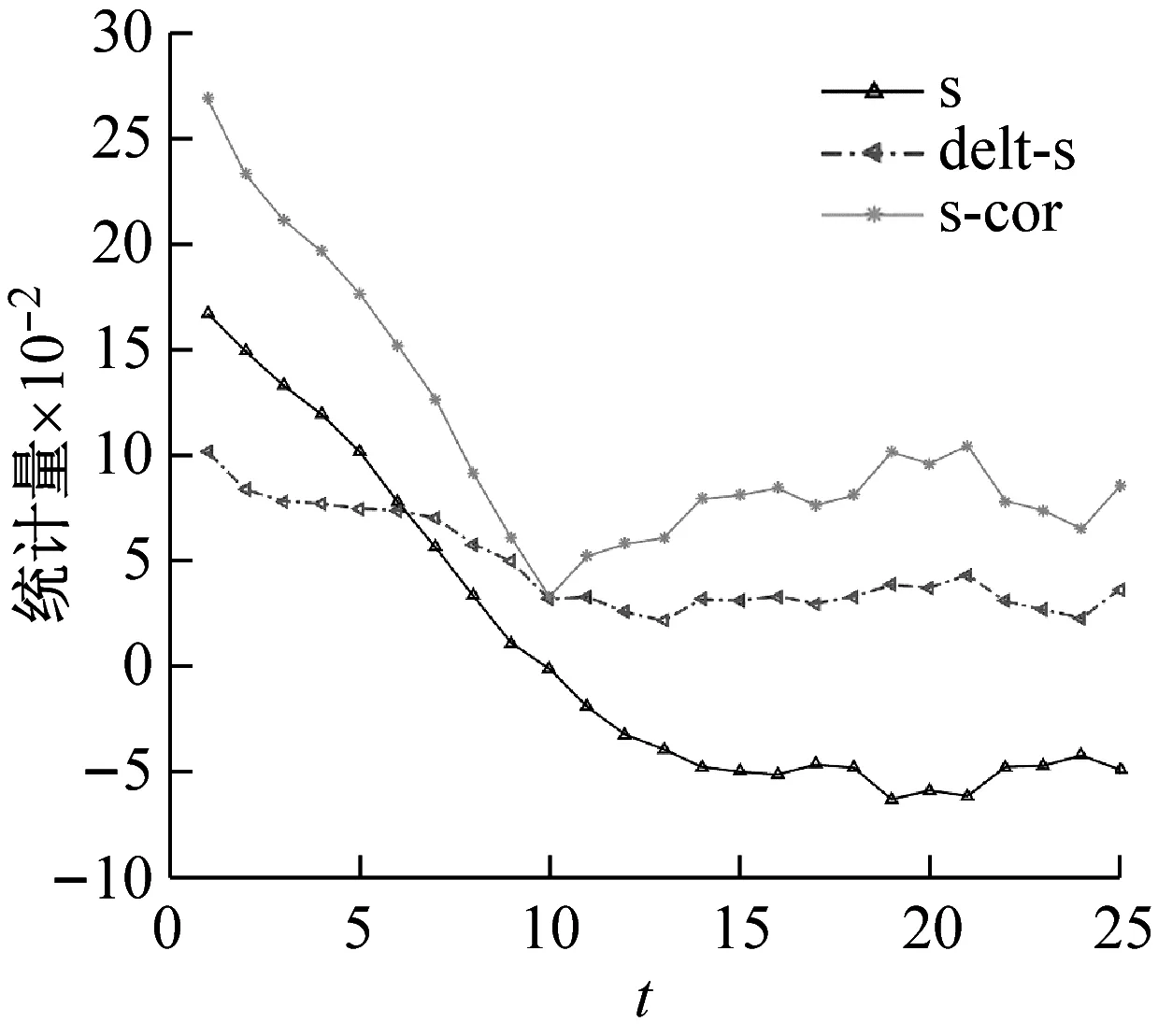
(a) K298+560/信号X

3.2 关联维数特征

对图6中Y信号使用采样点数N=4 000，嵌入维数m∈[2,16]，延迟时间τ=12进行相空间重构，得到该信号的累积能量时间序列lnC～lnr的双对数曲线，如图8(b)所示，可得m=10，D=1.45。

对图6中Z信号使用采样点数N=4 000，嵌入维数m∈[2,16]，延迟时间τ=13进行相空间重构，得到该信号的累积能量时间序列lnC～lnr的双对数曲线，如图8(c)所示，可得m=12，D=1.76。

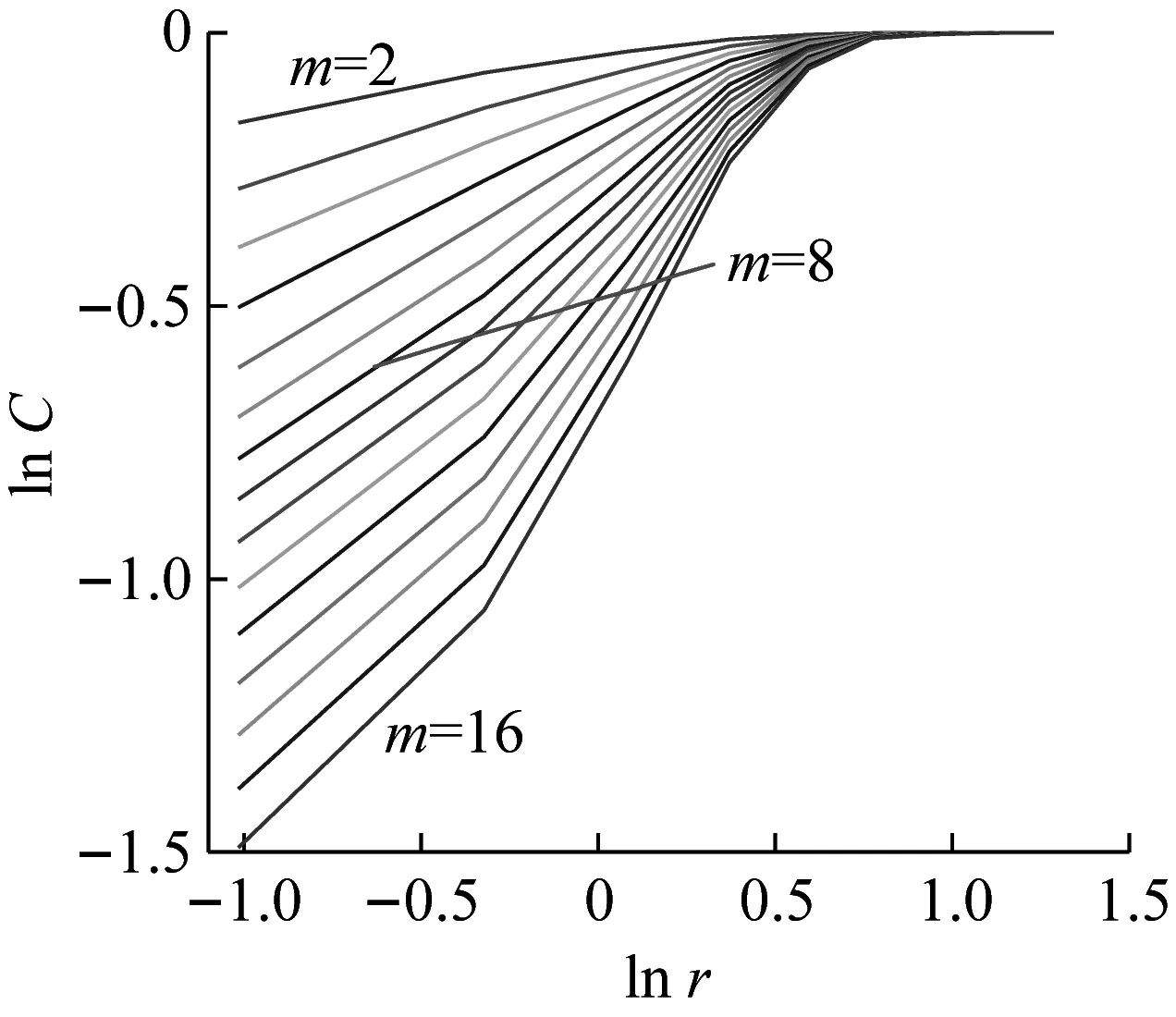
(a) 信号X

3.3 相轨迹图变化特征

判别信号混沌特征可采用吸引子轨迹法[13]。对图6中对应的3个隧道爆破振动时域信号进行相空间重构，绘制相空间轨迹图可直观清晰地体现出各个振动信号系统状态的演变过程，图9为计算得到相应信号的混沌吸引子演化过程。

分析图9可以发现，3个典型的隧道爆破振动信号的混沌吸引子形态均为具有无穷嵌套自相似结构的不相交环面组成，且都聚集在相空间的有限区域内，表明3个信号呈现混沌弥散状态。

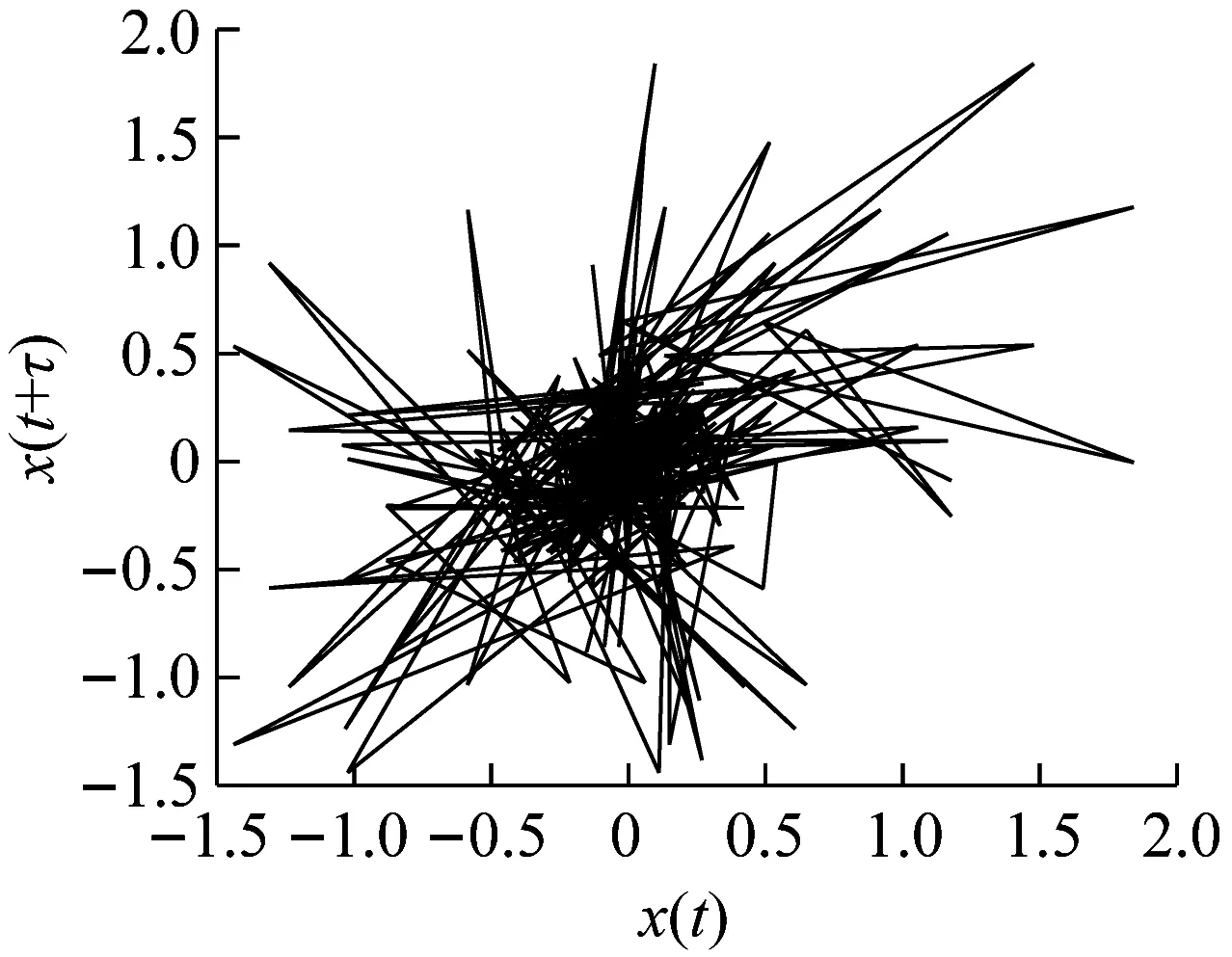
(a) X信号

3.4 Lyapunov 指数特征

混沌特征量是描述动力系统混沌特性的参数，对混沌现象研究有重要意义，主要包含Lyapunov指数、分数维数和熵。Lyapunov指数是三者中最直接描述系统混沌现象的参量。

对初始条件极为敏感是混沌运动的基本特征之一。两个距离很近的初值产生的轨道，随时间的变化按照指数方式分离，可以用Lyapunov指数来定量描述这一物理现象。

设由平均每次迭代产生的指数分离中的指数为λ，经过n次迭代后初始距离为ε的两点间距变为

εenλ(x0)=|Fn(x0+ε)-Fn(x0)|

(12)

令ε→0,n→∞，式(12)变为

没过一会儿，天黑尽了，孩子们叮叮咚咚地敲门：阿妈，让我们进来！我们饿了。有几个孩子哭了起来。甲洛洛很奇怪：你们怎么把孩子们关在外面？登子赶忙起身去开门：嚯嚯，原来天都黑了！

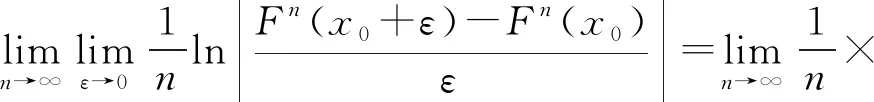
(13)

经过变形简化计算，可得

(14)

Wolf等[14]提出了可直接基于相空间内的轨线、平面及体积等演化途径来进行Lyapunov指数估计的算法，被称作Wolf法，在时间序列混沌研究领域得到了广泛的应用。因此采用Wolf方法分别计算图6中3个爆破振动信号的Lyapunov指数，结果如表1所示。

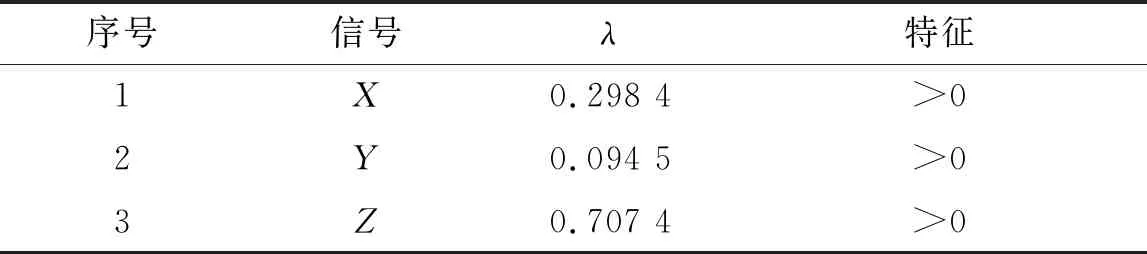
表1 Lyapunov指数计算结果

3.5 混沌特征分析

混沌常出现在确定性系统中，被认作一种看似无规则、类似随机的现象。混沌看不出明显周期性和对称性，并非简单的无序结构，实际是一种有序结构，内部包含丰富的层次，是非线性系统中一种新的存在形式[15]。

从邻近隧道爆破作用下既有隧道爆破振动信号重构吸引子图9可以看出，3个吸引子都是振荡曲线。可以看出，这种振荡是非周期的，且包含随机性，不管经历多长时间它们不会与之前某时刻的振荡发生完全重复，且这3个轨迹是有限的，被限制在有限的相空间中。因此，这3个吸引子属于奇怪吸引子。混沌运动就是具有奇怪吸引子的运动，从试验得到的一维时域信号相轨迹图变化特征可判定邻近隧道爆破作用下既有隧道振动响应具有混沌特征。

由一维时域信号的Lyapunov指数定义及求解方法可看出，当λ<0时，轨道对初始条件不敏感，相空间会渐渐收缩，相邻点最终聚集成一个点，属于稳定的不动点或周期运动系统；当λ=0时，初始误差保持不变，系统处于临界状态；当λ>0时，表示相邻点会逐渐分离，相应的是局部轨道不稳定状态。判定某动力系统是否存在混沌行为，可由λ是否大于0来作为判据[16]。经过相空间重构，从邻近隧道爆破作用下既有隧道爆破振动试验数据的Lyapunov指数计算结果表1可以看出隧道爆破振动信号的Lyapunov指数均大于0，进一步证明邻近隧道爆破作用下既有隧道振动响应信号具有混沌特征。

4 上跨坑道爆破作用下既有隧道振动混沌分析

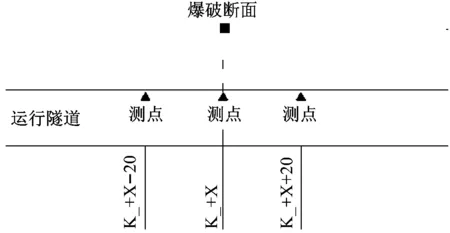
在隧道整治项目K298+180～K299+400施工段中，4#工区辅助上跨坑道是垂直于既有运营铁路隧道的直线通道。辅助坑道与4#斜井交界处距离下行线既有铁路隧道水平最远距离106.7 m，坑道底部距离下行线既有铁路隧道顶部11 m。辅助坑道采用钻爆法开挖，爆破区域里程为DK312+616，对应运营隧道保护区域里程为K299+000，爆破区域与既有铁路隧道保护区域的位置关系，如图10、图11所示。传感器布置，如图12所示。采样率设置为2 K。

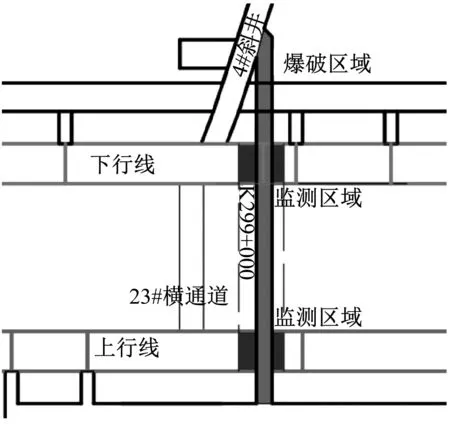
图10 上跨坑道与既有铁路位置关系示意图

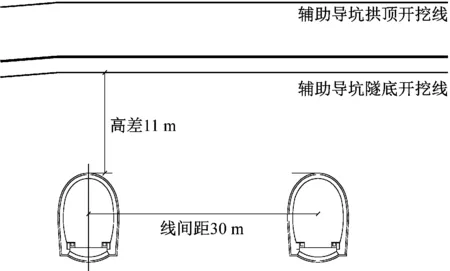
图11 上跨坑道与既有铁路位置关系剖面图

(a)

对上跨坑道掘进爆破过程中产生的爆破地震波作用下下行线既有隧道结构的振动响应采用L20-N爆破测振仪进行测试，其中K298+980、K299+000、K299+020 3个测点处分别采集到3个炮次的爆破振动信号。X方向为水平径向，Y方向为水平切向，Z方向为垂直向。

为系统分析上跨坑道爆破作用下既有隧道动力系统的混沌特性，对试验采集的9组时域信号(X、Y、Z向)分别进行相空间重构，采用C-C法计算得到27个信号延迟时间、嵌入维数m，在此基础上基于Wolf法计算混沌重要特征量Lyapunov指数如表2所示。

分析表2可知，9组27个信号进行相空间重构后所得到的Lyapunov指数均大于0，表明上跨坑道钻爆法开挖地震波作用下其正下方11 m距离的下行线既有铁路隧道的振动响应也具有混沌特征。

对K0+00、K0+15、K0+25 3个位置爆破作用下，K298+980、K299+000(垂直)、K299+020 3个测点的Lyapunov指数计算结果表2分别进行分析可看出：

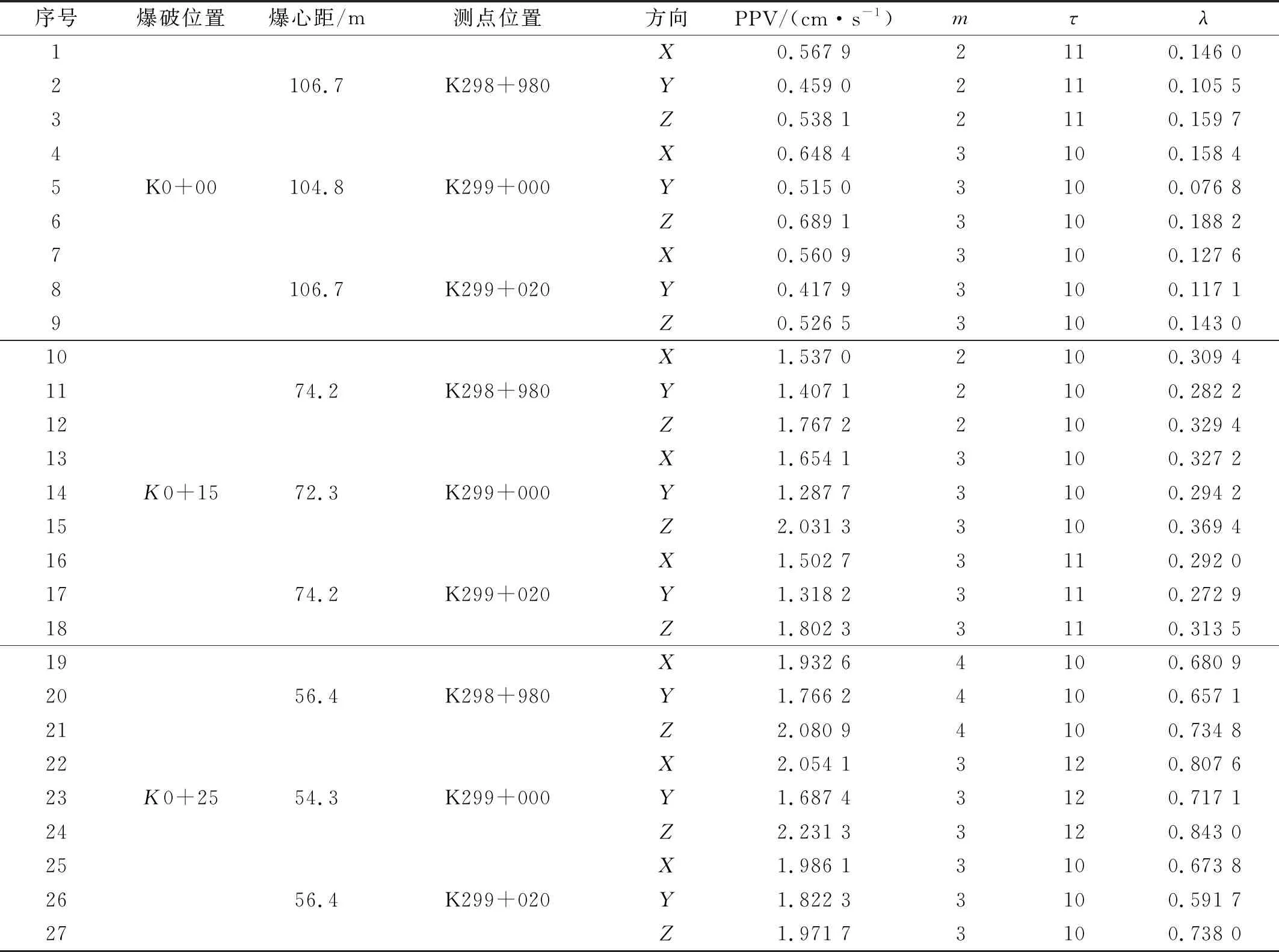
表2 上跨坑道爆破振动混沌特征值计算

(1) 每次爆破作用下，K298+980、K299+020两个测点爆心距相等，两个测点的X、Y、Z向振动信号的λ值也几乎相等；K299+000测点爆心距小于左右两个测点，λ值大于左右两个测点。

(2) K0+25位置爆破作用下的9个信号λ值大于K0+15、K0+00位置爆破作用下的18个信号λ值，K0+15位置爆破作用下的9个信号λ值大于K0+00位置爆破作用下的9个信号λ值，表明随着钻爆作业面与既有隧道爆心距减小，λ值变大，隧道爆破振动响应的混沌特征增强。

(3) 爆破作业面上岩石力学性质、掏槽方式、掏槽孔、辅助孔、周边孔钻孔参数、炸药种类、炸药单耗、起爆方式、循环进尺等爆源条件作为上跨坑道掘进爆破的重要初始条件，直接影响着钻爆法开挖上跨坑道的质量和效率，也是与之垂直相交的既有下行线铁路隧道爆破振动混沌动力系统的主要初始条件和重要影响因素。混沌系统的本质特点是对初始条件极为敏感，λ值变大则动力系统初始条件敏感性增强。因此随着爆心距的减小，上跨坑道爆源参数对既有隧道爆破振动影响加大。为确保爆破安全，随着爆心距减小应更加强钻爆参数的合理优化和爆破振动实时监测，确保既有隧道爆破振动响应控制在GB 6422—2014 《爆破安全规程》规定的安全阈值范围之内。