基于申威异构众核处理器架构的模态并行算法
2022-02-22喻高远马志强李俊杰金先龙
喻高远, 马志强,3, 李俊杰, 金先龙
(1.上海交通大学 机械系统与振动国家重点实验室,上海 200240; 2.上海交通大学 机械与动力工程学院,上海 200240;3.中国航发商用航空发动机有限责任公司,上海 200240)
随着交通运输业、能源勘探与开发业和航空航天业等的发展,对于大型、特大型装备的需求越来越多,如:高速动车组、3 000 m超深钻机、大飞机、跨江隧道、跨海大桥等。这些特殊装备系统的研制往往涉及大规模复杂动力学系统的计算,而模态分析则是其最耗费时间的计算环节,也是其余计算环节的基础,需借助大规模有限元模型进行高性能计算,故而对传统串行有限元计算方法和工具形成了挑战[1-2]。传统串行计算是以牺牲大型、特大型装备局部关键细节进行简化建模来保证计算效率,因而造成局部关键细节预测能力和大量密集模态的丢失,计算精度较低,无法满足其系统级高精度高效率数值分析的需求。随着并行计算机的快速发展,利用并行计算机研究和开发相应的并行算法则为大型、特大型装备系统模态的求解提供了切实可行的途径,正逐步成为各国学者的研究热点。
在硬件方面,异构众核分布式存储并行计算机具备计算能力强、性能功耗比高等优点,已成为当前超级计算机的重要发展方向,典型的异构众核处理器包括Intel的MIC、Nvidia和AMD的GPU、Godson-T以及申威众核处理器等[3]。近年来,国内外诸多学者在异构众核分布式存储并行计算机的基础上求解各类大规模、超大规模有限元系统,来获取系统的特性,取得了很好的效果。Koric等[4]利用并行SuperLU和PCG(preconditional conjugate gradient)算法基于GPU众核架构完成了某增压空气冷却器的瞬态动力学特性分析,其求解自由度超过千万。Martínez-Frutos等[5]采用CG(conjugate gradient)算法基于GPU众核架构完成了某L型悬臂梁的静态特性分析。杨梅芳等[6]使用直接数值模拟基于MIC众核架构完成了某发动机燃烧模拟分析。然而,国内外学者关于模态并行计算的相关研究较少,且多是以多核并行计算机和基于GPU众核架构的并行计算机为主。Heng等[7]基于多核并行计算机完成了模态叠加法并行算法设计,并将其应用于某悬臂梁的模态并行求解。朱彬等基于GPU众核架构设计了模态并行子空间迭代法,基于此完成了某风扇结构模态分分析。目前国内外基于申威众核处理器架构的模态并行求解算法研究相对较少,而基于申威众核处理器架构的并行计算机“神威太湖之光”在峰值性能、持续性能、性能功耗比3项关键指标均居于世界第一[8]。因此,利用基于申威众核处理器架构的并行计算机进行模态并行计算研究对于提高大型、超大型装备系统模态的计算规模、计算精度和计算效率具有重要意义。考虑到“神威太湖之光”并行计算机核组内通信时间远小于核组间通信,且其访存能力较弱,故利用“神威太湖之光”并行计算机提高并行效率的关键在于处理好大规模数据的存储以及各计算核心间的通信和协作问题。模态分析的数学实质可以归结为大型稀疏矩阵的广义特征值问题,该类问题的求解大多基于子空间类投影技术,主要包括Davidson类子空间方法和Krylov类子空间方法等。Davidson类子空间方法主要用于求解对角占优的对称矩阵特征值问题,其问题适应性不如Krylov类子空间方法。Krylov类子空间方法可以追溯到20世纪50年代提出的Lanczos算法和Arnoldi算法[9]。后来国内外诸多学者在Lanczos算法和Arnoldi算法的基础上进行了一系列重启动改进,比较著名的是:Sorensen等[10]提出的Arnoldi/Lanczos算法、Stewart等[11]提出的Krylov-Schur算法、Jia等[12-15]提出的加速子空间迭代法等。3种算法在数学上具有等价性,是目前Krylov类自子空间算法中的主流算法。与前两种算法相比,加速子空间迭代法更容易收敛,且代码实现难度较低,故本文采用加速子空间迭代法进行模态并行算法设计。
综上所述,本文基于国产申威异构众核分布式存储并行计算机和加速子空间迭代法分析了各计算步骤的计算量,根据计算结果构建了大规模模态分析并行计算体系,并将其应用于某超深钻井制动系统主体机构及某跨江隧道模态并行计算,实现了上千万自由度的模态并行求解。同时,该方法不仅通过分层策略实现了计算过程和数据通信的分层,有效提高了通信效率;而且通过计算数据的分布式存储,显著改善了数据访存效率。
1 大规模特征值问题求解算法
模态分析的数学的描述为
Kφ=λMφ
(1)
式中:K为模态系统整体刚度矩阵;M为模态系统整体质量矩阵;λ为模态系统广义特征值;φ为对应振型向量。K和M可以对工程结构进行有限元离散和积分得到,均为大型稀疏、对称(半)正定矩阵。模态分析的本质即求解式(1)的多个低阶特征对。采用子空间迭代法求解式(1)时,由于Krylov类算法大多数收敛于最大特征值,需采用Shift-Invert变换进行谱变换,其变换形式为
(2)
式中:σ为移位值;(K-σM)-1可通过变换求解线性系统的解获得
(K-σM)x=M
(3)
式(2)可改写为
Asν=μsν
(4)
式中:As=(K-σM)-1;μs=1/(λ-σ)。采用加速子空间迭代法求解式(1)的前m个特征值即求解式(4)的前m个特征值时,考虑到As的存储数据量为自由度规模n×n,为了最大限度降低中间变量As储存的内存占用空间,变量V(V可以取算法过程变量Q或者Y)与As做矩阵运算后的结果可通过求解式(5)所示的线性系统获得,其算法具体步骤如下所示。
(K-σM)(xV)=(MV)
(5)
步骤1输入矩阵K、M,求解特征值个数m,迭代初始向量Q,外层迭代控制误差ε,最大循环次数Maxcycle。
步骤2输出m个外部特征值λj和w。
(1) 初始化
随机生成初始向量Q,j=0,Y=[·],AA=[·],BB=[·],VV=[·],EE=[·],BBB=[·],LL=[·]。
(2) 进入求解m个特征值的循环
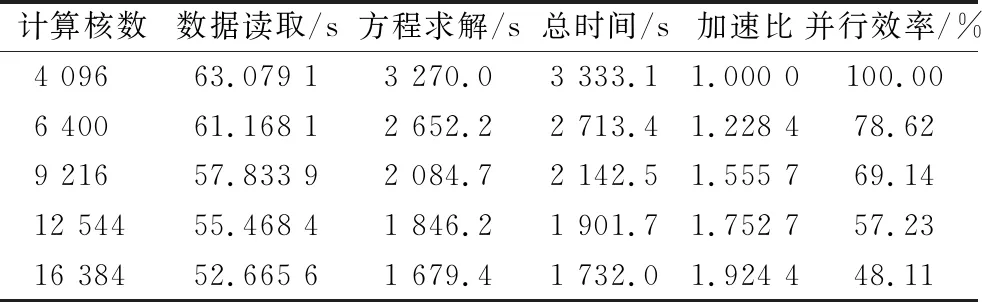
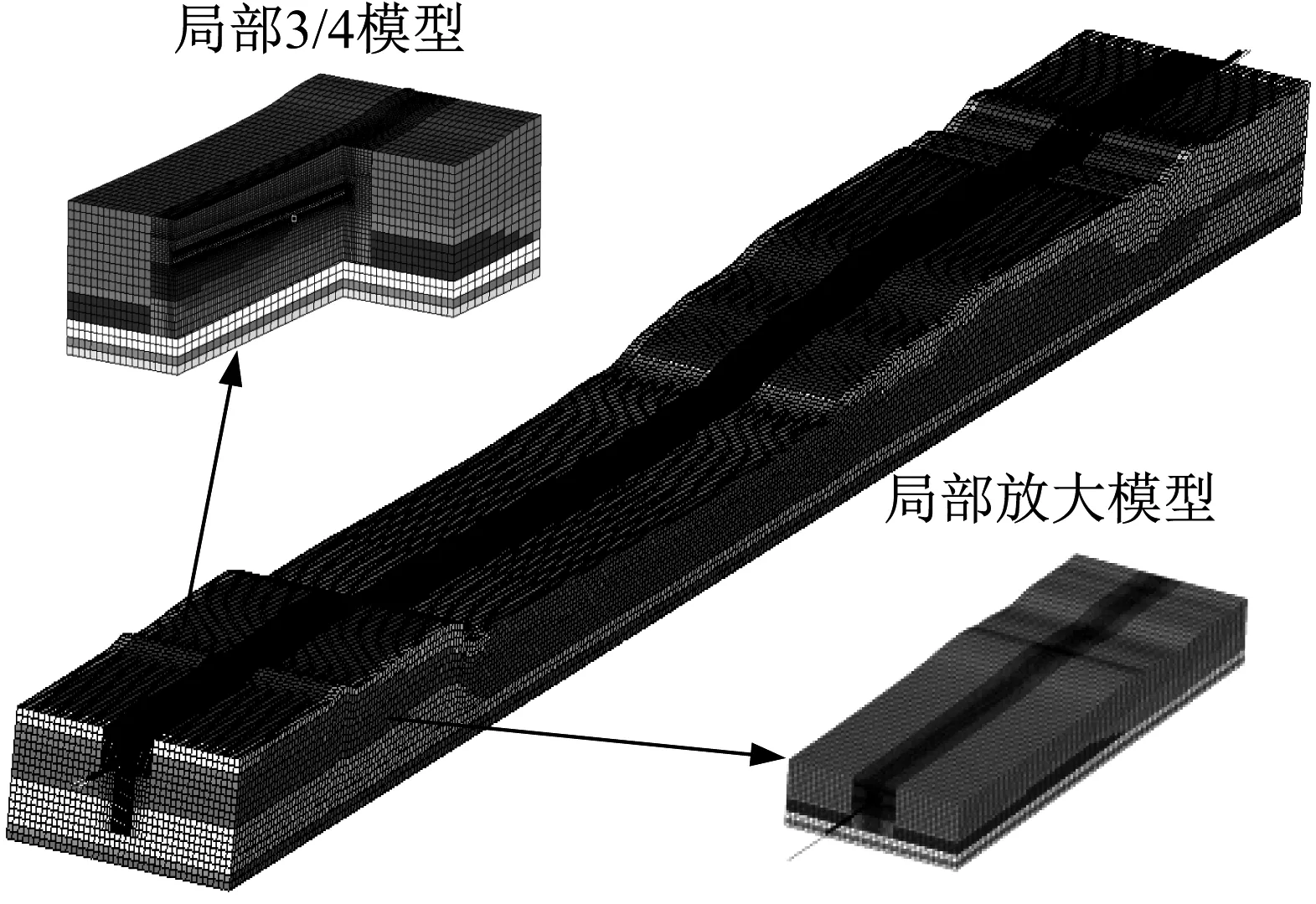
whilej ①计算:求解方程(K-σM)×(As×Q)=(M×Q)并将结果存储于Y中; ②计算:求解方程(K-σM)×(As×Y)=(M×Y)并将结果存储于Q中; ③计算:AA=Y′×Q; ④计算:BB=Y′×(E×Y); ⑤QZ法求解子空间上广义特征值问题:AA×ν=λj×BB×ν,式中,λj为第j次迭代求得的广义特征值; ⑥检查λj是否满足精度要求,若|(λj-λj-1)/λj|≤ε,则转到步骤4;如果不满足精度要求则作 BBB=((VV′×BB×VV)′+(VV′×BB×VV))/2 VV为ν构成的向量空间; ⑦对BBB做Cholesky分解并将产生上三角阵LL; ⑧计算:VV=VV/LL′; ⑨计算:Q=Y×VV; ⑩令j=j+1并返回步骤①; end while (3)检查 j 若满足,则转到步骤(4);如果不满足则输出计算有误; (4)计算 w=sqrt(λj)/(2π)并输出λj和w。 采用第1章算法,进行某超深钻进盘鼓式制动器转子盘模态分析,其有限元网格模型如图1所示,弹性模量为210 GPa,密度为7 800 kg/m3,泊松比为0.3。采用不同的自由度规模,固定约束其内表面8个螺栓孔位置,计算结构的前20阶固有频率,并与经典模态求解算法-Lanczos算法[16-17]的求解结果进行对比,各测试规模如表1所示,各自由度规模下20阶固有频率的最大相对误差按照式(6)计算后如图2所示。 图1 盘鼓式制动器转子盘有限元网格模型 (6) 由图2可知,各自由度规模下各阶固有频率的误差均不超过0.11%,表明:基于加速子空间迭代法的模态分析可以保证计算精度,故可用于模态并行算法设计。 图2 不同自由度规模下20阶固有频率的最大相对误差 不同测试规模下各步骤的时间比例如图3所示,由图3可知,随着自由度规模的增加,数据读取和特征值计算的时间比例逐步下降,初始化及方程求解的时间逐步增加,故而大规模模态并行算法设计的关键在于方程求解步骤的并行化,而特征值值计算可采用单节点计算,以减少通信耗时。 图3 转子盘不同测试规模下各步骤的时间比例 采用用申威众核处理器进行模态并行加速子空间迭代法设计,其架构如图4所示。 图4 申威众核处理器架构 每个申威众核处理器,共计4核组,各核组可共享32 GB内存。每个核组包括1个主核(运算控制核心)和64个从核(核心阵列)。核组间通信采用双向14 Gbits/s通信网络带宽,主核与从核间通信采用DMA(direct memory access)方式批量访问主存。从核局部存储空间大小为64 kB,指令存储空间为16 kB。 基于申威众核处理器及接口等功能形成的模态分析求解体系,如图5所示。 图5 模态分析并行计算体系 整个模态分析并行计算体系分为:多文件流数据读取、变量初始化及并行求解方程、并行求解模态固有频率3个部分。具体介绍如下: (1) 多文件流数据读取。各核组同步读取对应的刚度矩阵和质量矩阵数据文件,核组间无数据通信交流。刚度矩阵和质量矩阵是由组集系统模型的各部分结构化网格数据后并行求解获得[18]。 (2) 并行求解式(5)。考虑到大规模模态并行求解时需要求解式(5)两次,为了节约方程的求解时间,通过在申威众核处理器上集成并行LU算法来实现线性方程组的求解,在求解过程中组装的系统的单元刚度矩阵K仅需要进行一次LU分解,因而可以节约式(5)的总体求解时间。并行LU算法的实现过程如图6所示,主要包括矩阵并行Cholesky算法和三角线性方程组并行求解算法,其核心运算步骤为矩阵向量运算和数据通信。 图6 并行LU求解算法 数据通信包括核组间通信以及核组内通信,核组间通信采用MPI库实现,核组内通信采用Athread库实现。矩阵向量运算主要包含加减乘除,现以向量乘法a=b·c为例(a、b、c为任意矩阵向量运算过程中的存储数组),其实现过程如图7所示。各核组上64个从核同步从核组内存空间中循环读取对应数据,该部分数据段内存需小于64 kB进行计算后返回计算结果于指定位置,通信仅存在于各核组主核于从核之间。 图7 基于异构众核加速的矩阵向量乘法 (3) 并行加速子空间算法求解模态固有频率。按照算法操作属性主要包括:矩阵向量运算、QZ法并行求解广义特征值问题以及并行Cholesky分解等。进行矩阵向量运算的步骤主要为①~④、⑥、⑧,且QZ法并行求解广义特征值问题及Cholesky分解中均存在矩阵向量运算,其实现过程同图7所示。考虑到计算规模对于加速子空间各步骤时间占比的影响,步骤①~步骤④中的矩阵向量运算需各核组同步并行计算,存在核组间通信和核组内通信,QZ法并行求解广义特征值问题及Cholesky分解中的矩阵向量计算只在指定核组内进行运算,仅存在核组内通信。QZ法并行求解广义特征值问题的算法及并行Cholesky分解算法的实现如图8所示。 图8 QZ及Cholesky分解算法的并行化实现 基于搭建的模态并行求解体系完成某超深钻进盘鼓式制动器转子盘及某跨江隧道模态分析,求解模态阶数为前10阶。 对于该超深钻进盘鼓式制动器转子盘有限元模型,整体结构测试规模如表2所示。 表2 超深钻进盘鼓式制动器转子盘测试规模 为揭示复杂装备大规模模态计算的必要性及求解精度,对方案6~方案8的模态频率结果进行了比较分析,表3给出了3种规模下模态频率的对比情况。 由表3可知,同类型装置的各阶模态频率随着计算规模的增加,频率会逐渐下降,这是由于工程结构的有限元分析存在刚度矩阵的“硬化效应”,导致较小自由度规模计算时得到的模态频率偏高。对比方案6~方案8与方案1~方案5的模态频率,最大变化率4.39%,而方案6~方案8的模态频率变化率相对低的多,这说明对于类似于盘鼓式制动器转子盘这样的结构,需要提高相应的计算规模以提高其计算精度。 表3 转子盘不同测试规模下的结果变化 为了校验并行计算结果的正确性,图9给出了3种规模下模态频率与经典Lanczos算法对应的相对误差,由图9可知,3种规模下模态频率的计算结果与经典Lancozos算法的相对误差均小于0.687%,各阶振型保持一致,这就有效验证了本文并行计算结果的正确性。 图9 不同自由度规模下模态频率的相对误差 通过启动相应数目的节点机测试本文分层并行计算方法的性能,各规模下的计算结果如表4~表6所示。 由表4~表6可知,本文基于申威众核处理器架构提出的有限元模态分层通信并行计算方法能够获得较高的加速比和并行效率。这是由于分层通信策略实现了计算过程和数据通信的分层,各核组的主核仅负责数据的读取和全局通信,而各从核负责计算且仅与对应主核之间存在局部通信,因而可获得良好的加速比和加速效率。同时,为了进一步降低全局通信的次数和时间,考虑到组集形成的单元整体质量矩阵M需进行反复调用计算,将质量矩阵数据直接存储于各个核组存储空间中,可使得实际M参与的计算过程中,仅需要中间少量数据通信,而组集形成的刚度矩阵K需要进行LU分解,将其分布式存储于各个核组上,尽管这一过程会使得数据读取的并行可扩展性较差,然而对于大规模模态并行求解,数据读取占总时间的比例相对较低,其并行求解的关键在于如何降低全局的通信量,故可提高整体的加速比和并行效率。 表4 方案6并行计算结果 表5 方案7并行计算结果 表6 方案8并行计算结果 在表4~表6中,当计算核数由4 096增加到16 384的过程中,系统的总体并行效率发生了显著下降,这是由于模态计算过程中随着计算分区的增加,采用并行LU求解式(5)的过程中占用的内存和并行通讯也随之增加,导致系统的整体并行效率下降较大。 在实际的工程应用中,有时复杂工程结构会包含多种单元类型,为测试多单元混合建模千万自由度规模下复杂工程系统的并行效率,以图10所示的某跨江隧道模型为例进行分析,该模型具有2 896 781实体单元,186 121梁单元,21 685质量单元,自由度规模13 167 203,刚度矩阵非零元个数1 012 581 369,平均带宽412,求解其前20阶固有模态频率。 图10 某跨江隧道主体有限元模型 各计算核数下的测试结果如表7所示。由表7可知,对于包含多种类型单元千万自由度规模下的跨江隧道系统模态并行求解,本文所提出的模态并行计算方法仍然具有良好的加速比和并行效率。然而计算核数从12 544核提升至16 384核时,总体计算时间仅下降了715.2 s,下降幅度较小,这是由于LU分解和下(上)三角部分的并行求解不仅需要申请大量的内存,还需要大量的通信和计算。随着子区域的增加,尽管单个区域的计算时间有所降低,然而求解过程中通信开销会越来越大,致使系统总体计算时间降低较少,并行效率较低。与制动装备转子结构相比,该跨江隧道系统模型包含了多种类型的单元,可充分构建复杂工程系统的多单元混合模型,且仍然具备良好的并行效率和加速比,因而更加符合复杂工程系统的实际需求。 表7 某跨江隧道并行计算结果 (1) 为解决采用国产申威异构众核处理求解重大装备系统级模态并行求解问题,通过对模态加速子空间迭代法进行研究和集成开发,构建了一套大规模并行求解体系,该体系在模态加速子空间迭代法的基础上,利用分层通信策略不仅实现了计算过程和数据通信的分层,有效改善了通信效率,而且实现了计算过程中数据的分布式存储,显著改善了数据访存效率。 (2) 通过典型数值算例表明:对于完全实体单元建模和多单元混合建模下的系统级模型,该方法均能够获得良好的加速比和并行效率。并且具备上千万自由度规模的并行计算能力,基本可以满足重大装备和复杂工程系统利用国产处理器进行模态分析的需求。本文的研究结果对于重大装备和复杂工程系统的研制和使用均具有较强的指导意义和参考价值。2 模态加速子空间迭代法分析

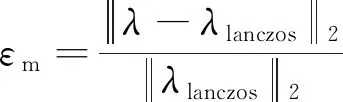

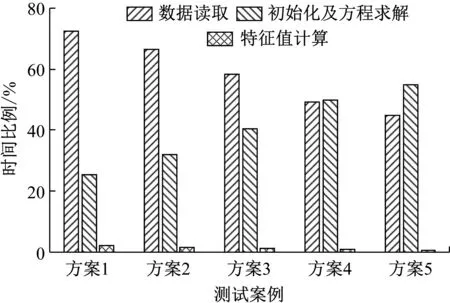
3 并行计算实现
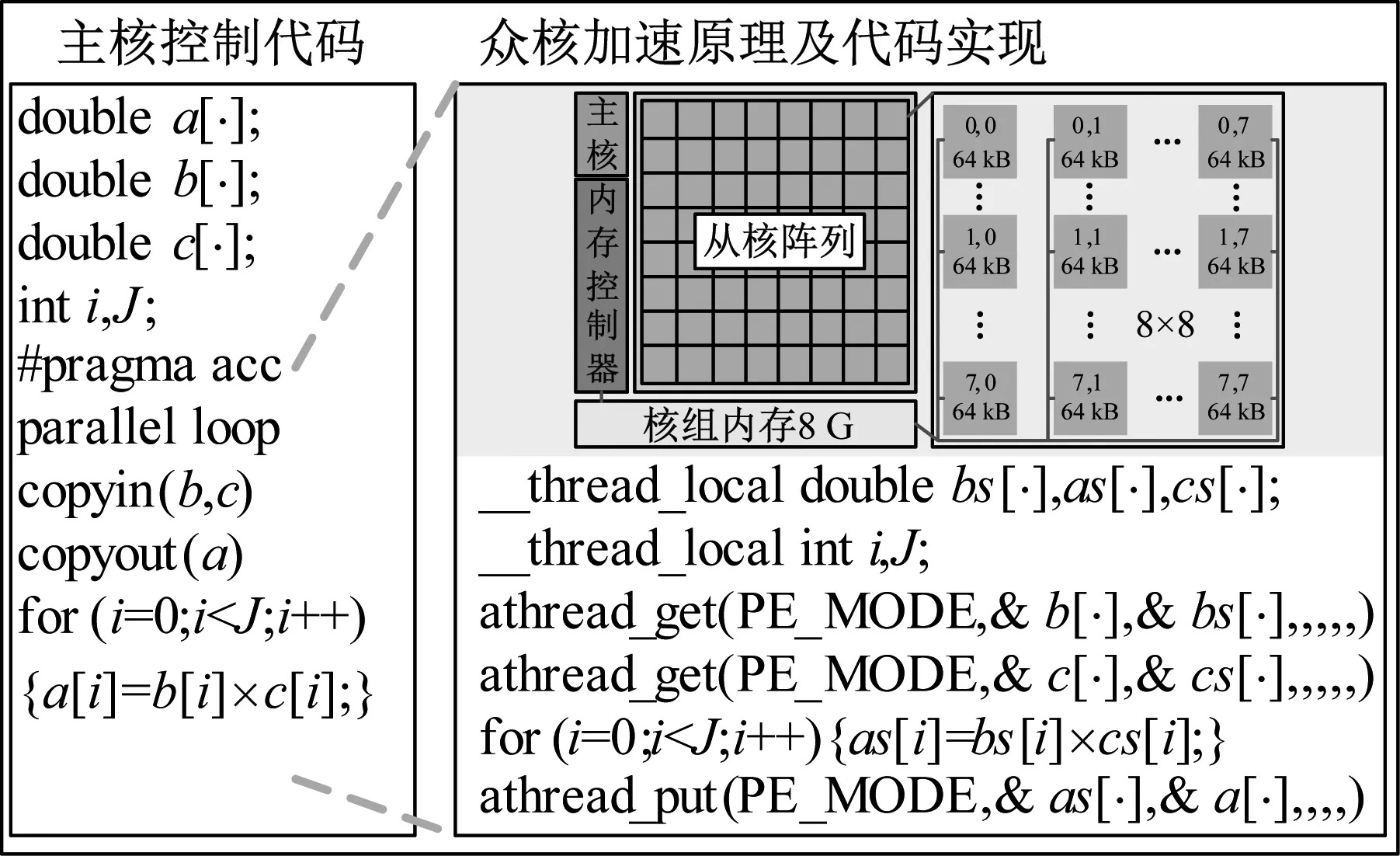
3.1 处理器架构

3.2 大规模模态并行求解体系



4 数值算例
4.1 某制动装备典型应用




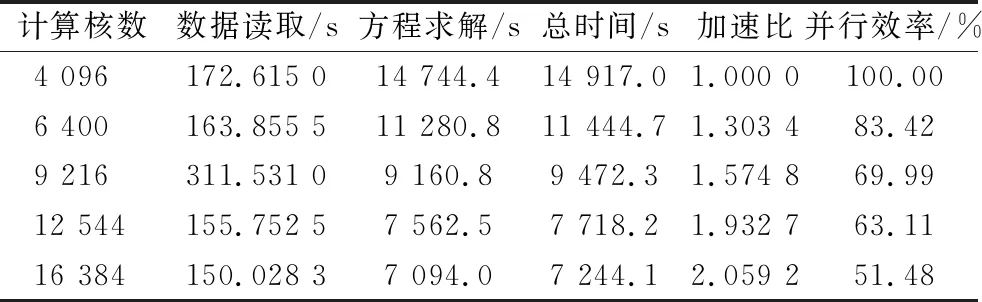
4.2 某跨江隧道典型应用

5 结 论
