基于有限元-向量式有限元的斜拉桥非线性振动计算方法

王 涛， 胡宇鹏， 张兴标， 刘德贵

(1.西南科技大学 土木工程与建筑学院，四川 绵阳 621000；2.中国工程物理研究院总体工程研究所，四川 绵阳 621999)

考虑几何非线性的数值计算方法在实际工程的分析中有重要的应用。陈政清等[1]详细研究了基于UL列式的非线性有限元(finite element,FE)法并将其运用到了桥梁工程的计算中。为了更简便地进行非线性有限元算法编程开发，依据Wempner[2]提出的随动坐标系格式方法(co-rotational formulation，CR列式)，邓继华等[3]开发了基于CR列式并考虑徐变作用的非线性杆、梁单元计算程序，应用到实际工程的静力计算中。 潘永仁[4]使用CR列式几何非线性算法开发了有限元计算程序，运用到大跨度悬索桥施工监控的静力计算中。

王涛等[5]研究开发了基于CR列式的动力非线性有限元方法，动力时程求解中使用了在Newmark-β算法下的Newton-Raphson隐式动力平衡迭代。该方法求解稳定性好，可以使用较大的时间积分步长，可以计算柔性结构的大幅度非线性振动。非线性动力有限元法在动力时程计算的每一步中都需要计算总体刚度、质量、阻尼矩阵集成切线刚度矩阵。由于隐式求解要求矩阵不能奇异，所以通常不能直接计算结构断裂、倒塌，破坏等无约束状态。

Ting等[6]提出了向量式有限元(vector form finite element，VFFE)的概念，丁承先等[7]详细论述了向量式有限元的特点。向量式有限元将结构视为在空间中通过单元联结成为一群质点集合，单元无质量，只视为质点相互关系的依据，质点运动满足牛顿第二定律。各个质点的内力、外力、加速度力依据单元联结信息分别集成为一组向量，使用显式的中心差分法得到结构动力计算结果。其优点在于，单元节点排序与计算规模无关。构件可以不限为杆件，可以处理大变形与大位移。在计算中可以改变结构单元的性质。由于不集成总体矩阵，可以在任意时刻切断单元联系，获得结构的断裂与倒塌行为。

关于向量式有限元，近几年各个学者进一步发展了其在结构工程中的应用。陈冲[8]使用向量式有限元模拟计算了大型网架结构的倒塌与破坏。王震等[9-10]基于向量式有限元思想，开发了计算程序，使用薄膜单元与四面体实体单元研究了结构的非线性受力行为以及破坏与穿透状态。曲激婷等[11]基于向量式有限元方法研究了黏滞阻尼减震结构抗竖向连续倒塌。Duan等[12]使用向量式有限元研究了列车-桥梁的耦合振动效应。李效民等[13]使用向量式有限元研究了浅海竖L型悬空管道三维动力响应。

离散元方法使用了更为一般的概念[14]，认为分析的结构对象是由一系列质点构成，质点之间的相互作用由接触力确定，在岩土工程中应用较多，可用于求解土体颗粒之间的相互作用，模拟堆积、塌方等工程现象。为了在结构工程中应用离散元方法，齐念等[15-16]建立了杆、梁结构的离散元，认为质点分布于单元节点上，质点之间的接触力以结构力学中杆、梁单元的计算公式来定义。在杆、梁结构的理论体系下，本文认为离散元与向量式有限元在算法本质上是一致的，同样是针对质点的求解，不需要组集总体刚度矩阵，使用显式数值积分计算结构动力问题，适合并行计算，叶继红等[17]开发了使用杆、梁离散元的GPU并行计算方法。

综上所述，本文认为，使用杆、梁力学模型的向量式有限元、离散元，结构构件的内力与外力计算方法上是一致的，是同一个方法的不同概念。所以，在后文中本文只讨论CR列式非线性有限元与向量式有限元的相同点与差别。

由于不组集总体刚度、质量矩阵，向量式有限元不能对结构进行模态计算。使用缓慢加载的显式动力积分来近似处理静力状态，得到结构自质量下的静力状态也较为麻烦。

本文使用了新的编程开发思路，基于核心原理的一致性，将有限元、向量式有限元纳入统一的程序框架。这样，避免了如丁承先等研究中专门针对某个问题编程的重复工作。使用通用的节点、单元、实常数、边界条件等的描述方法建立计算模型。使用非线性有限元方法计算结构的静力状态、动力特性，使用平衡迭代的有限元Newmark-β隐式方法计算结构长时间的非线性振动响应。通过直接设置调用向量式有限元求解模块，即可模拟计算结构的冲击、破坏、断裂等状态。本文方法弥补了有限元与向量式有限元各自的缺点，具有更好的适用性。

1 向量式有限元

如图1所示，一根梁单元在外力作用下，在t1时刻，单元1、2节点发生了位移和转动，经过Δt到达t2时刻变形状态。依据向量式有限元虚拟逆向运动的思想，假定X2Y2坐标系平移、旋转回到X1Y1坐标系的位置，两个坐标系重合，则X2Y2中梁发生的变化为单元的纯变形，这与CR列式非线性有限元方法通过扣除刚体转动得到单元的实际变形状态想法是完全一致的。单元节点位置即为向量式有限元的质点。

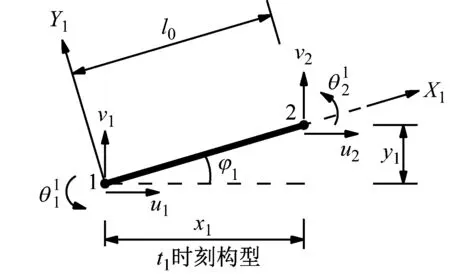
(a)

使用向量式有限元的求解规则如下。

(1) 梁的纯变形。为了求解梁的纯变形，令t1时刻单元做逆向的平移与转动，使t1时刻单元的节点1与t0时刻单元重合，X2Y2与X1Y1方向重合。忽略单元的弦向变形，单元的伸长使用轴向变形来描述

Δl=l1-l0

(1)

单元逆向转动的转角为

Δφ=φ2-φ1

(2)

可以得到单元的实际转角为

(3)

t1与t2时刻转角的增量

(4)

(2) 单元内力计算。向量式有限元将运动历程划分为一系列途径单元。在同一途径单元内，内力计算以本时刻t1与下一个时刻t2构型为基础。依据结构力学原理可以求得各个节点在局部坐标系下的内力增量。

(5)

式中,E、A、I为单元在t2时刻的材料切线模量、单元面积、为单元截面惯性矩。依据向量式有限元的思想，内力增量在结构变形的任意时刻t1都可以变化的。

考虑单元静力平衡条件可以计算出节点内力为

ΣFx=0,f1x=-f2x

(6)

ΣFy=0,f1y=-f2y

使用坐标转换可以得到全局坐标系下的单元的节点内力即

(7)

式中:Fi为总体坐标系下的节点内力向量；R为t2时刻总体坐标系到单元局部坐标系的坐标转换矩阵；如图1所示，倾角为φ2，所以

(8)

(3) 运动公式。 根据牛顿第二定律，点i的运动公式如下

(9)

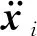
(4) 求解方法。使用向量式有限元不需要组集总体刚度矩阵，通过结构模型单元连接信息集成总体内力向量F、外力向量P、质量向量m、位移向量x。向量式有限元一般使用中心差分法显式求解，当考虑阻尼时，由中心差分公式得到

xn=Clh2m-1F+2C1xn-1-C2xn-2

(10)

式中:C1=1/(1+0.5ξh);C2=C2/(1-0.5ξh);ξ为阻尼比;h为积分时间步长。由式(1)～式(9)可知，向量式有限元直接建立了结构的外力向量、内力向量、加速度力向量的对应关系，使用显式动力学积分，不求解矩阵方程，不存在有限元方法中矩阵奇异问题。向量式有限元求解规模与节点数量相关，与节点排序无关。

(5) 向量式有限元求解基本流程,如图2所示。

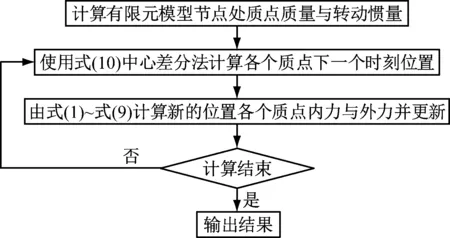
图2 向量式有限元计算流程

(6) 断裂模式。在丁承先等、陈冲、王震等的研究中将断裂模式设置为在模型节点处断开，单元数量不变，但这会导致计算中临时增加节点，对编程不利。可以参考杆梁结构离散元模式将单元划分更为密集，当单元力大于或定义某个时刻的时候，直接把单元力置为零，即可模拟断裂情况。这时在单元处断开不需要随时间增加节点力向量，虽然增加了计算量，但能更符合实际情况。

(7) 碰撞检测。结构断裂后的构件可以自由运动，可能与其他构件或掉落地面发生碰撞。碰撞须满足动量守恒与能量守恒定律。质点碰撞后对当前时间步质点的速度进行修正计算，在后续计算中若不发生碰撞，继续使用式(10)计算，若检测到碰撞则继续修正速度。具体方法可参考陈冲的研究。

2 基于CR列式的非线性隐式有限元动力时程计算方法

依据参考潘永仁、王涛等的研究，本文作者开发了基于CR列式的非线性静力、动力有限元算法。对于非线性有限元静力计算，结构的总体的计算公式为

F(x)=P(x)

(11)

式中:F为结构内力向量;P为结构外力向量;它们都与节点位移x相关。可以使用单元刚度矩阵组集结构总体切线刚度矩阵，使用Newton-Raphson方法进行平衡迭代得到结构的静力平衡状态。

对于每个二维梁单元，单元坐标系称为随动坐标，根据单元位置实时计算，单元的实际内力计算与向量式有限元思想相同，通过扣除刚体位移，得到单元实际位移向量。

xe={0 0θ1u120θ2}T

(12)

式中:θ为扣除刚体位移后，单元坐标系下实际转角;u12为单元的伸长。计算方式与向量式有限元相同，依据有限元法规则，与式(5)的力学意义相同，使用单元刚度矩阵ke直接乘以单元位移向量

fe=kexe

(13)

得到单元的内力向量fe。与式(7)相同，依据当前时刻单元位置，使用单元随动坐标系下的坐标转换矩阵Te可得到总体坐标系下结构各个节点内力向量F与外力向量P。关于二维梁单元的刚度矩阵、坐标转换矩阵等计算原理可以参考有限元方法文献[18]。

对于动力求解问题，参考王涛等研究所述的详细研究开发过程。基于CR列式考虑几何非线性时，由t1时刻经过Δt结构t2时刻的振动方程为

(14)

式中：M为总体质量矩阵；C为总体阻尼矩阵；F为结构内力向量；P为结构外力向量。依据Newmark-β法设定t1、t2时刻位移、速度、加速度之间的关系为

(15)

(16)

式中，a0～a5为积分参数，将式(15)代入式(14)得到

(a0M+a1C)x(t2)+F[x(t2)]=P[x(t2)]+

(17)

在每一个积分时间步内求解非线性方程式(17)即可得到结构的非线性振动时程，式(17)左右端都与各个节点当前位移向量x(t)相关。式(17)左端记为结构等效内力向量F，右端记为结构等效外力向量P。在计算结构总体切线刚度矩阵后，即可使用Newton-Raphson法迭代求解。

根据以上论述，可知依据CR列式的静、动力非线性有限元方法在结构的单元节点内力与外力以及坐标转换的计算方法与向量式有限元完全一致。不同点在于，CR列式非线性有限元有限元法中，静力使用内外力平衡迭代求解，动力是在Newmark-β算法框架下进行平衡迭代，为有限元隐式方法。而向量式有限元本质上是基于单元随动坐标系考虑几何非线性的显式有限元动力时程积分。

3 有限元-向量式有限元统一算法框架

CR列式非线性Newmark-β隐式方法具有较好的收敛性与计算稳定性，可以使用较长的时间步长，可以较好地模拟结构低频非线性振动响应。而向量式有限元不集成总体刚度矩阵，使用显式动力学积分计算，通常使用较小的时间步长，可以获得结构在短时间内受到冲击、断裂状态下的动力响应。本文开发的有限元-向量式有限元统一程序框架,如图3所示。

如图3所示，向量式有限元在计算单元内力与外力时可以与CR列式的非线性有限元动力时程积分共用计算模块。使用有限元-向量式有限元统一的算法框架，无需如丁承先等研究中那样针对每个结构问题进行单独地向量分析与建模编程。程序中只需建立有限元几何模型，然后根据计算需要选择进入向量式有限元计算流程即可。

在结构的动力分析中，通常需要首先得到结构在自质量下的静力状态。向量式有限元是不组集总体刚度、质量矩阵的显式动力计算，计算结构静力状态时，需设定适当的耗散阻尼，使用缓慢加载来模拟静力过程，过程相对较为繁复，也无法进行模态计算。所以，如图3所示，本文使用该程序的分析流程为：首先，使用非线性有限元计算得到结构的静力状态；然后计算结构模态；最后再根据分析对象的实际情况选择使用有限元或向量式有限元计算结构的非线性振动状态。

向量式有限元为显式积分方法，计算过程中无隐式积分那样使用平衡迭代在每一步迭代中检查收敛性，即：每一步均检查式(17)中左端等效内力与右端等效外力是否达到平衡状态。因此，算法的严谨性相对较为欠缺，时间步长的选取对计算结果影响较为明显。可以使用隐式方法来验证向量式有限元求解时间步长的可靠性。

4 算例验证

依据第1～第3章所述原理开发了有限元-向量式有限元的相关算例，为了与向量式有限元保持一致，有限元计算中使用集中质量矩阵。

4.1 弹簧摆自由振动断裂后自由落体以及碰撞(算例1)

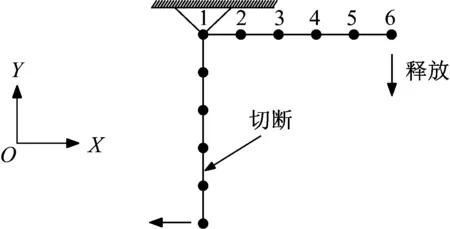
图4 弹簧摆自由振动模型

图3 有限元-向量式有限元统一算法框架流程图

Fig.3 The flow chart of finite element & vector form finite element method unified algorithm framework

弹簧摆使用杆单元模拟，质量分布在节点上。单元弹性模量E=100 Pa，截面积A=1.0 m2，质量密度ρ=1.0 kg/m3，重力加速度G=9.8 m/s2，单元初始轴力为50 N，向量式有限元设置阻尼比ξ=0.2，计算时间步长h=0.000 1 s，求解50 000步，假设断裂部分自由落体与地面接触后碰撞竖向的速度全部反弹。

使用本文程序建立有限元模型，首先，使用非线性有限元静力计算程序得到结构的初始构型，然后使用向量式有限元计算模块得到结构的运动轨迹(动画)如图5所示。

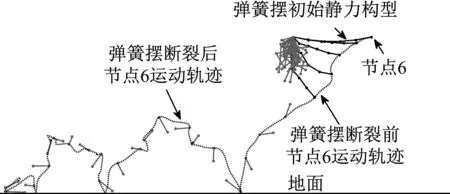
图5 弹簧摆自由振动的运动轨迹

Fig.5 The time-history of free vibration of the spring pendulum

从图5可知，计算中弹簧摆首先使用有限元法得到了静力状态初始构型，释放后发生了非线性自由振动，当单元4断裂后，端部一个单元自由落体与地面发生了碰撞并反弹，图中虚线为节点6运动的轨迹线。

得到节点6以及节点4的动力时程响应曲线,如图6所示。

由图5与图6可知，向量式有限元较好地模拟了弹簧摆的运动过程。

(a) Y方向位移时程曲线

4.2 索梁组合结构非线性振动(算例2)

桥梁工程中常见的索-梁组合结构简化模型有限元模型的几何尺寸,如图7所示。

(2) 从实验和数值角度研究了0Cr18Ni9不锈钢材料实际的起裂断裂韧度，针对I型裂纹紧凑拉伸测试，利用扫描电镜断面观察和声发射技术确定起裂载荷为23kN，根据不同方法所计算的J积分存在差异性。按照GB/T 21143标准计算的J积分的实际起裂断裂韧度值JiGB为351.4kJ/m2，处于有限元计算的J积分范围内。利用数字图像相关方法测量的位移场计算得到的实际起裂韧度值JiDic(293.4kJ/m2)与有限元计算的J积分平均值JiFem(293.1kJ/m2)接近。

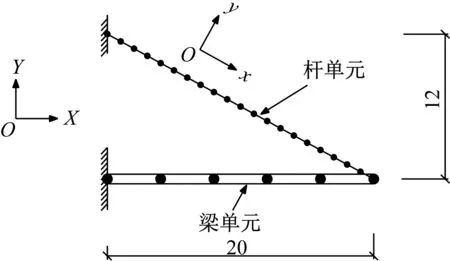
图7 索-梁组合结构有限元-向量式有限元公用模型(m)

总体坐标系为XY，建立拉索模型局部坐标系为X1Y1。梁分为5个二维梁单元，拉索共分为20个二维直杆单元。不计泊松比，梁单元的物理参数为，弹性模量E=2.0×1011Pa，剪切模量G=1.0×1011Pa，材料质量密度ρ=7 800 kg/m3，单元截面积A=0.045 m2，抗弯惯性矩Iz=1.7×10-3m4。杆单元弹性模量、质量密度与梁单元相同，截面积A=3.0×10-4m2初始轴力H=5.0×104N。

向量式有限元算法无法计算结构自振频率。所以，首先，使用非线性有限元计算结构的静力状态。然后，对结构进行模态计算。结构自振频率与振型,如图8所示。

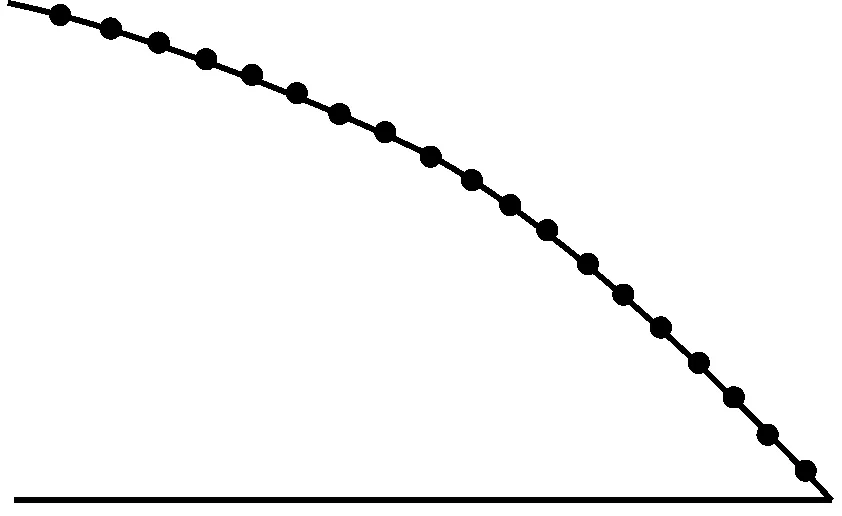
(a) 第1阶频率:3.135 9 Hz

本算例对拉索的索力以及结构的总体刚度进行了设计，所以，模态计算结果表明，结构的1阶、2阶模态中可以看到拉索和整体结构同时发生振动的振型。依据Nayfeh等[19]的研究可以知道，在外激励作用下，拉索会在梁的带动下发生1阶共振。

先进行静力计算，然后在图6的梁端点处施加Y方向外力-10 kN，然后释放，使用本文开发的非线性有限元-向量式有限元计算得到拉索1/2点振动时程曲线如图9所示。其中非线性有限元Newmark-β动力时程积分步长为0.001 s，向量式有限元非线性显式动力学积分时间步长为0.000 1 s。

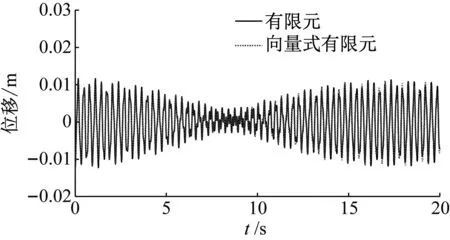
(a) 梁端点振动时程图

由图9可知，梁端受到集中力变形后，索-梁组合结构发生了自由振动，由于拉索局部频率与整体结构频率接近。振动能量在拉索和梁之间传递，梁与拉索的振幅呈现“此消彼长”的状态。由频谱图可以看出，梁的结构的响应频率3.15 Hz幅值较大8.60 Hz幅值较大，索的主要响应频率为3.20 Hz。与计算得到的自振频率接近，这说明，由于结构振幅较小，为弱非线性振动，接近线性振动响应。有限元与向量式有限元计算结果一致。

为了对比结构在较强非线性振动状态下，两种计算方法的计算结果。不设置阻尼，在图7模型梁右端部作用沿y方向的竖向简谐力P=P0sin(ωt)，其中外力项P0分别取-1.0 kN、-2.0 kN、-3.0 kN，激励频率ω取3.16 Hz。结果如图10所示。

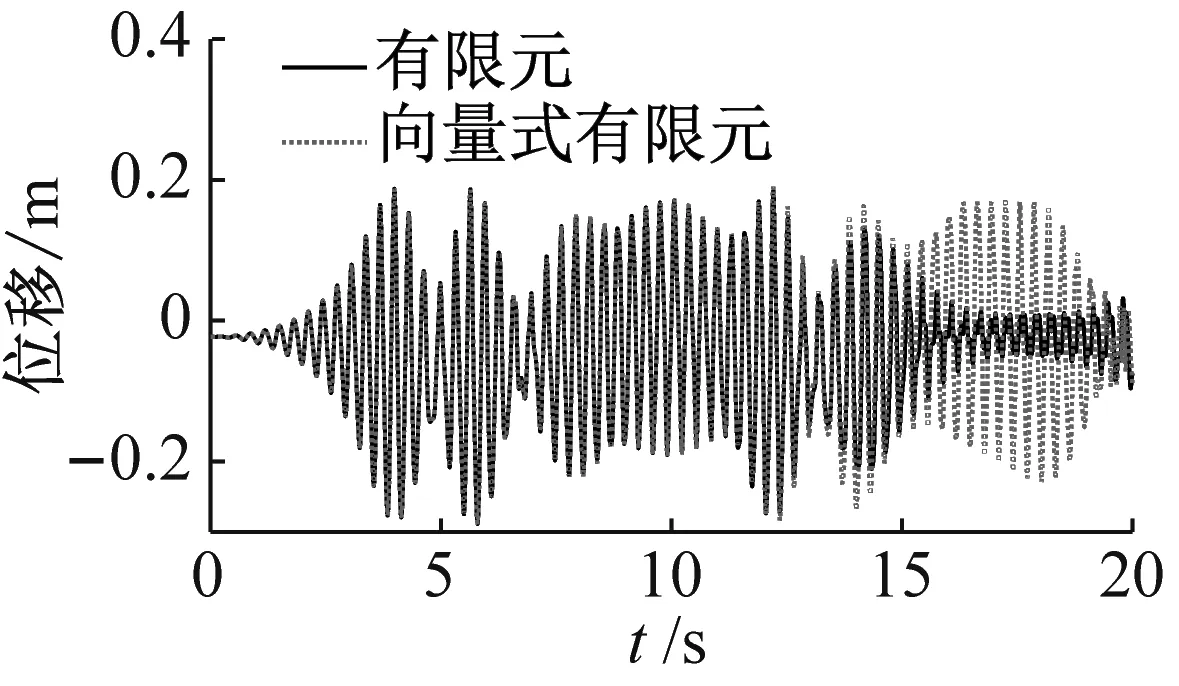
(a) 振动时程图(P0=-1.0 kN)

由图10可知，由于外激励与整体结构以及拉索的频率接近(3.136 Hz)，结构发生了共振。虽然未设置阻尼，但由于非线性振动效应导致的“振动硬化”现象，拉索的振幅不会一直增加，而是呈现了“拍振”的状态，由图10(b)可以看出，拉索发生了非线性振动，结构的响应频率发生了改变，变得更加复杂，结构响应频率的复杂度与振幅相关。关于非线性振动现象的更多理论解释，可以参考Nayfeh等的经典著作。

观察图10(a)可以看出，分别使用有限元与向量式有限元计算，振动发展的初期，两者计算结果时程曲线是重合的。但随着振动的发展，差别相对变得明显，依据Nayfeh等的研究，这是由于非线性振动对初始条件敏感决定的，微小的初始条件差别会随着振动发展非线性增加。本文有限元、向量式有限元结构内力、外力计算方法相同，但由于动力算法的差别(隐式、显式算法)，导致了振动时程图差别随时间发展逐渐明显。

从各个频谱图可以看出，两种计算结果的频率响应趋势是接近的，都呈现了非线性振动导致的响应频率复杂化状态。外力P0取值越大，频谱图中得到的结构频率响应越复杂，振动非线性的程度越大。由时程图可以看出，当P0分别为-1.0 kN、-2.0 kN、-3.0 kN时，时程曲线开始产生差别的时间分别约为第15秒、10秒、4秒。这说明非线性程度越大，非线性振动造成的差别放大效应越明显，这符合非线性动力系统的特性。

综上所述，本算例使用向量式有限元得到了结构非线性振动的结果，与CR列式非线性有限元对比，验证了向量式有限元法的合理性与可靠性。

5 基于有限元-向量式有限元的车-桥耦合动力作用下斜拉桥非线性振动分析

缆索承重结构的断索状态分析是近期工程结构研究中的热点内容。张超等[20]研究了多重四边形环索-张弦穹顶局部断索冲击，对于拉索断裂模拟，使用了单元退出工作的等效荷载瞬时卸载法。张羽等[21]研究了大跨混凝土斜拉桥施工过程中结构的断索后的受力状态，基于ABAQUS有限元软件，使用静力计算后瞬时拆除构件方法进行了研究。Zhou等[22]使用结构模型单元状态迭代更新的等效荷载法，基于SAP2000有限元程序，开发了复杂的算法流程，分析了汽车作用下拉索断裂时斜拉桥的非线性振动状态。

以上研究中均采用了商业有限元程序进行研究，要得到合理的计算结果，技术上处理较为复杂。而使用本研究开发的有限元-向量式有限元统一算法框架，由于向量式有限元使用显式动力时程计算的特性，可直接进行动态模拟，不需要进行复杂的几何模型处理、受力边界条件处理。只需要设定拉索断裂的时间或受力条件，程序可以自动运行，达到条件即将单元内力置零来模拟拉索断裂，可以方便地直接计算得到斜拉桥拉索断裂时的非线性振动状态，同时得到断裂拉索在重力作用下的自由坠落状态及其与桥梁结构可能发生的碰撞。

参考李永乐[23]所述列车-桥梁耦合动力作用计算方法以及秦顺全[24]研究中的研究数据，以天兴洲长江大桥为研究对象，建立二维简化计算模型,如图11所示。

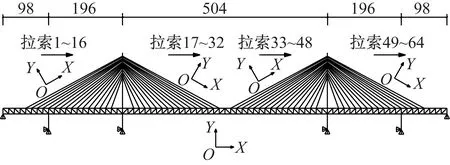
图11 天兴洲长江大桥二维模型(m)

总体坐标系为XY，X为纵向，Y为竖向。斜拉桥为3索面，所以二维模型参数按照1/3简化，各个拉索的编号如图11所示。桥塔上靠近中跨、边跨最长的3根拉索分为40段，其他拉索分为20段。 全桥共1 221个节点，1 433个单元。斜拉桥主梁端部竖向约束，主梁与辅助墩为竖向约束连接，主梁与桥塔横梁位置为竖向约束连接，纵向使用弹性阻尼连接模拟纵向液压阻尼器的约束。重力加速度取G=9.8 m/s2。阻尼比设为0.05%。计算列车使用二维4轴模型如图12所示。

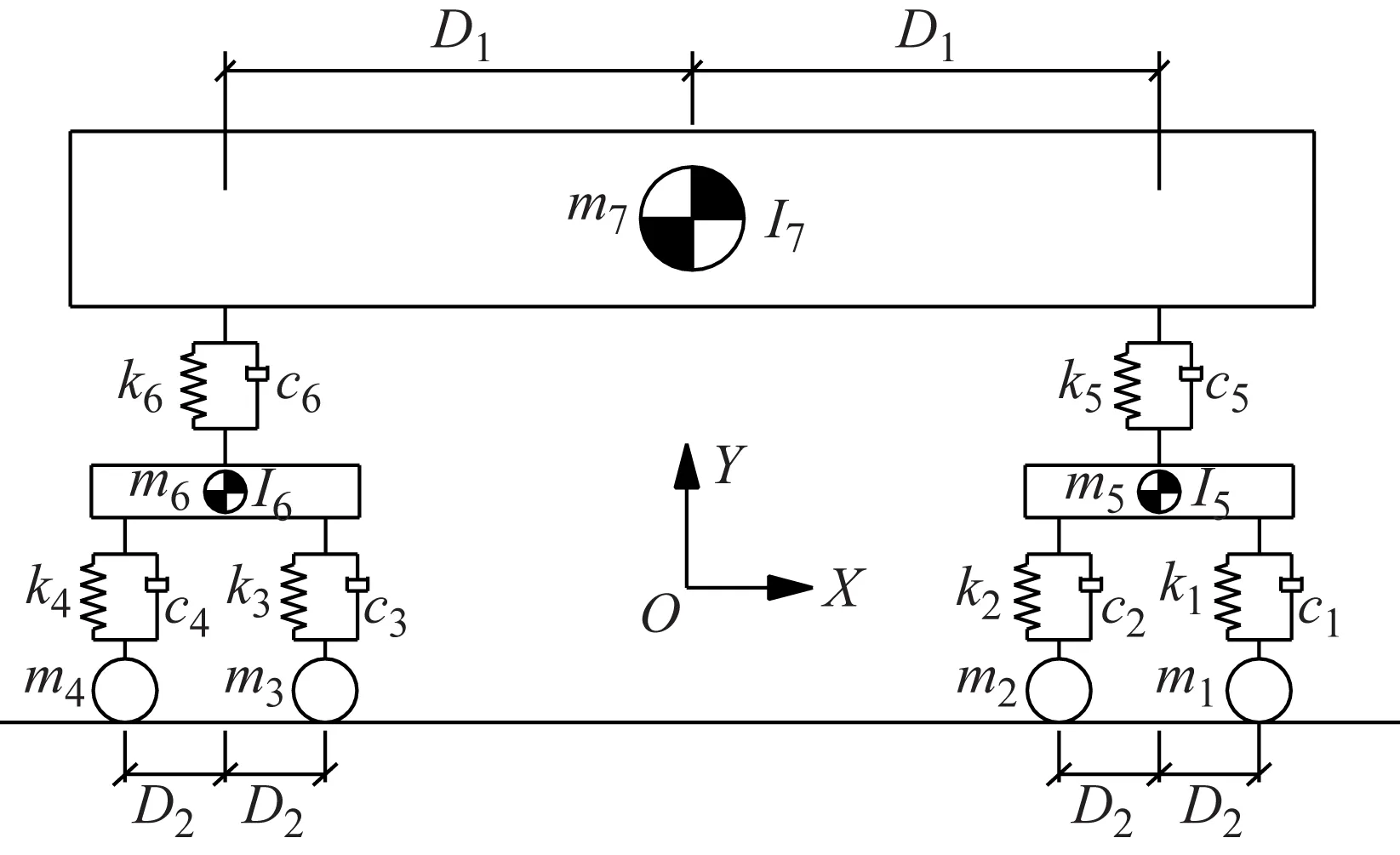
图12 一节列车车厢模型

高速列车的刚度、阻尼、质量参数使用CHR2动车组，一列列车共8节车厢，与桥梁相同，也按照1/3简化。轨道不平顺使用德国谱低干扰谱模拟。使用车、桥系统分离迭代方法计算列车、桥梁相互作用力。

使用非线性有限元计算结构在自质量作用下的静力构型，再计算得到全桥前2阶自振频率如图13所示。

由图13可知，第1阶为全桥振动模态，第2阶为拉索局部振动模态。全桥模型与拉索的局部频率有明显差别，根据王涛[25]的研究，在日常运营中，列车作用下斜拉桥不会在端部位移激励下发生共振。

(a)

使用线性、非线有限元、向量式有限元分别计算一列列车过桥，计算结果如图14所示。其中，列车速度为200 km/h，列车第1轮对进入桥梁开始计算，总共运行1 400 m。有限元计算使用空间步长0.25 m换算得到时间0.004 5 s，计算步数为5 600步。向量式有限元时间步长取0.000 1 s，列车运行距离换算为计算步数为252 000步。

(a) 主梁1/2点Y方向振动时程

由图14可知，分别使用3种计算方法，得到的计算结果差别很小，其中线性、非线性有限元计算结果有微小差别，非线性有限元与向量式有限元计算结果一致，这是由于列车过桥时桥梁受力接近一个静力过程，且非线性程度很小的原因。

依据前期各个研究，斜拉桥拉索受到火灾或疲劳破坏通常更容易在端部断裂。所以，这里在计算斜拉桥静力状态后，假设拉索32靠近主梁端部附近突然发生断裂，使用向量式有限元计算，计算中不考虑拉索断裂后的碰撞。在计算开始1 s后拉索发生断裂，向量式有限元计算时间步长为0.000 1 s。总共计算25 s得到计算结果，如图15所示。

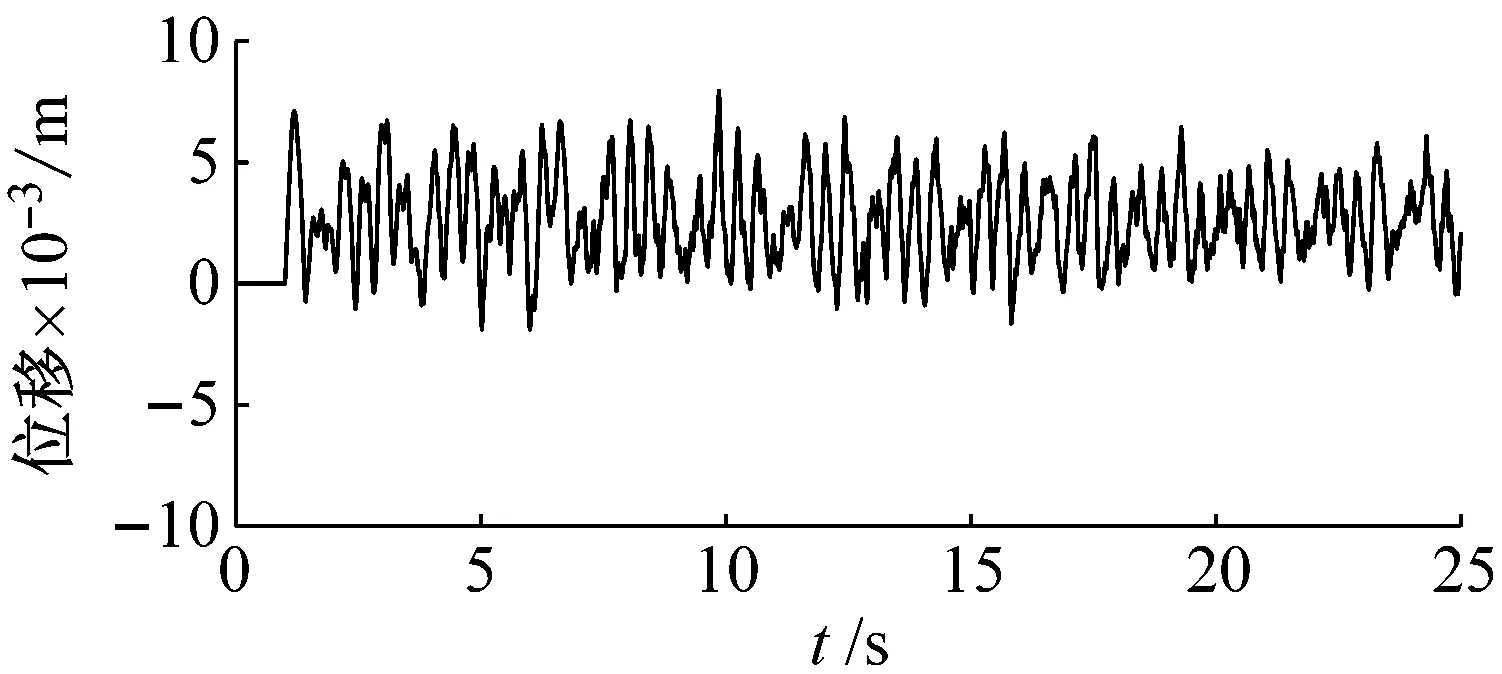
(a) 主梁1/2点X方向振动时程图

由图15(a)可知，主梁发生了明显纵向(X方向)振动，振幅在0.01 m以下，由于跨中左侧最长拉索发生断裂，所以振动的平衡位置为正方向。主梁与桥塔之间存在竖向支撑同时设置了纵向弹性液压阻尼器，所以纵向响应幅值较小，且随时间衰减。主梁1/2点竖向(Y方向)振幅约为0.2 m。由图15(c)可知，拉索32在重力作用下发生了大幅度非线性下坠振动(不计碰撞)。由图15(d)可知拉索第6秒的下坠状态。

为了研究拉索断裂对高速列车行驶安全性的影响。假定拉索断裂时列车仍然沿轨道在桥面上行驶，当列车作用以200 km/h速度通过斜拉桥，使主梁1/2点位移达到最大时，拉索32靠主梁端部突然发生断裂，得到计算结果如图16所示。

由图16(a)可知，拉索32断裂时，斜拉桥主梁1/2点发生了明显的较大幅度竖向振动，由于列车作用在桥梁上，振幅较图15(b)更大。

由于这里假设列车始终在桥梁的轨道上行驶，观察图16(b)可知，当拉索发生断裂时，列车的竖向振动幅值突然最大增加约0.2 m。观察图16(c)，列车的竖向加速度由约0.4 m/s2突然增大至接近4.0 m/s2。依据李永乐提供的研究数据，列车过桥的竖向加速度需小于3.63 m/s2。显然，列车车厢竖向的位移、加速度值的突变会使列车乘客产生较大恐慌，拉索32的突然断裂会对列车的行驶安全性造成威胁。

(a) 主梁1/2点Y方向振动时程图

得到列车过桥拉索断裂时各个拉索的索力变化结果,如图17所示。

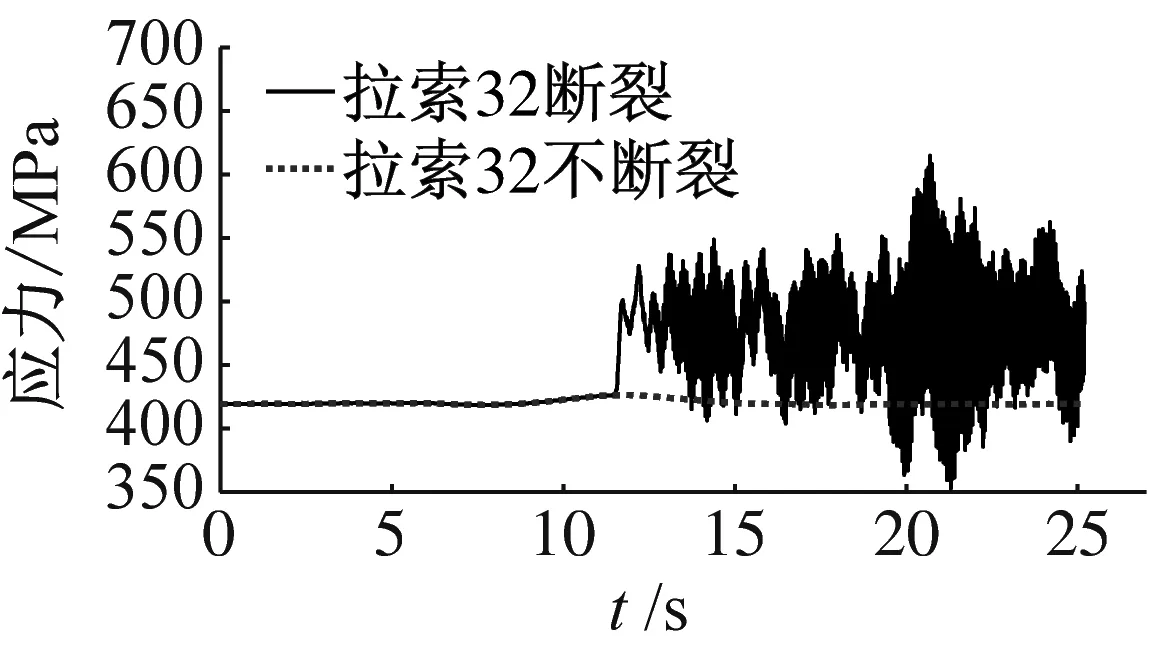
(a) 拉索31应力时程图

由图17可知，当高速列车过桥运行至跨中时若拉索32发生断裂，拉索31的应力幅值相对较大，而右半跨的跨中拉索33以及左半跨跨中靠桥塔拉索17的应力幅值相对较小，但拉索承受的最大应力的均远小于拉索设计极限强度1 860 MPa。

这说明，对于斜拉桥这个较为复杂的多自由度结构体系，少量拉索断裂后，其他拉索能够有效分散承担结构受到的外部荷载与结构自质量，离断裂拉索越远的拉索受到的影响相对越小，所以，本文认为，列车过桥拉索32断裂时，桥梁结构是相对较为安全的。

6 结 论

(1) 基于随动坐标系(CR列式)的动力非线性Newmark-β有限元法为使用平衡迭代的隐式动力时程积分方法。而向量式有限元法本质上是CR列式几何非线性有限元显式动力时程积分方法。

(2) 有限元通常无法直接计算结构受到破坏、断裂、无约束等非线性动力状态，向量式有限元可以模拟结构的断裂、破坏、碰撞等非线性动力响应，但无法进行直接静力计算、结构模态计算。基于核心原理的一致性，本文开发了有限元-向量式有限元统一算法框架，弥补了这两种方法各自的缺点。

(3) 对于大跨度斜拉桥，使用本文的有限元-向量式有限元结合的方法能更好地对结构进行全面的计算分析。对于列车-桥梁耦合振动，使用非线性有限元与向量式有限元的计算结果是一致的。本文研究表明：当高速列车运行通过斜拉桥时，若跨中最长拉索突然发生断裂，斜拉桥主梁会发生较大幅度振动，对桥梁结构的安全性影响相对不大，但会对列车的行驶安全性造成威胁。

(4) 向量式有限元可以直接计算斜拉桥在极端情况下的非线性振动。计划在后续研究中进一步开发使用杆、梁单元的三维空间向量式有限元算法程序，针对实际斜拉桥增加更多极端作用下的计算工况，为实际斜拉桥在动力破坏状态下的安全性评估提供研究依据。