基于遗传神经网络的履带行驶系统载荷识别方法

2022-02-22张志宏李国华

振动与冲击 2022年3期

张志宏，张宏，陈有，李直，李国华，付政

(太原科技大学机械工程学院，太原 030024)

履带行驶系统广泛应用于煤矿机械设备中[1]，其主要承载部件履带板和链板间销轴承受不同的挤压、弯曲等应力，很容易造成链板间销轴的断裂[2]，而且煤矿掘进机器人履带行驶系统工作环境恶劣，长期作业于积水、非结构化地形和封闭受限环境中，链板间拉力无法直接测得。

目前，对履带行驶系统的研究主要采用理论分析和数值模拟的手段[3-4]。金守峰[5]利用磨损过程离散和协同仿真技术实现了连续采煤机履带销-销耳的动态磨损预测。姚继权等[6]结合拉格朗日第二类方程与离散体动力学模型法，建立了掘进机履带行驶系统的动力学微分方程，对链板间拉力波动情况进行了分析。王锦红等[7]针对履带行驶系统在海底运行时不同类型的地形环境，对驱动轮和履带销啮合力进行分析。Jiang[8]对履带行驶系统前进后退两种工况进行仿真，分析比较了恒速和恒转矩两种情况下驱动轮与履带板的啮合力。然而在实际中，受复杂环境和经济因素的限制，履带行驶系统动载荷无法直接测得，需要通过反映机构振动特征的物理量间接识别应力载荷。很多学者提出了正则化技术，高伟等[9]采用L∞范数拟合正则化方法结合积分滑动平均进行动态载荷识别。周玙等[10]提出基于应变响应的瞬态正则化载荷识别方法。王能建等[11]提出了新型分数阶Tikhonov正则化载荷重构技术。除此之外，张玉良等[12]利用频响函数矩阵求逆法进行冲击载荷识别。Sun等[13]提出了一种基于移动加权最小二乘法的动态载荷时域识别方法。Wang等[14]通过最小化误差函数来解决动载荷识别的不适定问题，提出新的共轭梯度法来识别多源动态载荷。Kim等[15]提出用奇异值分解法解决非最小相位系统的反问题。张猛等[16]结合Tikhonov正则法与粒子群优化算法对载荷识别数学模型进行求解。Zhou等[17]提出了深度递归神经网络对非线性结构冲击载荷识别的方法。Marano等[18]提出了迁移策略、自适应再生算子和搜索空间缩减技术相结合的多种群遗传算法用于识别大型机械系统的动载荷。上述研究对履带行驶系统在理论、动力学仿真以及载荷识别方法的选择起到了指导作用，但对于履带行驶系统间接载荷识别的研究仍缺乏必要的试验数据支撑，载荷识别精度难以得到验证。

本文以履带小车为研究对象，开展了GA-BP(genetic algorithm-back propagation)神经网络载荷识别方法的研究，该方法利用神经网络模型表示结构动力学系统的灰箱，针对神经网络易陷于局部最优解的问题，用遗传算法对其优化。借助小波变换和滤波技术对信号进行处理以提高载荷识别精度，最后通过试验验证了该方法在载荷识别中的有效性。

1 GA-BP神经网络载荷识别模型建立

1.1 履带行驶系统载荷识别理论

载荷识别是结构动力学中的一类反问题。在煤矿机械中，由于复杂环境和经济因素的限制，直接测试动载荷非常困难，而结构的振动信号却很容易测得。因此，在零初始条件下，通过脉冲响应函数建立振动信号与应力载荷之间的关系。

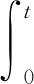
(1)

式中：y(t)为结构的振动信号；p(τ)为τ时刻应力载荷值；h(t-τ)为单位脉冲响应。

假设履带行驶系统沿纵轴左右对称，侧摆振动忽略不计，只考虑系统线性振动。以履带行驶系统驱动轮为研究对象，忽略与驱动轮接触的履带质量及履带厚度，对驱动轮受力分析如图1所示。

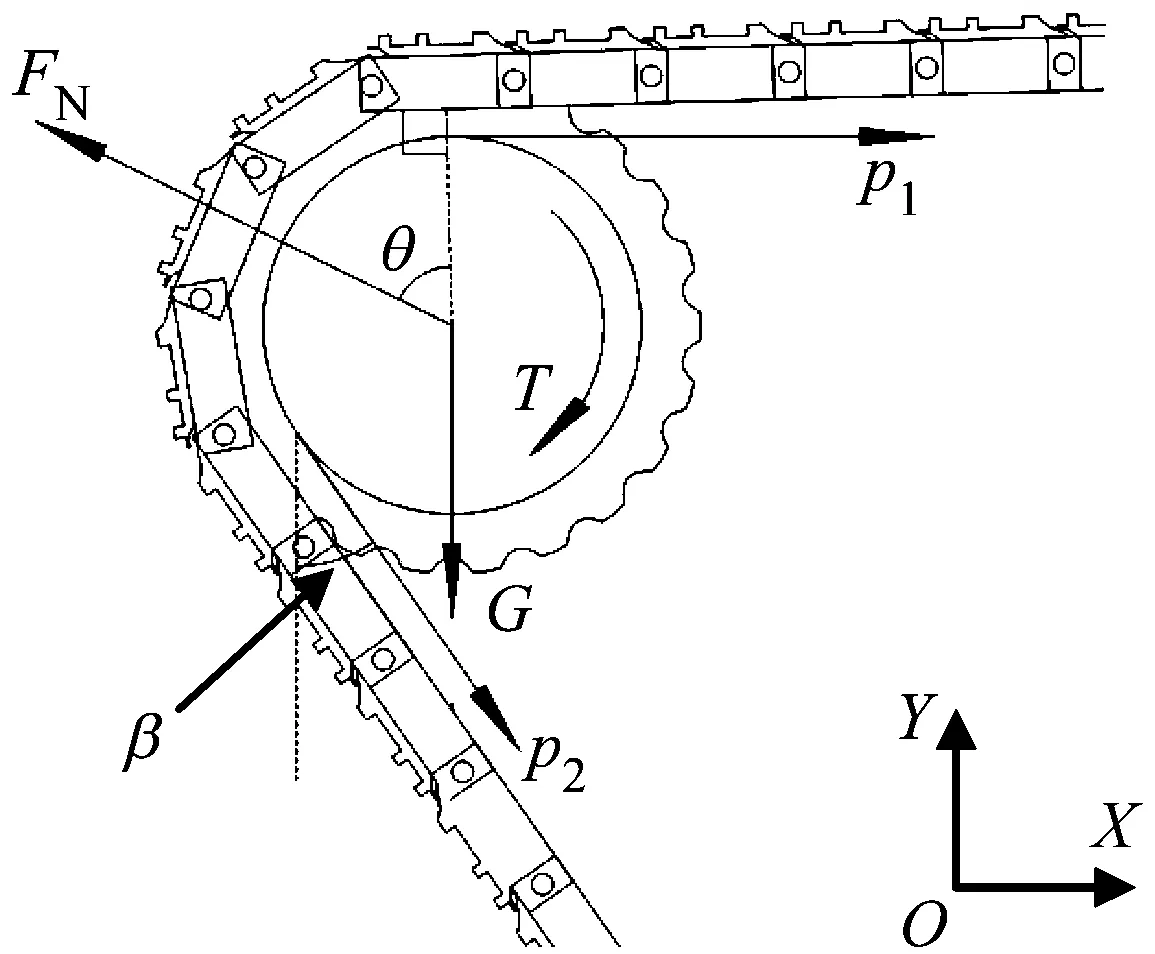
图1 履带行驶系统驱动轮受力分析

根据力平衡方程得到驱动轮的受力方程见下式

(2)

(3)

Jα=T-(p2-p1)r

(4)

式中：p2为工作支段拉力；p1为自由支段拉力；FN为驱动轮受到的支持力；β为工作支段拉力与竖直方向的夹角；θ为支持力与竖直方向的夹角；T为驱动轮的驱动力矩；J为驱动轮转动惯量；α为驱动轮转动角加速度；r为驱动轮半径。

履带行驶系统中，工作支段的拉力包括自由支段的拉力和工作拉力[19]。

p2=p1+p0

(5)

式中，p0为工作拉力，由车辆运动条件决定，等于履带运动阻力或车辆牵引力的一半。

通过式(2)～式(5)，可得到履带行驶系统自由支段拉力与振动加速度关系

(6)

该力学模型揭示了理想情况下履带行驶系统链板间拉力与振动加速度存在一定的关系，然而在实际中，当结构不满足线性和时不变假设时，式(6)不能完全适用，但对于实际履带行驶系统响应与应力载荷之间关系的建立提供了指导作用。响应与应力载荷之间总会存在一个关系Fi,j，使式(7)成立

(7)

(8)

1.2 BP神经网络设计

BP(back propagation)神经网络是神经网络中应用最广泛的一种多层前馈型网络，通过误差反向传播不断修正各层的权值和阈值，当达到最大训练次数或训练目标时，停止训练并输出预测结果。根据Kolmogorov定理，任一连续函数可由一个3层前馈网络逼近，逼近情况由网络结构和学习算法决定[20]，3层的网络拓扑结构图，如图2所示。

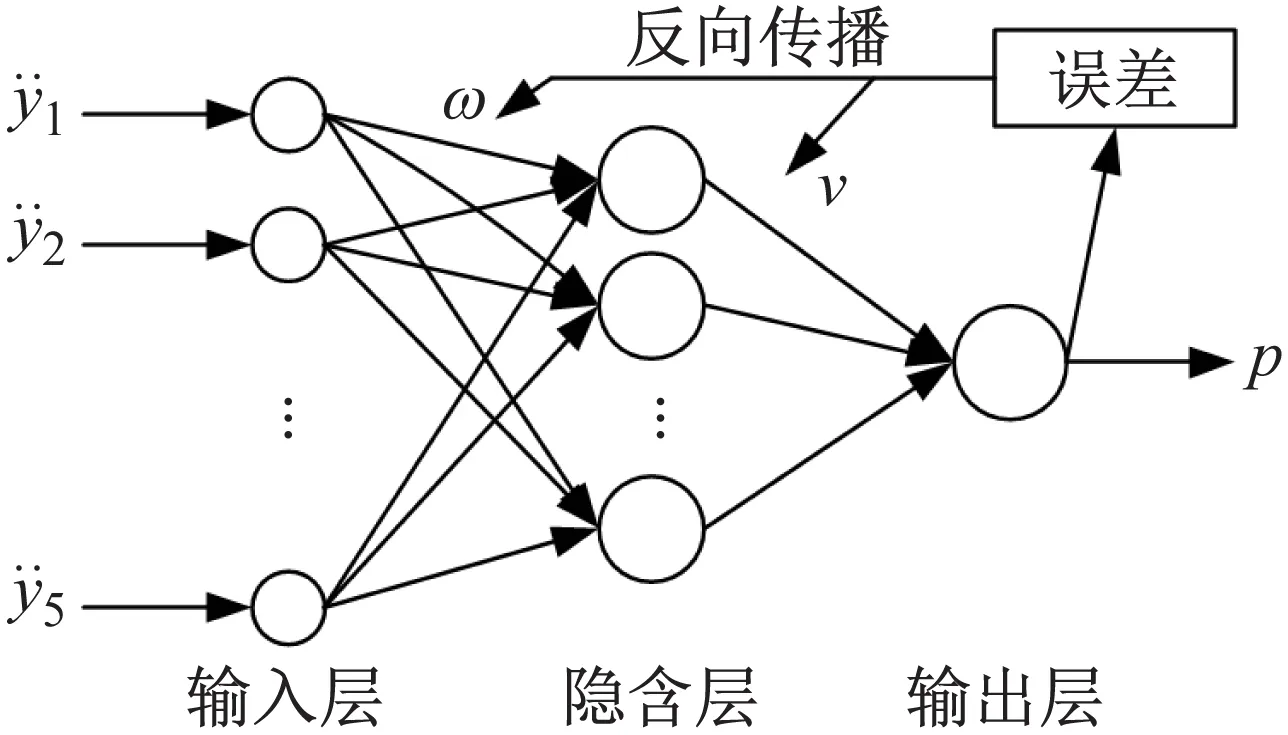
图2 BP神经网络结构示意图

(9)

(10)

式中：bt为隐含层第t个神经元的输出；θt为隐含层第t个神经元的阈值；γ为输出层的阈值；q为隐含层神经元个数。

BP神经网络训练算法为Levenberg-Marquardt，该算法最大的缺陷是容易陷于局部最优，使得BP神经网络预测精度在实际应用中不能很好的满足需要。

1.3 遗传算法设计

遗传算法(genetic algorithm,GA)基本要素包括：种群初始化、遗传操作和适应度函数确定。本文遗传算法采用浮点编码产生初始种群，浮点编码在遗传算子选择上更广泛，而算法的收敛速度取决于遗传算子的选择。遗传算子分别为轮盘赌选择法、算术交叉和非均匀变异。适应度函数作为GA的评价准则，适应度值越高，越接近最优解，个体更容易保留下来。本文适应度函数根据BP网络的训练误差平方和确定。误差平方和越小，适应度越大。所以适应度函数根据下式确定

(11)

val=1/E

(12)

式中：E为误差平方和；Tk和Yk为神经网络第k个训练样本的期望输出与实际输出；val为适应度函数；n为神经网络训练样本个数。

遗传算法具体优化过程，如图3所示。对BP神经网络的初始权值和阈值进行编码产生初始种群，BP神经网络训练误差的平方和倒数作为适应度函数，通过选择、交叉、变异寻找最优个体。

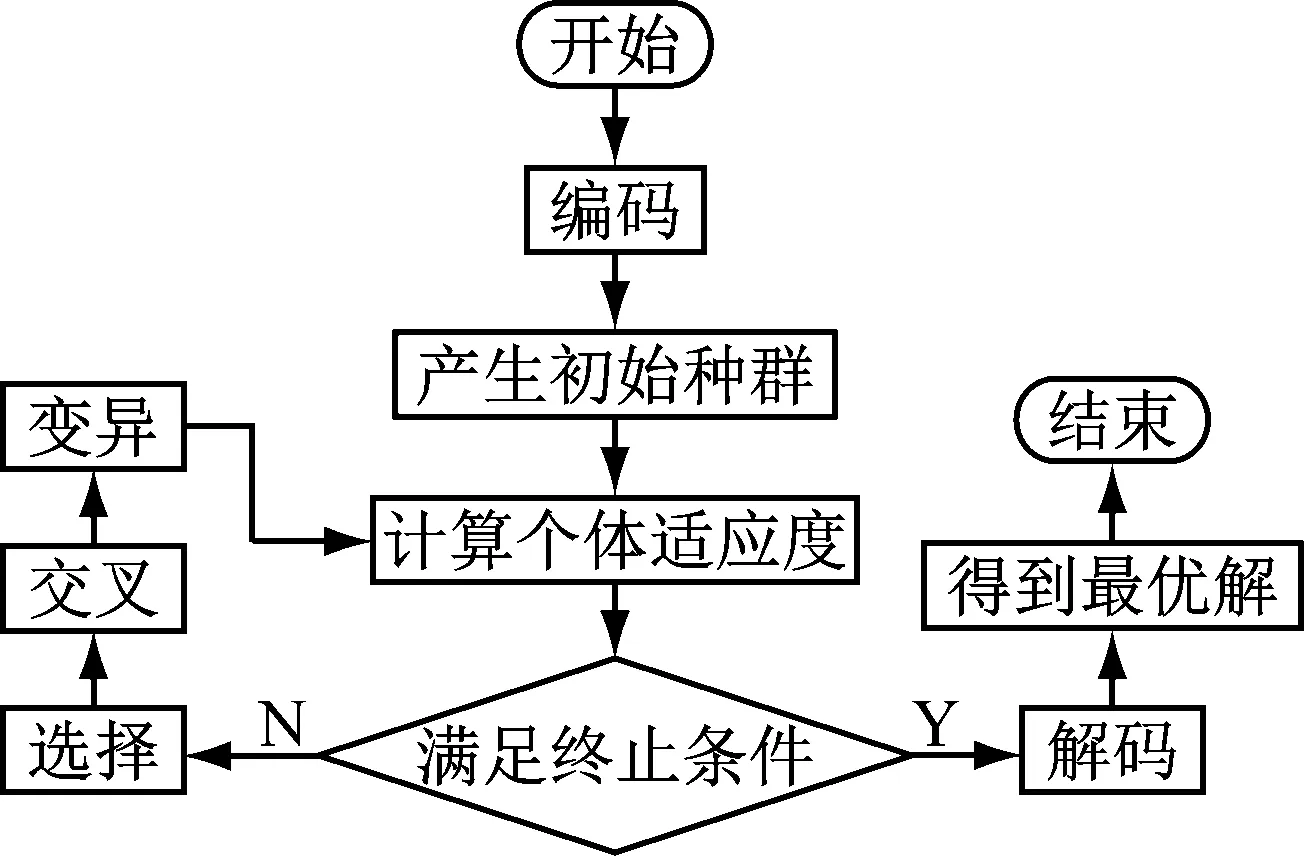
图3 遗传算法优化过程

1.4 GA-BP神经网络载荷识别过程

GA-BP神经网络主要由BP神经网络和遗传算法(GA)组成，用GA优化BP神经网络克服了BP神经网络易陷于局部最优和收敛速度慢等缺点，而且输出稳定性得到提高[21]。

根据1.1节～1.3节建立GA-BP神经网络模型，利用振动信号间接识别应力载荷过程如图4所示。

图4 载荷识别流程图

BP神经网络与遗传算法(GA)主要参数的设置，如表1所示。

表1 BP神经网络与遗传算法参数

1.5 误差评价指标

本文采用相对误差法来评估识别的应力载荷与期望应力载荷之间的误差，式(13)为相对误差法(RE)的计算公式[22]。

(13)

式中：p0为期望应力载荷；pi为识别的应力载荷；n2为2范数。

2 履带行驶系统试验

2.1 测试系统设置

通过振动信号识别应力载荷的试验对象为小型履带行驶装置(小车)，如图5(a)所示。采用外路测试法，通过遥控器远程操控小车前进后退。应用DH5902N坚固型动态信号测试分析系统进行振动加速度实时采集，应用DH5905N无线采集模块进行应力载荷的实时采集，试验采集到的振动加速度和应力载荷数据通过无线传输到计算机。应用DH5905N转速测量模块进行转速的采集，采集到的转速数据通过USB传输到计算机。

加速度传感器布置见图5(a)，在车体内部安装5个加速度传感器，采用平面磁力座固定，其中：#1、#2为1A111E型；#3为1A113E型，#4、#5为1A314E型；#1～#3加速度传感器布置于靠近支重轮处，#4、#5布置于靠近减速器-电机处。规定前进方向为+X，水平向右为+Y，垂直地面向上为+Z，加速度传感器主要测量垂直方向的振动。

DH5904型光电转速传感器与DH5905 N无线采集模块的固定方式，如图5(b)所示。图5(b)中辅助圆板为聚甲基丙烯酸甲酯材质的亚克力板，直径85 mm，厚3 mm，采用4个全牙内六角螺栓与驱动轮固定，轮缘缠绕531-1915M型号的黑色绒布胶带，用于粘贴反光条。辅助圆板还用于固定DH5905N的采集模块和电源模块。本文设计了一个十字形的固定架，配合转速传感器专用固定装置，可以实现转速传感器在X、Y、Z3个方向移动，以便于转速传感器准确固定。

应变片布置方式如图5(c)所示。在驱动轮靠近齿根处采用半桥贴片法固定两片BE120-3AA应变片，用于测量链板对驱动轮轮齿的作用力，从而近似得到链板间的拉力。图5(c)中Rg1和Rg2为应变片，应变片的4根引线分别焊接于对应的接线端子上，通过接线端子直接与DH5905 N连接。

(a) 加速度传感器布置

2.2 测试数据获取

测试之前，操控履带小车短距离往复运行3次，对小车运动状态及信号无线采集和接收系统进行检查，确认系统运行正常后，操控小车在硬质平路上直线行驶，行驶距离为8 m，行驶时间为12.35 s，反复测试6次相同工况数据。测试采样频率500 Hz，试验原始数据如图6所示。

从图6(a)～图6(e)可以看出，#1～#3振动加速度大部分在±2g波动，#4振动加速度大部分在±4g波动，#5振动加速度大部分在±3g波动。#5振动幅值大于#1～#3，这是因为#5传感器布置在左侧减速器-电机附近，有减速器-电机的噪音存在。#4振动幅值大于#5，因为#4传感器布置于右侧减速器-电机附近，且右驱动轮侧固定有转速传感器、DH5905N等装置，在小车运行过程中都会产生振动。

图6(f)中，应力载荷p主要分布在-3～8 kPa内。在0.5 s附近应力载荷幅值最大为10.81 kPa，因为0.5 s时小车处于从静止状态到运动状态的临界，电机启动力矩大于正常运行力矩。应力载荷曲线存在周期性变化，是由粘贴应变片处的轮齿与履带链板从啮合到脱离啮合一直循环运动引起的。图6(g)中，转速从0.8 s开始逐渐增大，小车的运动由遥控器控制，当运行平稳后，转速在180～210 r/min波动，平均转速为195 r/min。

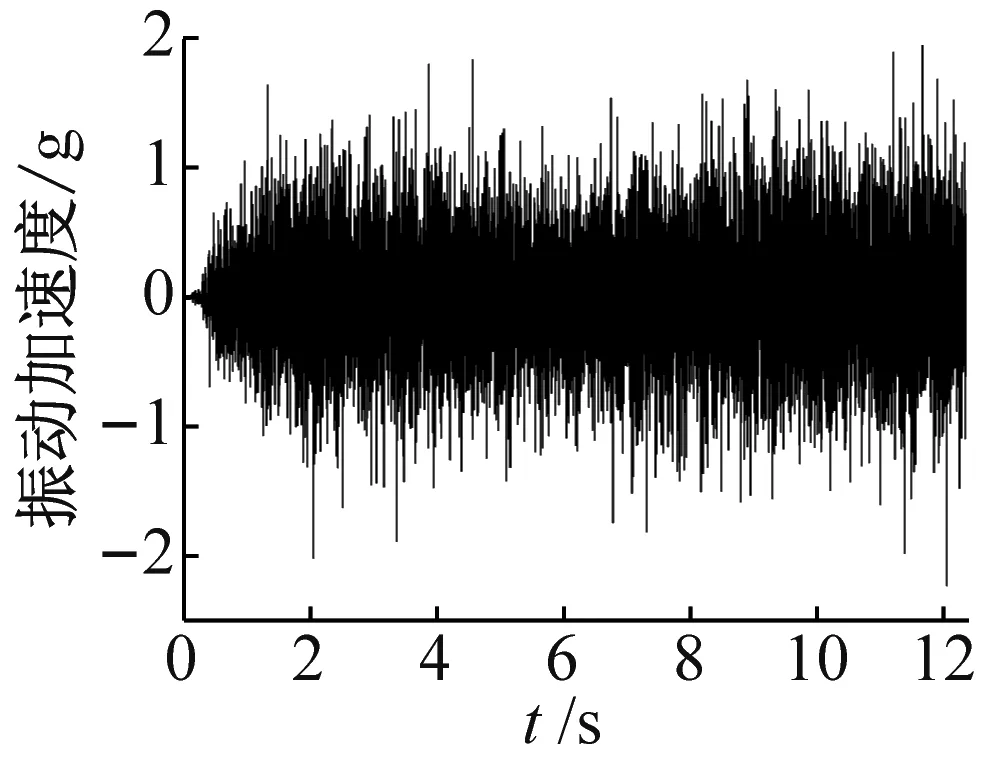
(a) #1振动加速度

2.3 数据预处理

试验测试的履带小车转速为195 r/min，驱动轮齿数为21，可计算得到驱动轮的转频fn为3.25 Hz，驱动轮与履带啮合频率fm为68.25 Hz。小车运行的路面由500 mm×500 mm的地板铺成，相邻地板间都有沟坑存在。每经过一个宽约20 mm的沟坑，10个支重轮都会与其产生冲击振动，试验时共经过17个沟坑。可计算得到路面不平度引起的振动频率fs=17×10/12.35，约为13.765 Hz[23]。

对试验测的应力载荷p和振动加速度进行快速傅里叶变换(fast Fourier transform,FFT)，得到数据的频谱图，如图7所示。

由图7(a)可知：#1～#5振动加速度的峰值13.68 Hz、69.47 Hz、137.90 Hz、208.00 Hz对应于路面不平度频率fs的1倍、5倍、10倍、15倍频，69.47 Hz、137.90 Hz、208.00 Hz对应于驱动轮啮频fm的1倍、2倍、3倍频，6.70 Hz、13.68 Hz、137.90 Hz、208.00 Hz靠近驱动轮转频fn的2倍、4倍、42倍、64倍频。

由图7(b)可知：应力载荷频率峰值3.24 Hz、6.56 Hz、9.80 Hz、13.00 Hz、16.36 Hz对应于驱动轮转频fn的1倍、2倍、3倍、4倍、5倍频，16.36 Hz、27.94 Hz、41.13 Hz靠近路面不平度频率fs的1倍、2倍、3倍频。

(a) 振动加速度频谱图

以上分析表明，履带车振动加速度和应力载荷的频谱峰值对应的频率多为路面不平度频率fs、驱动轮啮频fm、转频fn的整数倍频，因此路面不平度、驱动轮转动、驱动轮与履带的啮合为引起小车振动的主要因素。

从图7(b)可以看出原始应力载荷数据中含有大量高频噪声，需要对原始应力载荷进行去噪处理。对履带车振动和应力载荷影响较大的路面不平度频率fs、驱动轮啮频fm、驱动轮转频fn都在80 Hz之内，因此通过基于快速傅里叶变换的滤波器(FFT Filters)滤去80 Hz以上的噪音。去噪后的应力载荷如图8所示，应力载荷p主要分布在-2～7 kPa内，在0.5 s附近应力载荷幅值最大为10.1 kPa。

图8 去噪后的应力载荷

机体振动的频率是表示行驶平顺性的重要指标，履带式行驶系统的悬挂是根据驾驶员生理舒适性来设计的[24]。机体和弹簧振动的频率通过式(14)来估算

(14)

式中：f为车体和弹簧振动的频率，Hz；c为弹簧刚度，kN/mm；G1为机体作用在弹簧上的静载荷，kN；δi为弹簧在G1作用下的变形，mm；g为重力加速度，mm/s2。

履带小车加速度传感器的布置位置是在支重轮附近，支重轮与车体之间由弹簧悬挂连接。弹簧的变形量δi可以通过试验测得，根据式(14)可以计算得到机体与弹簧振动的频率f，结果如表2所示，表2中1号～10号为弹簧的编号。

表2 弹簧变形δi和机体弹簧振动频率f

从表2可以看出车体与弹簧的振动频率f都在10 Hz内，因此本文根据履带小车行驶平顺性指标选择频率在10 Hz内的振动加速度信号作为载荷识别的输入。

2.4 基于小波变换的振动特征提取

试验采集的原始振动加速度信号直接用于遗传神经网络进行载荷识别时，误差非常大，因此需要对原始信号进行处理。小波变换对信号的特征在时、频两域都有很好的表征能力，适用于本文的研究。

基于离散小波变换对原始信号进行j层小波分解，将原始信号看作第0层小波信号c0(n)，得到第j层分解后的低频分量cj(n)和高频分量dj(n)分别为

(15)

(16)

式中：h(k-2n)为低通滤波器；g(k-2n)为高通滤波器；n为采样点个数。

根据小波分解原理对信号进行小波分解，每一层子频带是由高频向低频对信号频率空间逐次进行二分的结果。原始信号频率空间V0=[0，fc]，第j层小波分解的低频和高频频率空间分别为[25]

Cj=[0,2-jfc]

(17)

Dj=[2-jfc,2-j+1fc]

(18)

式中：Cj为低频频率空间；Dj为高频频率空间；fc为采样频率。

小波变换中小波函数的选择十分重要，小波函数支集太长会产生边界问题，支集太短不利于信号能量的集中，sym8小波函数重构低通滤波器效果更好[26]。本文选择sym8小波基函数对振动加速度进行低频信号的提取。由式(17)可知，当小波分解层数达到5层时，小波分解的低频频率空间为C5=[0，15.625 Hz]，可以提取到10 Hz以内的振动加速度低频信号，小波5层分解后的振动加速度信号如图9所示。

由图9可知，经过5层小波变换提取的低频振动信号，在时域下的特征信息凸显了出来。硬质路面有沟坑存在，小车在接近匀速的情况下经过时，振幅峰值随着时间而接近周期性的出现。#3～#5测点在0.3 s附近有较大的峰值存在，分别为0.077g、0.089g、0.088g，约为运行平稳时峰值的两倍，这是小车启动时振动较大引起的。

(a) #1小波分解加速度

3 履带行驶系统载荷识别

GA-BP神经网络作为振动信号间接识别应力载荷的一种方法，其最佳隐含层神经元数(隐节点数)m的确定没有统一而完整的理论指导，一般只能通过经验选择[27]。隐节点数太少，BP网络不能充分学习样本规律；隐节点数太多，网络会把一些非规律内容也作为学习的样本进行学习，从而出现过度吻合。为了得到最佳网络性能，本文通过大量试验，得到图10所示规律：隐节点数从40开始，载荷识别相对误差有明显下降趋势。隐节点数在50～70，误差一直处于波动状态。隐节点数从71开始，载荷识别相对误差有上升趋势。当隐节点数为63时，载荷识别的相对误差最小为4.5%。

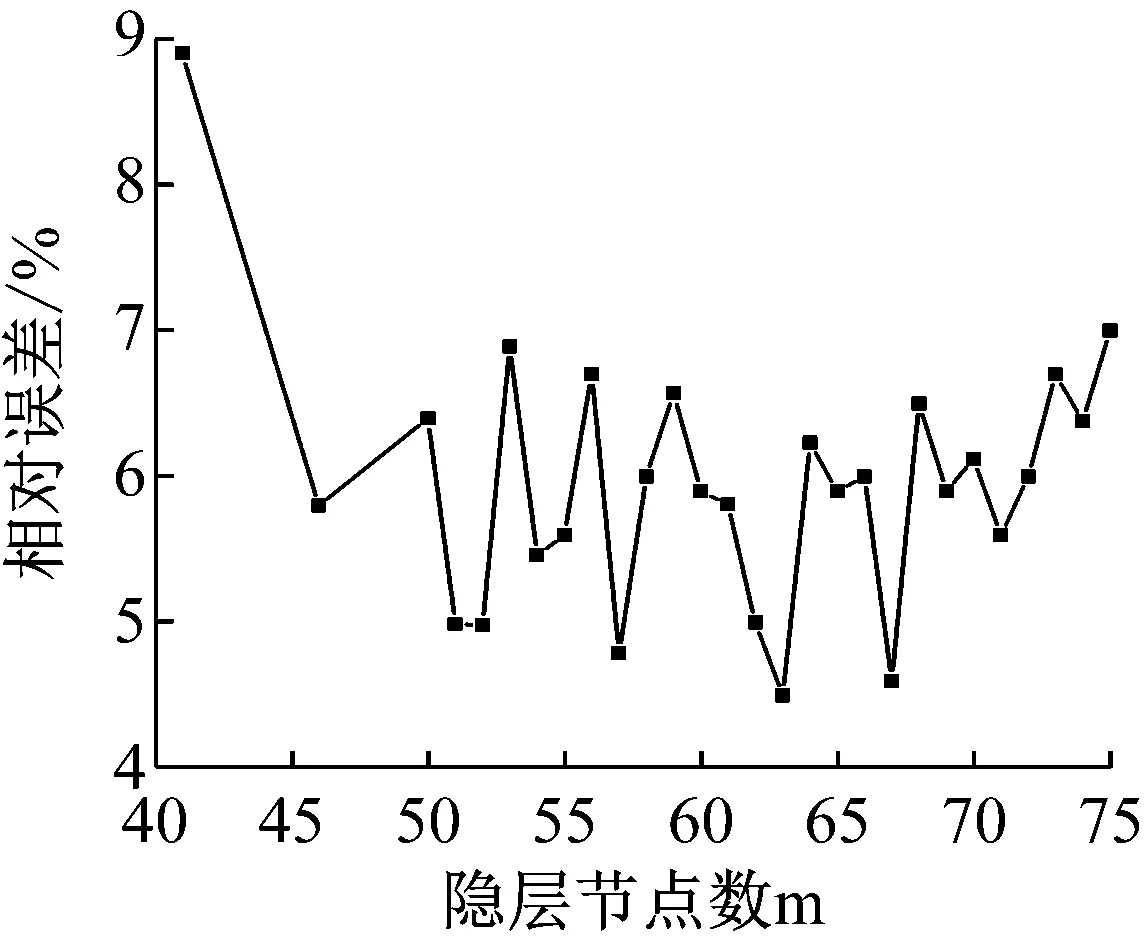
图10 隐含层节点数对GA-BP神经网络的影响

适应度函数根据BP网络的训练误差平方和倒数设计，作为遗传算法的评价准则。训练误差平方和越小，适应度就越大。本文得到的适应度曲线如图11所示。遗传算法设定遗传代数为100，随着遗传代数的增加，个体的平均适应度值是一直上升的，直到逼近最佳适应度。

图11 适应度曲线

试验采集的振动加速度和应力载荷信号通过频谱分析得到振动特征的主要频率成分，5组加速度信号经过小波5层分解后，每组信号选择1 000个数据点作为GA-BP神经网络的输入，基于FFT Filters滤波后得到的应力载荷信号选择1 000个数据点作为网络的输出，通过GA-BP神经网络的训练和学习，每组加速度信号选择150个数据点在训练好的网络中识别应力载荷，得到载荷识别的结果如图12所示，识别的应力载荷与滤波后的期望应力载荷非常接近，通过式(13)误差评价指标可以得到相对误差为4.5%。