滚珠丝杠垂直升降系统的建模和振动特性分析*
2022-02-22卢文婷陈嘉荣薛珺天
黄 晋 卢文婷 陈嘉荣 薛珺天
(①中国电子科技集团公司第二研究所,山西 太原030024;②太原师范学院物理系,山西 太原 030002)
滚珠丝杠副由于定位精度高,工作可靠,且可将伺服电动机的旋转运动转化为工作台的直线运动,因而作为机械传动部件广泛应用于各个领域的自动化设备中。其中的升降机构将滚珠丝杠副垂直安装,旋转运动转化为工作台的上下直线运动。目前,滚珠丝杠垂直升降系统没有明确的数学模型,系统的设计开发过程均依靠经验进行。但是由于伺服的激励,传动部件会产生振动,如果中间环节选型不合理,还会有共振的危险,严重影响滚珠丝杠副的使用寿命、噪声、温升、传动效率以及工作台的定位精度[1]。因此,建立滚珠丝杠垂直升降系统的数学模型并进行振动特性分析,指导系统设计过程和结构优化,对系统减振降噪和提升产品整体性能有重要意义。
已有众多国内外学者对滚珠丝杠传动系统进行了动力学建模与分析。向红标等人建立了某测量机Z轴滚珠丝杠进给系统的动力学模型[2],吴沁等人利用拉格朗日方程和能量原理建立了数控机床进给系统的数学模型,分析了各参数对工作台振动位移的影响[3], Frey S等分析了不同负载、工作台位置和丝杠螺距对进给系统混合模型和离散模型固有频率的影响[4],但是都存在模型简化程度大,没有考虑系统的初始条件等问题。集中参数模型能够估计滚珠丝杠进给驱动系统的轴向及扭转的低阶振动,但无法准确表征丝杆的柔性体特征[5-7]。Vicente D等人采用Ritz级数法表示丝杠轴向及扭转位移场的空间依赖性[8]。董亮等人将丝杠作为分布参数模型,其余部件作为集中参数模型,应用功率平衡法和Ritz级数法,建立了滚珠丝杠进给系统的振动模型[9],但是都没有对系统的动态响应进行分析。
针对以上问题,本文以某上下料自动化设备中的升降机构为研究对象,建立系统的动力学模型,仿真分析了系统的模态振型、固有频率以及动态响应。结果表明所建立的数学模型可以对滚珠丝杠垂直升降系统的选型设计和后期结构改进设计提供理论依据。
1 数学模型
1.1 拉格朗日方程
滚珠丝杠垂直升降系统的物理模型如图1所示,伺服电机通过联轴器带动丝杠转动,丝杠通过固定座安装在机架上,丝杠另一端利用深沟球轴承支持,这种固定-支持的安装方式能够抵消由热变形产生的应力,常被应用于精密滚珠丝杠驱动系统中[9]。
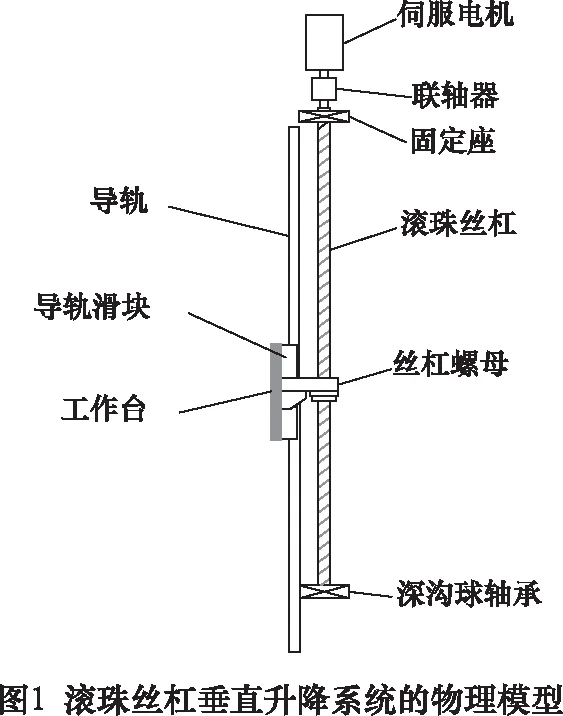
垂直升降系统的力学模型如图2所示。Jm为伺服电机转子转动惯量,忽略滚动轴承在扭转方向上的刚度和阻尼。Jc、Kc、Cc分别为联轴器的转动惯量、扭转刚度和扭转阻尼。Kb、Cb、Kn、Cn分别为固定座和丝杠螺母的轴向刚度和轴向阻尼。mt为负载质量,同时考虑负载总重量G2和负载与丝杠的总重量G1。E、ρ、A、G、I分别表示滚珠丝杠的杨氏模量、密度、横截面积、截切模量和极惯性矩。l表示丝杠的长度,γ表示丝杠的导程,κ表示丝杠的阻尼损耗因子。
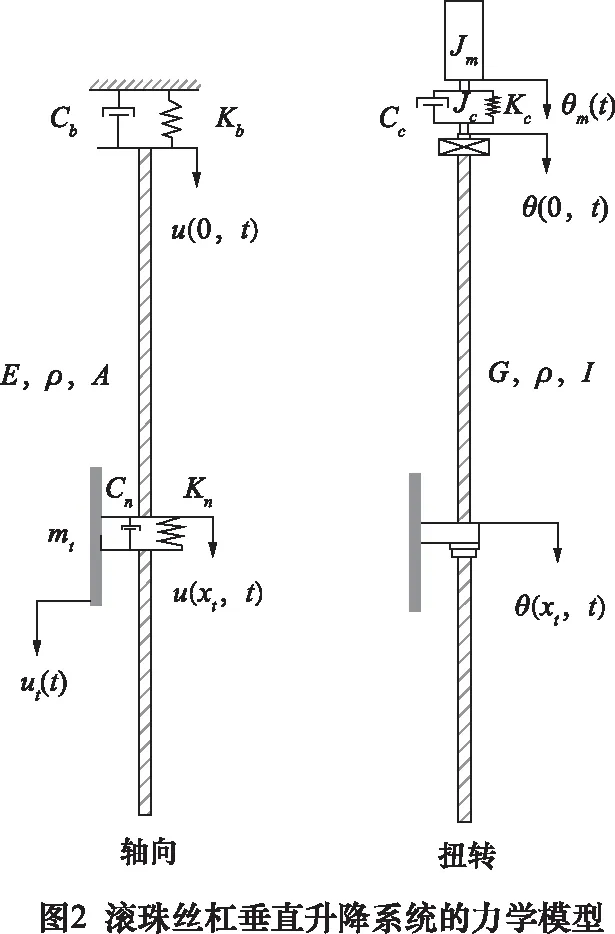
第一类拉格朗日方程为:
(1)
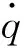
(2)
由图2可知,系统动能T包括工作台、电机转子、联轴器和丝杠的动能:
(3)
其中:“·”表示对时间t的导数;ut(t)表示工作台的位移;θm(t)表示电机转子的转角;u(x,t)和θ(x,t)分别表示丝杠的轴向位移函数和扭转位移函数;x是丝杠螺母的位移变量;xt是丝杠螺母的当前位置。丝杠螺母将丝杠的轴向和扭转振动耦合[10],螺母的轴向位移δn可以表示为:
(4)
系统势能V包括联轴器、丝杠螺母、固定座和丝杠变形的弹性势能:
(5)
由于系统存在阻尼损耗,则耗散能R可表示为:
(6)
丝杠作为连续体,可以用位移函数u(x,t) 和θ(x,t)来描述丝杠的变形,Ritz级数方法通过Ritz级数展开能够描述位移函数[10]:
(7)
(8)
其中φu(x)和φθ(x)是位移函数的基函数,系数qu(t)和qθ(t)表示基函数在某一瞬时的分量。基函数必须满足确定的条件以获得有效的Ritz级数展开,同时必须满足连续性、线性独立和几何边界条件[10]。基于以上分析,基函数可表示为:
φu(x)=cos(ju-1)πx/l
(9)
φθ(x)=cos(jθ-1)πx/l
(10)
其中:ju=1,2,…,Nu;jθ=1,2,…,Nθ。
取系统的广义坐标为θm(t)、ut(t)、qθ(t)、qu(t),则广义坐标矩阵表示如下:
(11)
将式(7)和(8)代入式(3)~(6)中,令:
得到系统的动能、势能和耗散能函数分别为:
(13)
(14)

(15)
由矩阵理论可推导出以下2个结论:
(1)设f=AX,其中f为标量,A为常量矩阵,X为未知矩阵,则有:
(16)
(2)设f=XTAX,其中f为标量,A为常量矩阵,X为未知矩阵,则有:
(17)
基于式(16)和式(17)的结论,将式(13)~(15)代入式(2)得到系统的质量矩阵、阻尼矩阵、刚度矩阵和广义激振力矩阵如下:
(18)
(19)
(20)
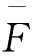
(21)


(22)
1.2 固有特性分析
无阻尼系统的特征方程为:
(23)

1.3 动态响应计算
由于模态叠加法相比于其他动力学分析方法具有高效、计算速度快的优点,动态响应分析采用了模态叠加法,通过在模态分析中获得的固有频率与振型来描述结构的动态响应。

将物理坐标q转换为模态坐标qp:
q=Apqp
(24)

(25)
令:
(26)
得到坐标变换后的系统动力学方程:
(27)
其中:质量矩阵Mp为对角矩阵;阻尼矩阵Cp不是对角矩阵,可通过降阶法求解系统微分方程,得到qp后代入式(24)可得到系统广义坐标q的时变特性。
2 案例仿真分析
以某上下料自动化设备中的升降机构为研究对象,对滚珠丝杠垂直升降系统进行模态分析和动力学分析,升降机构的三维模型和工程现场应用如图3所示。伺服电机和丝杠使用标准品,其他结构为自行设计。相关参数从产品目录和说明书中获取,具体参数见表1。
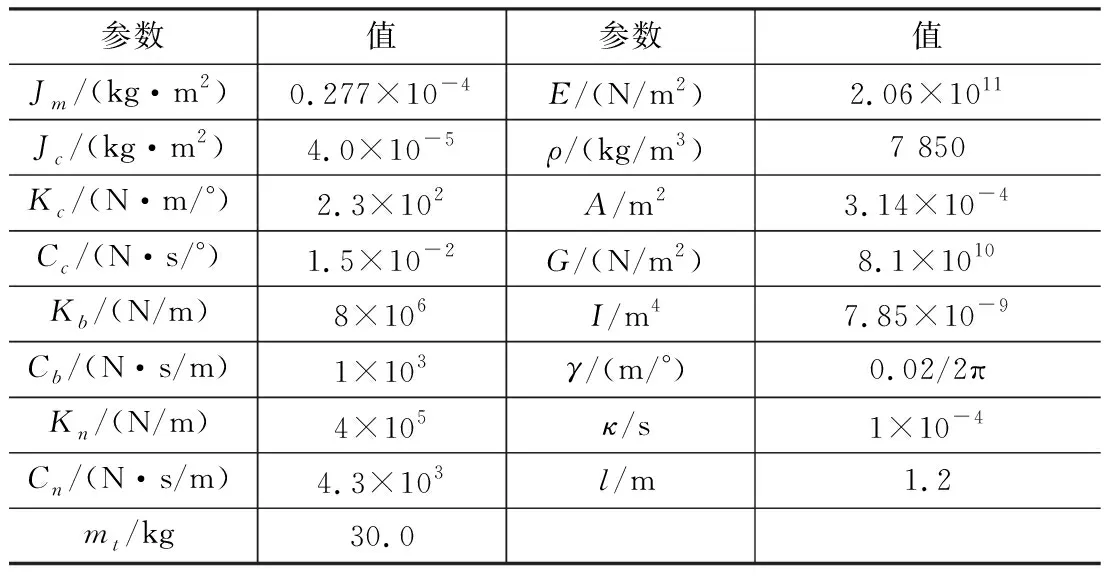
表1 系统主要参数

2.1 模态分析
将相关参数代入式(23),求解(23)式可得系统的固有频率和模态振型,表2列出了xt在0.5 m处时,Ritz级数长度Nu和Nθ取不同值时第一阶固有频率的数值仿真结果:

表2 固有频率随级数长度的变化
由于基函数的个数是任意的,且通过多个基函数的叠加,可以得到基频的近似值[11],由表2可知Nu和Nθ取不同值时基频不变,所以取Nu=Nθ=2进行系统的模态分析。
表3为工作台在不同位置下,系统第一阶到第三阶的固有频率。固有频率随工作台位置和负载质量的连续变化趋势如图4所示,第一阶固有频率受负载质量影响较大,负载质量越大,系统第一阶固有频率越小。机械系统的第一阶固有频率是决定系统频率响应带宽的的一个重要约束因素,在设计一个伺服控制系统时,通常要求机械系统的第一阶固有频率是系统带宽的5倍以上。图4和表3表明可以通过选择不同的结构参数获得合理的系统固有频率,预防共振的发生。

表3 固有频率随工作台位置的变化
表4列出了丝杠导程和螺母刚度对系统前三阶固有频率的影响,可以看出,在无预压的条件下,第一阶和第三阶固有频率随导程的增大而增大,而第二阶固有频率是和丝杠螺母的刚度成正相关。导程不变,增加预压,固有频率也增大,并且第一阶固有频率受影响较大。结果表明增大导程,增加预压可以提高机械系统的第一阶固有频率,增大传动系统的刚度和传动精度。

表4 固有频率随丝杠导程的变化
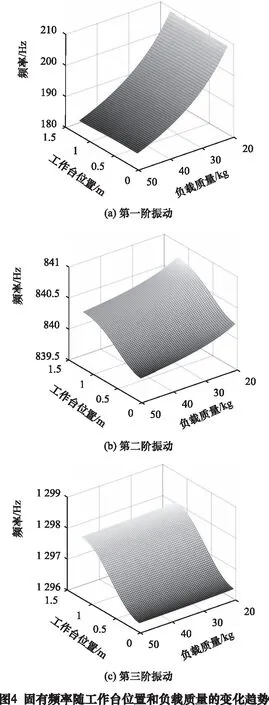

图5为丝杠的轴向振型曲线,图6为丝杠的扭转振型曲线。由图可知系统第一阶和第三阶振动主要是扭转振动,伴随较小的轴向振动,第二阶振动是丝杠的轴向和扭转耦合振动。由第一阶和第二阶扭转振型可知工作台越是远离电机端,丝杠的扭转振动越大。
由第一阶轴向振型可知工作台越是远离电机端,丝杠轴向振动越大。
从振型曲线可以知道某个自然共振频率下结构的变形趋势,若要加强结构的刚性,可以从这些较弱的部分加强。图5和图6表明最低频的模态主要是工作台在远离电机端的位置时丝杠的扭转方向,这是系统的薄弱位置,那么在后续升降系统的设计中应该将这一薄弱环节对传动系统的性能影响考虑其中。

2.2 动态响应分析
根据式(24)和式(27)编制MATLAB仿真程序,仿真时间100 ms,步长2 ms,得到工作台的位移响应以及各参数的影响。
滚珠丝杠和丝杠螺母结合处的轴向刚度和滚珠丝杠的预压等级有关,过大的预压力将造成摩擦扭矩增大及温升效应,寿命减短,但太低的预压力会使得滚珠丝杠刚性不足及增加失步的可能性。查阅滚珠丝杠技术资料可知,轴径为20 mm的滚珠丝杠,在无预压的情况下,导程为10 mm时刚性最大,5 mm导程次之,20 mm导程的刚性最小。
图7中,设定丝杠的导程为20 mm,增加丝杠螺母的预压,丝杠螺母轴向刚度增大,工作台的振动幅度减小,恢复平衡位置的时间从0.08 s减小到0.02 s。图8中,设定丝杠导程为10 mm,且无预压,5 mm和20 mm导程时增加预压使刚度相同,且20 mm导程时需要增加更大的预压,图8说明增加更大的预压后工作台的振动幅度更小。图7中实线为20 mm导程且无预压,图8中虚线为10 mm导程且无预压,比较可知20 mm导程时的工作台振幅更大且恢复平衡时间由0.06 s增大到0.1 s。图7和图8比较说明无预压状态下,丝杠导程越大,负载振幅越大,恢复平衡时间也越长。

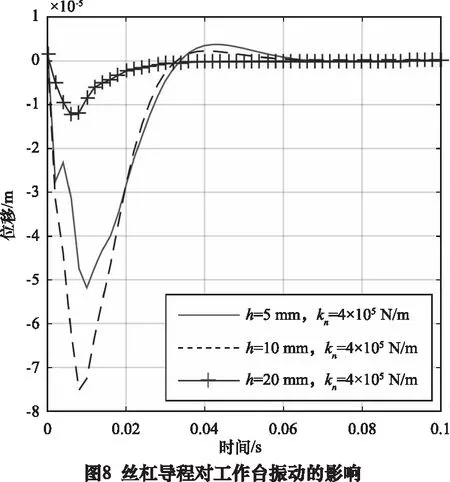
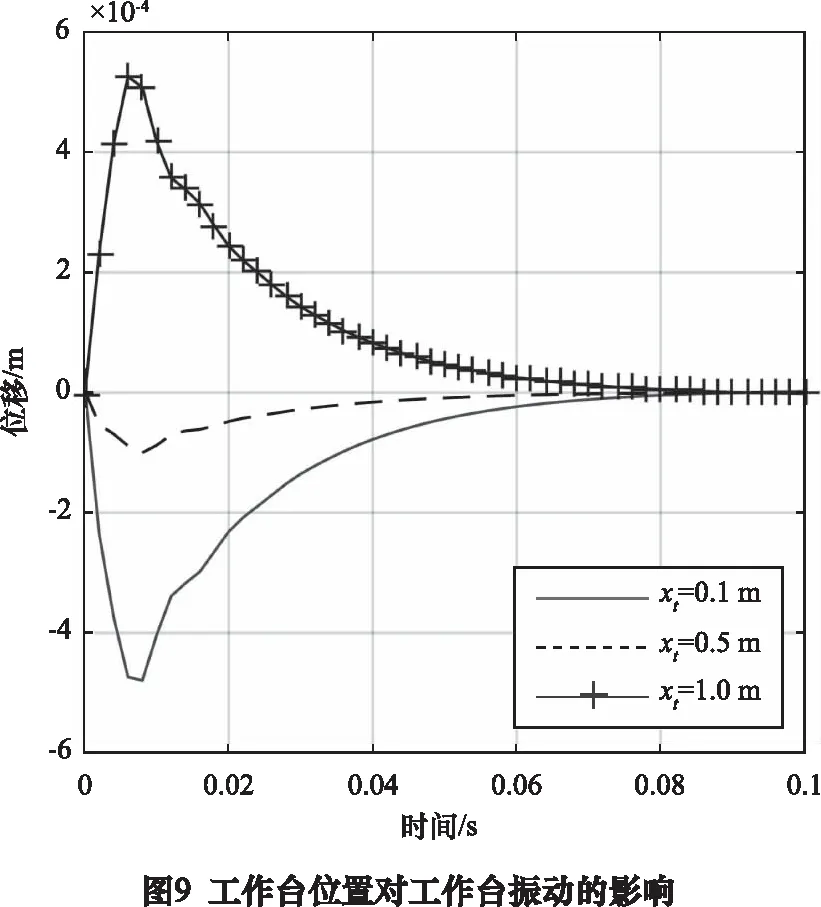

图9说明工作台位于丝杠中间位置的时候振动幅度最小,位于丝杠两端时的振动幅度较大。图10说明工作台质量增大会使得振动幅度增大,但影响较小。图7~图10说明工作台振动幅值随丝杠螺母轴向刚度的增大而减小,随丝杠导程的增大而增大。
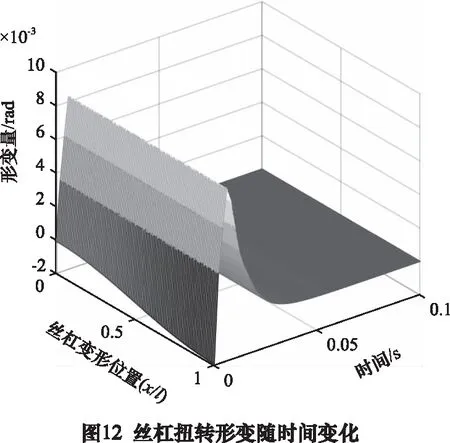
图11和图12显示了工作台位于丝杠中间位置时,丝杠的轴向和扭转振动情况,图11说明在丝杠轴向的振动两端较大,中间较小,图12说明丝杠的扭转振动是靠近电机端振动较小,远离电机的位置振动幅度变大。丝杠轴向振动比扭转振动更快的恢复到平衡位置。
工作台的振动会影响传动系统的定位精度,降低丝杠螺母副的使用寿命,因此,在设计过程中需要充分考虑系统的动态响应。
根据仿真结果,在设计升降机构时,同时考虑成本和需求,滚珠丝杠选择20 mm直径,10 mm导程,轴方向间隙预压等级选择P2,无间隙,轻预压,选型设计后的升降机构实际运行较之前更加平稳。

3 结语
本文研究了伺服激励下滚珠丝杠垂直升降系统的动态响应和影响因素,首先利用拉格朗日方法建立了系统的动力学方程,然后对系统进行了模态分析,最后通过模态叠加原理分析了不同参数对工作台位移响应的影响。主要结论有:
(1)固有频率随导程和丝杠螺母轴向刚度的增大而增大,负载质量对第一阶谐振模态有一定影响。
(2)系统模态振型分布表明第一阶和第三阶振动主要是丝杠的扭转振动,第二阶振动是丝杠的轴向振动和扭转振动的耦合。
(3)由位移响应分析可知工作台振动幅值随丝杠螺母轴向刚度的增大而减小,随丝杠导程的增大而增大。
