基于KALMAN滤波和深度学习的机器人飞拍方法研究*

田志彬 谢小辉

(苏州大学机电工程学院， 江苏 苏州 215100)

机器视觉取代人眼对环境进行感知，通过对目标工件形状、姿态及位置识别与定位目标，使工业生产线更加灵活、智能，解决传统工业离不开人工检测的问题[1]。在工业生产中，效率是一个重要的评价指标，飞拍定位是在动态过程中解决纠偏问题的方法，可以显著提高效率，所以飞拍在工业上的应用具有良好的发展前景。咸浩等人[2]基于机器视觉设计圆角袋单切系统，采用飞拍模式的视觉系统图像处理速度快，有效解决传统生产圆角袋时出现的效率低、废料多、机械磨损快等问题。黎扬进等人[3]提出一种卡尔曼—粒子滤波算法，有效提高了焊缝的跟踪精度。在移动对象轨迹预测高精度要求的应用领域中，基于轨迹拟合的传统预测算法已无法精准地预测出运动行为动态变化的移动对象的轨迹位置[4]。

本文拟针对对动态抓取的工件进行飞拍定位纠偏的场景，设计了视控一体化系统，改进卡尔曼滤波精准预测相机触发时机器人位置，设计ResNet50为基本框架的神经网络实现快速的图像处理，最终实现高精度、高效率的飞拍定位。

1 视觉-控制一体化实时系统搭建

传统的基于视觉的机器人控制系统，视觉与控制模块分离大都采用分离方案，相互之间通过TCP/IP协议实现数据通讯，实时性差；并且控制柜占用较大空间，视觉系统不轻便。结合现有机器人基于视觉的控制系统的不足，设计一种实时性、硬件系统简捷的视觉控制一体化系统，系统组成如图1。

在嵌入式工控机Windows系统上植入Codesys RTE，使工控机变为实时的控制系统，控制机器人的运动。同时在工控机上设计视觉系统，通过共享内存的快速交互方式获取机器人实时信息。通过Ethercat的通讯方式实现对机器人的运动控制，在一个通讯周期过程中，从站对数据帧的处理完全由硬件实现，所以延时很短，约为100～500 ns，这极大程度上保证了实时性。系统可以实现对物件的动态抓取以及飞拍定位。

2 算法的设计与分析

2.1 改进卡尔曼算法原理

植入Codesys RTE的实时系统实现机器人的运动控制，每隔Tms读取机器人的位置，并将位置信息通过共享内存的通讯方式传送到视觉控制端。由于时间间隔满足不了位置触发精度，所以通过改进卡尔曼预测算法精准预测下一个Tms时间点的位置，提前锁定触发位置所在的时间段，通过实时更新的运动方程对时间段进行分割，得到触发位置的时间点。通过C++库chrono实现对程序段的微秒级高精度计时和高精度延时，从而实现精准触发。卡尔曼算法示意图如图2。

卡尔曼滤波[5]是一种利用线性系统状态方程，通过系统的输入输出观测数据，对系统状态进行最优估计的算法。将卡尔曼滤波算法应用于移动对象动态轨迹预测具有实时性高的优势，对频繁变换运动状态的移动对象具有较高的自适应性，是一种普适的机器学习方法[6]。

卡尔曼滤波动态轨迹预测系统的状态方程和观测方程，如下所示:

系统的状态方程(预测方程)：

xk=Ak×xk-1+Bk×uk+wk

(1)

观测方程：

zk=Hk×xk+vk

(2)

式中：xk是状态向量；Ak是状态转移矩阵；Bk是控制变量的矩阵；uk是状态控制向量。

由于传统的卡尔曼预测应用此场景时有较大位置预测误差，所以对传统的卡尔曼滤波进行改进。前几次迭代中还是应用传统的时间更新公式：

(3)

(4)

误差稳定之后，引入反馈向量sss=[ss0]，ss为前一时刻先验估计位置预测误差。

(5)

(6)

对于变加速运动，在测量更新中实时更新每段间隔的加速度，利用上一时间段的加速度，更新下一时间段的位移和速度。观测更新方程如下：

(7)

(8)

(9)

前几次迭代中，引入较小的加速度，稳定位置和速度：

(10)

误差稳定并且引入反馈向量sss之后，更换加速度更新方程：

(11)

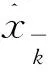
2.2 基于ResNet50网络的深度学习网络原理

深度学习目标检测算法可以从功能上分为两部分，其一是提取语义信息的骨架特征提取网络，其二是对提取到的语义信息进行运算、得出最终结果的结果预测网络。为了提高模型目标检测的准确性，考虑选择合适的骨架网络和预测网络进行合理组合与优化，并且建立合适的损失函数，结合动量法优化网络。图3为改进的网络结构模型。

(1)部分是ResNet50骨架网络，ResNet50是具有残差结构的神经网络。在解决梯度的过程中往往伴随深度加深[7]，该网络能有效防止在反向传播过程中梯度弥散问题[8]，进而解决梯度变化时深度加深问题[9]。(2)部分是特征金字塔网络，它是一种多尺度特征融合网络，通过特征金字塔网络融合高层特征和底层特征的优点，进行更准确的检测。(3)部分对特征图进行学习，通过优化函数调整过程参数较小损失函数值，对潜在目标进行定位和分类，通过置信度分析减少重叠的预测边界框。

为了解决Hessian矩阵病态条件问题，引入动量优化算法，它能够引导迭代方向朝着正确的方向进行。如果前一刻的梯度与当前的梯度方向差别很大，不加处理的话该时刻会有大幅徘徊的梯度。由于动量积攒了历史的梯度，把历史梯度叠加到当前时刻梯度上，从而使得当前时刻的梯度幅度减小。

更新公式：

vt=γ×vt-1+α∇

(12)

θnew=θ-vt

(13)

公式(12)为动量更新公式,vt-1为之前所有步骤所累积的动量和，γ为动量参数，α为学习率，∇为梯度，θ为待更新参数。

2.3 算法应用于飞拍的理论分析

脱离传感器触发的飞拍纠偏定位主要包括以下两个过程：

(1)示教：设定一个相机触发位置，通过改进的卡尔曼算法精准触发相机拍照，通过深度学习识别图像的ROI区域，对ROI区域图像进行边缘检测及相关处理，得到精确的图像位姿信息。最后示教机器人精确装配工件，记录机器人在装配的位姿信息。得到的图像和机器人位姿作为飞拍纠偏的模板信息。

(2)飞拍纠偏：确保在同一位置得到工件的图像坐标，通过深度学习快速识别图像的位姿信息，与模板信息进行偏差计算，得到的偏差就是工件的偏移信息。通过手眼标定，将工件的偏差转换到机器人坐标下。在机器人下一节拍前，将偏差叠加到模板信息中生成新的机器人目标位置，实现对工件的高精度装配。

3 实验分析

3.1 改进卡尔曼算法实验分析

卡尔曼滤波器的观测量可以少于动态系统中状态向量所包含的元素个数。所以测量向量只有一个位移变量，为一维向量。采样时间为4 ms,把每隔4 ms实时采集的机器人Y轴位置作为测量向量zk的主要部分，创建状态向量x=[sv]，Ak=[1,ΔT;0,1]，Bk=[ΔT2/2;ΔT]，Hk=[1,0],测量噪声为±0.000 5，测量噪声协方差R为0.000 5，过程噪声协方差Q=[0,0;0,1]。取第一个数据点为0时刻，从第9个点开始迭代，预测结果图见图4。

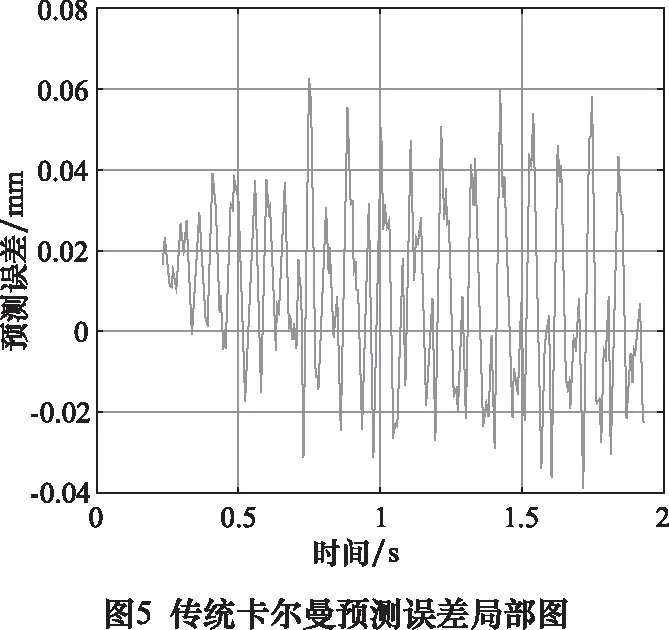
由图5可以看出，传统的卡尔曼预测误差达到稳定后波动较大，1.2 s后，最大误差值达到0.059 7 mm,标准差为0.024 5 mm。如图6，1.2 s以后，用上一时刻先验估计误差进行反馈，位置预测误差明显减小，误差基本位于±0.02 mm内,并且最大误差降低到0.037 6 mm,标准差为0.013 4 mm。与传统方法相比，预测精度得到了明显提高。

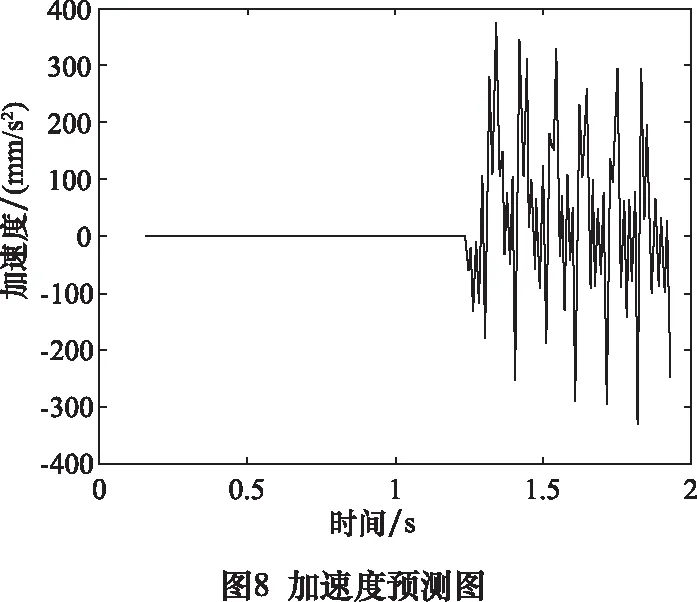
速度变化比较平稳，加速度虽然波动较大，但是加速度叠加在ΔT2=0.000 016上面，对于预测精度影响不大。因此前面可以利用较小的加速度稳定卡尔曼滤波的过程参数，后面更正加速度表达式，进行精准预测。

当改进的卡尔曼滤波算法预测到下一时间点的位置大于触发的位置时，算法停止迭代。利用上一时间点的速度和预测速度，对上一时间点和预测时间点的这一时间段进行分割，找到触发位置的时间点。由于时间段足够短，加速度对位移基本没有影响，分割过程可以按照机器人匀速运动处理。

时间段的分割公式：

(14)

利用chrono库中system_clock::now()函数，设计微秒级计时和延时程序，用于对预测算法进行耗时计算和延时触发。通过测试改进的卡尔曼滤波迭代一次的时间Tl不超过8 μs。所以精准延时时间为Te=T-Tl。

SCARA机器人空载，机器人运行最大速度设为150 mm/s,对改进的卡尔曼滤波进行精度验证。由于机器人末端固定，并且采用左手系运动，其末端的圆心位置与机器人空间位置一一对应，即验证每一帧图像的中心位置坐标差值即可。

通过改进的卡尔曼滤波触发相机采集图像，进行200次实验，机器人末端中心的Y轴图像坐标如图9所示。

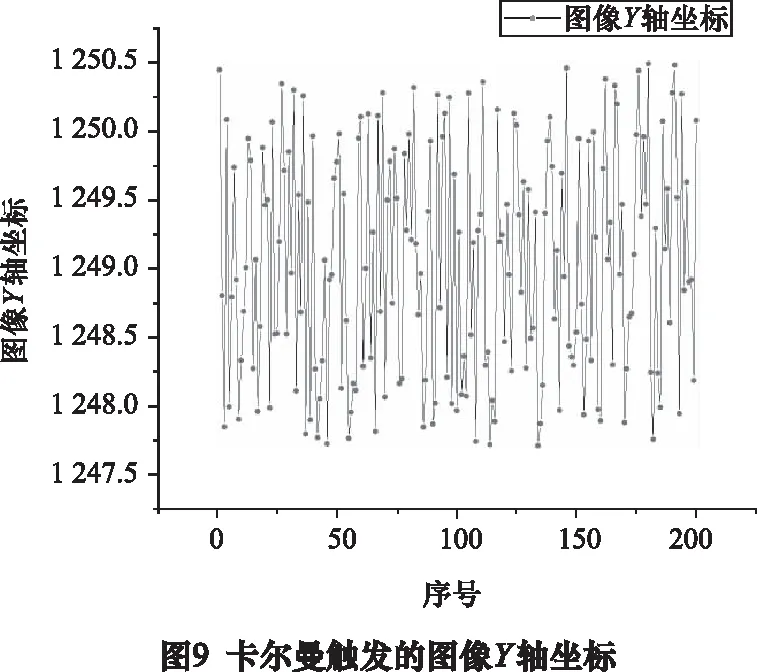
由上述实验数据得出，均方差为0.827 px,最大偏差为2.781 px。即均方差为0.017 378 mm,最大偏差为0.058 4 mm，触发重复度满足后续飞拍实验的要求。

3.2 深度学习网络训练实验分析

搭建网络后对1 500张工件进行训练，将70%作为训练集，15%作为验证集，15%作为测试集。最大训练步数设置为200，学习率参数为0.000 5，动量参数为0.9。准确率最终稳定在95%左右，损失函数小于0.05，生成best.hdl文件，后面调用训练好的网络文件即可获取训练框的大小和方向。基于GPU型号为GeForece GTX1050ti的应用识别时间在50 ms以内，基于CPU应用时间在90 ms以内。由于在线实验时工控机型号的限制，采用基于CPU的深度学习应用。图10为训练过程可视化图。

图10中，最上层为输入图像，中间层为标注图像，最下层为训练结果。

3.3 飞拍实验分析

实验采用海康工控机MV-VB2210-120G,驱动器为STEP四轴驱动器，相机分辨率为3 072 × 2 048，光源采用环形光源,SACRA大臂小臂长为200 mm。机器人位置(200,5.6,60)设为相机触发位置，实时获取机器人位置的周期设为4 ms。

按照前面所述的飞拍过程进行飞拍实验的结果：

(1)示教：在机器人位置(200,5.6,60)处触发的图像像素坐标为(1 702.38,1 351.79)，姿态为12.32°；示教得到的机器人装配时坐标为(200.52,202.73)，姿态为11.63°。

(2)飞拍纠偏：SCARA吸取芯片后，经过预测算法触发相机拍照，然后利用神经网络快速识别芯片的位姿，与步骤1得到的模板像素坐标进行偏差计算，然后将偏差值转换到机器人坐标下，进而叠加到步骤1中的机器人示教坐标上得到精准的目标装配位置。通过固定相机对放置结果进行误差测量，把x方向和y方向误差的平均值视为定位误差。

实验测试了机器人在不同速度下应用视控一体方法进行飞拍纠偏定位，每个速度下进行200次测试，实验结果及实验场景图如图11所示。

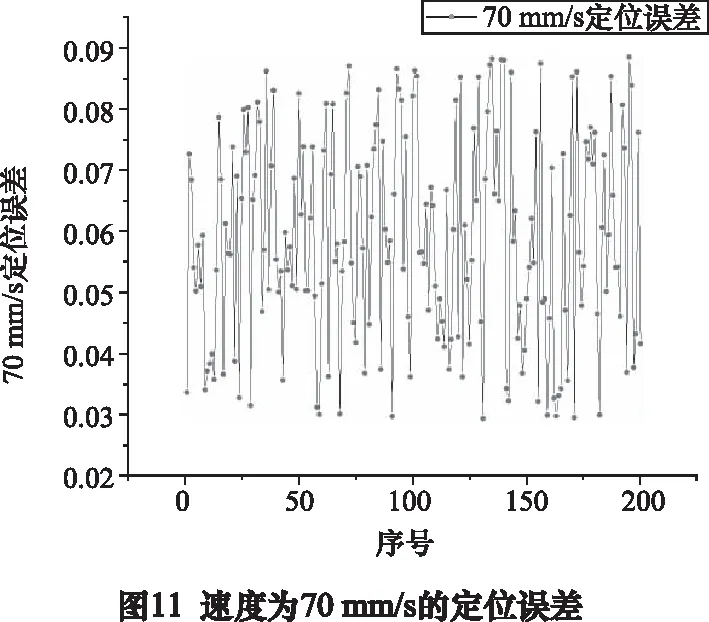
对图11～图14结果进行统计计算，计算结果如下表:

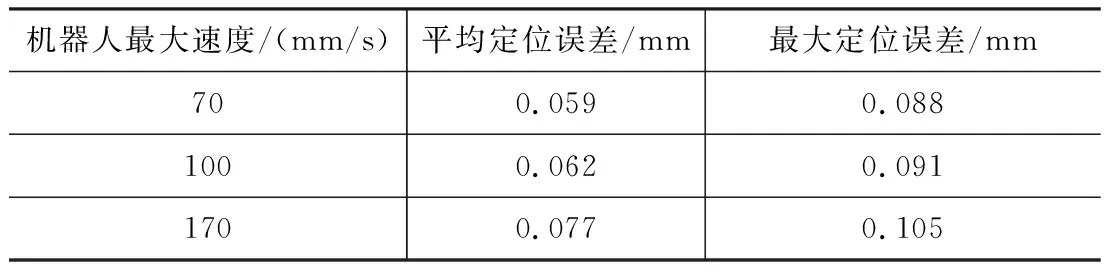
表1 实验结果

机器人最大速度为70 mm/s时，平均定位误差在±0.06 mm以内；最大速度为100 mm/s时，平均定位误差在±0.065 mm以内；最大速度为170 mm/s时，平均定位误差在±0.08 mm以内。并且最大定位误差均不超过±0.11 mm。

4 结语

通过本文的研究，采用视控一体化的机器人飞拍系统较之传统的视控分离方案，系统简捷易用，具有实时性高的特点。提出一种无传感器的精准时间触发算法，结合深度学习实现精准的飞拍定位。经过1 000次的飞拍实验测试及其数据，表明：通过采用深度学习算法，针对贴装芯片工件的飞拍实验，最快算法时间在50 ms以内，传统的模板检测时间为150 ms；通过采用改进型KALMAN滤波算法，较之传统的卡尔曼滤波算法，在应用此场景时，预测误差的标准差从0.024 5 mm提高到0.013 4 mm,最大预测误差从0.059 7 mm减小到0.037 6 mm；通过两者相结合，基于视控一体化系统，平均定位误差在0.08 mm以内，良率96%，系统成本大大降低。因此，本文提出的机器人视觉飞拍系统具有简捷易用、精度高和效率高优点，能够满足工业应用的需求。