横流对振荡射流冲击冷却特性影响的数值研究

汪 胜， 韩 东， 周天昊， 李世瑞， 何纬峰， 王瑾程

(南京航空航天大学 能源与动力学院，南京 210016)

冲击射流是一种具有很大潜力的强化换热方式。由于冲击射流具有较好的局部换热效果，其在先进燃气轮机高温部件冷却、电子设备冷却等方面都有重要的应用。冲击射流冷却根据射流的特性分为稳态冲击射流和非稳态冲击射流。稳态冲击射流的相关基础研究已有很多，然而在实际工程应用中，稳态射流仅在冲击点处有较好的对流换热效果。当采取阵列排布时，相邻射流会在近壁面处形成二次滞止区，显著降低靶面的换热效率[1-3]。1975年，Viets[4]设计了一种具有反馈回路的自激射流振荡器，该器件能够使稳态的入口气流转换成非稳态的振荡射流，且结构简单，不包含运动部件，具有较长的使用寿命。

近几年的研究表明，振荡射流在冲击换热领域相较于稳态射流有更好的换热性能[5-8]。Kim等[5]通过实验研究了射流振荡器冲击壁面的流场特性，并比较了相同条件下方孔射流冲击靶面的换热特性，结果表明振荡射流由于扫掠运动能够在近壁面处产生显著的湍流从而强化靶面换热。Wu 等[8]通过数值模拟研究了工质为水的振荡射流的冲击换热特性。但是这些研究大都集中在单个振荡射流冲击靶面的换热特性。在实际工程应用中，当若干射流振荡器阵列排布时，上游射流冲击靶面形成的横流势必会对下游射流产生较大影响[9]。目前，横流对振荡射流的影响机制尚不清楚，且大多数研究都集中在横流对外部流场流动状态的影响[10-11]，而关于横流对冲击冷却的影响研究较少。

此外，对于如何减少横流对冲击射流换热的削弱作用，许多学者提出改变靶面形状、在目标靶面上增加涡发生器等方法，然而这些方法都会造成额外的压降损失[12-14]。笔者对初始横流作用下的振荡射流冲击冷却进行了数值研究。在钢材的热处理或电气设备冷却等实际工况下，冲击射流入口速度一般为10～30 m/s，前排射流冲击靶面形成的横流堆积下横流速度为2～10 m/s。数值模型中冲击间距Z=2D(D=10 mm)，对横向排列和纵向排列下的射流冲击雷诺数分别为16 400、21 800，横流雷诺数为3 600～14 400的若干工况进行数值模拟，并通过流场分析对振荡射流冲击换热的机理进行研究。最后，通过修正排布角度来减小横流对振荡射流的偏转作用，从而增强横流影响下冲击核心区的换热效果。

1 研究对象

本文的射流振荡器模型由文献[3]中的模型等比例放大得来，其三维几何细节如图1所示。喷嘴入口宽度为2D，回流通道宽度为D,出口的喉部宽度为D，整体高度为0.5D。经过简化后的2种计算模型如图2和图3所示。振荡射流出口到靶面的距离即冲击间距Z=2D,冲击腔的高度为4D。图2中的横流方向与振荡射流振荡方向平行，排布方式为横向排列；图3中的横流方向与振荡射流的振荡方向垂直，排布方式为纵向排列。射流入口的气流经过射流振荡器产生振荡射流冲击靶面后，再随初始横流从右侧出口流出。在靶面上定义冲击核心区，其位置居于靶面中心且为2.7D×2.7D的正方形几何区域。

图1 射流振荡器几何模型

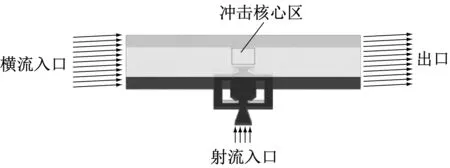
图2 横向排列模型

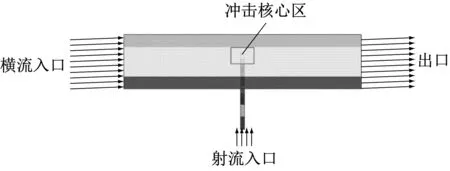
图3 纵向排列模型

为了模拟射流振荡器阵列布置下前排射流冲击靶面形成的横流对后排某位置的振荡射流冲击靶面换热的影响规律，射流入口及横流入口均为速度入口，出口设定为一个标准大气压的压力出口。靶面的热流密度设为恒定值10 000 W/m2，其余壁面设定为绝热且无滑移条件。

2 计算方法

2.1 计算模型及网格划分

该模型采用结构化的六面体网格。由于射流振荡器内部以及冲击靶面附近流动相对复杂，对射流振荡器内壁面及靶面附近的网格进行加密，使得其y+保持在1左右。为了减少网格数量对计算结果的影响，首先进行了网格无关性验证。采用的网格数量为60万～240万，计算结果如图4所示。由图4可以看出，180万网格数量时射流振荡器产生振荡射流的频率与240万网格数量时的振荡频率仅相差0.6%。为了节约计算资源，采用网格数量约为180万时进行计算，模型典型几何特征处的网格划分如图5所示。

图4 振荡频率随网格数量的变化曲线

(a) 射流流道处网格

(b) 冲击腔处网格

2.2 计算工况

采用商业软件CFX进行流体动力学分析，压力-速度耦合采用Simple算法，采用SSTk-ω湍流模型，通过壁面函数法不断调整壁面网格，使y+满足湍流模型的需要。所有物理量均采用二阶迎风格式进行离散，时间步长为10-3s。收敛标准为在每个时间步长内，质量方程和动量方程的残差小于10-3，k方程、ω方程及能量方程的残差小于10-6，且出口流量不随时间变化。

入口雷诺数Rej定义为：

(1)

横流雷诺数Rec定义为：

(2)

式中：uj为射流入口速度；uc为横流入口速度；Dj、Dc分别为入口喉部及横流入口的特征长度；ν为空气在293 K下的动力黏度。

2.3 模型验证

将相同入口雷诺数条件下靶面平均努塞尔数的模拟结果与文献[8]中的结果进行对比(见表2)，以验证本文模型的可靠性。通过计算可得，靶面平均努塞尔数模拟结果与文献结果的误差在6%～12%，表明所选模型和参数基本合理，能够较为准确地模拟不同入口雷诺数下振荡射流冲击换热的换热效果。

表1 平均努塞尔数模拟结果与文献结果的对比

3 结果及分析

3.1 射流振荡器内部流场分析

图6为射流振荡器的内部流场速度云图，以振荡射流垂直冲击的时刻作为一个振荡周期tf的起始时刻,t为时间。在振荡开始阶段，即t=0 s时，气流经射流振荡器入口进入混合腔。由于流体的附壁效应，气流会向混合腔的右侧偏转，并在出口附近壁面形成驻点，迫使一部分气流进入左侧的回流通道，其余的气流则由喷嘴喉部射出。当t=1/8tf时，进入回流通道的气流在入口处聚集，该处的压力升高，使得混合腔内气流开始向右侧偏转，外部流场的气流开始向左侧发生偏转。当t=1/4tf时，外部流场的气流向左侧达到最大偏转。当t=3/8tf时，进入右侧回流通道的气流开始逐渐增多并在入口处聚集，迫使入口射流开始向着远离中心轴线的方向偏转。当t=1/2tf时，混合腔内部的气流开始逐渐向左侧偏转，外部射流回到初始位置的中心轴线位置，振荡射流完成半个周期的振荡。在接下来的半个周期内气流开始向另外一侧偏转，其流体动力学模式与前半个周期完全对称。随着上述过程的重复出现，射流振荡器能够产生持续的振荡射流。笔者观测到的射流振荡器内部流场流动状态与文献[6]和文献[7]中的流动模式几乎相同。

3.2 横流作用下的振荡射流流场分析

由于出口射流在腔体内来回振荡，为了研究方便，流场分析的重点放在振荡射流冲击靶面的典型位置。图7分别为3个时刻下无初始横流横向排列、有初始横流横向排列、有初始横流纵向排列的中心轴截面上的流线图。由图7可以看出，在无初始横流的作用下，射流能够较好地冲击到靶面的中心区域，并在冲击点附近形成卷吸涡结构。而在有初始横流的条件下，射流的冲击点会向下游移动，且横流在遇到射流时会由于逆压力梯度在近壁面处形成马蹄涡，该马蹄涡在整个振荡周期内都存在。由图7还可以看出，在相同横流雷诺数条件下，纵向排列时近壁面处形成了更强的马蹄涡结构。

图6 振荡射流半个周期内各时间节点的速度云图

Fig.6 Velocity contour of each time node in an half cycle of the oscillating jet

3.3 横流作用下靶面换热分析

对2种排布方式下的射流振荡器在有初始横流的工况下冲击靶面的换热性能进行分析。由于射流振荡器在流体进入腔体内的初始时间内振荡不稳定，所以本文的换热结果均采用射流振荡器稳定振荡后10个振荡周期内冲击靶面换热的时均努塞尔数(以下简称努塞尔数)表示。其中努塞尔数Nu定义为：

(3)

其中，参考温度Tf为300 K；特征长度选取喉部的水力直径Dh,为6.67 mm；靶面的热流量q设定为10 000 W/m2；气流温度T取300 K；λ为空气在300 K下的导热系数。

3.3.1 横向排列下靶面换热分析

图8和图9分别为2种排布方式在不同入口雷诺数下靶面中心线上努塞尔数随初始横流速度变化的分布情况。由图8和图9可以看出，与无横流时相比，距离横流入口较近的位置努塞尔数明显减小。由前文的分析可知，射流冲击靶面会形成卷吸涡结构，该结构会强化主流与近壁面处流体的掺混作用，减小冲击位置的热边界层，因此卷吸涡可以有效强化该位置的传热。而横流造成冲击点位置向下游移动，距离横流入口较近的位置无法被射流冲击形成卷吸涡，从而削弱了该位置的传热效果。此外，这种冲击点移动的效果也会造成靶面高换热区域向下游偏移。

图7 射流振荡器中心轴截面上流线图

Fig.7 Streamlines on the central axis section of the jet oscillator

由图8还可以看出，横向排列下靶面中心线位置整体上努塞尔数随着横流雷诺数的增大呈现先减小后增大的趋势。这是因为射流穿过横流时，在横流强度较低的条件下(Rec=3 600)会阻碍射流冲击靶面，削弱振荡射流的强度，从而降低靶面的换热效果。而随着横流强度的增大(Rec=7 200)，逆压力梯度形成的马蹄涡在强化换热效果上占据主导地位，因此整体的努塞尔数越来越大。

(a) Rej=16 400

(b) Rej=21 800

(a) Rej=16 400

(b) Rej=21 800

图10为横向排列下靶面冲击核心区的平均努塞尔数(Num)分布。由图10可以看出，冲击核心区的平均努塞尔数随着横流雷诺数的增大而不断减小。当横流强度较小时(Rec=3 600)，横流会整体削弱振荡射流冲击靶面的强度从而削弱换热效果。随着横流强度的增大，高换热区域从靶面中心区域向下游移动的趋势越来越明显，这同样会削弱冲击核心区的换热效果，因此该区域的平均努塞尔数越来越小。

图10 横向排列下靶面冲击核心区平均努塞尔数分布

3.3.2 纵向排列下靶面换热分析

由图9还可以看出，纵向排列下初始横流对靶面中心线上高换热区域的偏移效果较弱，但是明显增大了高换热区域的努塞尔数。这是因为在这种排列方式下，初始横流的方向始终与振荡射流的振荡方向垂直，射流冲击靶面的冲击点位置受横流影响较小。而在较强的逆压力梯度下形成的马蹄涡作用下，该处的换热效果得到有效增强。

图11为纵向排列下靶面冲击核心区的平均努塞尔数分布。纵向排列下平均努塞尔数随着横流雷诺数的增大先增大，当横流雷诺数为7 200时达到峰值，随后逐渐减小。纵向排列下靶面高换热区域的换热在强烈的马蹄涡作用下会得到有效强化，在横流强度较小时(Rec=7 200)，这种效应较为突出。随着横流强度的进一步增大，高换热区域的后移逐渐占据主导地位，冲击核心区的换热效果越来越差。

图11 纵向排列下靶面冲击核心区平均努塞尔数分布

3.4 横流冲击修正模型

横流造成的冲击点后移会显著削弱冲击核心区的换热效果。为了减小这种影响，图12给出了射流振荡器倾斜排布情况，其中倾斜角度(即排布角度)分别设置为0°、5°、10°、15°、20°和30°。在纵向排列下入口雷诺数为21 800，横流雷诺数为14 400时，通过数值模拟研究了有初始横流工况下排布角度对振荡射流冲击靶面的换热效果。

图12 射流振荡器偏转布置模型

由图13可以看出，倾斜排布冲击下中心线上的波峰位置相对于垂直冲击向左侧移动。这是因为倾斜排布会造成冲击点整体向左移动，这在一定程度上可以弥补高换热区域后移对靶面换热的削弱效果。此外，当排布角度较小时虽然会导致换热努塞尔数峰值降低，但是随着射流振荡器排布角度的增大，高换热区域附近的马蹄涡结构也会得到强化，从而提升换热效果。

图13 各排列方式下中心线上的努塞尔数分布

图14给出了冲击核心区平均努塞尔数随排布角度的变化。由图14可以看出，冲击核心区靶面的平均努塞尔数先随着排布角度的增大而增大，在排布角度为20°时达到峰值，比排布角度0°时增大了21%，随后呈现减小趋势。当排布角度较小时，在排布角度引起的倾斜流动和增强的对流换热效果的共同作用下，靶面的平均努塞尔数增大。而当排布角度达到一定值后，其对横流造成射流偏转的修正效果超过了横流本身造成的射流偏转，使得高换热区域逐渐开始靠近上游，因此冲击核心区的平均努塞尔数逐渐减小。

图14 冲击核心区平均努塞尔数随排布角度的变化

4 结 论

(1) 在研究范围内，振荡射流冲击靶面的换热效果主要受两方面影响:横流对振荡射流冲击点整体向下游偏移造成的高换热区域后移，以及由于负压引起的马蹄涡结构导致的强化对流换热效果。

(2) 初始横流在横流强度较弱时会削弱振荡射流强度，降低换热效果。随着横流强度增大，形成的马蹄涡会增强靶面高换热区域换热。但是由于高换热区域的整体后移程度不同，2种排布方式下冲击核心区换热效果随横流强度变化呈现不同的变化趋势。

(3) 射流振荡器以一定角度倾斜排布可以增强靶面的换热效果。在纵向排列、入口雷诺数为21 800、横流雷诺数为14 400的条件下，20°的排布角度可以最大化地强化冲击核心区的对流换热效果。