基于混沌理论的地震诱导近海风力机动力响应研究

2022-02-22牛凯伦闫阳天薛世成李志昊

动力工程学报 2022年2期

牛凯伦，闫阳天，李春,2，薛世成，李志昊，孙康

(1.上海理工大学能源与动力工程学院，上海 200093；2.上海市动力工程多相流动与传热重点实验室，上海 200093)

《新时代的中国能源发展》白皮书指出：风电将在实现碳达峰和碳中和过程中发挥重要作用[1]。截至2020年底，我国风电装机容量达2.8亿kW，居世界首位[2]。在气候雄心峰会上我国宣布到2030年，中国风电、太阳能发电总装机容量将达到12亿kW以上[3]。相较陆上风电，海上风电具有风速稳定、噪声小及风电场可建设空间广等优点，因此风电逐渐将发展重心转向蕴藏丰富风能资源的近海地区[4]。

海上风力机运行过程中，面临湍流风、波浪等复杂环境载荷影响，同时我国风能资源相对丰富的沿海地区多位于环太平洋地震带，高强度地震载荷易对风力机的结构安全性和运行稳定性造成潜在危害[5]。因此，对于海上风力机结构设计研究，除环境载荷作用外，还须考虑地震载荷对其动力特性的影响。

Zuo等[6]通过分析5 MW风力机在湍流风与波浪载荷作用下的动力特性，发现气动阻尼对风力机塔顶位移响应有较大影响。Wang等[7]研究发现，10 MW风力机在极端非线性波浪载荷及湍流风作用下，其动力特性由波浪载荷主导。Sajeer等[8]分析发现，当湍流风气动力与波浪载荷水动力作用频率及方向一致时，对风力机动力特性影响最大。但以上研究仅限于环境载荷对风力机动力特性的影响，未考虑地震作用效果。

针对地震诱导近海风力机动力响应特性研究，国内外学者开展了一系列研究工作。闫阳天等[9]发现10 MW风力机在不同强度地震作用下的动力学响应差异明显。杨阳等[10]通过分析5 MW风力机在湍流风及地震载荷联合作用下的动力学响应，表明塔基的振动响应主要由地震载荷决定。Meng等[11]基于5 MW风力机缩比实验得出湍流风和地震的相互作用会使风力机结构整体响应降低。

以上研究均采用传统数理方法对风力机动力响应进行分析，但作用于风力机叶片的非定常气动载荷与结构相互耦合引起的几何非线性效应和地震、波浪载荷作用下风力机基部动态响应之间的强耦合作用使整机运动响应呈显著非线性特征，若仅采用常规方法对其在极端环境载荷作用下的动力响应时间序列数据进行分析，无法反映其内在动力特征。为此，部分学者提出将混沌理论应用于风力机设计中[12-13]，进而从多角度对多维度强非线性结构动力特性展开研究，以期实现对结构问题进行更透彻的剖析，为结构优化及控制系统建模提供更有效的理论基础。综上，笔者以DTU 10 MW单桩式近海风力机为研究对象，基于p-y曲线法及Winkler土-构相互作用模型建立土-构耦合模型，研究其在地震及环境载荷作用下的动力学响应，同时采用相空间重构定性分析和最大Lyapunov指数定量分析方法，揭示海上风力机动力响应混沌特性，为海上风力机结构抗震设计提供参考。

1 研究对象

1.1 大型单桩式风力机

采用Vestas公司与丹麦科技大学合作开发的DTU 10 MW单桩式近海风力机为研究对象。其主要结构和设计参数如图1和表1[14]所示。

图1 DTU 10 MW单桩式近海风力机模型

表1 风力机主要参数

风力机塔架壁厚随高度的增加呈线性减小趋势，塔基外径为7.665 m，壁厚为34 mm；机舱与塔架连接处塔架直径为5.5 m，壁厚为26 mm。模型材料选用密度为7 850 kg/m3、弹性模量为210 GPa、泊松比为0.3、材料屈服极限为380 MPa的A709结构钢，由于构件油漆、焊接及法兰等因素的影响，材料密度修正为8 500 kg/m3[15]。

1.2 土-构耦合

风力机入土桩基与地基之间弹性模量明显不同，当地震载荷通过地基输入桩基时，两者之间所产生的变形量也存在较大差异，进而产生力的相互作用，即土-构耦合作用[16]。笔者根据美国石油协会(American Petroleum Institute, API)推荐的p-y曲线法[17]和Winkler土-构相互作用模型[18]建立土-构耦合模型，如图2所示。其中,γ为有效重度，kN/m3；φ为砂砾内摩擦角，(°)。

当桩基发生横向位移时，土壤作用力与侧向位移呈非线性关系，且根据针对砂性土不同深度水平承载力推导出的经验公式，砂性土的p-y曲线可表达为：

P=APutanh[kHy/(APu)]

(1)

Pus=(C1H+C2D)γH

(2)

Pud=C3DγH

(3)

Pu=min{Pus,Pud}

(4)

式中：A为经验调整系数，A=(3-0.8H/D)，其中H为桩深，D为桩基外径；P为土壤反力；y为侧向位移；Pu为桩深至H时的极限承载力；Pus为桩深至H时的周向极限承载力；Pud为桩深至H时的径向极限承载力；k为地基反力系数，其值取244.4 kN/m3；C1、C2、C3为系数，由砂砾内摩擦角φ确定，如图3所示。

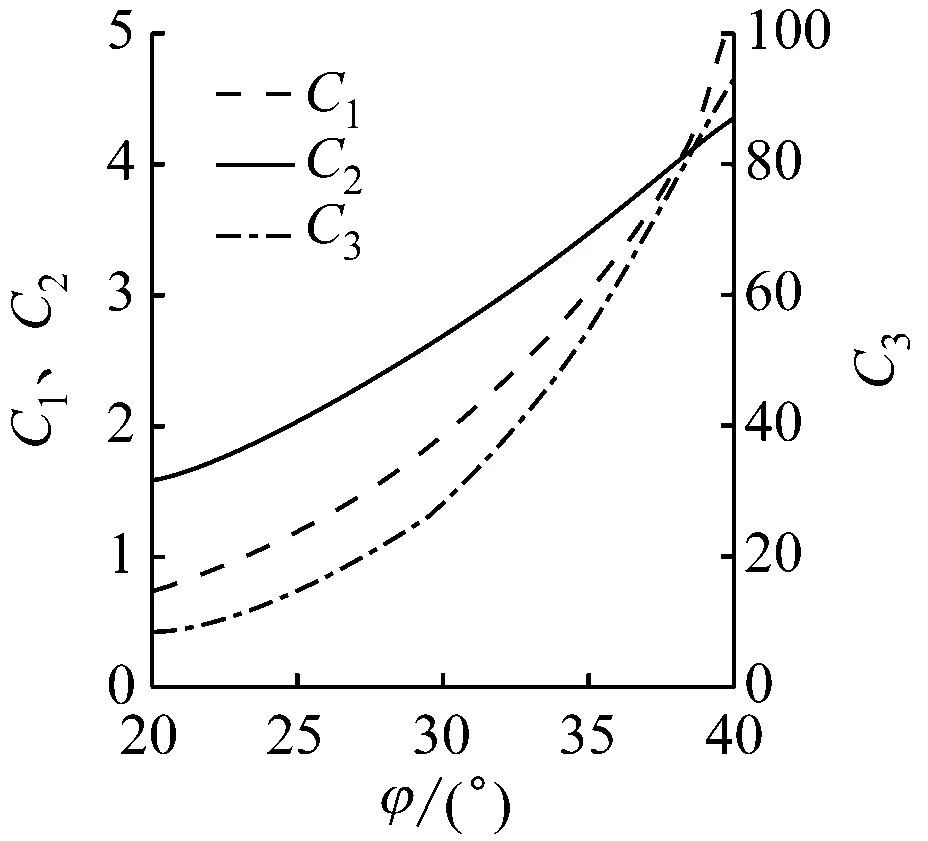
图3 C1、C2与C3系数曲线

计算所得不同桩深处p-y曲线结果如图4所示。

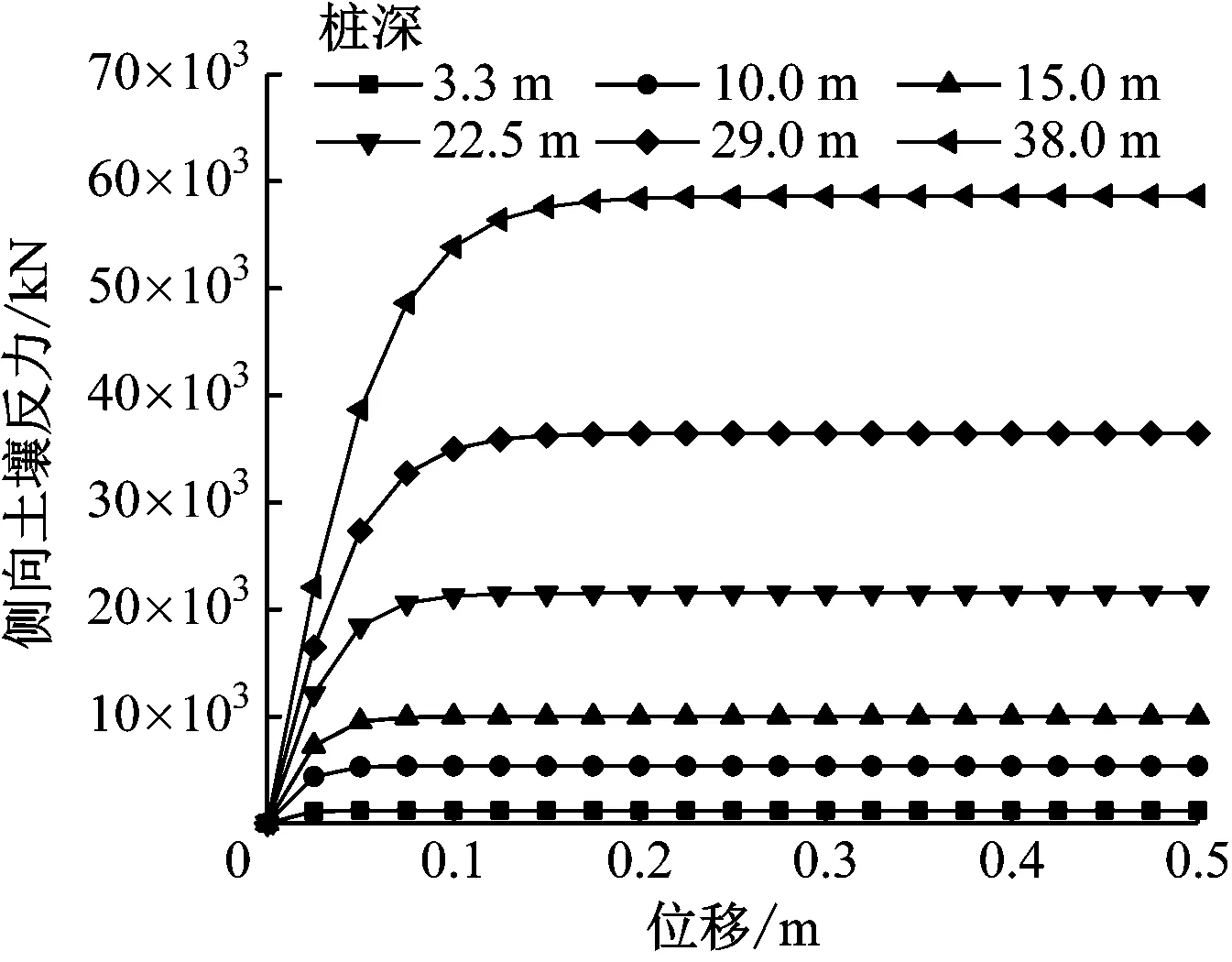
图4 不同桩深处p-y曲线

2 地震及环境载荷

笔者构建了考虑湍流风、波浪及地震载荷作用下的极端环境多物理场非全耦合模型，气动载荷部分通过OpenFAST/AeroDyn求解,波浪载荷在AQWA中生成,地震载荷基于实测近地位移数据产生。

2.1 地震载荷

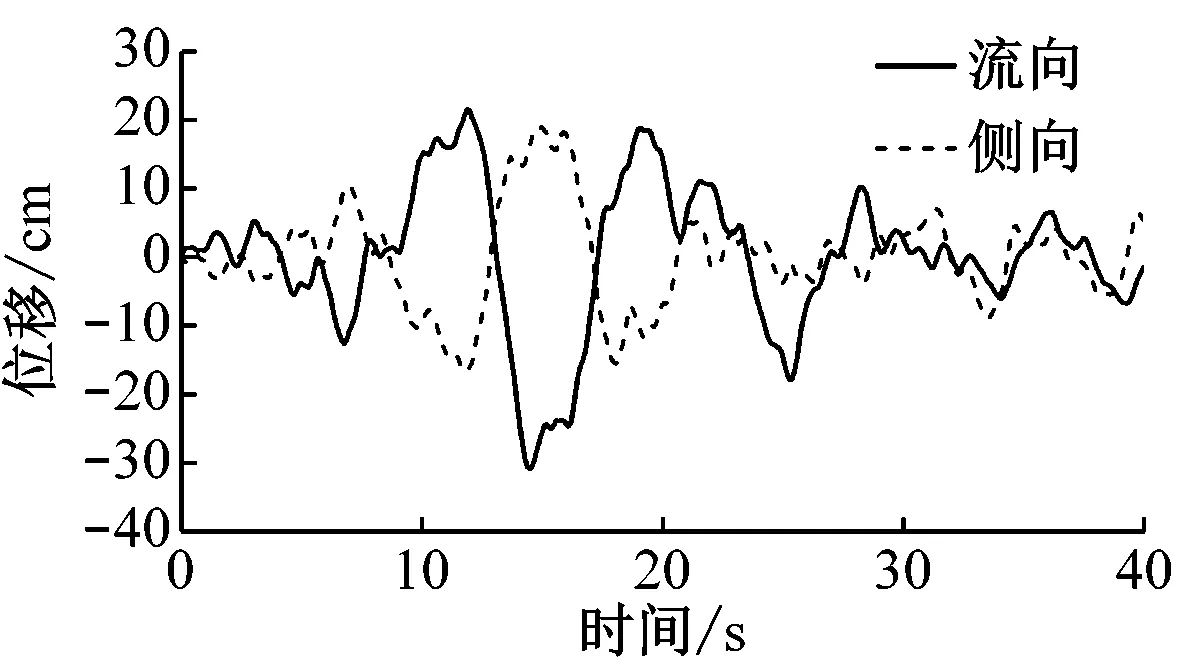
为研究极端环境下不同地震强度与结构响应之间的关系，选用由国家强震动台网中心提供的中国四川2017年九寨沟7.0级、2008年汶川6.0级及2014年越西5.2级地震数据。因我国海上风电场多位于东南沿海，故根据抗震设计规范及东南沿海地质条件[19]，确定以抗震设防烈度为7度，场地类型为Ⅳ，罕遇地震的反应谱对所选地震进行目标谱匹配，匹配后的位移时域曲线如图5所示，7.0级、6.0级、5.2级地震对应的峰值地面位移(PGD)分别为36.20 cm、11.37 cm和7.99 cm。

2.2 湍流风载荷

参照IEC 61400-3设计准则[20]，基于IEC Kaimal湍流风谱模型，风在各方向上的功率谱密度为：

(5)

(6)

其中，湍流尺度参数ΛU为：

(7)

标准差σK等于湍流强度与平均风速之比，不同分量之间的关系定义如下：

(a) 7.0级地震

(b) 6.0级地震

σv=0.8σu

(8)

σw=0.5σu

(9)

由于空间相干模型的存在，u分量的标准差会出现小幅波动。本文风场模型为IECKAI模型，其速度谱(以及标准差)穿过网格时保持恒定值。

通过TurbSim[21]生成平均风速为25 m/s的风场数据，轮毂高度处风速时域变化曲线如图6所示。

图6 湍流风场

2.3 波浪载荷

利用Morison方程计算作用在风力机下部的波浪与海流载荷，Morison方程可以有效地计算出振荡流中作用在圆柱体上的力。

(10)

3 混沌及其判别方法

混沌是指确定性动力系统所表现出类似随机的、不可预测的运动。目前，通常采用定性或定量方法对混沌现象展开分析，常见的定性研究方法有相空间重构法、庞加莱截面法及分频采样法等，常见的定量研究方法有最大Lyapunov指数法、自功率谱密度法和分形维数法等[22]。选取相对成熟简便的相空间重构法和最大Lyapunov指数法对风力机运动响应分别进行定性和定量混沌分析。

3.1 相空间重构法

相空间重构法是研究非线性系统结构特性的成熟方法。笔者基于相空间重构法的基本思想，根据Takens理论和DTU 10 MW风力机的动力学响应时间序列信号，选取合适的延迟时间τ和嵌入维数m，构建出m维相空间，通过相空间中的轨线分布即可反映系统运动规律[23]：(1)若相轨迹趋于一点，则系统处于稳定状态；(2)若相轨迹为一封闭曲线，则系统作周期运动；(3)若相轨迹杂乱无章分布在相空间，则系统作随机运动；(4)若相轨迹具有一定规则，表明系统运动具有混沌特性。

在Takens理论中，对于理想的无限长和无噪声的一维时间序列，嵌入维数m和延迟时间τ可以取任意值，但在实际应用中，因时间序列通常是含有噪声的有限长序列，故其并不能任意取值，否则会影响相空间重构质量，进而影响后续数据处理结果[24]。笔者采用可反映数据点一般相关性的互信息函数法求取延迟时间τ，采用所需数据量相对较小的假近邻法(FNN)计算嵌入维数m。

3.2 最大Lyapunov指数法

针对非线性信号，可通过引入Lyapunov指数λ来判断其是否具有混沌特性。当λ>0时，系统具有混沌特性；当λ<0时，系统不具有混沌特性。λ表达式为：

(11)

4 结果与分析

4.1 时域特征分析

4.1.1 塔架位移

为研究不同地震强度及其与环境载荷联合作用时风力机结构动力学响应特征，计算各条件下塔架位移最大值随塔架高度的变化趋势及塔顶和塔底的位移最大值，如图7和表2所示。

(a) 仅地震载荷

(b) 环境载荷+地震载荷

表2 塔顶和塔底位移最大值

由图7(a)可知，仅有地震载荷作用时，塔架各高度处位移最大值随地震强度的增加而增加，这是由于风力机塔顶质量集中且塔架为细长柔性结构，随地震强度的增加，在惯性及地震载荷共同作用下，塔架摆动程度加剧。

如图7(b)所示，与其他条件下相比，仅有环境载荷作用时塔顶位移最大值最大，为1.519 7 m。当地震及环境载荷联合作用时，随着地震强度的增加，塔顶位移逐渐减小，说明塔顶位移主要为气动弹性效应所导致的柔性变形量，当有地震载荷作用时，可有效缓解环境载荷所造成的塔顶振动。与其他条件下相比,仅有环境载荷作用时塔底位移最大值最小，为0.143 4 m。当地震及环境载荷联合作用时，随着地震强度的增加,塔底位移逐渐增加，说明地震载荷主要影响塔架中部及底部的动力学响应，其诱导塔顶振动幅值较小。

4.1.2 等效应力

在极端环境下，风力机在受到地震及环境载荷等外力作用时会产生较大形变，形变位置会产生应力集聚现象，进而使风力机结构遭受严重损坏。因此，计算塔架在地震及环境载荷联合作用下等效应力达到峰值时其表面等效应力分布情况，结果见图8。

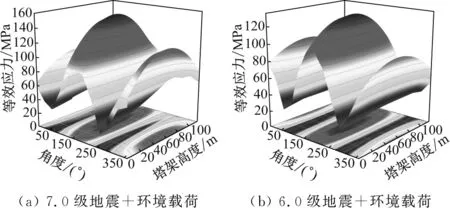
图8 塔架等效应力分布

如图8所示，无地震载荷作用时，塔底等效应力最大，其随塔架高度的增加而逐渐减小。等效应力在流向相较其他方向有更明显的集聚现象,这是由于在环境载荷作用下，塔架变形主要为前后向弯曲变形，因此等效应力在流向较大。有地震载荷作用时，地面震动会缓解一部分因波浪载荷所造成的应力集聚，因此塔架底部等效应力明显减小。随着地震强度增加，塔架变形量逐渐增大，因此塔架中部的等效应力峰值也随之增大。

4.1.3 塔顶加速度

风力机塔顶加速度为反映塔架振动的重要参数，随着风力机朝大型化发展，塔架结构柔性增加，使其在极端环境中易产生较大形变，为检测复杂环境下风力机塔架振动响应，计算不同地震及环境载荷下风力机塔顶流向及侧向的加速度时域曲线，结果如图9所示。

(a) 流向加速度

(b) 侧向加速度

由图9可知，地震载荷对塔顶侧向加速度的影响比对塔顶流向加速度大。塔顶流向加速度主要决定因素为环境载荷，当有地震发生时，塔顶流向加速度沿仅有环境载荷时的加速度曲线上下波动；侧向加速度则以0 m/s2为基线上下波动。因此塔顶流向加速度变化对地震的敏感性相对较小，侧向加速度对地震的敏感性较大。

同时，塔顶侧向加速度峰值大于流向加速度峰值，说明侧向相比流向的振动更剧烈。其主要原因是风轮重心悬垂于塔架中心线，导致塔顶质量在俯仰方向的惯性矩更大，且流向所具有的气动阻尼对塔架流向加速度及位移具有较强的抑制作用，从而在侧向具有更大的加速度。

4.2 混沌特性分析

由4.1.3节可知，风力机塔顶振动伴有明显的随机性和结构不稳定性，因此采用混沌方法对风力机运动特性进行非线性分析。在不同地震及环境载荷联合作用下，风力机塔顶流向及侧向加速度的响应最佳延迟时间τ如表3所示。

混沌的产生是由于系统的整体稳定性和局部的不稳定性共同作用的结果，系统局部不稳定性使其具有对初值敏感的特性，而整体稳定性使其在相空间表现出一定的分形结构，这种结构就称为混沌吸引子[26]。根据相空间重构法绘制风力机在不同地震及环境载荷下流向及侧向加速度时域数据的三维混沌吸引子，如图10和图11所示,其中t为当前迭代时间。

表3 最佳延迟时间

图10 流向加速度混沌相图

由图10和图11可知，塔顶加速度在不同地震及环境载荷下混沌吸引子形态各异，其分别代表了不同状态下塔顶加速度的动力特性。

如图10(a)所示，在仅有环境载荷作用时，塔顶流向加速度的吸引子轨迹反复缠绕形成一种细长“环状”结构。当有地震载荷作用时，随地震强度的增加,吸引子环状区域逐渐稠密，最终形成“团絮状”结构。此现象与图9(a)所示的当有地震发生时，塔顶流向加速度沿仅有环境载荷时的加速度曲线上下波动现象相对应，进一步说明塔顶流向加速度主要决定因素为环境载荷。且由吸引子结构变化规律可知，随着地震强度的增加，塔顶流向加速度响应的混沌特性逐渐增强，塔顶稳定性减弱。

如图11(a)所示，当仅有环境载荷作用时，塔顶侧向加速度吸引子轨迹反复缠绕成“棒状”结构。当有地震载荷作用时，其吸引子轨迹纠缠发散成盘状，且随着地震强度的增加，其波动轨迹逐渐扩散加密，说明随地震强度增加，其塔顶侧向加速度混沌特性逐渐增强，塔顶稳定性减弱。