基于人工结构板的声贝塞尔束的相位调控（特邀）

罗立成，李恒毅，柯满竹，刘正猷

（武汉大学物理科学与技术学院，武汉430072）

0 引言

物理学中，涡旋光束及其所携带的轨道角动量（Orbital Angular Momentum，OAM）是声光等领域的重要研究课题。1989年，COULLET P 等受到流体动力学涡旋束的启发，发现了麦克斯韦-布洛赫方程的一个解，并提出了涡旋光束的概念［1］。1992年，ALLEN L 等提出了近轴传播涡旋光束中的轨道角动量概念，揭示了宏观光学和微观量子效应之间的关系［2］。正是OAM 所具有的高保密性、高信息密度的特性，使得其越来越受到人们的关注并被研究，例如利用携带OAM 的涡旋光束实现的显微观察［3］、超衍射极限成像［4］、信息的编解码［5-7］以及光通信［8-9］等。在声学领域中涡旋束也受到了广泛关注［10］，例如进行粒子操控［11-12］以及进行信息传递。尽管现在利用电磁波、光等手段进行信息传输更为常见，但是在海洋通讯等水下领域，电磁波和光等通讯手段由于传播过程中衰减较快，很难进行远距离的信息传输。由于在水中声波衰减相对较慢，声通讯在水下得到了广泛的应用。而声波作为压力波，不存在电磁波中的自旋、偏振等物理特性，因而无法基于这些特性拓展信道容量。角动量作为独立于时域和频域的新自由度，携带角动量的涡旋束有望在声通讯中使声波在同一频率下传递更多信息，提高信息传递速率，因此对角动量的调节在利用其进行信息编解码的过程中有应用价值。2017年，张翔教授课题组便演示了使用具有8 个不同拓扑荷的声涡旋场对英文字符进行编码与解码的过程［6］；2018年，程建春教授团队则进一步利用声波的角动量实现了多路复用的实时信号传输［13］。贝塞尔束具有能量高局域、非衍射的特点，在任意截面上，贝塞尔束可以用Jl(μr)eilθeiκz来描述，l代表贝塞尔束的阶数，对于l阶贝塞尔束，绕其光轴一周的相位变化为2πl，θ为方位角，非零阶的贝塞尔束携带有OAM。由于加工工艺的限制，单个点源的尺寸无法做到太小，因而得到的涡旋束也有最小尺寸限制。第二种产生涡旋束的方法是利用亥姆霍兹共振腔［15］，这种方法的不足在于，共振腔的截面积与长度都必须达到半波长，例如在空气中使用1 kHz 的声波来激发涡旋束时，装置的长度需达到17.15 cm。第三种方法是通过声人工结构产生对应波束［16-20］，这种方法便于根据目标调节结构参数，同时对激发源的要求也相对较低，因而得到了越来越多的关注。

本文基于第三种方法，设计了一个具有镂空阿基米德螺旋栅的金属板，理论推导了平面波与非零阶贝塞尔束入射到该人工结构板后出射场的声场分布，以及将入射波频率提升至人工结构板对应基频倍数后的效果。

1 理论模型

1.1 平面波入射理论的推导

当平面波入射到镂空螺旋栅的时候，螺旋栅上每一点都可以看作是次级点源，如图1 中螺旋栅上的一点r(r，φ)。由平面波的表达式p=p0exp(ikz z)可以得到，点r对观测点R(R，θ)的声场贡献为［21］

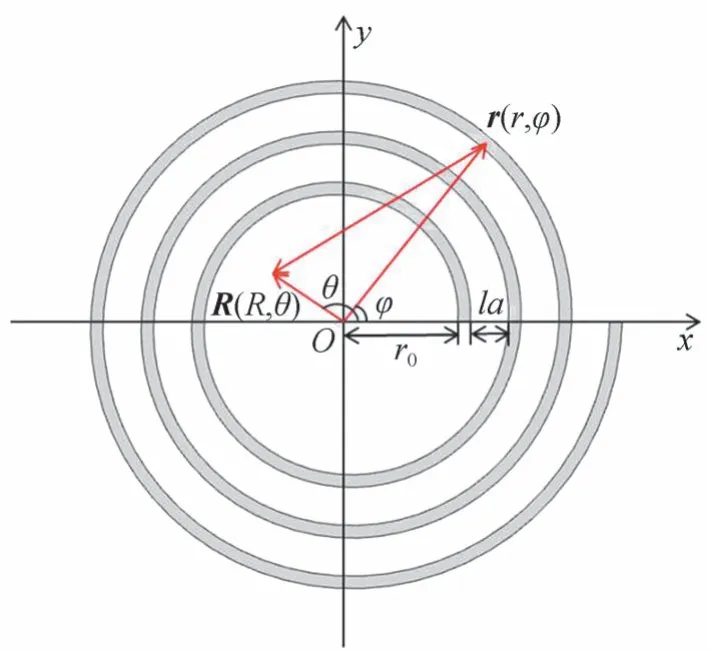
图1 阿基米德螺旋栅示意图Fig.1 Scheme of Archimedean spiral grating

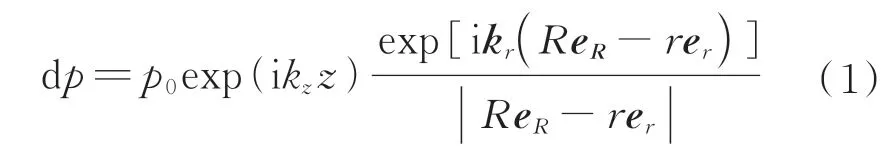
式中，exp(ikz z)是沿z方向的传播因子，基频下波长等于a，同一螺旋线上相邻两环在径向对应两点的距离为la；l是螺旋栅的阶数，基频下l=1；φ表示方位角，点r处由入射波激发出沿径向的一级衍射波，对应波数为，r与φ的关系为，其中，r0为常数，表示螺旋栅的初始半径。

根据惠更斯原理，中心区域所获得的声场，可以看作是所有次级点源贡献的叠加。当满足R≪r条件时有|ReR−rer| ≈r，且eR·er=cos(θ−φ)，由此在观测点R(R，θ)的声场分布为

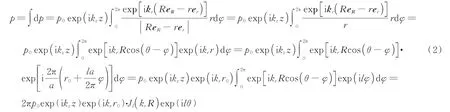
根据以上推导，用平面波入射，得到的声场具有l阶贝塞尔束的形式，因此螺旋栅上相邻两环在径向对应两点间的距离与入射波波长的比值，即为所得贝塞尔束的阶数。这提供了两种进一步提高出射波阶数的办法，一种是升高频率至基频的倍数；另一种方法是加大螺旋栅相邻两环间距至原波长的倍数，这种方法需要改变原有结构。

1.2 贝塞尔束入射

将入射波由平面波改为阶数为n的贝塞尔束，其径向波数为μ，z方向波数为κ，这两个方向的波数满足k2=μ2+κ2。入射波具有p=p0Jn(μr) exp(inφ)exp(iκz)的形式，且镂空阿基米德螺旋栅平行于x-y平面。因此，入射波在r点产生的场强为p0Jn(μr) exp(inφ)exp(iκz)。点r对观测点R的声场贡献为

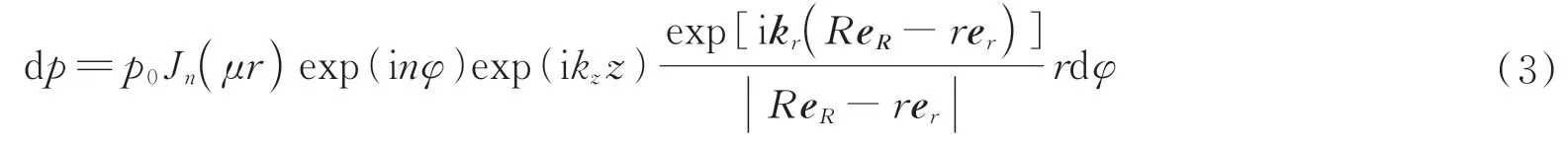
类似地，在观测点R(R，θ)的声场分布为

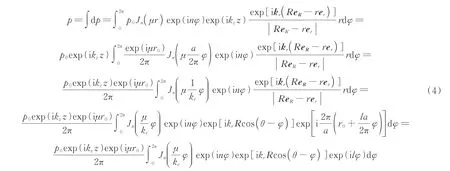
由分部积分法和贝塞尔束积分公式

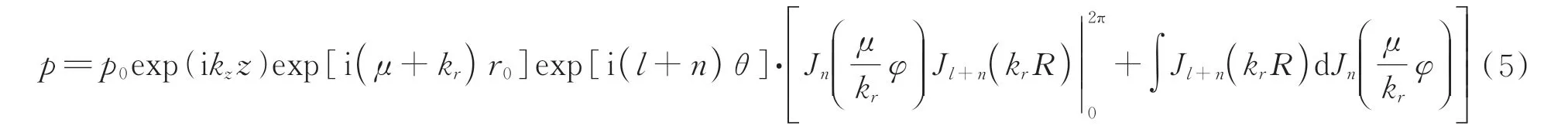
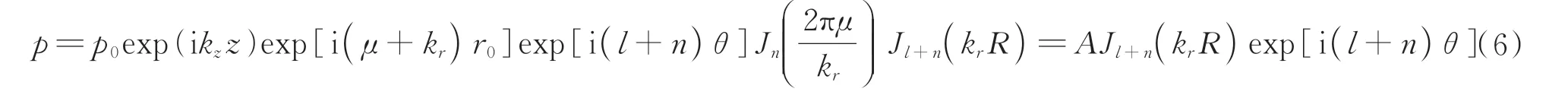
在上述的推导过程中，使用了两次近似：第一次是R≪r，即观察的场点的径向距离远小于源点，对应到结构参数上表现为，在获得的贝塞尔束阶数足够高的情况下，r0也要足够大；另一次是μ≪kr，即入射贝塞尔束的径向波数要足够小，才能在表面产生线性叠加。

2 数值模拟

本文中，利用有限元仿真软件Comsol Multiphysics 中的压力声学、固体力学模块进行模拟计算。模型如图2所示，上下蓝色部分为水，使用压力声学模型计算，中间黄色的部分为刻有顺时针阿基米德螺旋栅的金属板，使用固体力学中的线弹性材料计算，水层外侧以辐射边界包裹，结构板边缘为低反射边界，网格最大单元大小为对应频率下波长的三分之一。从顺时针螺旋栅一侧入射称为正向入射。板厚度为0.5 mm，半径r=12 mm，螺旋栅起始半径r0=4.5 mm，镂空部分w=0.5 mm，相邻格栅间距a=1.5 mm，水的密度ρ=1 000 kg/m3，声速c=1 500 m/s，当入射波的频率f=1 MHz 时，波长λ=a=1.5 mm，此时在板表面生成1 阶贝塞尔束。

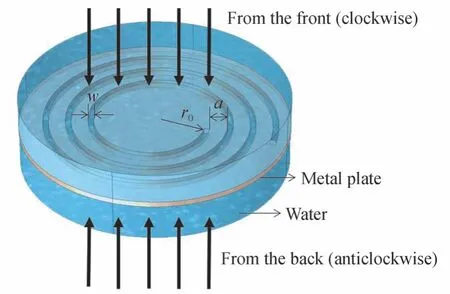
图2 数值模拟中的模型Fig.2 Scheme of the model in numerical simulation

图3（a），（d）是工作频率对应结构的基频频率f=1 MHz 下，平面波从正（顺时针，（a））反（逆时针，（d））两向入射到阿基米德螺旋栅的出射波声压及相位分布，结果如预期一样，正向入射到螺旋栅后得到了+1 阶贝塞尔束，反向入射到螺旋栅后则得到−1 阶贝塞尔束。这验证了在1.1 中的理论推导。同时，利用+1 阶贝塞尔束从正反两向入射（如图3（b），（e）），分别得到了+2 阶（1+1）、0 阶贝塞尔束（1−1）；−1 阶贝塞尔束入射（如图3（c），（f）），则分别得到0 阶（−1+1）、−2 阶贝塞尔束（−1−1）。这验证了1.2 中贝塞尔束入射情况的理论推导：在满足相应的近似条件的情况下，出射波是入射波与板结构导致的声场的线性叠加。

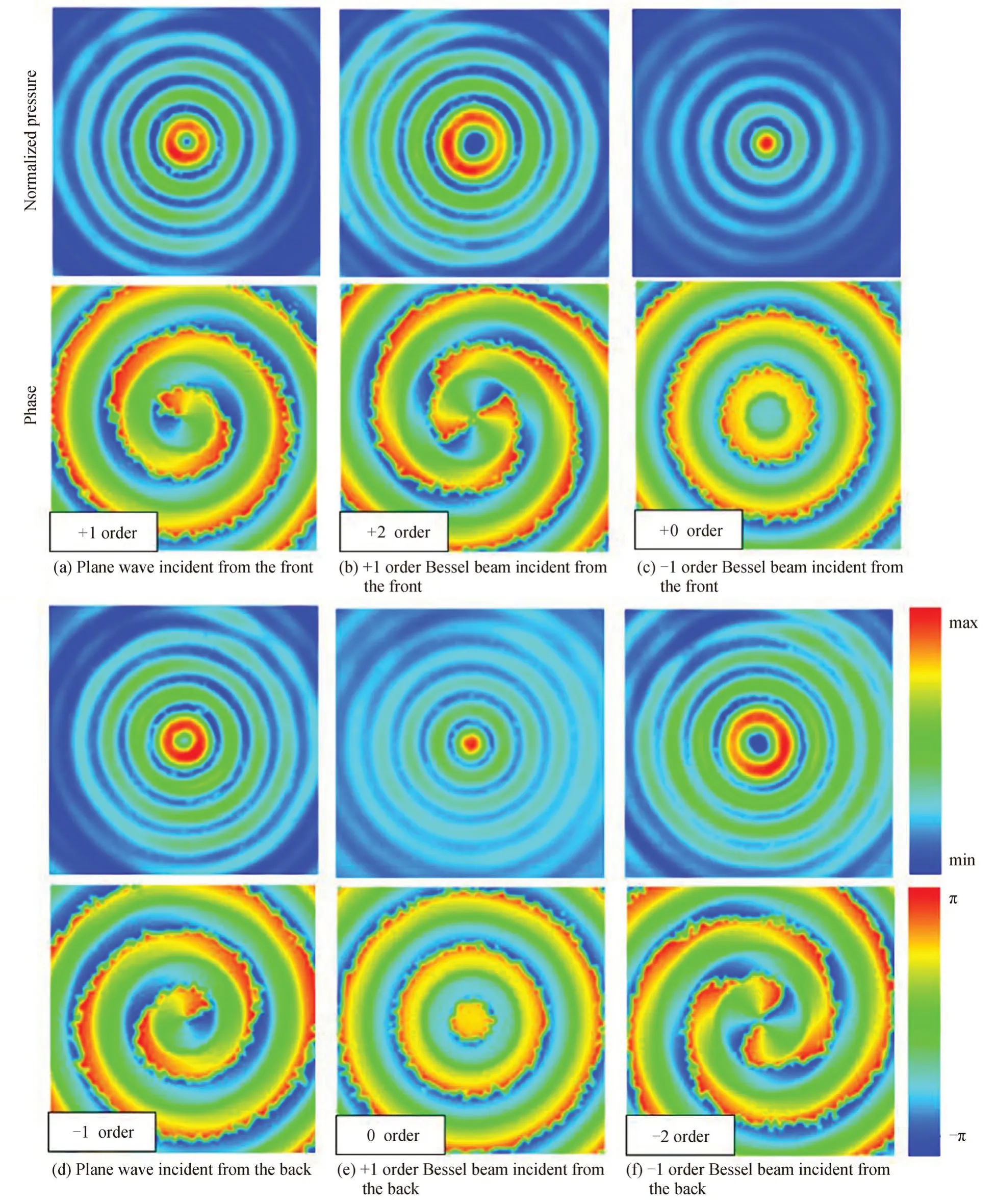
图3 频率f=1 MHz 下，不同入射波的出射波声场分布Fig.3 Numerical pressure and phase distribution of output wave for different incident wave at the frequency f=1 MHz

同时，为了显示对高阶入射声束的调控，数值模拟了不同阶数贝塞尔束从正（顺时针）向入射至螺旋栅结构板后的出射波声场分布（上排为声压分布，下排为相位分布）。如图4（a）～（c）是−8、−6、−4 阶贝塞尔束入射后被结构板调控的出射波为−7、−5 和−3 阶贝塞尔束；图4（d）～（f）展示的是+3、+5、+7 阶贝塞尔束入射后被调控的出射波为+4、+6 和+8 阶贝塞尔束，这说明1.2 中的理论也适用于高阶贝塞尔束。另外，从出射声场的声压分布可看出，除了零阶贝塞尔束不存在中央场强为零的区域，贝塞尔束阶数越高，中心区域场强为零的区域宽度越大；这为利用声场进一步操控粒子等提供了参考。需要说明的是，由于模拟过程中螺旋栅尺寸有限，不同手性的出射波内环声压能量会聚集在不同位置，提高螺旋栅的环数或初始半径可提高内环声压分布的均匀性。

上述提到，改变结构参数或工作频率可灵活调控入射波的阶数，比如两倍甚至高倍的改变相位。首先改变入射波的工作频率来展示其调控效果。如图5（a）和图5（d）所示，将入射波频率提升至基频的两倍，即f=2 MHz，此时用平面波从正（反）向入射到螺旋栅，如期得到了+（−）2 阶贝塞尔束，即出射声束阶数两倍的增加或降低。图5（b）和图5（c）也展示了两个非零阶贝塞尔束入射后的调控效果：+1 阶贝塞尔束从正向入射到螺旋栅会得到+3 阶贝塞尔束，反向入射会得到−1 阶贝塞尔束；−1 阶贝塞尔束从正向入射到螺旋栅会得到+1 阶贝塞尔束，反向入射则会得到−3 阶贝塞尔束。然后，将螺旋栅栅格间距调整为原来的两倍，即a=3 mm，并用平面波从正（反）向入射，如图6（a）与图6（b）所示，也同样得到了+（−）2 阶贝塞尔束。上述结果表明，在不改变入射贝塞尔束阶数的情况下，可以通过提高入射波频率至人工结构板基频的倍数或将格栅间距增加至基频下波长倍数来得到高倍数的相位阶数调控效果，进而实现对贝塞尔束阶数更灵活的调控。

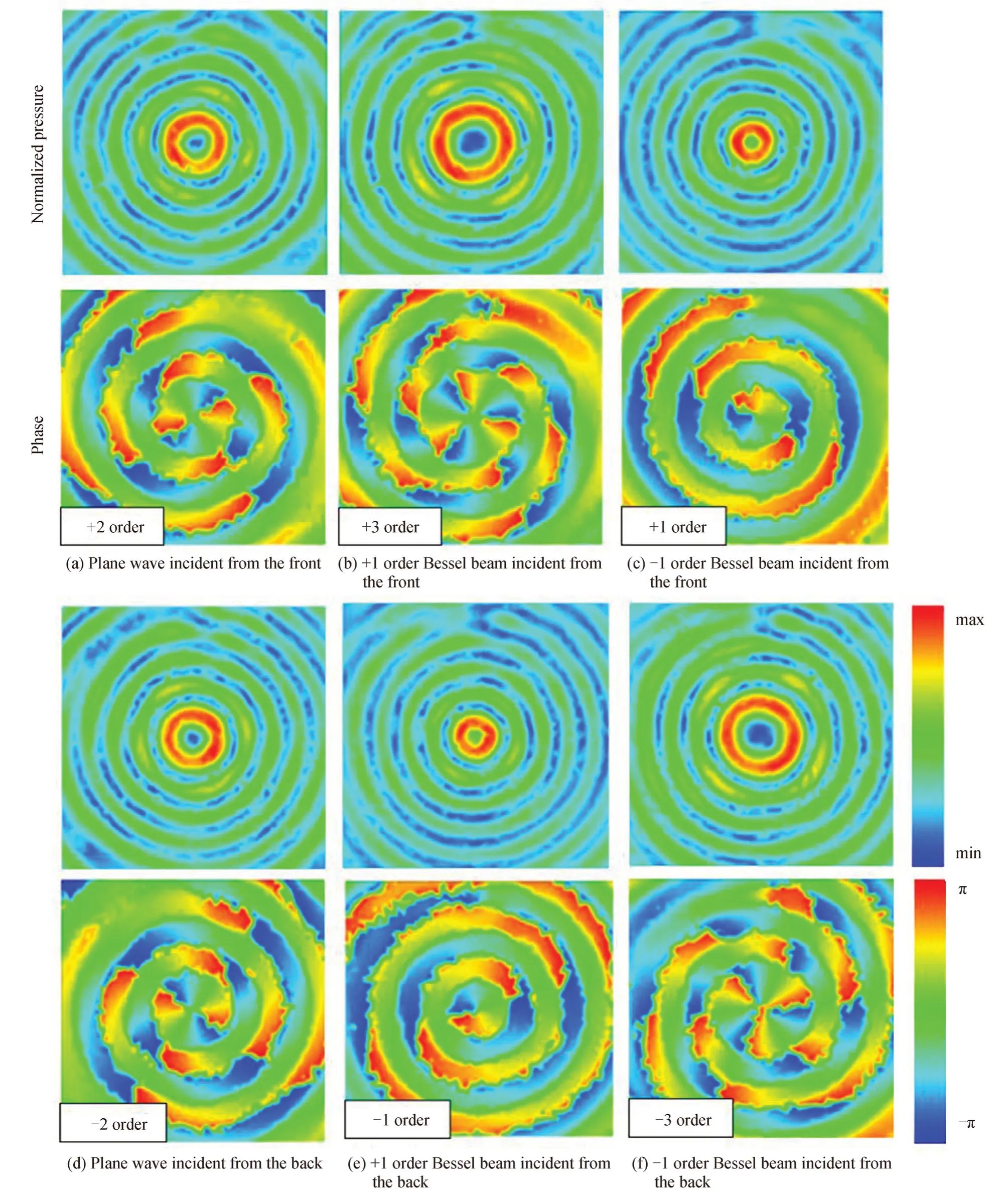
图5 频率f=2 MHz 下，不同入射波的出射波声场分布Fig.5 Numerical pressure and phase distribution of output wave for different incident wave at the frequency f=2 MHz

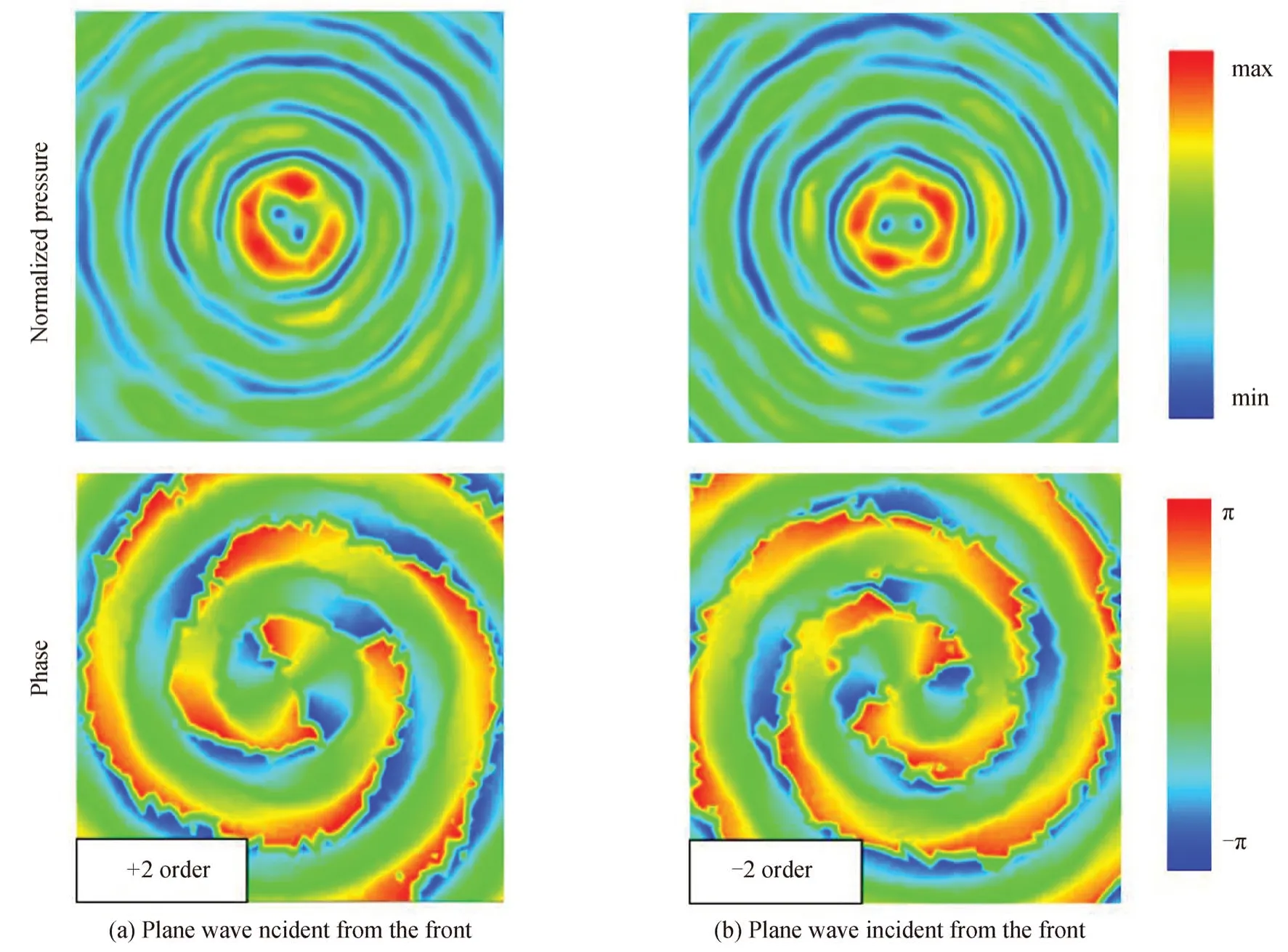
图6 频率f=1 MHz 下，平面波波入射到格栅间距为a=3 mm 的镂空螺旋栅后的出射波声场分布Fig.6 Numerical pressure and phase distribution of output wave for incident plane wave which travel through the hollow spiral grating with a=3 mm at the frequency f=1 MHz

3 结论

基于惠更斯原理推导了平面声波及声贝塞尔束入射到具有镂空阿基米德螺旋栅的金属板后的声场分布。结果表明，从正反两向入射到具有合适参数的镂空螺旋栅，平面波的出射波分别为具有相反拓扑阶数的贝塞尔束；贝塞尔束入射后调制的出射波分别为升阶或降阶的贝塞尔束。进一步，通过提高入射波频率至基频的倍数或将格栅间距增高至基频波长的倍数，可获得对入射波更高倍数相位的调控能力。这些结果通过数值模拟得到了验证。镂空螺旋栅结构板所具有的这些特性使得它可以调节声波的拓扑阶数，在利用角动量进行信息传输以及编解码上具有应用前景。