超表面结构MEMS红外超窄带光源研究

邹宇，蒋文静，欧文

（1 中国科学院微电子研究所，北京100029）

（2 中国科学院大学，北京100049）

0 引言

红外光源是一种非照明光源，广泛地应用于大气通讯、化学检测、气体成分检测等领域［1］。常用的红外光源主要分为红外发光二极管（Light-Emitting Diode，LED）光源、红外激光光源以及红外热辐射光源。而微机电系统（Micro-Electro-Mechanical System，MEMS）红外热辐射光源因为其体积小、工艺简单、功耗低、成本低等优点成为了研究的热点。但是MEMS红外热辐射光源属于类灰体［2］，存在光谱分布范围比较广、波峰的位置会随温度变化、发射率比较低的缺点。在化学检测和气体成分检测领域，只需要特定波长的红外光，MEMS 光源的光谱分布范围比较广会徒增功耗，还会影响检测的灵敏度。目前改进MEMS红外光源的方法主要是在光源表面附加一层微纳结构，主要包括纳米硅结构［3-4］、光子晶体［5-6］、光栅［7］以及超表面［8-9］等。其中纳米硅结构能显著提高发射率，但是其光谱分布范围依然很广。光子晶体能够实现选择性的发射率，但因为其非共振特性，光源没有非常尖锐的波段或高发射率，因此没有显着提高效率［10］；光栅也能实现选择性发射，但带宽略宽。在超表面中，可以对结构形状、几何尺寸和材料厚度进行调整，不仅可以实现任意红外波段的高发射率的调节，还能实现对频带宽度的调节。在超表面结构中，十字结构因为能够实现窄带宽和角度无关性而备受青睐，但是国内目前对它在光源方面的应用研究还不多。

本文针对十字结构型超表面提出了一种改进的RLC 模型用以预测光源的峰值波长、发射率和带宽，从而避免耗时的数值优化问题。不同于前人的模型［14-15］，本文模型不仅没有针对电场和磁场不均匀分部而引入复杂的等效尺寸，还通过引入一对等效电感对十字形和“—”字型结构加以区分。本文还通过仿真探究了十字型超表面十字结构长宽高和结构周期、介质厚度、底层金属厚度六个尺寸对光源峰值波长、发射率和带宽的影响，并与模型中的对应关系进行对比。

1 基本原理

MEMS红外光源是一种微型化的非照明光源。它通过外接电压加热电阻产生焦耳热成为高温辐射体。与黑体类似，加热的温度会影响MEMS红外光源的发射谱。在成分检测领域，过宽的带宽不但会降低灵敏度，还会因为其他成分对其他波长红外光的吸收导致测量不准确。需要一种光学结构将MEMS红外光源转化为有选择性、窄带、高发射率的光源。而超表面对电磁波的具有调控作用，能够很好地完成这一任务。

应用超表面的MEMS红外光源结构如图1，MEMS红外光源以热辐射的形式将电磁波传递给超表面。根据惠更斯原理，超表面就会成为新的电磁波发射源，光源的特性就由超表面的特殊结构决定。

图1 应用超表面的MEMS红外光源示意图Fig.1 MEMS infrared light source using metasurface

超表面结构能够实现对光源调控是因为它对红外波段的光具有电磁共振响应。电响应可以靠细金属周期阵列来实现。对材料结构尺寸进行设计能够实现对红外波段电磁波的磁响应［11］。其中顶部金属图案的几何形状和尺寸对共振响应的影响巨大［12］。

电响应和磁响应的频率和强度都会受金属的等离子体频率影响。因为金属等离子体频率的不同，应用于上下表面的金属材料在各个电磁波段都不相同。在中红外波段，上下表面合适的金属只有金、银、铜。由于银容易氧化，而金和铜的化学稳定性良好，所以一般情况下会选用金和铜作为上下表面的金属材料。

材料选定之后，超表面的电磁响应特性就依靠各种结构的调整。超表面吸波器或者发射器采用的是图形化金属层-介质层-金属层结构。如图2，光传播到这种结构的表面时，其中一部分会引起一种电子与光子的集体震荡，也就是表面等离激元。这部分被束缚在表面的电磁波因为欧姆效应能量逐渐耗尽会被金属以及相邻的介质吸收或者被重新辐射出来［13］。在吸波器中，上表面照射的电磁波主要是被耗尽吸收。而作为发射结构时，上表面主要是重新辐射共振波段的电磁波为主。MEMS 加热模块热辐射传播的相同波段电磁波会在超表面中共振并辐射，其他波段的电磁波会被底层金属层反射回去，从而实现有选择性、窄带宽以及高发射率。

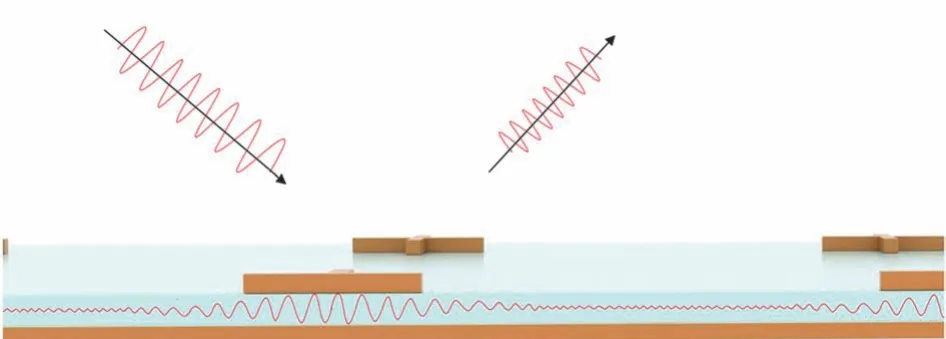
图2 光在金属-介质-金属结构超表面的传播Fig.2 Propagation of light on super-surface of metal-insulator-metal structure

结构的调整会改变辐射电磁波的共振中心频率、共振强度和共振频率范围，分别影响光源的选择频率、发射率和带宽。选择频率由峰值波长评价，带宽则主要用FWHM（Full Width at Half Maxima）来评价，FWHM 越小，带宽越窄。

2 模型建立

超表面发射结构不需要对光的相频等特性进行分析，等效介质理论不再具有优势。本文使用等效电路理论进行分析，等效电路理论不仅能够反映出光源的特性，还能体现出电磁波在结构中谐振的特性。在等效电路理论中，超表面的等效分步电阻、电感、电容决定了等效阻抗。

之前的模型［14-15］对十字结构和“—”字结构无法做到区分，而且引入了一些复杂的等效尺寸。本文针对之前的应用于十字形结构的RLC 等效电路模型提出了改进。改进的模型包括金属-介质-金属结构等效的RLC 振荡电路。RLC 振荡电路包括上下金属层的之间的电容和互感以及上下金属层的电阻和电感。等效模型如图3。

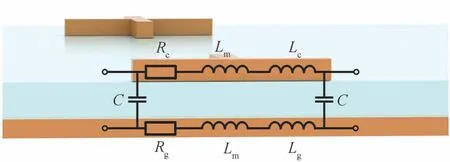
图3 等效模型示意图Fig.3 Schematic diagram of equivalent model

超表面结构如4 图，p是周期长度，l、w分别为十字结构的长和宽，tox为中间介质层的厚度，tc为十字结构金属厚度，tg为底部金属厚度。

图4 结构尺寸示意图Fig.4 The structure and size of the model

本文选择金作为上下表面的材料，中间介质层选用氧化铝。对金采用修正Drude 模型［11］，模型中取等离子频率为1.354×1016rad/s，碰撞频率为1.836×1013Hz，ε∞为9.068 5。氧化铝材料的相对介电常数取9.9。在金属电子气的Drude 模型中，金属电导率会随着外加电磁场频率的变化而变化，满足关系式［11］

式中，σ0是金属的直流电导率，。类比电阻率与电阻的关系式，十字结构中的“—”字结构金属的阻抗可表示为

式中，τAu是金的弛豫时间，与碰撞频率互为倒数；ωp是金的等离子体频率，；δAu是金的趋肤深度，；κ是金的复折射率的虚部，代表消光系数。1～12 μm 范围内金的消光系数［16］经过数值拟合可近似为。

将阻抗关系式中的实部虚部分开来表示，十字形顶层金属的一条臂的电阻和电感可以表示为

同样，将金属底板的尺寸参数代入式（3），可得到底部金板的等效电阻电感参数

Cm是上下两个极板之间的电容，分为左右两个部分，根据平板电容的计算公式，可以得出

Lm是上下两个金属结构之间的互感［14］，表示为

考虑十字结构另外两个臂的电感效应，那么谐振电路的总阻抗为

整个电路主要是并联谐振，此时Ztotal的分母虚部应为零［16］，令Ztotal=0，可以求解得到

那么峰值波长为

式中，c为空气中的光速。根据品质因数Q与损耗因子的关系［19］可以得到等效电路的品质因数

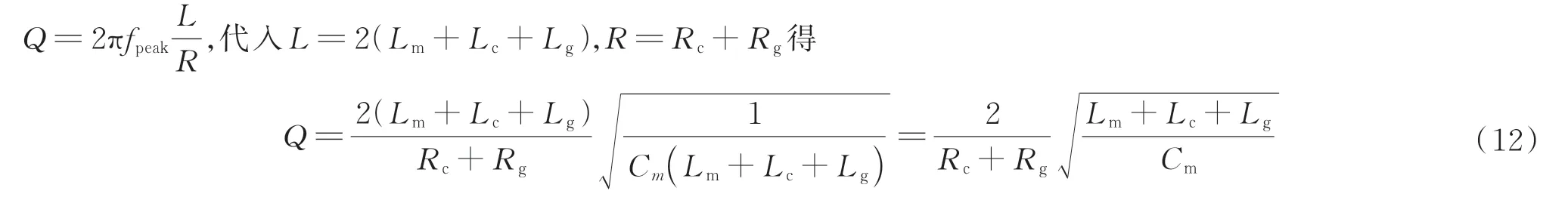
该结构波长域的发射光谱关于峰值波长对称，波长域Q值与频域Q值基本相等，半高全宽可以近似为

3 模型和仿真的对比与分析

为了对比模型中关键尺寸对光源的峰值波长、发射率和频带宽度之间的关系与实际情况的差异，本文先使用FEM 仿真软件对超表面结构进行仿真。分别改变l、w、p、tc、tg、tox中一个参数并固定其他5 个尺寸进行仿真，关键尺寸与光源的峰值波长、发射率的关系如图5。

因为金属存在趋肤效应，当tc和tg增大到一定厚度之后对λpeak基本没有影响。但是tc的厚度会影响发射率的大小，这是因为束缚界面距离结构表面的距离太远。介质厚度增大到一定厚度之后对λpeak也基本没有影响，但它同样也会影响发射率的大小，主要是tox的增大减弱了上下基板之间的磁分量响应。

w和p的改变虽然会使峰值波长上下波动，但峰值波长只是在较小范围内波动，所以w和p对峰值波长的影响可以忽略不计。但w和p对发射率的影响却十分明显，可以通过改变它们的尺寸对发射率进行调节，实现任意波段的高发射率。

λpeak近似与l线性相关，而l的改变在一定范围内对发射率的影响不大。除l之外，其他5 个尺寸的修改对峰值波长的影响可以忽略，所以l尺寸可以独立调整峰值波长的大小。

取图5 仿真结果中发射率大于96%的尺寸，分别测量它们的FWHM，FWHM 与6 个关键尺寸参数单独调整时的关系如图6。FWHM 主要受三个因素的影响，分别是十字结构长度、介质厚度和周期大小。FWHM 随着l的增大逐渐增大，近似于跟l2成正比，但增大速度略小于l2。tox的增大也会导致FWHM 增大。但l还影响着峰值波长的调节，tox和p也决定着发射率的大小，所以只能在很小的范围内调节尺寸来改变FWHM。

图5 峰值波长和其对应发射率与各个尺寸的关系Fig.5 The relationship between peak wavelength and emissivity of the peak wavelength and each size

图6 不同关键尺寸对FWHM 的影响Fig.6 The influence of different key size on FWHM

6 个关键尺寸在小范围内的改变对发射率、峰值波长以及FWHM 的影响都很小。这意味着该结构对加工工艺精度的要求不是很高。

将模型中峰值波长、FWHM 与l的关系与仿真数据进行对比，结果如图7。在模型中，Lm、Cm和Lc都正比于l，那么λpeak就正比于顶层十字结构的长度，可以通过增大十字结构的长度来增大峰值波长，这与仿真结果一致。模型和仿真中FWHM 随l的变化关系也基本吻合。

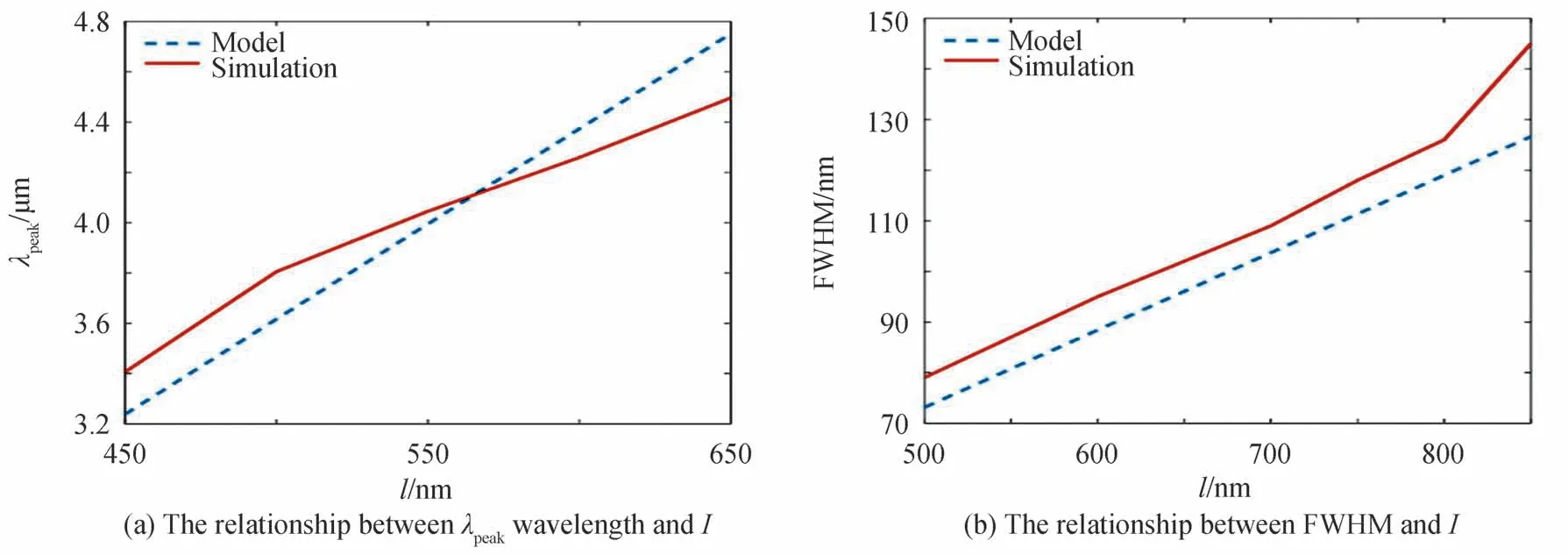
图7 模型和仿真关于l 对光源性能影响的对比Fig.7 Comparison between model and Simulation about L′s influence on light source performance

在设计尺寸l=550 nm，w=80 nm，p=2 000 nm，tc=80 nm，tg=60 nm，tox=100 nm 时，模型计算的阻抗和发射率与波长的关系如图8，在峰值波长时，Ztotal=400.1−37.15j=(1.167−0.099j)Z0，发射率为99.2%，峰值波长为3.994 μm，FWHM 为81 nm。与仿真数据（λpeak=4.04μm，A=99.7%，FWHM 为87 nm）基本一致。

图8 仿真结果的阻抗分析Fig.8 Impedance analysis of simulation results

理论上，在等效阻抗的虚部为0，实部为377 Ω 时，发射率最大，但是仿真结果与等效模型中都只能无限接近却达不到1。这是因为存在两个地方的谐振，第一个是串联支路的RLC 串联谐振，另一个是两条支路并联在一起的并联谐振。由于另一条不发生串联谐振的支路存在电感，那么两者谐振频率必然不同，所以当发生并联谐振时，模型的总阻抗虚部不为零，也就会降低整个系统的发射率，使得发射率会永远小于1。

在对比过程中，该模型预测的光源性能与仿真结果一致，仿真中反映的光源性能与关键尺寸之间的关系也可以用模型中的理论解释。在设计过程中可以先使用模型计算出设计尺寸的范围，然后再用仿真软件进行细节调整，能够在很大程度上节省盲目调整花费的时间，避免复杂的数值优化。

4 结论

十字结构型超表面能够极大地提高MEMS红外光源的发射率，并能够实现选择性的窄带宽。因为其共振的特性，对加热温度的依赖性不高。根据仿真结果来看，这种结构中尺寸小范围内更改对光源的峰值波长、发射率和带宽影响不大，因此该结构对加工误差的要求较低。

本文改进了一种RLC 模型，在该模型中，能够清楚地看到各个尺寸对光源性能的影响。可以通过修改l的长度来调整峰值波长，通过修改w和p来实现高发射率，遗憾的是，l尺寸的更改不仅会影响到峰值波长的移动，还会改变FWHM 的大小，FWHM 也没有单一的结构尺寸可以对其独立调整。这种规律与仿真数据基本一致。

该模型还能够比较准确地预测峰值波长所在的位置、对不同的材料也有适用性。不同于之前的模型［15］，该模型能够对上层金属板“+”和“-”字型结构通过附加电感加以区分，也不需要针对材料中电场和磁场的不均匀分布，使用等效尺寸计算模型中的等效阻抗。本文模型能够快速地计算出发射率，无需耗时的数值优化，能够大幅度减少设计时长。

本文还根据模型设计了一种峰值波长为4μm、发射率为99.7%，FWHM 仅为87 nm 的窄带光源。将该尺寸发射光谱的模型计算结果与仿真进行对比，证明了模型对光源光谱的预测性。