光场纵向调控研究进展(特邀)
2022-02-22李鹏樊鑫豪李渝刘圣魏冰妍赵建林
李鹏,樊鑫豪,李渝,刘圣,魏冰妍,赵建林
(西北工业大学物理科学与技术学院陕西省光信息技术重点实验室,西安710129)
0 引言
自1960年第一台激光器发明以来,以激光为支撑的基础科学研究、技术开发和工程应用得到了飞速发展,使得光学这一古老学科焕发了青春,迈入了全新的激光时代。近年来,随着对激光基础和技术应用研究的不断深入,尤其是通过调控光场振幅、相位和偏振态的空间分布,涌现出了一系列具有新颖光学性质的空间结构光场[1-8],在解决光波技术瓶颈方面展现了巨大的潜力。同时,围绕对此类光场的研究,还揭示了诸多新的物理现象和效应[9-15],更进一步推动了光场以外的其它物理场调控理论和技术的发展。
相位作为光场的重要参量之一,在光的传播、干涉、衍射等动力学过程中发挥着关键作用。在光场中,相位奇点因其特殊的空间结构和强度特征而被长期关注。1989年,COULLET P 在研究激光模式时引入了“光学涡旋”这一概念来描述此类奇异点[16]。作为亥姆霍兹方程本征解,具有螺旋波前和相位结构的涡旋光束,展现了不同于传统球面波和平面波的强度分布及动力学特性。1992年,ALLEN L 揭示了涡旋光束具有内禀轨道角动量(Orbital Angular Momentum,OAM)特性[17]。由OAM 所带来的动力学性质和量子性质,使得涡旋光束在微粒操控、高容量高速率的大规模光通信、量子信息处理、超分辨显微成像等许多领域展现出重要潜在价值与应用前景[10,12],吸引了人们越来越多的关注与研究兴趣。
偏振作为光场的基本属性之一,在光与物质相互作用中扮演着极为重要的角色,并且在光学测量、检测、显示和通信等[18-24]方面得到了广泛应用。但在这些应用中,采用的多为光束横向平面内各点偏振相同的标量光场,而在光束横截面上具有非均匀偏振分布的矢量光场,长期没有得到足够的关注和发展。2000年,BROWN T G 等在研究局部偏振方向沿径、角向偏振的柱矢量光场(即径向偏振和角向偏振光场)的聚焦特性时,发现径、角向偏振光场的紧聚焦可产生强纵向电、磁场[25-27]。首次揭示了光场偏振结构带来的独特光学特性,从而推动了人们对矢量光场研究的关注。随后,此类光场的超衍射极限聚焦等特性也逐渐被发掘。这些特性使得矢量光场在超分辨率成像和加工、显微操作和增强非线性效应等方面具有广阔的应用前景[28-38]。此外,矢量光场空间结构化的偏振态可作为光信息传输中模式复用或编码的另一个自由度[39-40]。因此,在过去的十年中,探索具有独特的传播和聚焦特性的新型矢量光场成为空间结构光场研究中的一个重要方向。
众所周知,光波是横波,即在自由空间中,电矢量垂直于传播方向。因此,偏振态和相位的调控主要致力于设计在横截面中具有不均匀分布的光场[41-58]。换句话说,偏振和相位的调制仅限于二维平面(即x-y平面)。然而,在光操纵和相关应用的需求下,新的空间自由度变得越来越重要,一些精心设计的具有特殊纵向变化的光场不断被提出。例如,以贝塞尔光束[5]和艾里光束[59]为代表的无衍射光束,在传输过程中能够维持电场分布不变且具有自愈效应;圆对称的艾里光束在传输过程中则表现出突然自动聚焦特性[60];振幅和相位通过衍射光学元件调制后的光场聚焦后,在轴向呈现出笼状、链状等[61-62]强度显著变化的特殊焦场等。
更多空间自由度上的调控进一步揭示了光的电磁性质。自从将拓扑结构引入到物理领域后,人们已经成功构建了在三维空间中,光涡旋和偏振矢量线、甚至电、磁场线呈现结、链等拓扑结构的新型光场。拓扑可以被认为是对其自身结构特性的探索,作为光子学中一种新的自由度,它不同于诸如幅度、相位和偏振等传统调制参数[63]。这种在实空间中具有拓扑结构的空间结构光场,在光操纵、光通信和量子信息传输方面具有广阔的应用前景[10,64-65]。此外,由于光学系统的可观测性,此类光场的调控也成为研究不同物质系统中常见拓扑性质的直观手段[63,66-68]。
综上所述,随着空间结构光场的深入研究和广泛应用,人们的目光逐渐由面内结构调控发展为三维空间的光场结构调控。在此情况下,首先需要拓展的便是光场纵向维度的调控。本文中,我们主要介绍在传播方向上对光场强度和偏振结构调控的研究进展。其中,第1 节介绍光场强度沿轴向的调控以及由此构建的特殊三维结构光场;第2 节介绍沿纵向具有特殊传输轨迹光场的两种构建方法;第3 节介绍绕光轴螺旋传输的光场,并分析了螺旋传输特性和调制机理;第4 节介绍光场偏振结构沿纵向的调控;第5 节介绍紧聚焦条件下光场强度和偏振结构的联合调控。
1 光场强度的纵向调控
光场强度纵向调控,本质上可以理解为光场沿传输方向的相干叠加控制。因而,可以通过引入两个或者多个光场分量,调控其沿传输方向的振幅和相位变化关系实现。通常采用的调控方法,主要借助傅里叶变换系统,即在频谱面对光场进行振幅和相位调控,由此引入离散的多个波矢分量或连续变化的波矢分量,依靠其传输特性在实空间引入纵向变化的相干叠加态,由此产生强度沿纵向变化的光场。
傍轴条件下,通过光场频谱调制控制纵向结构时,多采用频谱复振幅连续调控[69]。因而,这种方法能够实现更加灵活、丰富的纵向结构设计。众所周知,理想贝塞尔光场的频谱是一个环形的δ函数,即δ(kr-kr0)。其中,kr为贝塞尔光场的横向波矢分量。根据贝塞尔函数的正交性完备性,结构分布与角向无关的光场都可以看作一系列具有不同横向波矢贝塞尔频谱的叠加[70]。而具有不同横向波矢分量的贝塞尔频谱,其Gouy相移与纵向波矢分量呈线性关系[71],这为调控频谱分量之间纵向变化的相移提供了直接手段。例如,2004年,ZAMBONI-RACHED M 等[72]提出了光学“冻结波”的概念。这种纵向调制光场由一系列具有不同横向波矢分量的同阶贝塞尔光束同轴叠加而成。又由于任意贝塞尔函数的线性组合均可作为波动方程的解,因此光学“冻结波”也可以看做是波动方程在某一确定范围内能够稳定存在的一个新无衍射解[73,74]。其特征在于波包的群速度v=0,且光场强度的纵向结构可以任意调控。假设某一具有特定纵向分布的光学“冻结波”是由2N+1 个同频率的l阶贝塞尔光场同轴叠加而成,则其电场分量沿纵向的分布可以写为[75]


L是光场纵向调制的有效范围,Aj为每个贝塞尔函数所对应的权重因子,其大小由振幅纵向包络函数F(z)决定,即[70]

理想条件下,每一个贝塞尔函数的频谱可以写为δ(kr−kr0),则2N+1 个同轴同频率的贝塞尔光场的频谱由2N+1 个半径分别为krj的同心圆构成。根据傅里叶变换的线性定理,对于每一个贝塞尔函数Jl(kljρ)而言,其权重因子在傅里叶变换过程中保持不变,即频谱krj的系数仍为Aj,此时冻结波的频谱分布可以直接写为

式(4)右边即为光学“冻结波”的频谱,其取值范围由Q和L共同决定。图1 分别展示了基于频谱调制产生的零阶和一阶“冻结波”的光强沿纵向分布,即|Fl(ρ,φ,z,l=0)|2和|Fl(ρ,φ,z,l=1)|2,其光强沿纵向分布的包络分别用矩形函数和正弦函数表述。图1 左图上方的红线表示ρ=0 处归一化的光强随纵向分布,右图上方红线表示ρ=ρ0处归一化的光强随纵向分布,两图左边的红线表示在z=z0平面处的归一化光强分布。可以看出,0 阶冻结波的光强沿纵向虽然有一定波动,但总体分布符合光强纵向包络函数。由于正弦函数是亥姆霍兹方程的基本波函数,1 阶冻结波的光强纵向分布表现得更稳定、更平滑。

图1 光强纵向包络为矩形函数的零阶“冻结波”(左)和正弦函数的一阶“冻结波”(右)在ρ-z 面内的强度分布。红色曲线分别代表了径、纵向光强分布[75]Fig.1 Intensity distributions of Frozen waves with uniform(left)and sinusoidal(right)profiles along propagation direction.Lines:radial and longitudinal intensity profiles[75]
当考虑频谱函数连续分布时,并且同时只考虑轴上强度分布(ρ=0)时,可用零阶贝塞尔函数的汉克尔变换替代式(1),即

空间频谱可由轴上光强函数F(r=0,z)通过傅里叶变换得到,即

基于上述理论,本课题组[76]提出一种能够在轴向调控光场的超透镜。该器件借助了光学超表面在振幅和相位独立调控方面的优势,同时集成了频谱调制与傅里叶变换功能,因而具有集成化、小型化的特点。图2(a)为所设计的超表面结构扫描电镜图,图2(b)和2(c)为预设的沿纵向光强均匀分布的无衍射场所对应的理论计算及实验结果。图2(d)为实验测得的光强沿轴向变化的分布结果。图2(e)为实验测量的轴上光强分布。

图2 本课题组基于光学超表面实现的光场强度纵向调控[76]Fig.2 Longitudinal intensity modulation based on optical metasurface realized by our group[76]
2 轴向任意轨迹传输光场
自2007年艾里光束被实验证实以来[59,77],在过去的十几年中,对以艾里光束为代表的自加速光场的研究,不仅在基础理论和实验演示方面取得了长足的进步,还在广泛的应用方面取得了长足的进步。在空间傍轴和非傍轴条件下,研究者相继发现了不同类型的加速光场[78,79],同时也发展了丰富的方法来随意控制它们的轨迹、光束结构和宽度等。此类光场因其无衍射、自愈、自加速等特性,已被用于光束聚焦、粒子操纵、生物医学成像、等离子激元和材料加工等领域[80]。本文重点关注沿纵向具有任意轨迹的无衍射光场。
2.1 焦散线理论
控制光场的传输轨迹,除了寻找波动方程特异解,通常采用基于光学焦散线方法[81-86]设计的相位,通过对入射光的局部光线进行调控实现。根据焦散线理论,光波的传输轨迹可看作由初始平面各点源出射的光线在空间的交点,即光波轨迹切线的光线簇为焦散线。因此,在已知光波轨迹的前提下,可通过焦散线获得初始平面上点源(实空间位置)出射光线的方向(k空间位置),即相位变化关系。如图3(a)所示,以二维传输为例,当光场在x-y面内传输时,初始平面x=0 处的相位分布函数为φ(y),在此相位函数调制下光波的传播轨迹为f(x)。则可取曲线上任意一点(x′,y′),过该点做切线与y轴交于y0点,与x轴夹角为θ,满足关系

此切线即为从y0发出的光线。如图3(a)所示,借助式(7),通过红色焦散线便可得到调制光束主瓣沿不同弯曲轨迹传播的相位函数。图3(c)为根据该方法设计的沿抛物线和立方曲线传播的自加速光束传输过程对应的归一化强度分布。

图3 焦散线理论[88]Fig.3 Caustic principle[88]
上述方法只有在凸轨迹情况下,其一阶导数才为单值函数,与空间频率ky一一对应,进而求出对应的初始相位。对于非凸轨迹,WEN Y 等[87]提出了叠加焦散线的方法。其设计的思路是将非凸轨迹在所有拐点处断开成若干段凸轨迹,然后针对每一段凸轨迹采用焦散线方法得到其对应的初始场相位分布,通过组合相位进而实现这种沿非凸轨迹传播的自加速光束。在此基础上,利用坐标变量之间的可分离性,便可实现三维情况下沿任意轨迹的自加速光场。2017年,WEN Y 等[88]进一步提出了相空间设计自加速光束的方法。该方法将实空间和频谱空间结合,借助点光源与平面波的实空间和频谱空间特性,根据焦散线确定出构造自加速光束所需的光线簇。光线簇中每一个光线的出射位置及方向与相空间内一点(x,kx)对应,并由此获得魏格纳函数,进而得到所需的初始场分布和角谱分布。
2.2 沿任意轨迹传输的无衍射光场
1995年,ROSEN J 和YARIV A[89]提出使用傅里叶计算全息图来实现纵向形状可调控光束的产生,所需实现的曲线光束由一系列首尾相连的直线段近似表示,每一段直线由整个全息图中不同径向位置的环形子全息图再现。由傅里叶变换关系,当全息图的透过率函数附加一个适当的线性相位时,输出光束产生对应方向的横向偏移;而当透过率函数附加一个适当的二次相位时,输出光束则会产生纵向上的偏移;当透过率函数自身产生横向偏移时,输出光束则会围绕光轴产生旋转。因此对每个子全息图进行特殊的线性相位和二次相位相移,以及空间位移,便可产生所需的具有特殊传输轨迹的光场。
CHREMMOS I 等[90]进一步提出了一种产生沿任意轨迹传播无衍射光束的新方法。传统的锥形相位方法产生的贝塞尔光束沿光轴直线传播,可以看做由初始平面相同圆心但不同半径圆环发出的光线,在相同锥角(波矢条件)下汇聚而成的焦点轨迹。不同的是,该方法的相位调制函数由一系列移动圆心的扩展圆环构成,而传播的轨迹曲线是从输入平面上这些移动圆环发出的锥形光束汇聚而成,其原理如图4(a)所示。采用该方法,赵娟莹等[91]由预设轨迹反演设计二维相位调制函数,实现了遵循抛物线、蛇形、双曲线、双曲正割、甚至三维螺旋轨迹传输的无衍射自加速类贝塞尔光束。图4(b)和(c)给出了沿三维螺旋轨迹传输的自加速类贝塞尔光束的实验测量结果。这种光束的主瓣在传播过程中保持不变,甚至在受到扰动后可以自行恢复。对称的横向光束轮廓以及无衍射、自愈和轨迹可调性等特征使得这类光束在光学捕获和操纵等应用中展现了特别的吸引力[92]。此外,与基于焦散原理设计的光束相比,这种类贝塞尔光束可以遵循非凸轨迹传输,同时支持非傍轴条件下的大弯曲角度[93]和环状(高阶)模式[94]传输。
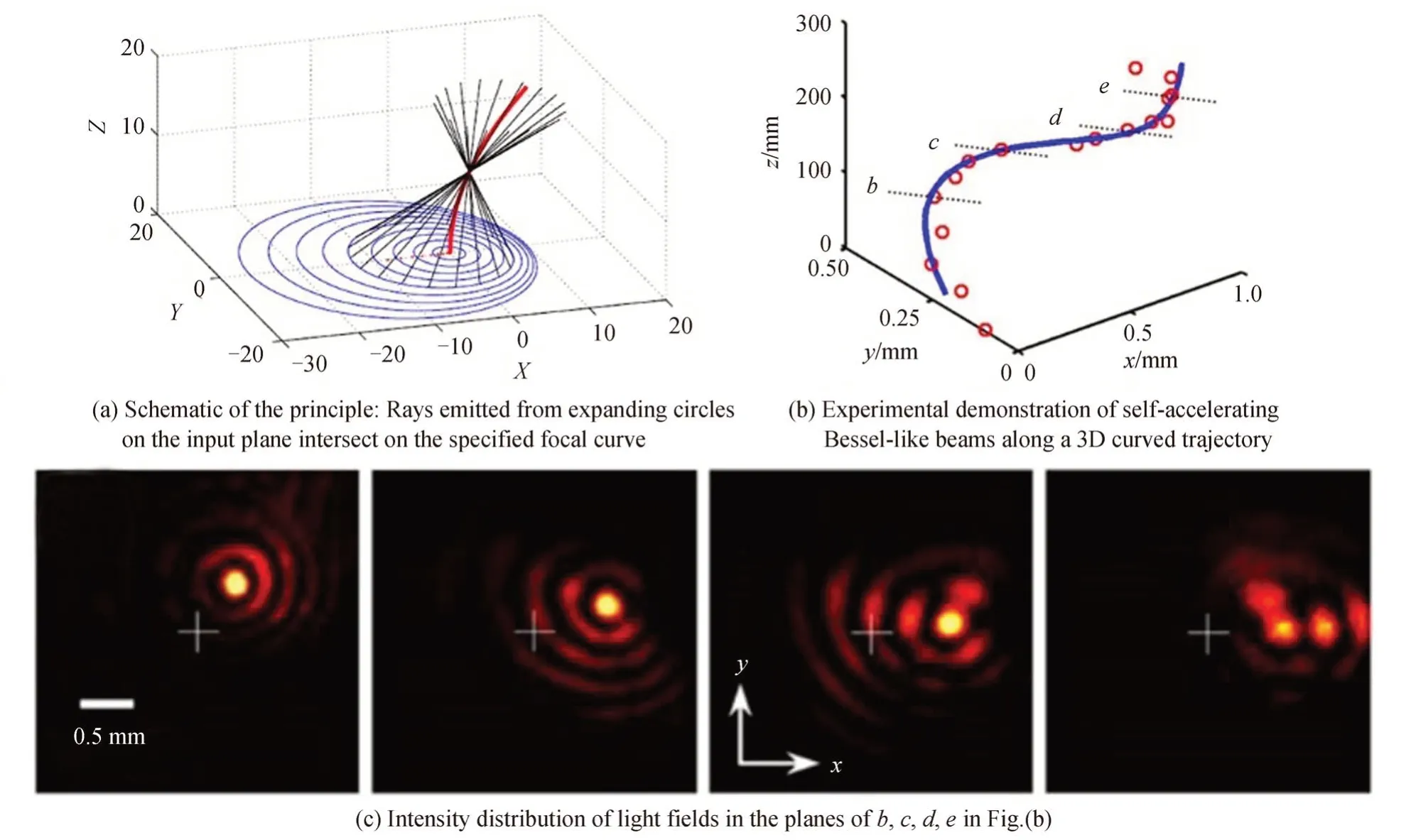
图4 任意轨迹自加速无衍射光场产生原理及产生的沿三维螺旋轨迹传输的自加速类贝塞尔光束[91]Fig.4 Schematic principle of rays emitted from expanding circles on the input plane intersect on the specified focal curve,and self-accelerating Bessel-like beams[91]
3 螺旋传输光场
3.1 等距螺旋传输光场
在任意自加速光场调控方面,沿传输方向具有等距和非等距螺旋轨迹的光场等[95-98]也因为具有新的自加速等特性而逐渐被开发,并发现其由于可形成特殊的点扩展函数而用于景深成像等方面。2014年,VETTER C 等[99]提出了一类新的自加速无衍射光场。如图5(a)所示,传统的艾里光束自加速传播过程中,其振幅和相位分布在与传输距离相对平移运动的参考系x′y′中不变。不同于此,研究者提出了一种如图5(b)所示的全新自加速光束。在传播过程中,这种光束在等距螺旋轨迹上不断演化,但同时在其旋转静止参考系x′y′中保持振幅和相位分布不变,这种光场也被称为径向自加速光场。这种特殊传播的光场可由亥姆霍兹方程的无衍射贝塞尔模式叠加构成。图5(c)显示了由0 阶和±1 阶贝塞尔光场同轴叠加而成的自加速光场。在传输过程中,无外部势场及非线性效应的情况下,能够保持光场轮廓并绕纵向轴螺旋传输,如图5(d)所示。由于径向自加速光束是非傍轴的,并且是全标量亥姆霍兹方程的解,因此可以在光学以外的许多线性波场中实现,如声波和弹性波、以及流体和软物质中的表面波等。

图5 艾里光束和径向自加速光场[99]Fig.5 Illustration showing the accelerative behavior of Airy and radially self-accelerating beams[99]

3.2 非等距螺旋传输光场
2015年,SCHULZE C 等[100]通过构建具有不同传播常数、且相位沿角向非线性变化的涡旋光场,实现了随传输旋转速度可调控的无衍射光场。众所周知,两个拓扑荷相反的涡旋光场(表示为e±ilφ,如图6(a)所示)同轴叠加后,呈现出沿角向为2l个花瓣状的光场,由于两个涡旋光场具有相同的传输特性,因此叠加场随传输距离不发生旋转。当两个光场具有不同的传播常数时,即Δkz=kz1−kz2≠0 时,两者存在随传输距离变化的相位差,可表示为φ(z)=zΔkz。因此花瓣状叠加场沿传输方向以Δkz/l的角速度匀速旋转,在一定衍射范围内也可作为一种径向自加速光场。当对旋转速度进行调控时,需要两个光场分量的相位差φ(z)对z的二阶导不为零。为此,研究者设计了相位沿角向非线性变化的特殊涡旋光场,其相位表示为Φ(φ)=lφ+αcos(lφ),如图6(b)所示。图6(c)所示为这种特殊涡旋与传统涡旋沿角向相位变化对比结果。同时为了保证叠加场轮廓不随光场传输而变化,引入了无衍射光场,所产生的叠加场表示为
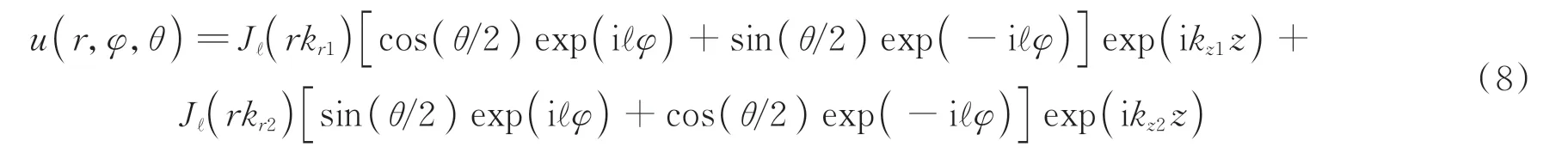
式中,Jl(·)表示第一类l阶贝塞尔函数,θ为常数,决定两个光场分量的非线性相位结构,同时也决定了其相位差沿z方向的变化率。此时,叠加场的旋转角速度为

角加速度为

图6(d)是两个具有相反的非线性涡旋相位的贝塞尔光场、及其叠加场的强度和相位分布。图6(e)和6(f)分别为θ=0、l=1 和θ=π/3、l=3 情况下的数值计算和实验结果。可以看出,光场的旋转角速度随传输不断变化,先增大再减小,在特定位置处,呈现出急剧增大的角速度。还可看出,通过控制拓扑荷,也可实现旋转角速度的调控。

图6 非线性涡旋光束叠加产生的非等距螺旋传输光场[100]Fig.6 Spirally propagating light fields with non-equidistant period produced by the superposition of nonlinear vortex beams[100]
3.3 径向结构调制的螺旋传输光场和分段调控的螺旋传输光场
2017年,WEBSTER J 等[101]利用两个拓扑荷相反且瑞利长度不同的径向高阶拉盖尔-高斯光束,在焦平面附近产生了纵向相关的自加速花瓣状螺旋光束,如图7(a)所示。这种光束在传输过程中,其外环和内环的光场结构旋转方向相反,且当外环旋转加速时,内环部分减速,总轨道角动量守恒。图7(b)呈现了角、径向阶数分别为l=2 和p=2 情况下的扭结光束的旋转传播特性。2021年,邓铎等[102]利用两个具有不同传播常数的同轴贝塞尔光束聚焦产生了完美旋转光束,其具有半径大小可控的完美涡旋特性,以及沿传输方向可控的旋转速度,如图7(c)所示。除了强度结构特性外,其旋转可控性使得这类光场可用于遥感测量光程、温度和折射率等方面。
与这种连续旋转不同,DORRAH A H 等[103]借助光学“冻结波”的方法,实现了旋转结构沿轴向的分段灵活调控。如图7(d)所示,该光场在5 ≤z≤35 cm 范围内,由具有不同传播常数且涡旋相位拓扑荷分别为l1=−2 和l2=2 的光学“冻结波”构成,由于贝塞尔光场的线性传播特性,因此“四瓣”状光场随传播呈现出匀速旋转。在35 ≤z≤75 cm 范围内,两光学“冻结波”的涡旋相位拓扑荷变换为l1=2 和l2=−2,因此“四瓣”状光场随传播呈现出相反方向的匀速旋转。在75 ≤z≤95 cm 范围内,由于两光学“冻结波”涡旋相位再次翻转,其旋转方向亦随之变化。图7(e)显示了该光场沿轴向的旋转方向和角速度分布。进一步,该课题组将这种纵向结构轨道角动量可控的光束用于测量介质折射率。其测量灵敏度可以超过~2 700°/RI,分辨率为~10-5RIU[104]。

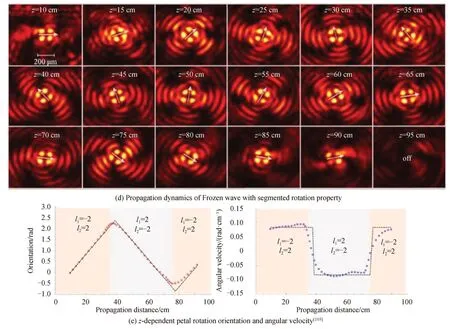
图7 旋转特性沿径向和纵向调控的螺旋传输光场Fig.7 Spirally propagating light fields with radially and longitudinally modulated rotations
4 光场偏振态的纵向调控
近年来,除了面内偏振结构调控,在传播方向上的光场偏振结构调控也逐渐引起关注,特别是一些由不同本征模式相干叠加而成的矢量光场,其强度、相位和偏振结构在光场传播过程中均会发生变化。获得此类光场结构的演化规律以及调控这种传输演化的方法,有助于开发出更多的潜在应用。根据沿纵向偏振态变化过程中,光场结构(模式)是否发生明显变化,又可将偏振态纵向调控定义为广义和狭义两种。
4.1 广义的光场偏振态纵向调控
无论是采用正交偏振模式相干叠加,还是偏振转换元件产生矢量光场时,偏振调制机理都可通过将入射光场分解为左、右旋圆偏振分量进行理解。假设入射的标量光场Ein,左、右旋圆偏振态(自旋态)分别为EL,ReL,R,其中EL,R为入射光场两个自旋态的复振幅分布,表示左、右旋偏振态的单位矢量。经过偏振调制系统后,出射光场为Eout=M·Ein=ELei2φeR+ERe-i2φeL。在偏振转换过程中,两个自旋态对该偏振转换系统有不同的响应,分别获得相位2φ(x,y)和−2φ(x,y)。该相位是一种典型的几何相位,也称为Pancharatnam-Berry(PB)相位。利用PB 相位不仅可以对光场的两个自旋分量进行波前整形,也可通过其对两个自旋分量的传输进行调控。
当选择的PB 为平面波相位时,即2φ(x,y)=kxx,其中kx表示平面波沿x方向的波矢分量。入射的标量光场通过该系统后形成的左、右旋圆偏振分量分别获得倾斜相位kxx和−kxx,在此相位调制作用下,两者在传输过程中发生横向分离,即光自旋霍尔效应[105]。2002年,HASMAN E 等[106]提出了空间变化的亚波长光栅,并发现了这种光栅的偏振选择性,即不同圆偏振光束经过该光栅会朝不同方向衍射。2013年,ZHANG X 等[107]利用光学超表面实现了这种增强的光自旋霍尔效应。所采用的超表面由横向周期变化的V 型金纳米天线构成,入射到该材料上的线偏振光束,其自旋分量会获得相反的横向相位梯度,发生横向分离。2015年,罗海陆等[108]利用飞秒激光在玻璃上诱导出的周期性弯曲纳米光栅实现了显著增强的光自旋霍尔效应。若将入射光场选择为具有涡旋、厄米-高斯、艾里光场,甚至任意强度分布的光场,则在出射光场都能分裂为复振幅分布完全相同、偏振态分别为左、右旋圆偏振态的两束光[109]。
当选择的PB 相位为二次相位时,即2φ(x,y)=αr2,其中α为控制光场发散和会聚的常数。若令光束的左、右旋自旋分量分别获得(乘以)相位因子exp(iαr2)和exp(−iαr2),即左旋分量发散(α>0),而右旋分量会聚在f(α)=k/2[α+(αw4)-1]处,其中k为波矢大小(波数),w为入射光斑半径,则两个分量将形成自旋相关聚焦。2003年,HASMAN E 等[110]利用径向变化的纳米光栅,实现了焦距为±f的偏振相关的双焦距透镜。2014年,崔一平等[111]发现了这种径向偏振变化光场的双聚焦现象。2016年,本课题组[105]利用塞纳克干涉仪对光束偏振态的转换特性进行了调控,通过调控PB 相位不仅实现了对两个自旋态横、纵向分离,还可通过两者的结合实现了自旋态三维空间分离的任意调控。例如,将PB 相位设置为2φ(x,y)=kxx+kyy+αr2时,两个自旋态经过偏振转换系统后,将分别聚焦在坐标(xR,yR,zR)和(xL,yL,zL)处,其中zR,L=f(α0±α),xR,L=kxzR,L/k,yR,L=kyzR,L/k,如图8(a)~8(c)所示。此外,PB 相位还可以携带螺旋相位,由此产生自旋相关分离的OAM 光场。图8(d)和8(e)为自旋相关的OAM 分离实验结果。
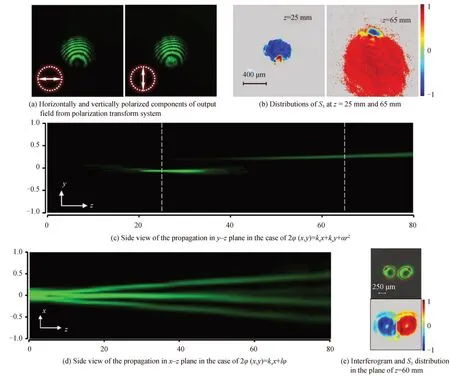
图8 PB 相位调控下光场传输过程中的偏振结构变化[105]Fig.8 Evolutions of polarization distribution of light fields with the modulation of PB phases[105]
罗海陆等[112]利用这种自旋相关聚散焦效应,提出了一种光子自旋滤波器。该滤波器由两个共焦的超透镜构成。入射光场在第一个透镜作用下,两个自旋态分别产生会聚和发散行为,在频谱面利用一个小孔进行低通滤波,可过滤掉发散的自旋态,再通过第二个超透镜将自旋态还原。张岩等[113]利用超表面实现了自旋相关聚焦分离,并进一步利用其实现了偏振选择成像。
4.2 狭义的光场偏振态纵向调控
上述的光场在传播过程中,由于自旋分离,光场的偏振分布随传输距离发生变化。值得注意的是,在此过程中,光场的强度分布结构也发生了明显的变化。如果可以产生具有稳定模式特性且偏振态纵向连续变化的特殊光场[114-127],必然可以进一步拓展矢量光场的应用领域。例如,这种特殊光场可以改变具有偏振依赖特性介质中不同纵向位置处的吸收峰值,激发其非线性折射率分布等。
2013年,CARDANO F 等[128]利用正交偏振的高斯光束和拉盖尔-高斯光束同轴叠加,得到了庞加莱光束。由于两个模式参量具有不同的模式特性,其Gouy 相移差随传输距离变化。在瑞利距离内,随着光传播,叠加后的庞加莱光场偏振结构随之旋转,表现为Lemon、Star、Spiral 型拓扑结构的空间旋转。但由于Gouy 相移变化缓慢,从−ZR到ZR,偏振结构旋转了π/2。2015年,MORENO I 等[129]利用贝塞尔光束产生了偏振结构随着传输线性旋转的偏振态纵向调控无衍射光场。利用锥形双折射棱镜提供沿径向变化的相位延迟,实现径向变化的偏振态;然后,利用锥透镜生成贝塞尔光束时的横-纵向映射关系,实现了不同传输距离处偏振态的控制,即偏振态纵向调控的标量无衍射光场。进一步,在通过偏振转换系统和锥透镜的组合,为两个自旋分量引入不同斜率的径向线性变化相位(可作为PB 相位),产生了偏振态和偏振阶数随传输距离变化的矢量贝塞尔光束[130]。
2016年,本课题[131]组利用频谱调制方法调控两个正交偏振分量的纵向振幅关系,提出了一种偏振态纵向调控的无衍射光场,其偏振态随传输可沿庞加莱球上任意轨迹变化。根据偏振态的庞加莱球表示方法,庞加莱球上的每一个点(2φ,2χ)都对应一个确定的偏振态,而这个偏振态可以分解为任意两个关于球心对称的正交偏振分量。也就是说,同轴叠加两个具有任意振幅比和相位差的正交偏振分量可以得到庞加莱球上任意一点的偏振态。为了构造偏振态纵向变化的无衍射光场,假设两个正交偏振分量分别为水平和竖直线偏振,且强度分布符合贝塞尔函数。则矢量光场的电场强度分布可以表示为
式中,EH,V(z)分别表示水平和竖直偏振分量的归一化纵向振幅包络函数,δH,V(z)表示相位延迟。根据琼斯矢量和偏振椭圆之间的关系,可以将上述偏振态用椭圆率角χ以及方位角φ来表示为
式(12)表明,通过两种方法实现偏振态的纵向连续变化:1)调控两个偏振分量的轴上振幅比,即纵向强度包络函数,使其满足EH(z)/EV(z)≠const;2)调控两个偏振分量的相位差,使其满足δH(z)−δV(z)≠const。
图9 是根据式(12)分别通过调制纵向振幅和相位包络实现的偏振态纵向调控无衍射光场。其中,图9(a)为频谱调制光场轴向振幅包络的示意图,其调制原理由对应的频谱变换关系式(5)和(6)得到。如图所示,当对入射光场的两个正交偏振分量在频谱空间进行复振幅独立调控,可在实空间获得沿轴向线性增强或减弱的光强包络。由于采用贝塞尔频谱,叠加场同样具有无衍射特性。图9(b)为实验测得的两个偏振分量的光强随传输变化情况。图9(c)为这种强度包络情况下,光场的斯托克斯参量S3(椭圆率角)随传输的变化情况。因为两个正交分量的振幅比非线性变化,导致偏振态非线性变化,同时也反映了这种方法可以灵活调控偏振态变化。此外,通过调控PB 相位,获得了偏振态沿纵向自动变换的高阶矢量贝塞尔光场,如图9(d)所示。这种三维变化的偏振态,同时也具有自愈特性。如图9(e)所示,这种纵向变化的偏振特性经过障碍物后表现出了良好的自愈能力[132]。
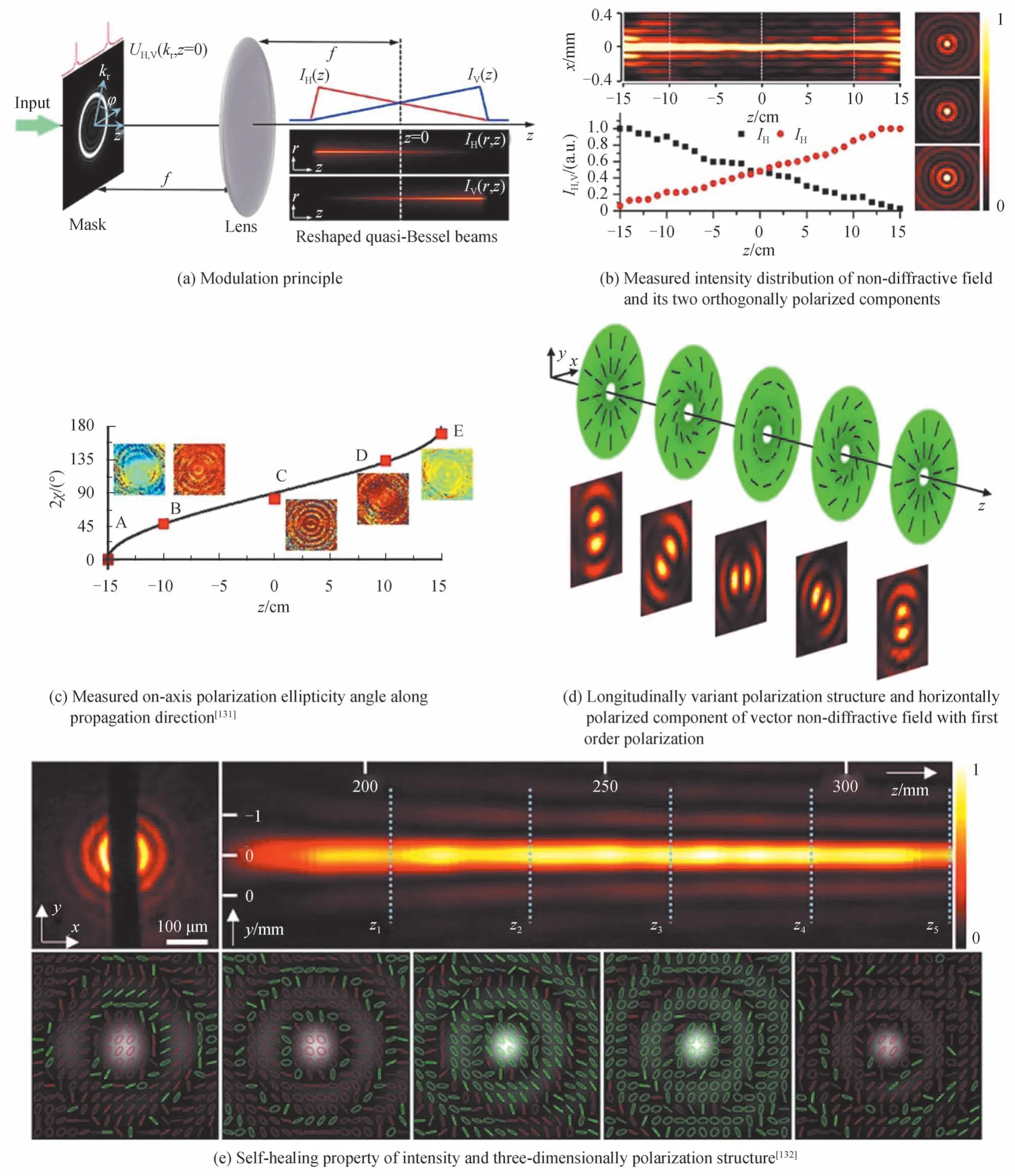
图9 无衍射光场的偏振结构纵向调控Fig.9 Longitudinally manipulating the polarization structures of non-diffractive beams
2020年,利用径向高阶拉盖尔-高斯模式与贝塞尔模式的Gouy 相移特性,进一步实现了偏振态沿纵向的非线性变换[133]。我们发现,径向高阶拉盖尔-高斯光场不仅具有与同阶贝塞尔光场高度相似的模场分布,更具有类贝塞尔光场的无衍射特性,这为保证光场模式的传输稳定性提供了基础。此外,拉盖尔-高斯光场具有与贝塞尔光场显著差异的Gouy 相移,表示为ΦLG=(2p+|l|+1)arctan(z/ZR)。当采用径向阶数较大的拉盖尔-高斯光场时,Gouy 相移随着传播距离的增加非线性累积,且随着角向阶数的不断增大,非线性累积过程加剧,即可通过调控偏振阶数、径向阶数等参量控制非线性变化率。
5 紧聚焦下的光场强度和偏振态纵向联合调控
透镜作为最常用的二维傅里叶变换系统,在其焦平面附近的光场纵向调控得到了广泛研究。采用大数值孔径的物镜进行紧聚焦成为了最常用的实验模型,不仅为引入较大的纵向相位变化率提供了可能,还可以通过紧聚焦下的偏振转换诱导强的纵向场分量[25,134],因此围绕紧聚焦场强度和偏振态的纵向以及三维结构调控开展了广泛研究[135-160]。2005年,赵逸琼等[135]率先开展了焦场纵向调控研究,主要是通过环状衍射光学元件(Diffraction Optical Element,DOE)对入射径向偏振光场的相位进行调制。如图10(a)所示,DOE 具有三个同心圆环,其透过率分别为T1=exp(jφ1)、T2=0、T3=exp(jφ3),每个区域外环相对交点的张角分别为0.4θ、0.9θ和θ。其中,θ由透镜的数值孔径NA 决定,即NA=sinθ。用该DOE 调制入射径向偏振光场的相位时,由于DOE 两透光环产生的聚焦场之间的Gouy 相移在焦平面附近随传输距离显著变化,因而可以形成振幅/强度沿光轴显著变化的相干场。同时,由于紧聚焦,焦场在横向平面内同样具有较快的相位变化,因此其强度的三维分布沿轴向呈现出准周期的链状结构,这种特殊的焦场也被称为“光链”,如图10(b)和10(d)所示。通过调控两透光环的相位差,即Δφ=φ1-φ3,可以实现“光链”的移动及方向控制。同时,这种中空状的结构特别适合用于粒子捕获,并且当将粒子捕获在该链状结构中时,还可以通过控制相位差实现捕获粒子的定向输送。

图10 二元相位和振幅调制下径向矢量光场的紧聚焦场Fig.10 Tightly focusing fields of radially polarized light fields with radial binary phase and amplitude modulation
随后,KOZAWA Y 等[136]利用径向高阶(TEM11模式)的柱矢量光场,在紧聚焦条件下,当光瞳与光束半径比为1.3 时,由于相消干涉导致纵向分量在焦点处消失,产生了一个纵向长度为波长量级的暗区,该暗区的形状如图10(c)和10(e)所示,这种光场也被称为“光笼”。2009年,汪喜林等[137]利用双模柱矢量光束紧聚焦,实现了可控“光笼”的产生。如图11(a)所示,通过调控入射双模柱矢量光束的局部偏振方向,可实现“光笼”形状的改变。当内、外环偏振方向为φ1=0.089π 和φ2=0.791π 时,径向分量峰值强度为纵向分量的一半;当φ1=0.089π、φ2=0.632π 时,纵向分量峰值强度为径向分量的一半,如图11(b)和11(c)所示。2015年,聂仲泉等[138]引入图11(d)所示的双环涡旋DOE,对角向偏振贝塞尔-高斯光束进行调控,在高数值孔径聚焦情况下,通过调整DOE 每个环的半径,可以在焦点区域同时生成纯横向偏振“光链”,以及具有单通道的亚衍射极限(横向宽度0.518λ)的纯纵向“磁链”(纵向长度12λ),如图11(e)所示。进一步,利用级联的DOE,可以产生周期瓶状的磁通道,以及具有双通道的纵向磁链(纵向长度12λ)。这类中空结构的可调控焦场,在粒子捕获及定向输运方面[139-140]展现了极大的应用价值。此外,“光笼”和“光瓶”类中空结构焦场,还在荧光受激损耗显微术等方面,具有极大的应用潜力。

图11 利用偏振和相位调控的柱矢量光场紧聚焦产生光笼和光链Fig.11 Generation of light′cage′and light′chain′based on the tight focusing of cylindirally polarized beams with modulated polarization and phase
相比于单个透镜,双透镜4π 聚焦为相干叠加提供了更丰富的光场模式。例如,2012年,陈子阳等[141]利用径向偏振涡旋光场的4π 聚焦,在紧聚焦条件下,通过调控入射光场径向透过率,以及两个反向聚焦光场的偏振模式,实现了具有特殊纵向强度分布的焦场。当采用具有相反偏振方向的1 阶径向偏振拉盖尔-高斯光束聚焦时,产生了中空尺寸为0.32λ(横向)和0.34λ(纵向)的球状焦场;当采用具有相反偏振方向的2 阶径向偏振拉盖尔-高斯光束入射时,产生的中空光束暗通道能够长达30λ。此外,詹其文等[142]系统研究了4π 聚焦情况下,轴向具有均匀强度的多焦点阵列形成机制,建立了用于构建此类焦场所需的入瞳面光场结构反演机制。
与上述情况相反,轴向具有均匀强度的焦场,在超分辨成像、微加工等技术领域具有重要应用价值。因此,如何抑制轴向结构变化,构建强度均匀的超长“光针”型光场[143-159],长期以来一直是焦场纵向调控的重点。2008年,WANG H 等[160]率先通过相位调制的DOE,在紧聚焦条件下,利用径向偏振的贝塞尔-高斯光束入射,产生了一个纵向长度约为4λ,横向半高全宽约为0.43λ的无衍射“光针”。所采用的聚焦模型及DOE透过率函数如图12(a)和12(b)所示,该DOE 具有五个不同宽度的环形孔,其对应的归一化外径为r1=0.091,r2=0.391,r3=0.592,r4=0.768,振幅透过率均为1,相邻两环之间的相位延迟为π。采用该DOE 调制径向偏振光场,不仅能够有效抑制紧聚焦场在焦平面附近的发散行为,更能够将焦场的偏振态接近完全转化为纵向分量。焦平面附近的各偏振分量强度分布及总光强分布如图12(c)所示。随后,如何构建具有超衍射极限、超长的“光针”被广泛研究。
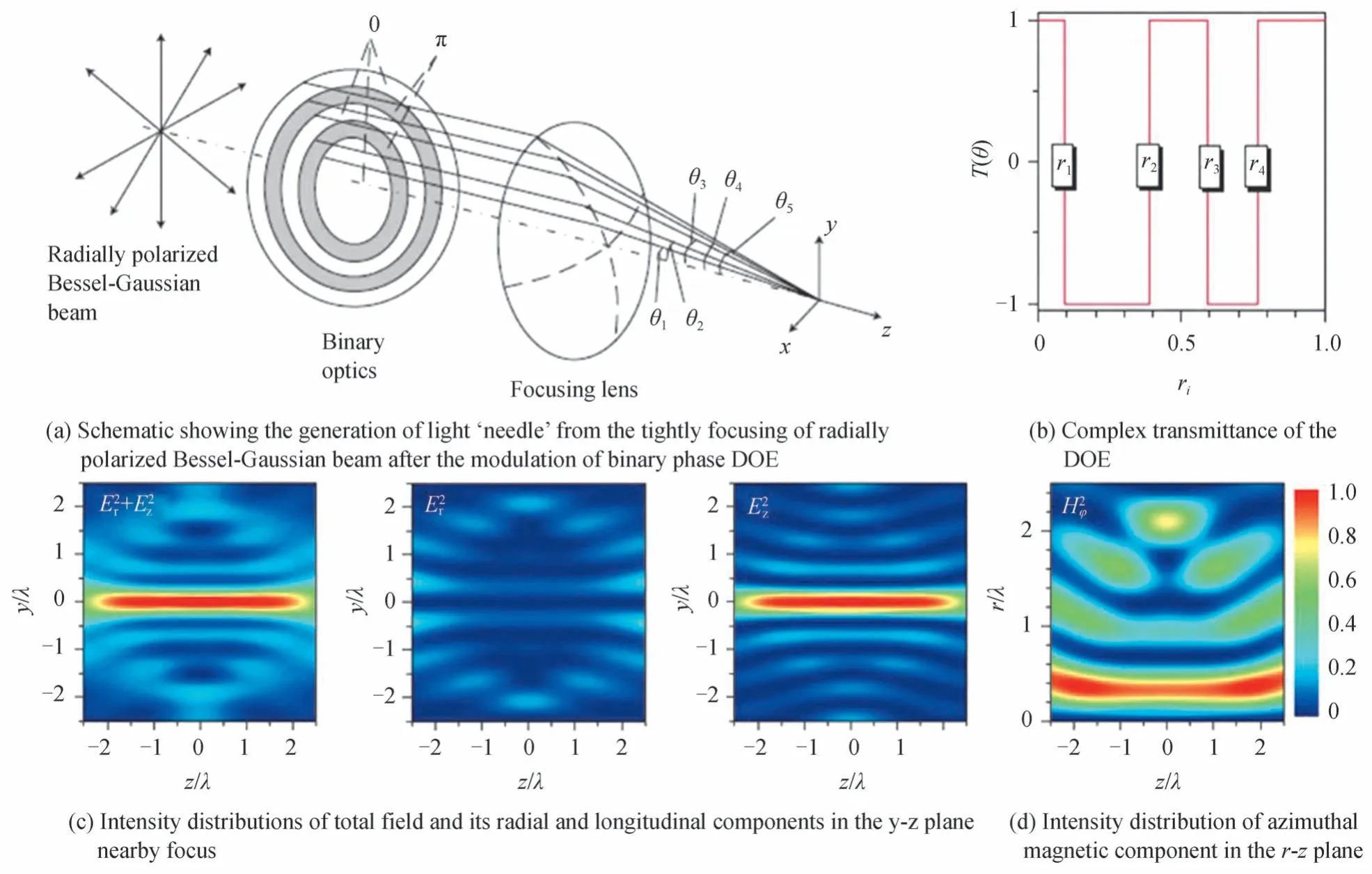
图12 聚焦径向偏振贝塞尔-高斯光束产生光针[160]Fig.12 Generation of light′needle′from the tightly focusing of radially polarized Bessel-Gaussian beam[160]
6 总结与展望
得益于特殊的空间结构,振幅、相位、偏振调控的光场在传输及与物质相互作用过程中展现了一系列引人瞩目的新效应和新现象。诸多面内调控光场,已经成功用于超分辨成像、微粒操控、激光微加工、信息传输与修复等方面,并且在生物医学、信息科学、量子光学、计量学中展现出重要的应用前景,所形成的面内调控理论也已成功推广到其它相关体系。在此过程中,光场沿传播方向的调控原理、方法和器件也在不断发展。控制光场沿传输方向的变化,为进一步发展调控光场在光学微操纵、显微成像、光学加工、角动量控制、信息存储以及三维结构光子态调控等方面的应用提供了更充足的手段。
然而,光场纵向调控还有诸多不足。如现有的纵向调控方法,多数基于光场的相干叠加原理。而这种相干叠加依赖于现有的光场横向调控,即亥姆霍兹方程傍轴近似条件下得到的横向模式。一方面,这种叠加态在传输过程中由于空间模式色散等问题,导致难以长距离传输;另一方面,纵向调制受限于传输条件,周期通常较大。因此需要从波动方程构建三维空间关联的本征模式,如涡旋拓扑结构光场[161]等,不仅有助于拓展调控自由度,还可实现纵向周期压缩等,拓展新模式在提高显微纵向分辨率等方面的应用。此外,随着光场纵向调控技术的发展,也亟需集成的相关调控器件的发展,特别是不依赖于入射光场偏振等特性的新型光学器件[117],这将会激发更广泛、更深入的理论和应用探索。
