大地电磁二维DCG、NLCG和L-BFGS反演算法对比
2022-02-21吴桂桔谈洪波
李 磊,吴桂桔,谈洪波
(中国地震局地震研究所 地震大地测量重点实验室,湖北 武汉 430071)
1 引 言
大地电磁法(Magnetotelluric,MT)作为地下深部结构探测的一种重要手段,已经被广泛地应用于地壳和上地幔的电性结构探测工作[1,2]。目前,在所有地球物理方法中,MT是除地震方法以外探测壳幔结构最重要的方法,这是因为它不仅成本低,便于实际野外施工,而且分辨能力高,探测深度大。由于真实地下介质的电性结构常具有三维性特征,为了反演结果的真实性,MT野外实际采集资料最好采用三维反演方法[3,4]。虽然一些复杂的区域可能需要三维反演,但三维反演计算需要耗费大量的时间,二维反演的计算时间更快(肖俊等,2020)[5]。一维反演可以作为二维或三维反演的初始模型(刘嘉文等,2018)[6]。此外,二维反演可以方便地加入地形的影响,这是一维反演所不具备的(岳明鑫等,2019)[7]。因此,MT二维反演仍是目前最主流的处理手段。
MT二维反演方法种类很多[8-13],常用的方法包括Occam反演法[14-16],快速松弛反演法(RRI)[17], 非线性共轭梯度法(NLCG)[18],数据空间Occam反演法(REBOCC)[19]以及数据空间共轭梯度法(DCG)[20]等。这些方法都属于基于目标函数梯度信息的最优化迭代反演方法,但它们具有不同的特点,有的单次迭代计算速度快、内存需求小,有的迭代收敛速度快。从理论上来看,在目标函数中的模型约束项、数据拟合项采用统一定义的情况下,这些不同反演算法的结果应该是基本一致的(在收敛条件也相同的情况下)。然而,实际情况却并非如此,由于实际野外地质结构的复杂性[21],实测MT资料使用不同的反演方法往往效果相差明显。因此在实际应用中,MT资料处理工作者都要面临着如何选取更适合的反演方法的问题。
本文将对DCG、NLCG以及有限内存拟牛顿法(L-BFGS)[22]三种二维大地电磁反演方法进行对比。虽然之前也有学者对MT二维反演算法进行过对比[23],但对比的主要是Occam和数据空间Occam类方法,没有对DCG和L-BFGS对比过。本文首先介绍这几种方法的基本理论,然后设计典型的地电模型,使用以上三种反演算法对这些模型进行反演试算。本文使用TE、TM、Tzy三种不同模式下的数据进行反演,同时对比不同反演算法的效果,以期得出不同反演方法对反演结果以及对地球物理解释工作的影响,从而方便地球物理工作者在实际进行大地电磁处理解释工作时更好地选取MT二维反演方法。
2 大地电磁常用反演算法的基本理论
2.1 目标函数
DCG、NLCG和 LBFGS三种MT二维反演方法都属于正则化反演方法,它们的目标函数可表示为:
φ=φd+αφm
(1)
式(1)中,φ是总目标函数;φm为模型约束目标函数;φd是观测数据目标函数;α是正则化因子;m表示模型向量,d表述数据向量。
常用的模型约束函数有下列三种:
1)最小模型约束目标函数,模型参数平方和达到最小值:
φm=‖m‖2=(m,m)min
(2)
2)最平缓模型约束目标函数,模型参数的一阶导的平方和达到最小值[2]:
φm=‖∇m‖2=(∇m,∇m)min
(3)
3)最光滑模型约束目标函数,模型参数的二阶导的平方和达到最小值:
φm=‖∇2m‖2=(∇2m,∇2m)min
(4)
2.2 数据空间的共轭梯度法(DCG)
DCG就是用共轭梯度法(CG)在数据空间来求解反演法方程,被称为数据空间共轭梯度法[4],所以先给出共轭梯度法的基本公式。
2.2.1 共轭梯度法(CG)
CG迭代过程:
(5)
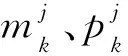
(6)
搜索方向可以表达为:
(7)
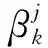
(8)
(9)
Cd是数据协方差矩阵,Cm是模型协方差矩阵。所以梯度向量迭代方式可以改写成:
(10)
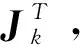
2.2.2 基于数据空间的共轭梯度法(DCG)
将上述CG算法引入到数据空间反演方法中,经过推导可得到基于数据空间的共轭梯度反演算法(DCG)。把模型更新迭代当作是解方程Ax=B,把求解方程转换为求f(x)最小值,表示为:
(11)
把数据空间的反演模型迭代形式进行分解:
(12)
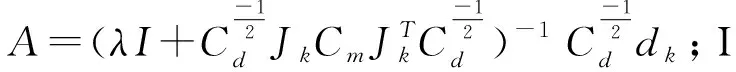
运用共轭梯度算法求解上式方程组,以下为DCG反演计算流程;
1)选择较好的mprior和初始模型m0;
2)外层循环:n=0,1,2…….,计算dn=d-F(mn)+J(mn-mprior)。F(mn)为当前迭代中的模型响应;
4)设x0=0,r0=p0=dn;
5)内循环(共轭梯度迭代);
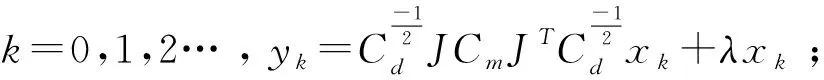
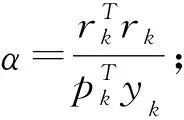
8)xk+1=xk+αkpk;
9)rk+1=rk-αkyk;
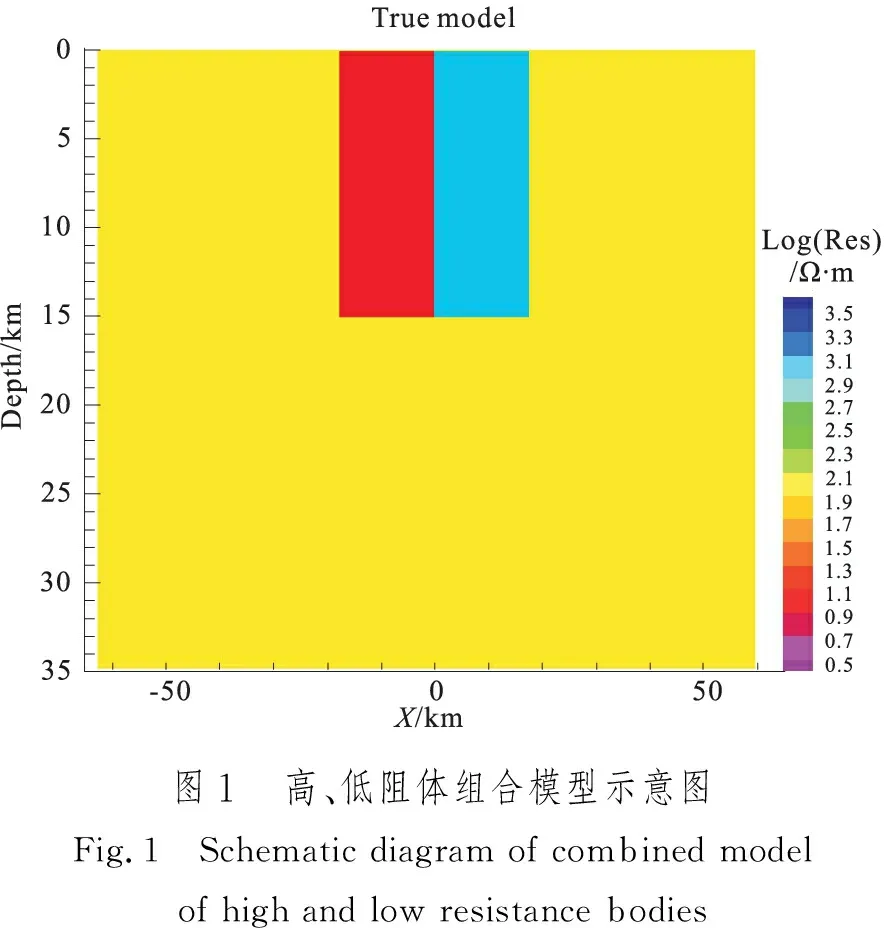
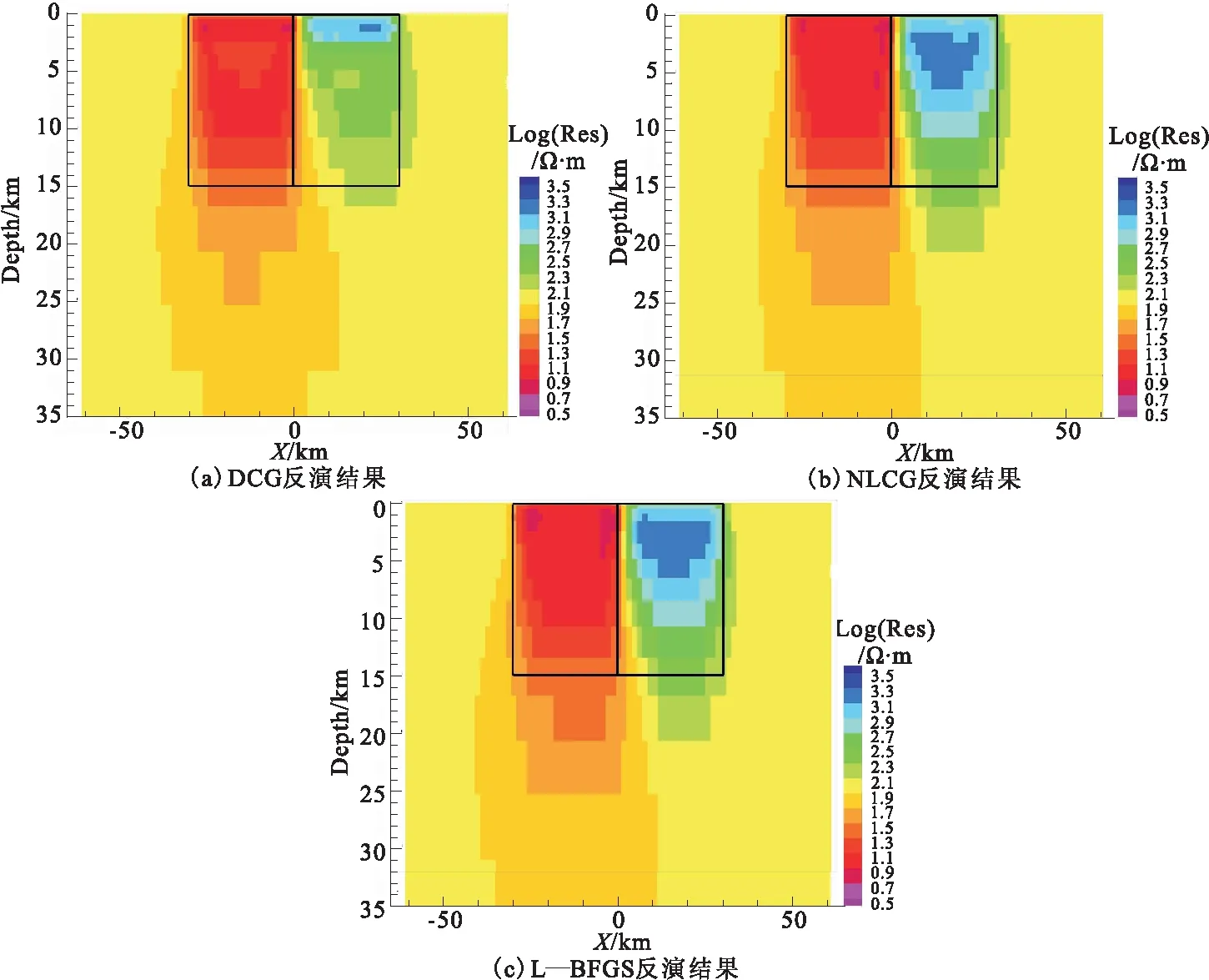
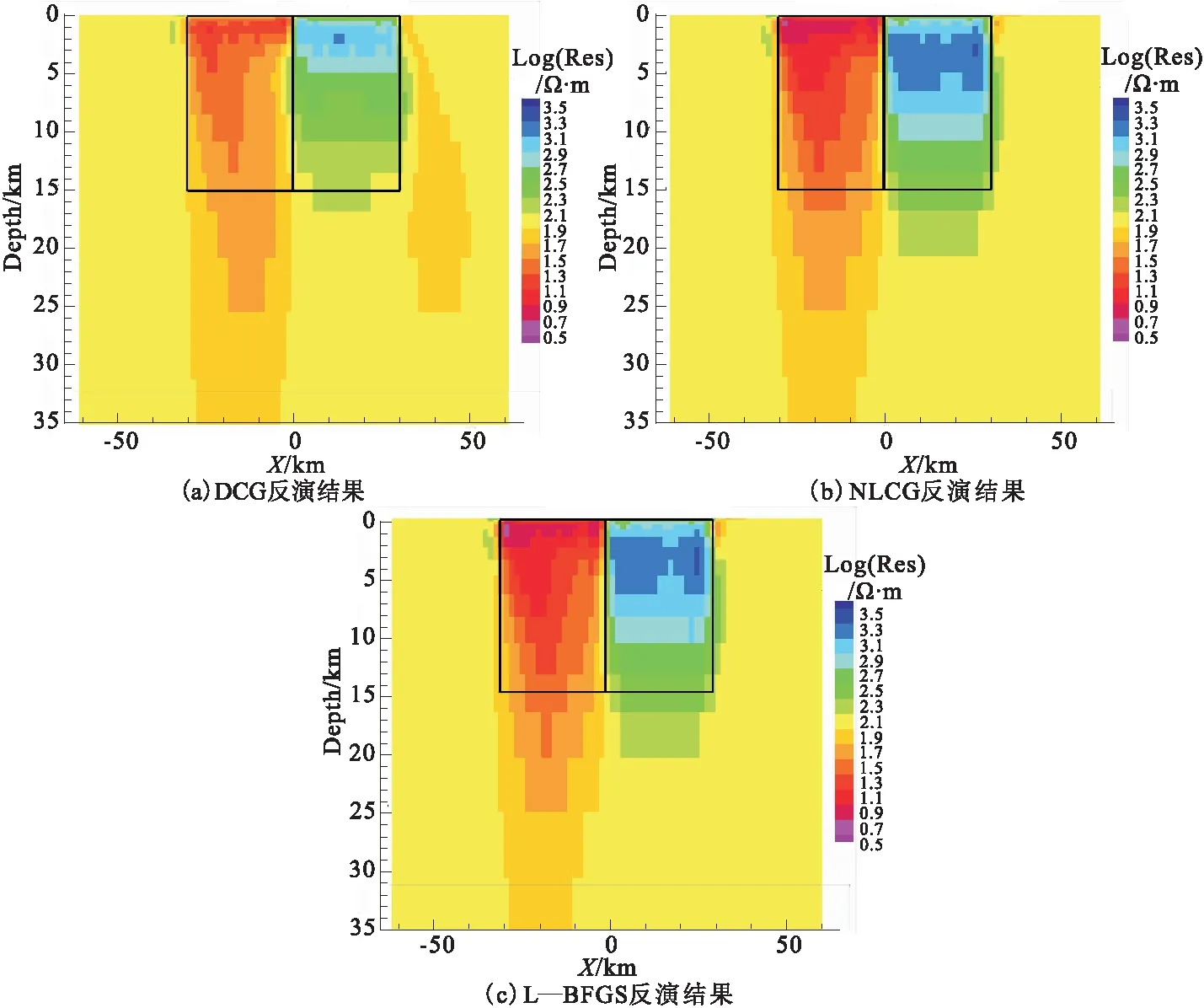
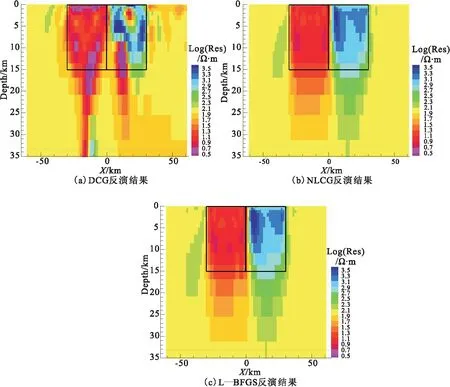
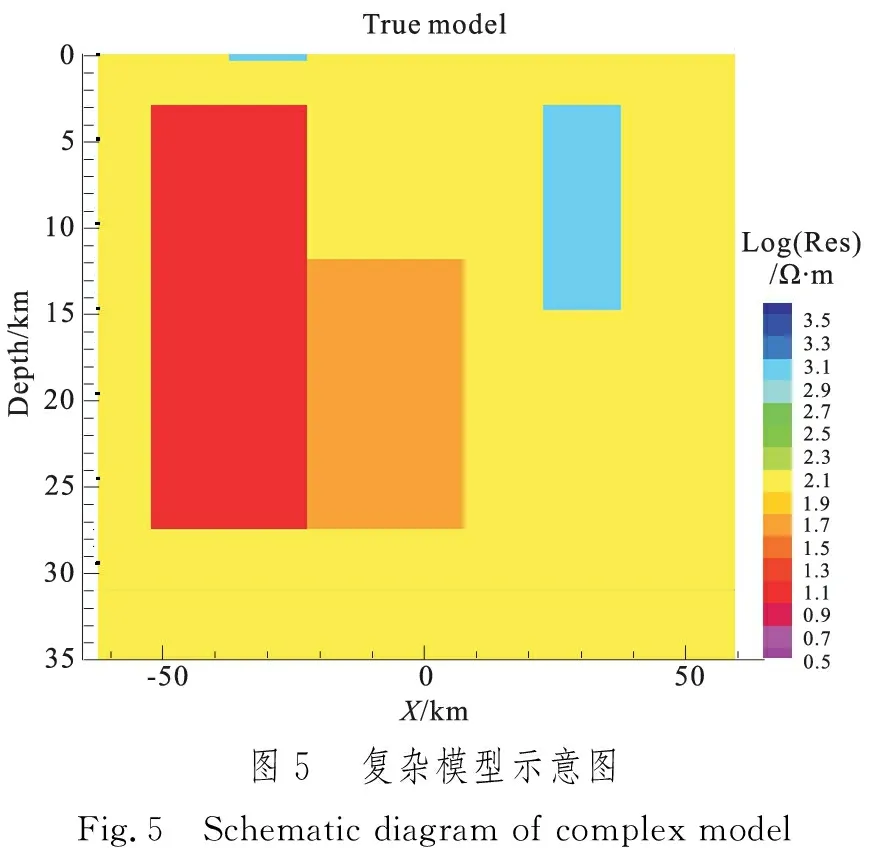
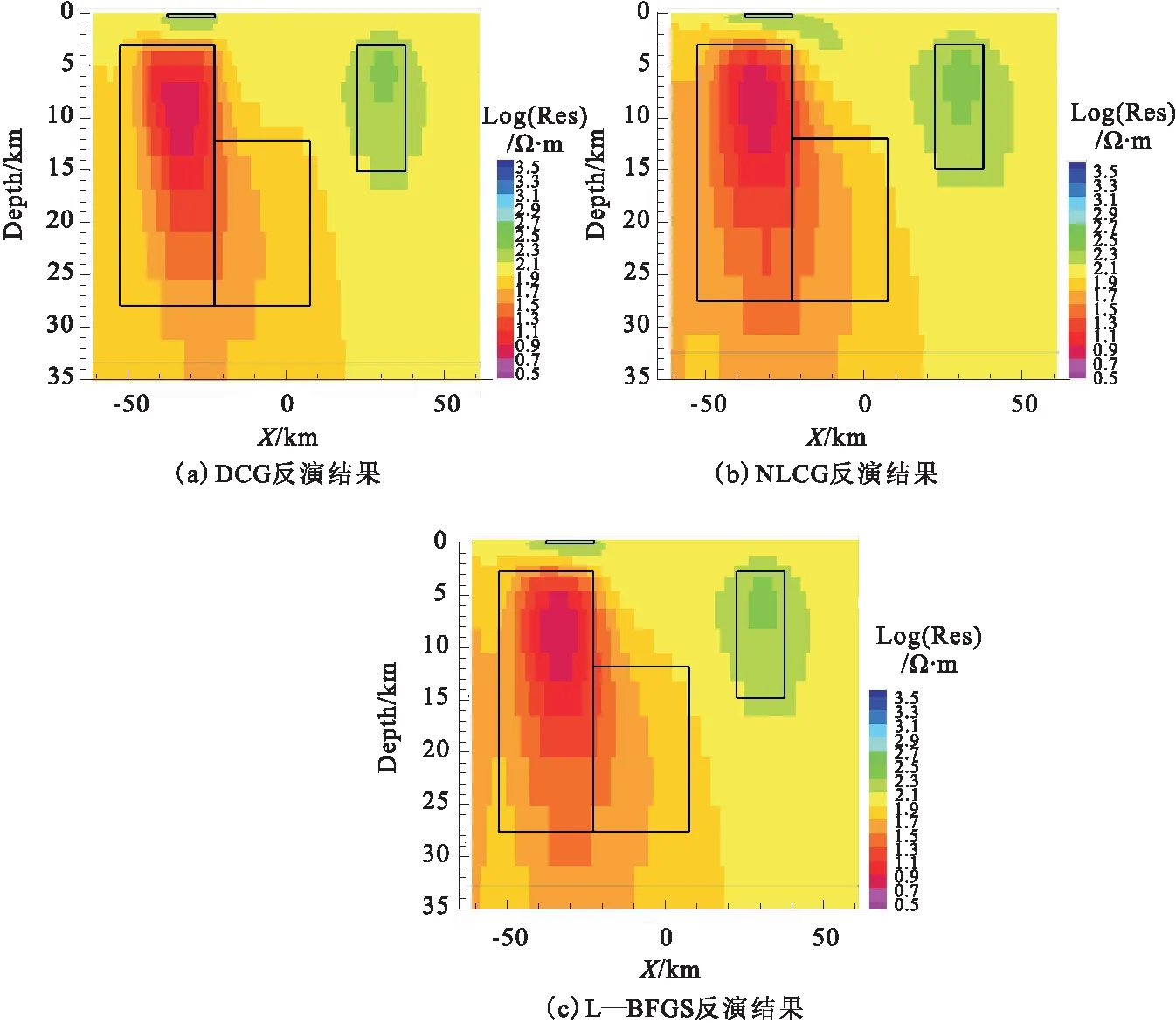
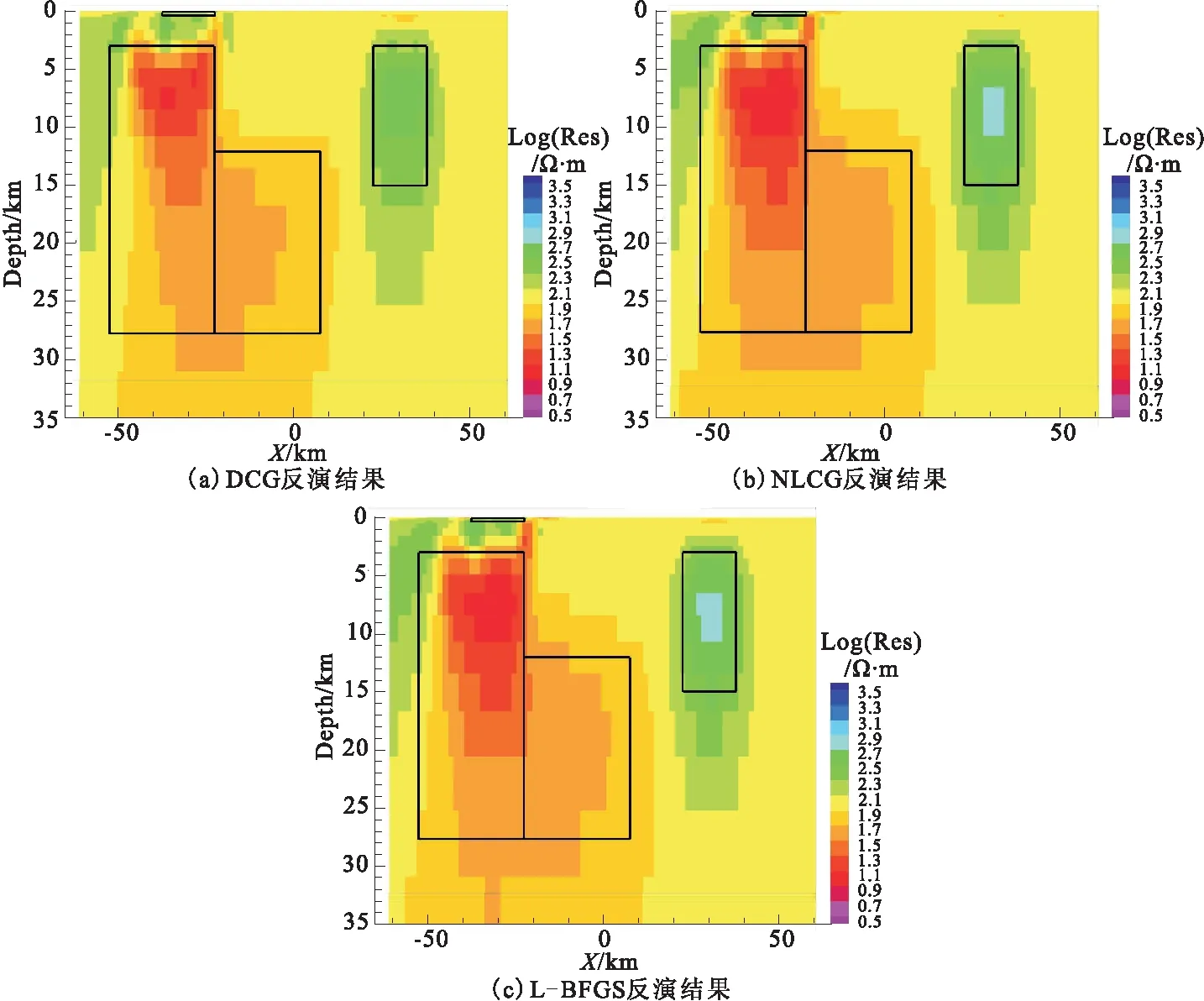
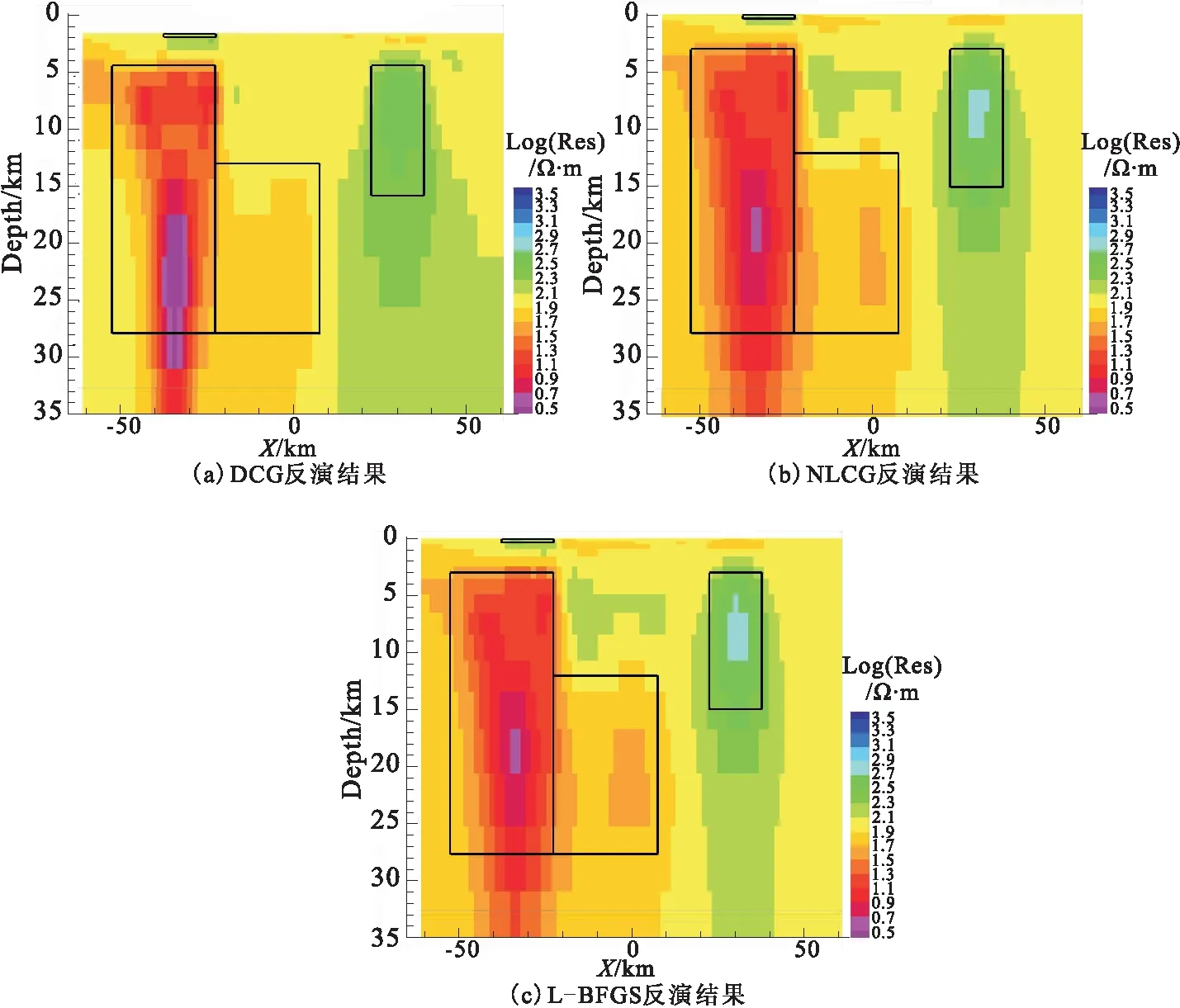
10)若|(rk+1)| 13)dn、bn、xk、yk、pk、rk等是数据空间共轭梯度反演中的向量,αk和βk是标量步长。在进行DCG反演的时候,对于Ck的选取非常重要[2]。其中γk是一个特定的标量。选择合适的Ck,可使共轭梯度算法的迭代次数大大减少,从而降低反演时间、提高效率。 随着大地电磁反演方法的不断发展,相关学者提出利用CG求解线性方程组,并将该方法用于求解无约束最优化问题。非线性共轭梯度法(NonlinearConjugateGradient,NLCG)与CG算法相比,它们的基本理论大体一致。NLCG广泛应用于大地电磁反演中,是解决非线性最优化问题的一种方法,并已在实际大地电磁资料解释中取得了较好的应用效果。 NLCG目标函数为 φ(m)=(d-F[m])TV-1(d-F[m])+λmTLTLm (13) 其中,F为正演函数;V为误差向量方差的正定矩阵;L是二阶差分拉普拉斯算子。 迭代过程为 (14) 式中,步长αk利用一维搜索确定,搜索方向经过迭代产生,表达式为 (15) (16) 由此可知,NLCG的主要计算量在于计算梯度和步长,步长的选取标准是使得目标函数满足一定条件时就搜索[5]。当没有先验条件时, 令Ck=I。 在NLCG算法中,在进行每一次迭代时有下式 (17) (18) 本文采用另外一种非标准的计算策略,具体表达式为: (19) 该表达式满足Wolfe条件,也能够快速找到局部最小值点,这是它最大的好处。不难得出,在每次迭代中需要计算梯度一次以及目标函数若干次,这与最速下降法是非常相似的。 表1 NLCG算法Table 1 The flow of NLCG algorithm 随着大地电磁反演的发展,相关学者用DFP 算法来构建该近似矩阵,提出一种新型的拟牛顿算法,简称BFGS法,但该方法仍然需存储矩阵,使得反演时间增加,效率降低。针对这一问题,相关学者在此基础上,提出L-BFGS法,该算法的优点是:构建近似的Hessian矩阵,只利用最近一次迭代的曲率信息。 (20) (21) 通过重复计算式(2)~式(20)式,L-BFGS 近似 Hessian 矩阵的表达式可表示为[5]: (26) (27) 表2 L-BFGS双递归算法流程Table 2 The flow of L-BFGS double recursive algorithm 表3 L-BFGS算法流程Table 3 The flow of L-BFGS algorithm 为了验证DCG、NLCG、L-BFGS这三种不同大地电磁二维反演方法各自的优缺点,本节以理论模型试验为例进行分析。通过设计两个理论地电模型——高、低阻体组合模型和复杂组合模型,用上述三种方法分别进行反演,最后对比分析反演效果。 设计了一个含有高阻异常体和低阻异常体的组合模型,在模型中围岩电阻率为100 Ω·m,范围是均匀半空间。包含两个异常体(图1),分别是:电阻率为10 Ω·m的低阻异常体,宽度为30 000 m,厚度为15 000 m,水平方向上的位置为-30 000~0 m,深度方向上的位置为0~15 000 m;电阻率为1 000 Ω·m的高阻异常体,宽度为30 000 m,厚度为15 000 m,水平方向上的位置为0~30 000 m,深度方向上的位置为0~15 000 m,如图1所示。此模型反演所用的数据是TE、TM、Tzy三种不同模式下的响应数据,并且对电阻率加入了5%的噪音,在相位上加入了1.45度的噪音。其中测点总共40个,点距是2 500 m,每个测点上的频点数为12,频率范围为0.001~3.333 Hz。 3.1.1 反演模型结果对比分析 反演所用数据是,TE、TM、Tzy三种不同模式下的响应数据,下面一一列举,见图2~图4。 图2 TE模式下不同方法反演的电阻率断面Fig.2 Resistivity profile of different inversion methods in TE mode 图3 TM模式下不同方法反演的电阻率断面Fig.3 Resistivity profiles retrieved by different methods in TM mode 图4 Tzy模式下不同方法反演的电阻率断面Fig.4 Resistivity profiles retrieved by different methods in Tzy mode 对不同极化模式下的响应数据采取三种不同方法进行反演,得到以上结果。与真实模型相比,TM模式的三种反演方法的反演结果基本上恢复了异常体的位置、尺寸,低阻异常体的反演电阻率与真实的非常相近,三种方法反映高、低阻异常体的电阻率值都会有一定的偏差,异常都会向四周发散,不同反演方法都能较好的恢复地电模型。NLCG和L—BFGS对高阻异常体的反演较好,反演效果差不多,能大致恢复高阻异常体的尺寸与电阻率值,但三种方法对高阻异常体的反演电阻率都偏小。 3.1.2 不同反演算法迭代情况 由表4可知,迭代过程中,随着迭代次数的增加,RMS值都呈下降状态,RMS的不断减小,进一步说明三种方法收敛性都很好。NLCG比DCG、L-BFGS的RMS值减小更快、收敛速度更快。但是随着迭代次数增加,三种反演方法不断收敛的过程中,它们的RMS值都趋于1,表示三种反演方法都有较好的收敛性。 表4 高、低阻模型模式反演算法迭代情况 设计了一个复杂模型(图5),在模型中研究区域为100 Ω·m的均匀半空间,包含四个异常体,分别是: 1)电阻率为10 Ω·m的低阻异常体,宽度为30 000 m,厚度为25 000 m,水平方向上的位置为-50 000~-20 000 m,深度方向上的位置为3 000~28 000 m; 2)电阻率为10 Ω·m的低阻异常体,宽度为25 000 m,厚度为15 000 m,水平方向上的位置为-20 000~5 000 m,深度方向上的位置为13 000 m~28 000 m; 3)电阻率为1 000 Ω·m的高阻异常体,宽度为10 000 m,厚度为10 000 m,水平方向上的位置为25 000~35 000 m,深度方向上的位置为4 000~14 000 m; 4)电阻率为1 000 Ω·m的高阻异常体,宽度为10 000 m,厚度为1 000 m,水平方向上的位置为-30 000~-20 000 m,深度方向上的位置为0~1 000 m。 此模型反演所用的数据是TE、TM、Tzy三种不同模式下的响应数据,并且对电阻率加入了5 %的噪音,在相位上加入了1.45度的噪音。其中测点总共40个,点距是2 500 m,每个测点上的频点数为12,频率范围为0.001~3.333 Hz。 3.2.1 反演模型结果对比分析 反演所用数据为TE、TM、Tzy三种不同模式下的响应数据,下面一一列举,见图6~图8。 图6 TE模式下不同方法反演的电阻率断面Fig.6 Resistivity profile of different inversion methods in TE mode 图7 TM模式下不同方法反演的电阻率断面Fig.7 Resistivity profile of different inversion methods in TM mode 图8 Tzy模式下不同方法反演的电阻率断面Fig.8 Resistivity profile of different inversion methods in Tzy mode 对不同极化模式下的响应数据采取三种不同方法进行反演,得到以上结果。与真实模型相比,三种反演方法的反演结果对异常体的位置、尺寸都可以大致地恢复出来,不同反演方法都能较好地恢复地电模型。Tzy模式时,相对于DCG的反演结果,NLCG和L-BFGS反演结果更能反映出异常体的尺寸与电阻率的真实值。在反演的电阻率数值上,三种方法反映高、低阻异常体的电阻率值都会有一定的偏差,异常都会向四周发散。NLCG和L-BFGS对高阻异常体的反映较好,能大致确定高阻异常体的尺寸与电阻率值,但三种方法对高阻异常体的反演电阻率都偏小。L-BFGS和NLCG总体反演效果相当,L-BFGS更适合复杂介质模型。 3.2.2 不同反演算法迭代情况 由表5可知,迭代过程中,随着迭代次数的增加,RMS拟合差值都呈下降状态,RMS不断减小,进一步说明三种方法收敛性都很好。NLCG比DCG、L-BFGS的RMS拟合差值减小更快、收敛速度更快。而随着迭代次数增加,三种反演方法不断收敛的过程中,它们的RMS值都趋于1,表示三种反演方法都有较好的收敛性。但对于复杂地电模型,L-BFGS能获得更小的RMS拟合差。 表5 复杂模型反演算法迭代情况 本文通过对大地电磁不同二维反演算法的研究,从麦克斯韦方程组出发,利用理论模型正演响应的数据进行反演,对DCG、NLCG、L-BFGS三种反演算法的反演效果进行了比较,得到了以下结论: 1)通过对高、低阻模型和复杂模型的反演对比可以看出,三种方法均能较好地反演出异常体的位置以及大小,但是对异常体电阻率的反演值与理论真实值之间总存在一定偏差,这是不可避免的;同时,三种方法反演效果大体相当,无论是低阻异常体还是高阻异常体都会向四周发散,L-BFGS和NLCG总体反演效果相当。 2)通过对高、低阻模型和复杂模型的反演,三种方法在迭代过程中,数据拟合差RMS值都呈不断下降状态。NLCG比DCG、L-BFGS的RMS值减小更快、收敛速度更快。随着迭代次数增加,它们的RMS值最后都趋于1,表示三种反演方法都有较好地收敛性,但是对于复杂地电模型,L-BFGS的反演效果更好。 3)由于不同反演方法各有自己的特点,所以在实际选择方法时要考虑其优缺点,从而更好的发挥不同反演方法的优点;同时,反演算法的运行速度和所需内存不一样,进行算法设计时候,应该充分考虑到这一点,从而让大地电磁反演工作效率更高。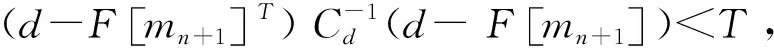
2.3 非线性共轭梯度法 (NLCG)反演
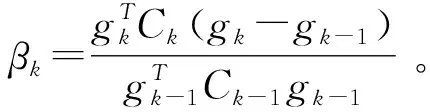
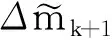

2.3 有限内存拟牛顿法 (LBFGS)反演
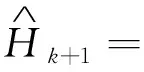
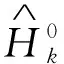
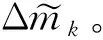


3 理论模型反演对比分析
3.1 高、低阻体组合模型

3.2 复杂模型

4 结 论
