基于节段预制拼装施工阶段的PK箱梁剪力滞效应研究
2022-02-21赵健
赵 健
(中国铁建大桥工程局集团有限公司 天津 300300)
1 引言
PK箱梁由于具有造型美观、抗风性能好的特点,在大跨度桥梁中得到了广泛应用[1-2]。该梁型的设计理念在美国被提出后,逐渐在斜拉桥结构中推广使用。统计资料显示,在跨径达到800 m以上的斜拉桥,混合梁斜拉桥数量占比80%以上,而采用PK箱梁作为主梁结构的斜拉桥在大跨度混合梁斜拉桥数量中占比约37.5%,该数据充分体现了PK箱梁在大跨度斜拉桥中具有较高的使用率和较好的适用性。近年来,采用PK箱梁的斜拉桥数量日益增多,但由于结构宽度大,荷载作用时常引起较大的剪力滞效应,对结构安全性造成一定的影响,严重时可能发生局部破坏,该问题倍受工程师和学者们关注。徐华等[3]对斜拉桥成桥状态下PK箱梁剪力滞效应进行了分析,结果表明在恒载和活载作用下位于索塔的箱梁顺桥向剪力滞效应较大。徐重财等[4]分析了斜拉桥PK箱梁结合段的剪力滞效应,论述了钢混结合段剪力滞效应的分布规律。谢芬等[5]采用数值模拟方法研究了斜拉桥悬臂施工阶段PK箱梁的剪力滞效应,计算结果显示在斜拉索挂设时腹板剪力滞效应最为明显。乔朋等[6]对PK箱梁结构设计参数的取值范围进行了研究,应用回归分析法提出了PK钢箱梁剪力滞的实用计算公式。李飞等[7]对服役中的斜拉桥PK箱梁剪力滞效应进行了研究,阐述了该梁型的病害很可能是由设计与施工工艺存在缺陷而引起的,并提出了加固、改造的思想。
综上所述,PK箱梁的剪力滞效应问题仍值得探索,尤其是施工阶段对结构剪力滞效应的影响相关研究内容较少。本文以石首长江公路大桥边跨主梁施工为背景,对PK混凝土箱梁在节段预制拼装施工阶段受力体系转换进行分析,集中对剪力滞效应展开研究,采用空间计算理论和现场实测的方法对研究结果进行验证,为同类桥梁施工控制提供理论支撑。
2 结构概况
石首长江公路大桥为主跨820 m的双塔非对称混合梁斜拉桥,主桥桥跨布置为(75+75+75)m+820 m+(300+100)m(见图1)。北边跨主梁截面形式为PK断面箱梁,长251.5 m[8-11],PK箱梁顶板、底板和隔板内设有横向预应力,均采用高强度低松弛钢绞线,公称直径为φ15.2 mm,标准抗拉强度fpk=1 860 MPa,腹板设有竖向预应力,采用直径φ50 mm,标准强度为fpk=830 MPa,截面参数与预应力钢束布置见图2。北边跨主梁采用节段预制拼装施工工艺,首先在边跨97~100号墩之间设置预制场,预制台座采用组合式移动模板进行PK箱梁节段预制,然后利用特种龙门吊机将箱梁节段提升至墩顶滑移支架,滑移至指定位置,最后进行节段拼装施工。
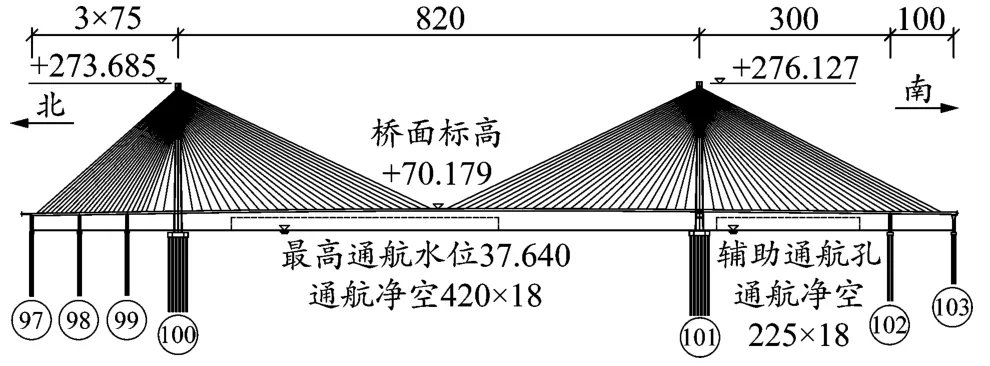
图1 石首长江公路大桥主桥布置(单位:m)

图2 截面参数与预应力布置(单位:m)
3 剪力滞效应产生机理
剪力滞效应与PK箱梁结构几何特性、边界条件及外界荷载作用存在密切关系,在施工过程中箱梁由结构受力体系改变引起内力重分布,导致出现剪力滞效应,影响结构的安全性,存在局部破坏的可能性。在节段预制拼装施工阶段PK箱梁不受外部荷载影响,但受自重及预应力钢束作用影响。对于PK混凝土箱梁而言在保证边界条件对称的前提下,左右幅箱梁顶、底板及腹板受力成对称状态,弯曲与剪切变形规律近似相同,因此截面正应力流传递相等。但是,由于PK混凝土箱梁结构中设有“空间预应力”,剪力滞效应的复杂化难以确定,想要准确得到计算结果需要重点考虑预应力与边界条件变化耦合作用。根据节段预制拼装施工阶段划分,PK箱梁主要分为“自重作用”、“箱梁提升”与“支架上滑移”三种受力模式,施工阶段划分与边界条件见表1。
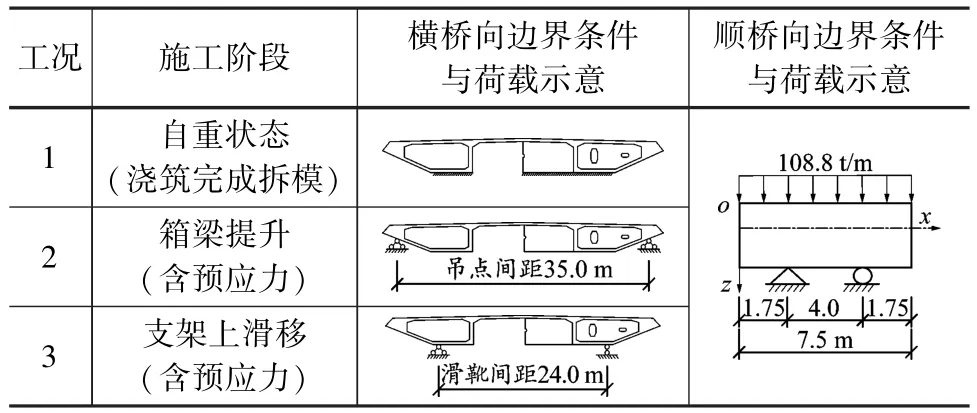
表1 施工阶段划分与边界条件
4 空间有限元模型
PK混凝土箱梁节段空间有限元模型采用精细化有限元软件进行模拟,模型划分采用四边形网格,由10 113个节点,31 875个实体单元以及200个杆单元建立而成(见图3a)。预应力钢束采用3DB样线条进行模拟,钢束与混凝土结构单元通过程序进行自动耦合(见图3b)。每个预应力钢束划分为20个节段,节点用于形成虚拟孔道,为预应力钢束受力方向提供引导作用,其中混凝土材料按C55选取弹性模量E=3.4 ×106t·m,泊松比选取0.2[12],箱梁顶板、底板与横隔板预应力钢束弹性模量选取195 GPa,腹板预应力钢束选取200 GPa,泊松比为0.3。计算考虑理想状态下同步、对称张拉预应力,未考虑普通钢筋对结构刚度的变化影响。模型假设梁体混凝土材料各向均质同性、密实,箱梁结构模型见图3,设计预应力张拉量见表2。

图3 混凝土PK箱梁结构模型

表2 预应力设计张拉量
5 现场实测与模型精度验证
为验证PK混凝土箱梁有限元模型计算精度,分析箱梁在施工阶段应力状态的变化趋势,采用在箱梁布置应变传感器的方法进行应力监测。根据PK箱梁结构受力特征,选取结构应力变化敏感性较强的顶板位置监测,在顶板横桥向布置6个传感器(M1~M6),顺桥向布置6个传感器(Z1~Z6),共计12个传感器,测点布局见图4,箱梁应力状态监测与模拟结果对比曲线见图5、图6。

图4 PK箱梁测点布局(单位:m)
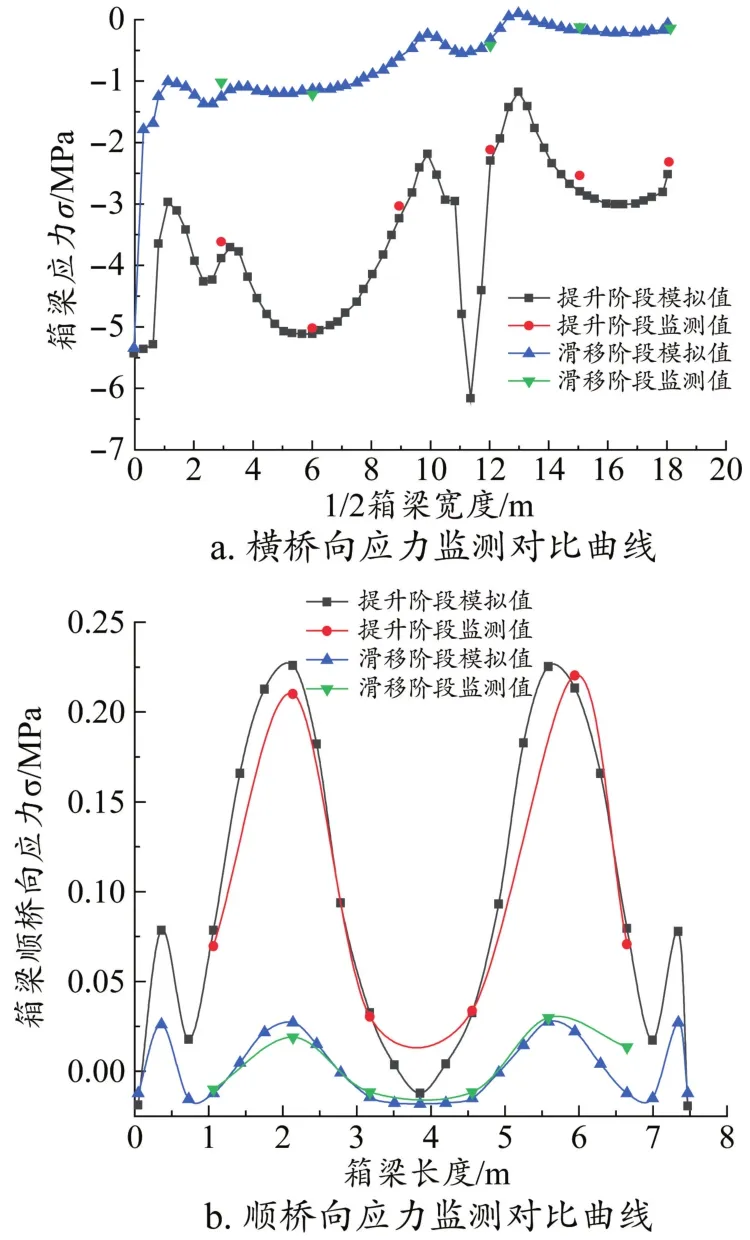
图5 PK箱梁应力监测与数值模拟对比结果

图6 横向预应力对PK箱梁剪力滞系数影响曲线
通过对PK箱梁在提升与滑移阶段实测值与模拟值对比曲线可见,实际监测纵向弯曲应力沿横、纵桥向的分布规律与有限元模拟结果吻合良好,误差范围在6%~7%之间,该误差可能是由于测量仪器的精度、空气温度、太阳辐射以及结构特性与模型选取的材料、几何参数不一致等综合因素所致。鉴于模型参数选取符合规范标准,且具有明确的物理意义,已经可以满足实际工程结构计算分析的需要,所以在此不对模型进行修正处理。
6 剪力滞计算结果分析
选取结构顶板为例进行分析,根据材料力学初等理论与考虑结构实际受力状态的空间有限元计算理论,得到截面局部应力的比值λ作为评定PK箱梁结构剪力滞效应的主要指标。剪力滞系数λ的计算公式表示为:
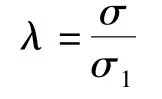
式中,σ1为初等理论计算的截面平均应力;σ为空间计算理论得到的截面应力(本文采用实体模型中的节点应力)。
计算结果图6显示,无预应力状态下PK箱梁顶板剪力滞效应较大,靠近风嘴和腹板两侧位置各出现了峰值,最大剪力滞系数达到3.2,结构空腔位置4~9 m与15~19.25 m范围内出现负剪力滞效应,最小剪力滞系数为0.1;在设计张拉力50%作用下,箱梁锚固区位置剪力滞系数达到4.0,腹板剪力滞系数为3.25,这是由于横向预应力和腹板竖向预应力集中作用在锚点引起的应力突变,导致剪力滞效应增大;结构位置0.5~6.5 m范围内出现负剪力滞效应,最小剪力滞系数为0.02,其余部位剪力滞效应均小于无预应力状态;当预应力达到设计张拉力100%时,0~9 m区域呈正剪力滞效应,9~19.25 m范围呈负剪力滞效应;各部位剪力滞系数曲线变化趋于平缓,整体表现小于前两种状态,说明顶板与横隔板预应力钢束对降低结构剪力滞效应作用明显。
通过对比横桥向三个施工阶段的剪力滞系数变化曲线(见图7a),发现自重作用下剪力滞效应最大,提升与滑移阶段剪力滞效应相对较小。其中,提升阶段剪力滞效应最大为1.75,位于腹板处;滑移阶段最大剪力滞系数为1.7,出现在靠近风嘴位置。对比箱梁提升与滑移阶段剪力滞系数曲线,发现PK箱梁横桥向0~6 m范围内,在提升状态转为滑移状态时剪力滞系数最多增大约32%,6~18 m范围内剪力滞系数最多减小75%,其主要原因是PK箱梁吊点与滑靴位置转换引起剪力滞沿横向分布变化。
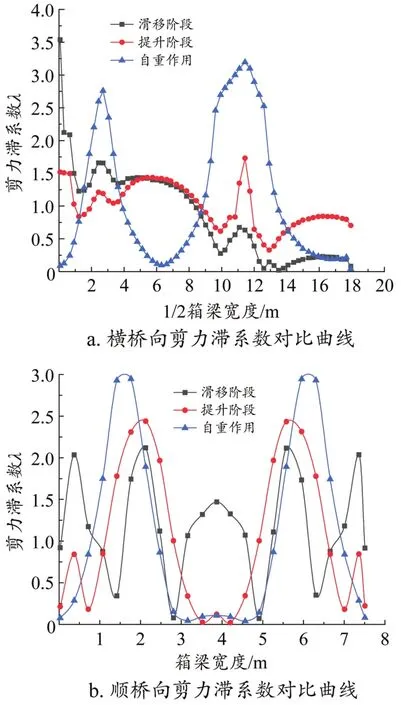
图7 施工阶段PK箱梁剪力滞系数对比曲线
自重作用时PK箱梁剪力滞系数峰值位于两侧横隔板(见图7b),最大为3.15,中间截面呈负剪力滞效应,最小系数为0.1;箱梁在提升时剪力滞系数峰值最大为2.5,中间截面呈负剪力滞效应,最小系数为0.05;滑移阶段横隔板位置剪力滞系数减小到2.2,剪力滞峰值向箱梁中部略微移动,中间截面剪力滞系数最大为1.5,其原因是受顶板与横隔板预应力影响产生上拱,边界条件发生改变共同作用所致。
7 结论
(1)通过PK箱梁现场实测与有限元模拟结果进行对比,发现采用考虑空间预应力的结构模型计算结果与实测结果吻合较好,误差在6%~7%之间,同时证明了剪力滞系数的计算结果基本符合工程实际情况。
(2)PK箱梁在自重状态下结构应力较小,但剪力滞效应最大,在提升与滑移阶段的剪力滞效应相对较小,且沿箱梁截面呈非线性走势;在预应力作用相同的情况下,吊点与滑靴位置的改变是影响剪力滞效应的主要因素。
(3)横向预应力越大,剪力滞系数曲线沿横桥向越趋于平缓,当预应力达到一定张拉量时,可以改变结构的正、负剪力滞效应区范围,说明顶板与横隔板预应力钢束提供的压应力对剪力滞效应的影响效果明显。
(4)建议在设计节段预制拼装施工方案时,对预应力张拉方法以及吊点与滑靴位置的设置予以充分考虑,控制箱梁剪力滞效应,保障施工阶段结构的安全性。
