高阶对流Cahn-Hilliard型方程的二阶线性化差分方法

李娟

（南京审计大学金审学院基础部，江苏 南京 210023）

0 引言

SEVINA等［1］在描述具有小斜面生长中的晶体表面时提出了一类高阶对流Cahn-Hilliad型方程。考虑高阶对流Cahn-Hilliard型方程的周期初边值问题：

其中，x、t分别为空间和时间，u为界面斜率，ε与原子通量的沉积强度成正比，整体对流项εuux来自于堆积原子的法向冲击，uxxxxxx来自于曲率微分正则化，其他项表示表面扩散作用下表面能的各向异性。

高阶对流Cahn-Hilliard型方程在材料模拟中具有重要作用。KORZEC等［2］研究了该方程的稳态解；KORZEC等［3］利用Galerkin方法研究了方程弱解的存在性。由于高阶非线性发展方程较难求解析解，故研究数值算法具有一定意义。

因对高阶对流Cahn-Hilliard方程的相关数值研究较少，故本文先探究六阶非线性发展方程相场模型的数值方法。WISE等［4］和HU等［5］分别基于凸分解方法讨论了晶体相场模型的时间方向一阶、空间方向二阶的稳定数值格式和二阶非线性三层差分格式；GOMEZ等［6］和ZHANG等［7］分别讨论了能量稳定的数值格式和二阶差分格式；由于非线性格式迭代运算耗费时间较多，YANG等［8］、CAO等［9］和李娟［10］分别讨论了晶体相场模型的线性化数值算法。高阶对流Cahn-Hilliard型方程较之于晶体相场模型，前者具有非线性对流项和扩散项，且导数达到四阶，这对模型数值算法的建立及理论分析均带来了实际困难。为解决这些问题，需改写方程中的非线性项。本文利用中心差商对其进行离散，一方面方便差分格式线性化，另一方面，在差分格式的理论分析中避免对非线性项差商的估计，这在一定程度上降低了分析难度。

为丰富高阶非线性发展方程的数值算法，研究了高阶对流Cahn-Hilliard型方程的线性化差分方法。首先，建立二阶收敛的线性化差分格式；其次，利用能量分析方法和数学归纳法对差分格式进行理论分析，证明差分格式解的唯一性和L2范数下的收敛性。再次，利用数值算例验证差分格式的有效性。最后，给出了小结和展望。

1 差分格式的建立

为建立二阶线性化差分格式，引入以下记号：正整数M，N，时间区间[0，T]。记xi=ih，tk=kτ，Ωh={xi|0≤i≤M}，Ωτ={tk|0≤k≤N}，Uh={v|v={vi}，vi=vi+M}。对任意网格函数v∈Uh，记

对定义在Ωτ上的网格函数w=(w0，w1，w2，…，wN)，记

对式（1）和式（2）在周期[0，L]上建立差分格式。用网格函数Uki表示问题的精确解在点(xi，tk)处的值。由泰勒公式，有

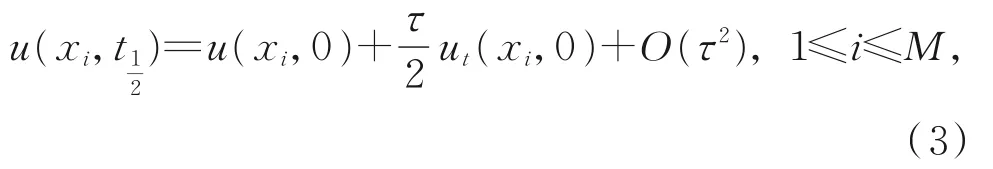
其中，ut(xi，0)由式（1）和式（2）确定，并记

因uux=3u2)ux]xxx，故式（1）等价于

其中，f(u)=1-3u2。分别在点和(xi，tk)处对式（5）应用带积分型余项的泰勒公式，可得

假设式（1）和式（2）的精确解适当光滑，则存在正常数c0，使得

在式（6）～式（8）中，用数值解代替精确解，并略去小量项，可得以下线性化隐式差分格式：

综上，对式（1）和式（2）建立了线性化隐式差分格式，即式（10）～式（12）。第0层的数值解由初值条件式（12）给出；式（10）为关于第1层数值解u1的变 系 数 线 性 方 程 组；当uk-1，uk（k≥1）已 知 时，式（11）为关于第k+1层数值解uk+1的变系数非齐次线性方程组，利用线性方程组理论可求得该时间层的数值解。

2 差分格式的理论分析

利用能量分析法讨论差分格式的唯一可解性和收敛性。为便于分析，定义内积和范数，并给出一些引理。

对任意的u，v∈Uh，定义

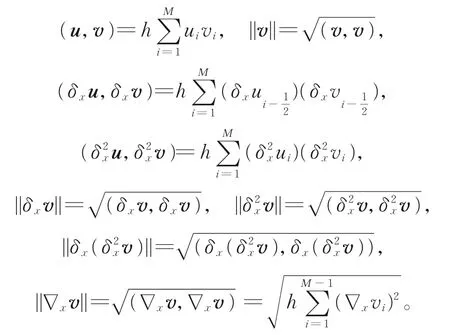
引理1［11］对任意的u，v∈Uh，存在

由引理1和内积定义，可知

从而有

引理2对任意的u，v∈Uh，有

引理3［4］设v，∈Uh，对任意的正数α＞0，有

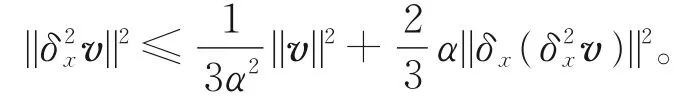
记

定理1假设式（1）和式（2）的解适当光滑，则式（10）～式（12）是唯一可解的，且按L2-范数收敛于问题的精确解，收敛阶为O(τ2+h2)。即存在正常数c，当时，有

证明数学归纳法。

第1步u1的唯一性。

由式（12）知，第0层的数值解u0已唯一确定，此时，式（10）为关于u1的线性方程组，欲证其唯一可解性，仅需证其对应的齐次线性方程组

仅有零解。

用u1与式（18）作内积，可得

由柯西不等式、引理1、引理2及式（19），知

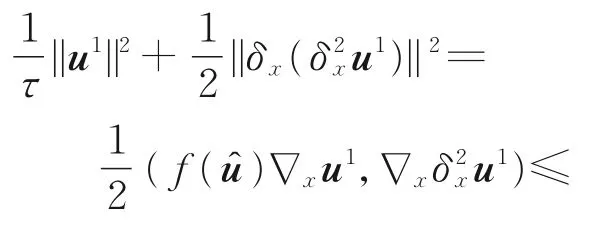
在引理3中，取α=3，可得

从而有

将式（22）代入式（20），可得

第2步u1的收敛性。

由引理1、引理2及当α=3时的引理3，并将式（17）代入式（24），可得

从而有

当τ≤时，由 式（26）可得

假设对第0，1，2，…，l层数值解，定理结论均成立，则当时，有

从而有

第3步ul+1的唯一性。

当uk、uk-1已知时，式（11）为关于uk+1的线性方程组。欲证其唯一可解性，仅需证其对应的齐次线性方程组

仅有零解。

用uk+1与式（29）作内积，可得

由引理1、引理2及式（30），可得

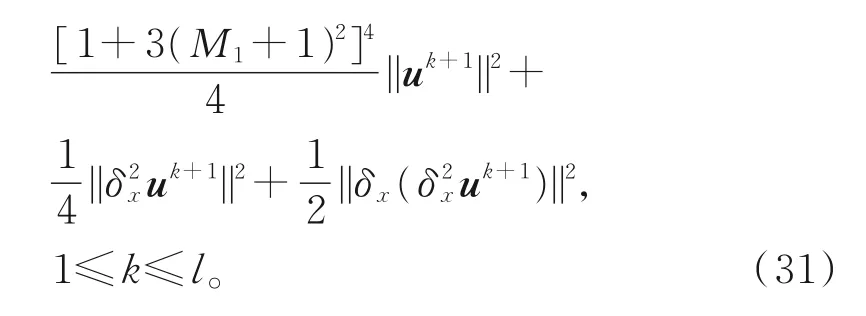
由当α=3时的引理3及式（31），可得

从 而，当τ时，有||ul+1||2=0，即第l+1层数值解是唯一的。

第4步ul+1的收敛性。

用e-k与式（14）作内积，可得

由引理1和式（33），可得

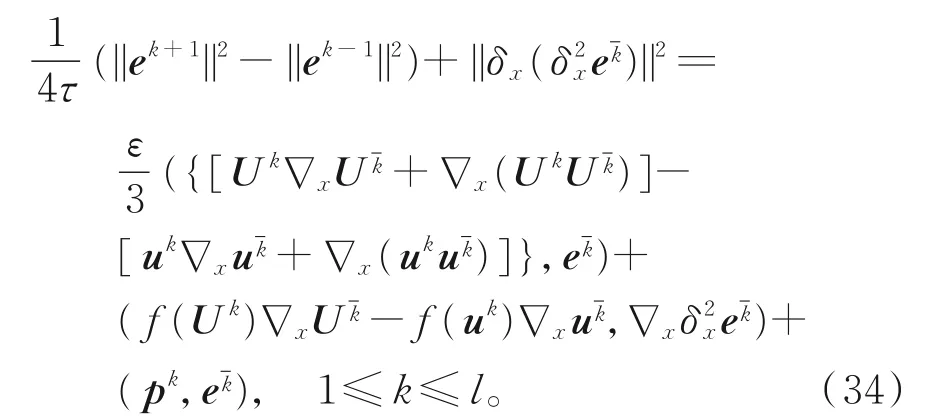
先估计非线性项：

由引理2和柯西不等式，可得

由

及引理1和柯西不等式，可知

将式（36）、式（38）代入式（34），可得

在引理3中，取α=，有

将其代入式（39），整理后可得

记Ek=||ek||2+||ek+1||2，由式（40），有

由Gronwall不等式、式（9）、式（27）及式（42），可得

即

从而有

即对第l+1层数值解，定理成立。

证毕。

3 数值算例

式（10）～式（12）在时间和空间上均为二阶收敛。每个时间层仅需解一个线性方程组。设{uki(h，τ)|1≤i≤M，0≤k≤N}为式（10）～式（12）的数值解，为验证数值误差和收敛精度，分别定义L2-范数和L∞-范数下的误差：

对于充分小的空间步长h，定义时间收敛阶：

对于充分小的时间步长τ，定义空间收敛阶：

KORZEC等［3］分 别 研 究 了 参 数ε=0.01，0.5，0.7，1，2，3，5时式（1）和式（2）解的演化情况。对参数ε=0.5，初 值u0(x)=sin(2πx/64)，在 周 期 区 间［0，64］，时间区间［0，T］内，利用Matlab编程验证数值解的收敛性。

首先，固定空间步长h，验证时间收敛阶。取空间网格点数M=2 000，时间网格点数N=20，40，80，160，分别计算时刻T=5的误差H2（h，τ），H∞（h，τ）和时间收敛阶order1，order2，数值结果见表1。其次，固定时间步长τ，验证空间收敛阶。取时间网格点数N=2 000，空间网格点数M=10，20，40，80，分别计算时刻T=5时的误差H2（h，τ），H∞（h，τ）和空间收敛阶order3，order4，数值结果见表2。由表1和表2可知，差分格式是二阶收敛的，验证了差分格式的有效性。

表1 当T=5，M=2 000，ε=0.5时，差分格式在L2-范数和L∞-范数下的误差和时间收敛阶Table 1 The errors and temporal convergence orders of the difference scheme in L2-norm and L∞-norm when T=5，M=2 000，ε=0.5

表2 当T=5，N=2 000，ε=0.5时，差分格式在L2-范数和L∞-范数下的误差和空间收敛阶Table 2 The errors and spatial convergence orders of the difference scheme in L2-norm and L∞-norm when T=5，N=2 000，ε=0.5

4 结论

研究了高阶对流Cahn-Hilliard型方程的数值方法。建立了二阶收敛的线性化差分格式，利用能量分析方法证明了差分格式的唯一可解性和L2范数下的收敛性，由数值算例可知，数值解在最大模意义下亦是二阶收敛的。差分格式的研究方法可推广至二维情形。对于高阶对流Cahn-Hilliard型方程的差分格式算法仅研究至二阶，为提高计算精度，后续将研究该问题的高阶线性化数值格式。