基于融合分布图网络的触觉压力足迹分类方法

张艳 高梓健 许昌康 王年† 鲁玺龙

(1.安徽大学 电子信息工程学院，安徽 合肥 230601；2.公安部物证鉴定中心，北京 100038)

生物特征识别技术用于身份识别、门禁系统以及重点防控对象[1]。生物特征识别技术应用的基本前提为对象是唯一的，通过其独特的生理特征和行为特征来识别每个对象[2]。随着生物特征识别技术的广泛应用，人们需要更独特、更方便和用户友好性的识别技术。人体足迹压力因其稳定性和独特性使其成为一种较新的生物特征，并且已经验证了其唯一性[3]。触觉压力足迹是指对象在站立或行走时，脚掌面通过力的传递作用在压力采集器上反馈的压力值分布[4]。触觉压力足迹可以反映对象的身高、体重、年龄等生理特征和行为习惯，因此研究者可以在一定程度上根据触觉压力足迹图像分析对象形态特征和分类，也能为刑侦、医疗、安保等领域带来便捷，这就要求研究者具有大量的足迹专业知识和大量训练，因此若想进行大范围推广具有较大的难度。

近几年，卷积神经网络因其强大的建模能力得到快速发展。相比传统方法，卷积神经网络的引入给图像处理和自然语言处理等领域带来了很大的提升，如图像分类、目标识别、语音识别等[5- 8]。Wang等[9]针对人体触觉压力足迹分布面，提出了一种基于高斯曲率和平均曲率的触觉压力足迹曲面提取方法，并以此为基础，提出了能够反映人体生理特征的一种基于足迹图像整体特征和局部特征的表达方法。梁栋等[10]借助足底不同区域的压力点最大值、压力中心点的坐标和压力值来提取拉普拉斯谱特征，同时结合足底轮廓及压力比值特征，提出一种静态触觉步态识别方法，该方法可以用于门禁和考勤系统。Kulkarni等[11]采用贝叶斯正则化反向传播训练的多层感知机，对人体触觉压力足迹图像依据像素值进行分类，该方法用于区分平足、普通足和高弓足，有助于研究步态分析和运动生物力学。Keatsamarn等[12]应用深度学习中的几个卷积层提取触觉压力足迹图像的特征图，达到分类的目的，在一定程度上缓解了触觉压力足迹图像分类需要专业人士才能实现的问题。

图神经网络可用来处理数据类型关系图。Garcia等[13]针对小样本学习设计出图卷积网络，其中支持集中所有样本都和查询集建立一定的关系，每个输入节点都由嵌入网络提取后的卷积特征和给定的标签信息表示，通过图网络的聚合功能更新节点特征来传播标签信息。Kim等[14]针对图网络中边的特殊性，基于样本类内相似性和类间相异性提出了边缘标签图神经网络(EGNN)，通过节点和边的交替更新得到边的预测结果。Yang等[15]通过建立样本的分布级表示，构成分布传播图网络(DPGN)，同时建立图上的样本级关系和分布级关系，在双图循环更新中将带标签信息的样本传播到不带标签的样本，得到边的预测结果。

单样本学习和多样本学习是通用的两种学习范式，都可以对哪个标签可以描述实例做出回答，但是都不能对每个标签的实例描述程度有多大做出回答[16]。标签分布学习最早由Geng[17]提出，目的是找到一种可以表示每个标签描述实例相对重要性的算法。深度标签分布学习将每幅图像标签转换为离散标签分布，并利用深度卷积将预测的标签分布和基准真值标签分布之间散度最小化，以进行学习标签分布[18]。基于面部的情绪分布学习利用了可以在一定程度上解决‘如何描述情感’糊性的标签分布学习法，并且提出了局部利用标签相关性的分布学习法[19]。条件概率神经网络框架输入是样本和标签，输出是一个隐层的标签分布[20]。文献[15]根据标签分布学习规则[17]，首次在图神经网络中提出分布级表示，以样本在每类占据的重要程度，将一个样本的分布级关系建模到其他样本，通过设计的双图网络交替更新来建立样本相似度和样本分布的关联，实现了样本卷积特征向量和分布关系的混合。

本研究根据标签分布和标签one-hot向量权值和为1的特殊性，提出了一种融合分布图结构。采用小样本训练策略在一定程度上克服了触觉压力足迹中样本数量的问题。首先利用嵌入网络提取样本的卷积特征，通过范数化和正则化得到样本相关性矩阵。其次利用标签one-hot向量来构建类间相关性矩阵。最后利用卷积核将样本相关性矩阵和类间相关性矩阵进行融合，并且用标签分布的准则生成分布图的节点特征。样本相关性矩阵和标签相关性矩阵分别包含了样本间和类别间的相关性信息，依据标签分布准则在分布模块中将样本相关性矩阵和标签相关性矩阵进行融合重分配，提升了样本在网络中的初始表达能力，同时提升了样本分布关系的区分度，从而更好地在标记样本和未标记样本之间建立关联。本研究提出的方法，在触觉压力足迹数据集上5-way1-shot和5-way5-shot任务中获得了较好的分类准确率。

1 算法

1.1 问题定义

小样本分类任务的目的是在每个类提供较少样本时训练分类器。每个小样本分类任务(T)都包含一个输入标签对的支持集(S)和一个未标记标签对的查询集(Q)。假设训练集一共有C类，随机抽取N类，并从N类中任意抽取K个不同样本，则称该问题为N-wayK-shot。更具体地讲，在元学习每轮训练中，N-wayK-shot问题的训练和测试任务都如下：T=S∪Q，其中S={(x1，y1)，(x2，y2)，…，(xN×K，yN×K)}，Q={(xN×K+1，yN×K+1)，(xN×K+2，yN×K+2)，…，(xN×K+q，yN×K+q)}。q是查询样本的数量，而xi和yi⊂{C1，C2，…，Cn}=CT⊂C，其中C是训练集或测试集中所有类的集合。在训练阶段，提供标签给支持集和查询集进行训练。在测试阶段时，给出测试数据Dtest，目的是训练出一个较好的分类器，该分类器能够在S⊂Dtest时，用少量的支持样本将查询样本Q⊂Dtest映射到正确的标签上，实现准确分类。其中，训练集和测试集的标签空间是互斥的，即Ctrain∩Ctest=∅。

1.2 融合分布图网络框架

本研究提出了基于小样本学习的融合分布图网络框架(Fusion Distribution Graph Network，FDGN)，如图1所示。该框架包括融合模块和分布模块，融合模块用于构建样本相关性矩阵和类间相关性矩阵，分布模块用于重构特征分布信息。

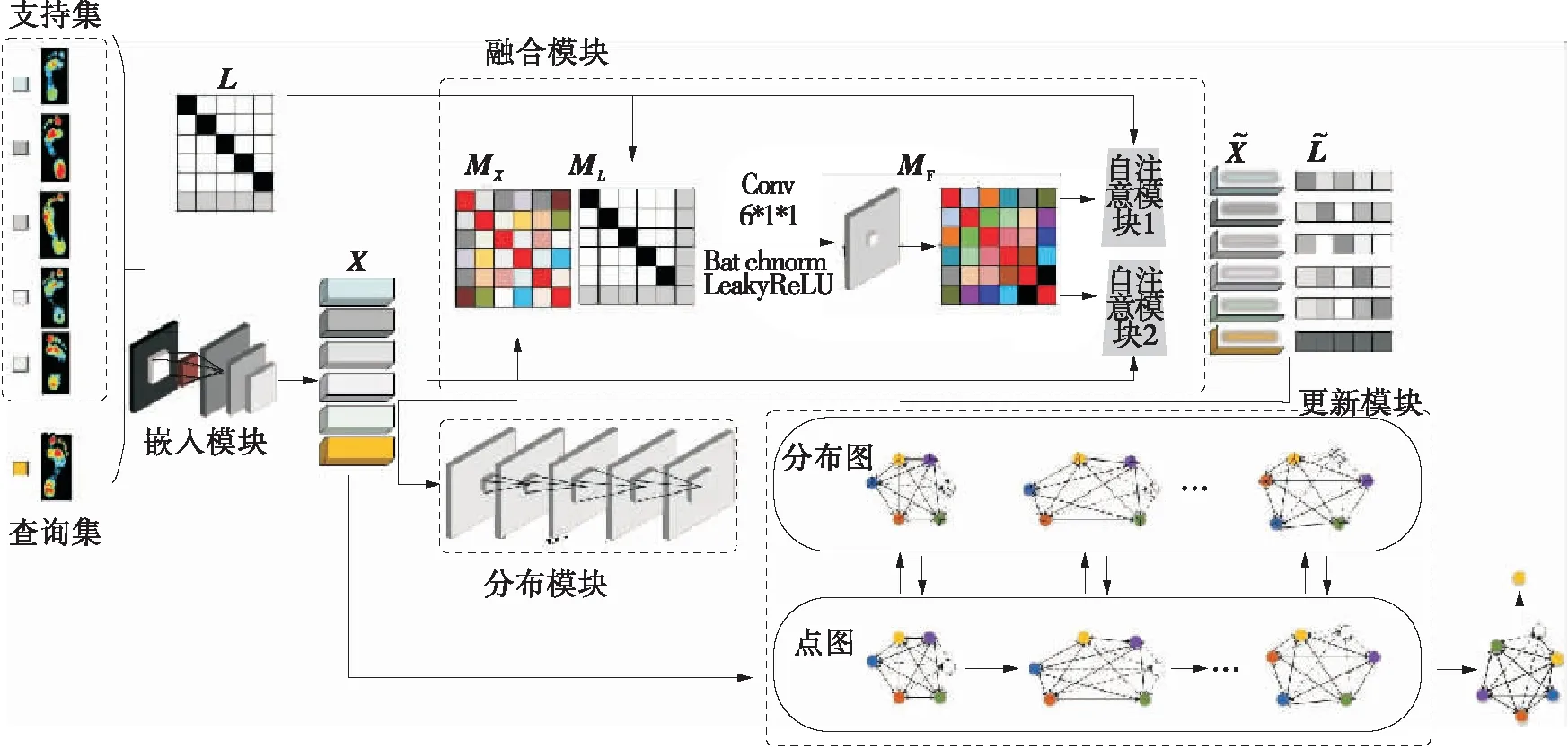
图1 FDGN的5-way1-shot总体框架Fig.1 5-way1-shot framework of FDGN

1.2.1 初始化设置

对于FDGN的每一个任务T，令G=(V，E)来构建一个全连接图，其中V是节点的集合，可以表示成V：={vi}i=1，2，…，A，E是边特征的集合，可以表示成E：={Eij}i， j=1，2，…，A，i和j表示样本编号，A是每次任务T的样本总数，也就是A=N·K+Q(Q是查询集)，图网络中图的构建示意图如图2所示。本研究预测的不是节点信息，而是边信息，因此提供的基准真值标签也不再是标签，而是真值边标签，即

(1)

其中yi和yj表示样本标签。

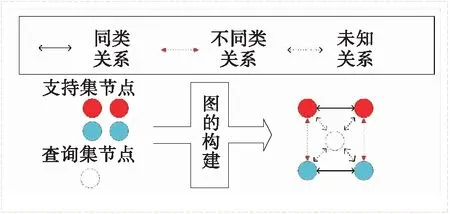
图2 2-way2-shot图模型Fig.2 A graph model in 2-way2-shot

在点图P和分布图D中，图的初始边特征e0采用基准真值边特征进行初始化，即

(2)

(3)

其中x、femb、Wemb分别代表任务样本数、嵌入网络和嵌入网络参数集。

1.2.2 相关性矩阵融合模块

本研究通过类间和样本间的相关性进行特征信息融合，以构造更具有相关性的特征信息。其中样本间矩阵MX和类间相关性矩阵ML，分别为：

MX=softmax(XXT)

(4)

ML=softmax(LLT)

(5)

MF=Conv1*1(MX‖ML)

(6)

(7)

(8)

其中，Conv代表卷积块，β取值范围为[0，1]。

1.2.3 特征重分布模块

点图中建立了样本间关系，而分布模块中特征向量描述样本在每类中分配的相对重要程度。本研究依据标签分布学习规则将一个样本的分布级别关系建模到所有其他样本，并且每个特征向量对所有样本的分布程度总和为1。

(9)

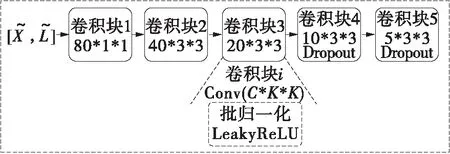
图3 分布模块的具体设置Fig.3 Detailed setting of distribution module

其中，‖代表串联操作，φd代表分布模块网络。所有卷积块都有批一化操作和LeakyReLU激活函数，为了缓解过拟合，在卷积块4和卷积块5中引入了Dropout层。

1.3 目标函数和损失函数

(10)

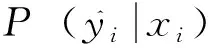
根据双图网络，损失函数则同时包含点图和分布图损失以获得更好的收敛效果，即

(11)

(12)

(13)

其中，LCE是交叉熵损失，yi是样本i的基准真值标签。

1.4 前向更新模块

前向更新模块采用双图结构实现更新，具体过程如下所示。

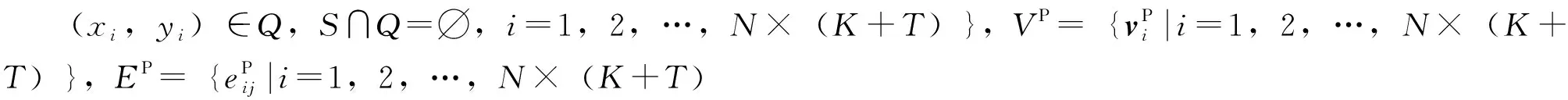
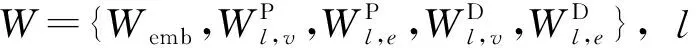
1.点图边特征更新：

2.分布图节点特征更新：

3.分布图边特征更新：

4.点图边特征更新：

2 实验及分析

本研究先在Mini-Imagenet和Tiered-Imagenet小样本数据集上验证算法的有效性。然后，针对触觉压力足迹集的特点对网络参数进行微调，验证了FDGN在足迹分类的有效性；同时探讨了超参数β对触觉压力足迹数据集实验结果的影响。

2.1 Mini-Imagenet和Tiered-Imagenet实验

2.1.1 数据集

Mini-ImageNet数据集[21]总共有100类，是ILSVRC- 12的子集[22]，例如打印机、藏獒、指示牌、陶瓷碗等。每个类有600张图像，均为84×84的RGB图像。本研究按照64、16、20类分别用于训练、验证和测试[23]。

Tiered-ImageNet数据集[24]与Mini-Imagenet数据集[21]类似，是ILSVRC- 12的子集[22]，总共有608类，其中每个类别都属于从Imagenet高层节点中抽取的34个高层类别中的一个。每个较高级别的类别包括10到20个类，分为20个类(351个子类)6个验证集(97个子类)和8个测试集(160个子类)类别。每个类的平均图像数量为 1 281 张，见表1。

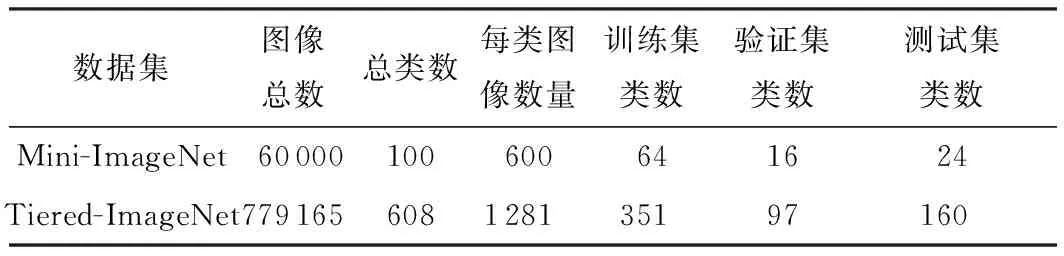
表1 Mini-Imagenet和Tiered-Imagenet数据集具体设置Table 1 Detailed settings of Mini-Imagenet and Tiered-Imagenet datasets

2.1.2 实验结果与分析

本研究在数据处理方面按照文献[25- 26]提到的基本设置，如图像亮度对比度调整、图像中心随机裁剪和水平翻转。5-way1-shot在每轮的批数设为25。所有实验中全部采用Adam优化器，初始学习率设置为10-3，并且每17 000轮学习率降低0.1个百分点，权重衰减率设置为10-5，总迭代次数为10万次。本文结果采用每1 000轮的平均准确率表示。

为验证本研究方法的优越性，进行了关系网络(RN)[27]等6个基于ConvNet嵌入网络的小样本学习算法，以及DPGN[15]等4个基于ResNet12嵌入网络的图网络小样本学习算法下的5-way1-shot任务进行比较。其中ConvNet主要由4个Conv-BN-REU模块组成，最后两个模块还包含Droput层以缓解过拟合[28]。ResNet12与文献[29]中描述的相同，主要有4个块，其中有一个用于ResNet12的残留块。所有嵌入网络的最后卷积特征由全局平均池化处理，然后是具有批归一化的全连接层[30]，以获得128维特征嵌入。

如表2所示，嵌入网络采用ConvNet时，本研究提出的算法分别与TPN[31]、ProtoNet[32]、RN[27]、MAML[33]、EGNN[14]、DPGN[15]进行比较，其中传统小样本算法TPN[31]在Mini-Imagenet和Tiered-Imagenet 数据集下5-way1-shot任务的准确率分别是55.51%和59.91%，而本研究提出的算法的准确率分别为71.44%和70.40%，准确率有了大幅度的提升。基于图网络的小样学习算法DPGN[15]在Mini-Imagenet和Tiered-Imagenet数据集下5-way1-shot任务的准确率分别是66.01%和69.43%，本研究基于分布融合的图网络使得准确率分别提升了5.43和0.97个百分点。

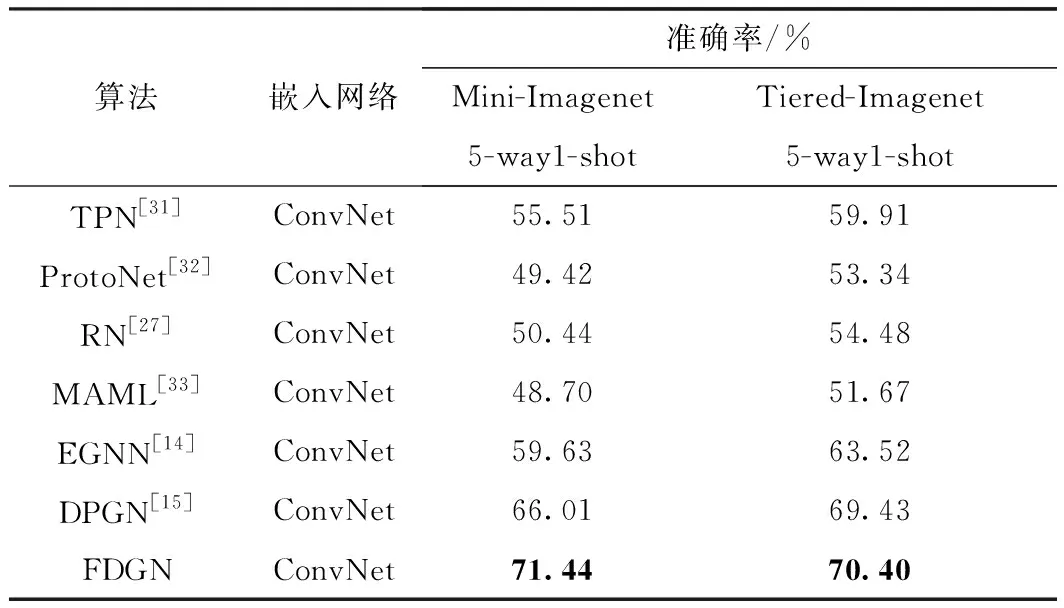
表2 基于ConvNet嵌入模块的算法分类准确率Table 2 Classification accuracy of embedded module based on ConvNet

嵌入网络采用ResNet12，将本研究提出的算法分别与Shot-Free[34]、Meta-Transfer[35]、MetaOptNET[36]、DPGN[15]进行比较，结果见表3。其中本研究在Mini-Imagenet和Tiered-Imagenet数据集下5-way1-shot任务的准确率分别是71.71%和74.34%，较传统小样本算法MetaOptNET[36]的准确率分别提升了9.07和8.53个百分点，同时较基于图网络小样学习算法DPGN[15]的准确率分别提升了3.94和1.89个百分点。因此本研究提出的算法在不同嵌入网络中都达到了较好的实验结果。

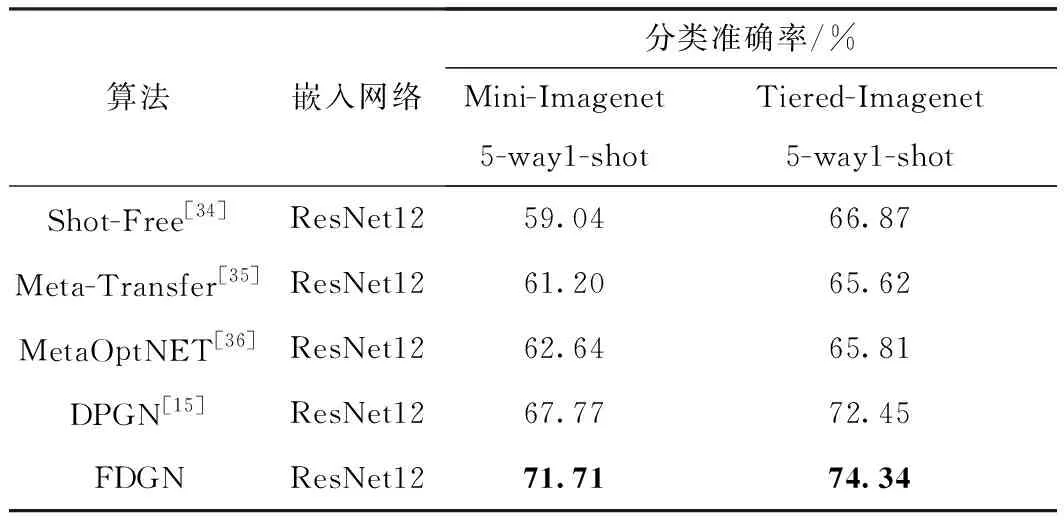
表3 基于ResNet12嵌入模块的算法分类准确率Table 3 Classification accuracy of embedded module based on ResNet12

表4中任务方式采用5-way1-shot，讨论了不同层数下图卷积聚合邻域信息能力对实验结果的影响，其中l代表图卷积的层数。实验表明，当层数较浅时，经过的点图和分布图的交替更新次数不能很好地将标签信息从带标签的样本传播到未带标签的样本中，并且在更新时因层数较浅导致节点聚合邻域信息时不能准确记住重要且独特的信息。而当层数较深时，会不可避免地遭遇图网络的过平滑问题[37]，从而使节点过度混合邻域信息，造成信息冗余，导致性能下降。因此在本实验中l为6时得到了最好结果。

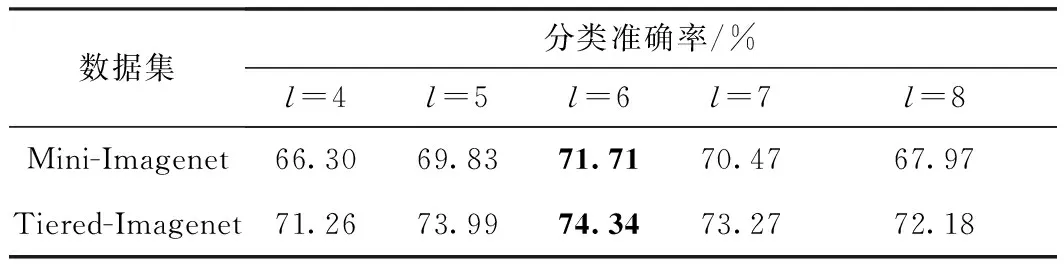
表4 不同网络层数的分类准确率Table 4 Classification accuracy of different network layers

2.2 触觉压力足迹实验

2.2.1 数据集

触觉压力足迹数据集依托公安部物证鉴定中心和安徽大学共建的足迹感知与分析实验室采集构建。该数据集包含137位正常成年人足迹数据，每位对象左、右足分别站立在压力采集板上采集10次，其中每个对象有左、右足各10张足迹图像。由于少数人站姿不规范，10张图像中少数存在倾斜和缺失情况，如图4所示。由于数据采集过程中会因硬件的原因产生噪声，如数据线、电阻元器件等硬件，所以数据均经过手动处理噪声且经过标准化处理。

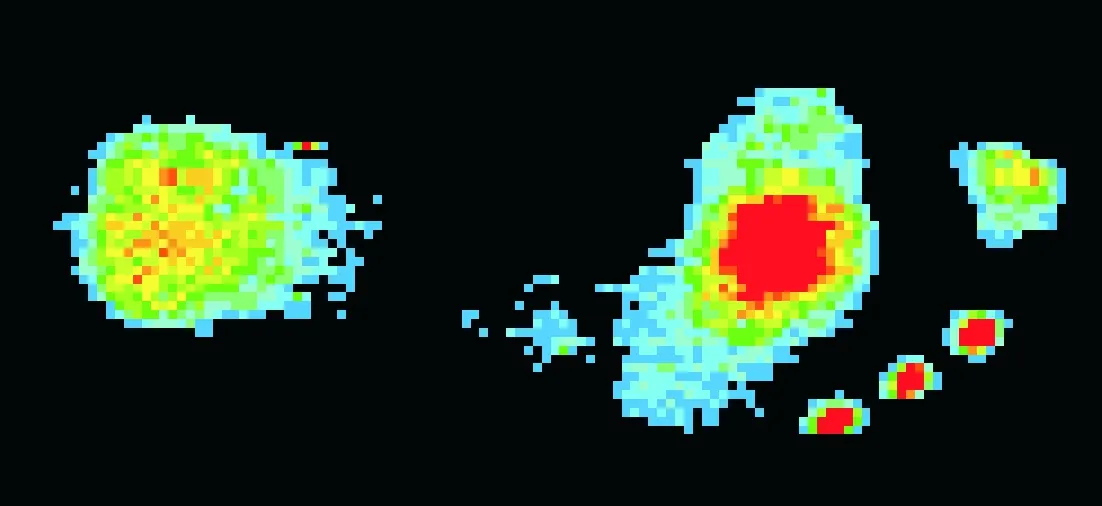
(a)右足

(b)左足

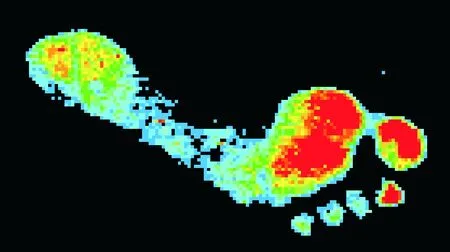
(c)倾斜右足

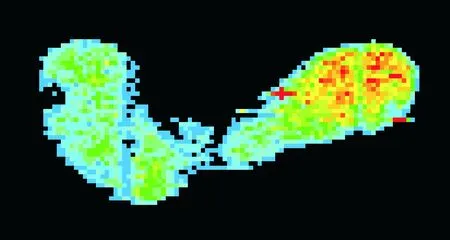
(d)残缺左足图4 触觉压力足迹数据Fig.4 Tactile pressure footprint data

本研究中触觉压力足迹数据集分为3个触觉压力足迹数据子集，分别为左右足数据集(Foot_all)、左足数据集(Foot_left)、右足数据集(Foot_right)，数据集的具体构建见表5。

表5 触觉压力足迹数据集具体信息Table 5 Detailed information of pressure footprint of tactile pressure footprint data set

2.2.2 实验结果与分析

5-way1-shot和5-way5-shot实验过程中，本研究的训练集、验证集、测试集均以137人的数据集按照117：10：10的比例进行划分，所有触觉压力足迹图像的尺寸大小均改成84×84，并用传统的数据增强方法[25- 26]，如图像的水平翻转、图像中心随机裁剪和图像亮度对比度调整。本研究在基于触觉压力足迹数据集上的实验网络层数l选择为6。

为验证本研究提出的算法在触觉压力足迹数据上的有效性，分别在ConvNet和ResNet12为嵌入网络的小样本学习算法中进行比较。如表6所示，在嵌入网络采用ConvNet时，本研究提出的算法在3个触觉压力足迹数据子集上基于5-way1-shot和5-way5-shot任务下都取得了不错的效果。在Foot_all数据集的5-way1-shot任务中，本研究的准确率是88.87%，较传统小样本算法RN[27]和基于图网络的小样本算法DPGN[15]分别提升了12.04和1.92个百分点。在Foot_left数据集5-way1-shot任务中，本研究的准确率是83.91%，较传统小样本算法RN[27]和基于图网络的小样本算法DPGN[15]分别提升了13.76和0.89个百分点。在Foot_all数据集的5-way5-shot任务中，本研究的准确率是97.79%，较RN[27]和DPGN[15]分别提升了3.30和0.94个百分点。

在嵌入网络采用ResNet12时，本文算法同样也取得了较好的结果。在Foot_all数据集的5-way1-shot任务中，较传统小样本算法RN[27]和基于图网络的小样本算法DPGN[15]分别提升了7.00和2.17个百分点。在Foot_left数据集的5-way1-shot任务中，较传统小样本算法H-Protonet[38]和基于图网络的小样本算法DPGN[15]分别提升了7.29和2.03个百分点。在Foot_all数据集的5-way5-shot任务中，本研究的准确率是98.66%，较H-Protonet[38]和DPGN[15]分别提升了8.34和0.41个百分点。在Foot_right数据集的5-way1-shot和5-way5-shot任务中更是分别达到了90.45%和98.96%。

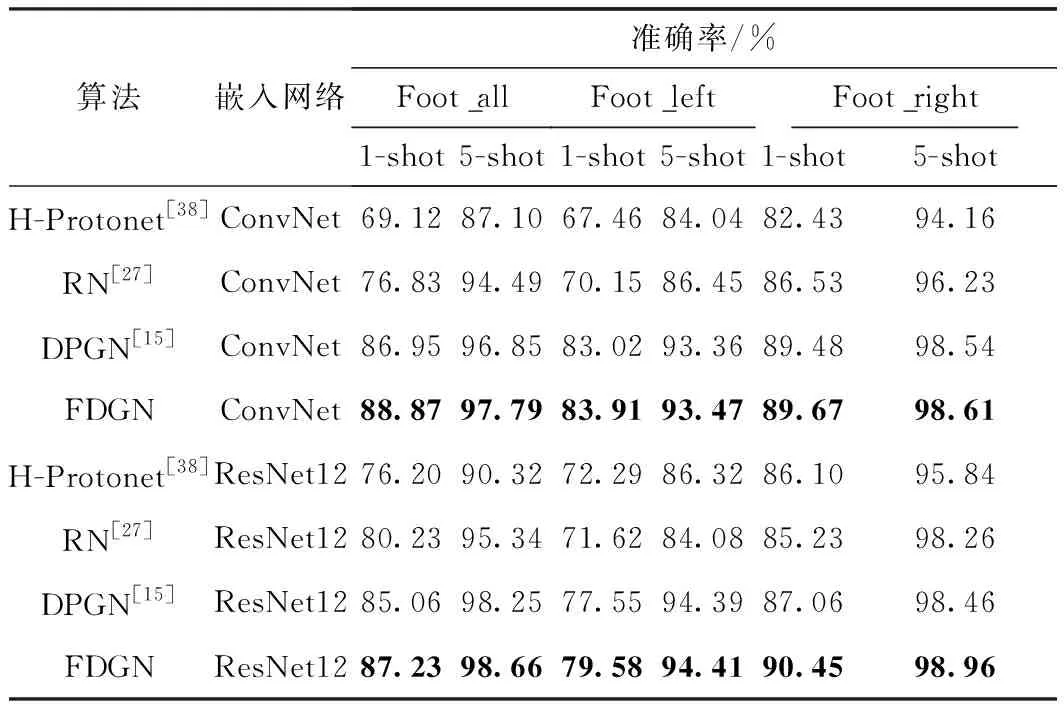
表6 基于5-wayN-shot任务在触觉压力足迹数据集上的准确率Table 6 Accuracy of 5-wayN-shot task on tactile footprint pressure data set

由表6可知，测试Foot_left数据集的准确率低于Foot_all数据集。分析数据集得知，Foot_left数据集的采集会被仪器灵敏度和被采对象动作不规范等因素干扰，导致Foot_left数据集中存在部分残缺图片(如图4(d)所示)，对网络提取重要且独特的压力特征造成了一定的干扰，使得准确率下降。不过，本研究提出的方法与其他模型比较，仍取得了不错的实验结果。

由表2、表3和表6可知，FDGN不仅在小样本公共数据集上表现优越，而且在由足迹感知与分析实验室采集的触觉压力足迹数据集上也得到不错的效果。由此说明本研究所提出的改进对于分类能够具有一定提升。并且多个数据集的结果显示本研究所提出的模型相较与原模型结果都有提升，进一步说明本研究提出的模型具有一定的可适用性和鲁棒性。

2.3 消融实验

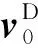
如图5所示，不同的β值对实验结果存在一定的影响。当取值稍小时，使得初始标签one-shot向量趋于0，对计算自注意模块的权重系数产生一定的干扰，同化了分布模块的权重分配。当β取值较大时，自注意模块中初始表达特征比重过大，在分布模块中一定程度上弱化了相关性矩阵信息，导致卷积特征表达能力下降，影响样本特征在被分配时的重要程度。因此本文中β取0.5。

图5 基于5-way1-shot上不同β的准确率Fig.5 Accuracy of 5-way1-shot task on different β

本文的分布图节点特征vD经过重新设计取得了不错的实验结果。对于本文提出的融合相关性矩阵和分布模块对构建vD的影响，实验结果表明，加入样本相关性矩阵和类间相关性矩阵后实验分类准确率分别达到了68.41%和68.84%，较初始模型DPGN算法[15]分别提升了0.64和1.07个百分点，这说明由正则范数化生成的相关性矩阵拥有更好的卷积特征表达能力。分布模块中未用融合相关性矩阵时准确率是68.57%，较DPGN提升了0.80个百分点，当考虑到融合相关性矩阵时准确率提升至69.41%。从以上分析可知，融合相关性矩阵和分布模块对模型准确度有一定的提升。

3 结语

本研究在重构分布图节点特征上提出了一个基于小样本学习的融合分布图网络，即首先通过融合相关矩阵获得卷积特征信息，然后由自注意模块来丰富特征信息，最后经分布模块按照标签学习准则重分配分布图的节点特征，网络在更新时明确地结合了样本级和分布级的关系。大量的实验表明，本研究提出的方法在小样本学习公共数据集上获得了不错的结果，基于5-way1-shot的实验结果在Mini-Imagenet、Tiered-Imagenet数据集上分别达到71.71%和74.34%。同时在3个触觉压力足迹数据集上获得了较好的分类准确率，其中在触觉压力左右足数据集上5-way1-shot和5-way5-shot的实验结果分别达到88.87%和98.66%，在触觉压力右足数据集上的5-way1-shot和5-way5-shot实验分别达到90.45%和98.96%。在接下来的研究中，应进一步挖掘触觉压力足迹的类间差异和类内差异，并尝试图神经网络中边特征的不同聚合方式，以提高足迹特征表达能力，从而获得性能更好的网络模型。