基于蠕变理论的自锚式悬索桥索夹预紧力研究
2022-02-21唐冕车天鑫宋旭明胡省阳
唐冕 车天鑫 宋旭明 胡省阳
(中南大学 土木工程学院,湖南 长沙 410075)
自锚式悬索桥主缆与地锚式悬索桥主缆相比存在跨径小、垂跨比大及直径小的特点,通过索夹与吊杆的连接,主缆和桥塔构成了自锚式悬索桥的主要承力结构,保证了桥梁结构安全和稳定。因此主缆与索夹锚固系统在设计上必须保证施工过程和运营阶段的可靠性。
影响主缆与索夹锚固系统安全的影响因素主要有以下几点:①主缆与索夹界面抗滑稳定性;②连接部件结构强度;③主缆的倾角大小;④运营阶段高强螺栓预紧力的损失。随着近年来自锚式悬索桥运营时间的增加,主缆与索夹锚固系统安全分析愈发重要。而索夹的空间稳定性主要是依靠高强螺栓的预紧力产生索夹与主缆的接触压力,通过索夹与主缆表层钢丝的摩擦机制使索夹牢固约束主缆,因此预紧力的大小是索夹空间稳定性的重要影响因素。主缆在长期的拉力作用下,随时间增长而增加的变形(即蠕变)以及高强螺栓应力松弛现象对于预紧力都有一定的影响。
目前,国内外研究学者对高强钢丝应力松弛以及螺栓预紧力的损失进行了大量的研究。杨富强[1]利用蠕变模型计算裂尖蠕变,将蠕变模型表示为应力、时间与温度的函数εcr=f1(σ)f2(t)·f3(T),其中f1(σ)、f2(t) 、f3(T)分别表示为应力、时间和温度的函数。基于该模型选取双曲正弦形式的应力函数,精确地模拟了材料的蠕变行为。刘俊等[2]分析了预应力圆弧螺纹锚栓常温应力松弛和蠕变行为,通过试验得到了不同初始荷载下锚栓应力-时间关系曲线和锚栓的蠕变-时间曲线,研究表明预应力圆弧螺纹锚栓常温下的应力松弛和蠕变在前5h内迅速增加,随后趋于稳定。赵越[3]以成桥阶段悬索桥主缆为研究对象,将主缆材料理想化为各向同性材料,分析了主缆泊松效应对主缆缠丝力及索夹高强螺栓预紧力的影响,推导出施工阶段由于吊索力施加导致主缆截面径向收缩引起的索夹高强螺栓预紧力损失计算公式。张鹏飞、周伟等[4- 5]认为悬索桥索夹螺杆预紧力损失的主要原因是:①钢丝蠕变导致了螺杆预紧力损失;②螺栓材料的时效松弛;③荷载变化使主缆内钢丝排列变化及主缆孔隙率变小。
目前很少有学者考虑金属蠕变及螺栓松弛对预紧力损失造成的影响。为此,本研究将基于时间硬化金属蠕变(松弛)模型理论,建立主缆索夹一体模型探究自锚式悬索桥主缆与索夹锚固系统中由蠕变(松弛)引起的高强螺栓预紧力损失机理。
1 基本原理
1.1 蠕变与应力松弛关系
蠕变和应力松弛是粘弹性材料在长期荷载作用下的一种固有力学行为,可以视作一种物理现象的不同表现形式。假设试件在拉伸载荷作用下的初始应力小于屈服极限,构件的总变形可表示为式(1),试件的应力应变关系表示为式(2):
ε=εe+εcr
(1)
dεcr/dt=-dεe/dt=-(dσ/dt)/E
(2)
其中:εe表示弹性变形,εcr表示蠕变变形,σ表示应力,E表示材料弹模,t表示时间。
在试件蠕变试验中,随着加载时间的增加,ε在外荷载的作用下不断发展,但由于应力保持不变,即弹性变形保持不变,此时只有蠕变变形在发展。在试件松弛试验中,总变形保持不变,随着加载时间的增加,试件蠕变变形依然不断发展,造成弹性变形逐渐减小,从而引起应力减小,而弹性变形减小的部分则转化成蠕变变形。
于是,若把松弛看作由无数个微小时间单元内恒应力蠕变过程的组合,则应力松弛实际上即是蠕变的一种特殊形式,即变应力下的蠕变。另一方面,若把蠕变看作由无数个微小时间单元内恒应变松弛过程的组合,则蠕变实际上是应力松弛的一种特殊形式,即变应变下的松弛[6]。
1.2 时间硬化蠕变(松弛)模型
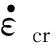
(3)
时间硬化蠕变模型应变速率则可表示为[9]
(4)
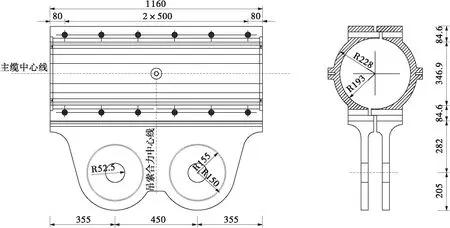
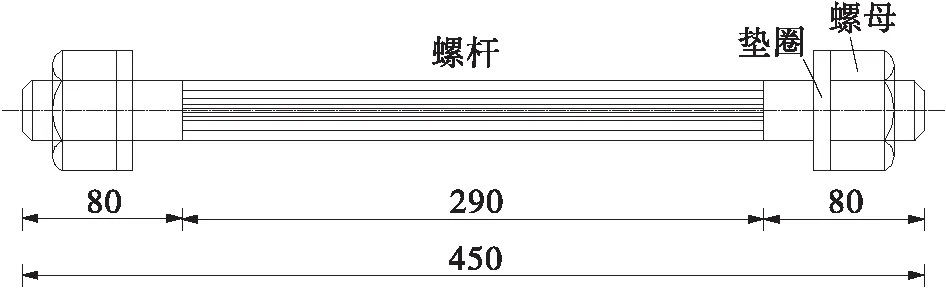
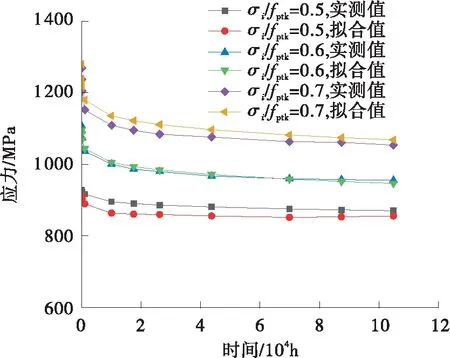
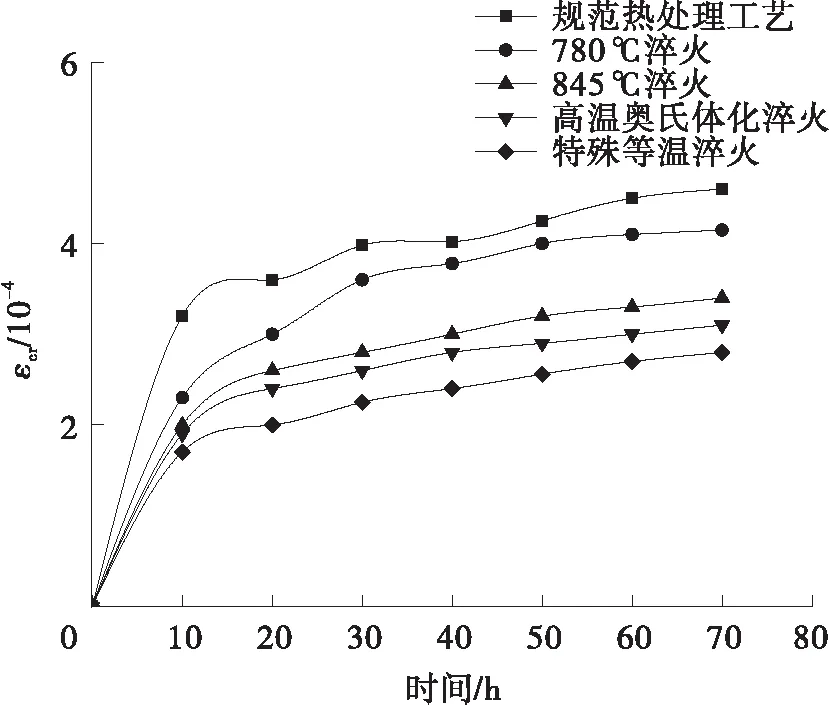
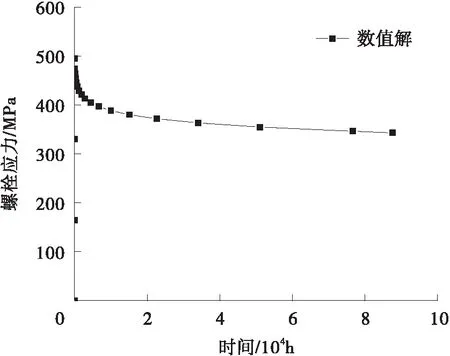
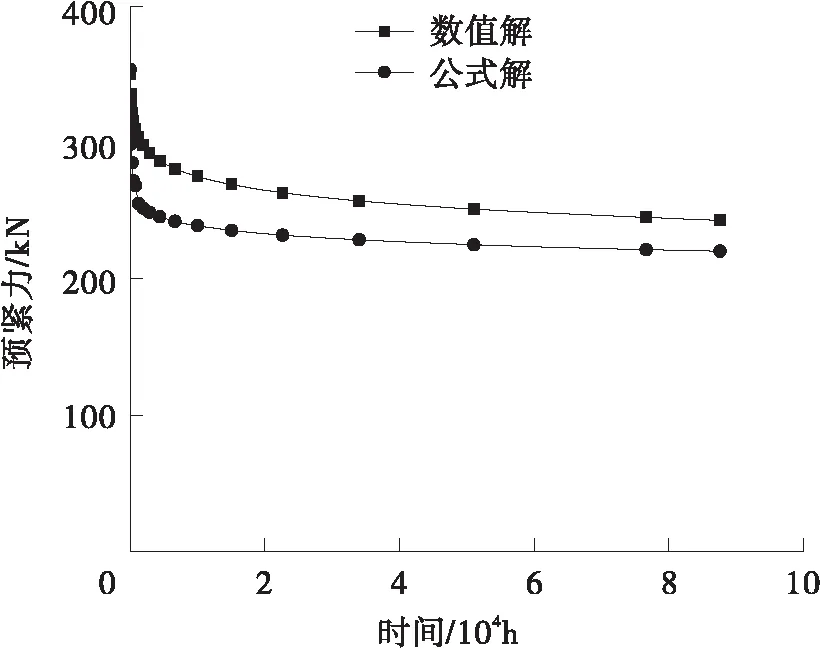
其中,A、m、n为材料常数,且0 回代到式(2)中,可得 B(t)σn=-(dσ/dt)/E (5) 设定初始条件t=0,σ=σi,积分可得 (6) 式中,σi为初始应力,t为蠕变松弛时间,σ为剩余应力。 再对式(4)进行讨论,有 B(t)=Amtm-1 (7) (8) 图1 B(t)与Ω(t)函数关系图Fig.1 Functional diagram of B(t)and Ω(t) 因此本文在时间硬化蠕变模型理论的基础上对自锚式悬索桥主缆与索夹锚固系统因蠕变松弛产生的预紧力损失现象开展研究,并探讨预紧力损失发展规律。 本研究选取长沙三汊矶湘江大桥,桥型为大跨度自锚式悬索桥,选择其主缆索夹作为本研究的对象。 (1)主缆构造 为保证桥梁结构横向稳定性,全桥共设两根由37股预制束股挤压成型的主缆,每束股由127根 标准强度为1 600 MPa的镀锌高强钢丝组成,主缆空隙率索夹内为18%,索夹外为20%,主缆直径为390 mm。 (2)索夹铸件 索夹采用左右对合、销接带耳板的形式,两片索夹用高强螺栓夹紧,如图2所示。索夹采用ZG270- 500铸钢铸造。 图2 索夹构造图(单位:mm)Fig.2 Structural drawing of cable clamp(Unit:mm) (3)M30高强螺栓 索夹螺栓采用缩腰形,长度为450 mm,螺杆在吊索索夹上的顺桥向间距为200~300 mm,其构造如图3所示。索夹螺杆、螺母及垫圈材料分别为40CrNiMoA、15MnVB和40Cr。 图3 M30高强螺栓构造图(单位:mm)Fig.3 Structural drawing of M30 high strength bolt(Unit:mm) 2.2.1 主缆等效材料 自锚式悬索桥主缆较地锚式悬索桥主缆截面直径小,在高强螺栓预紧施工过程中,主缆材料表现出较为明显的非线性特征,基于各种有限元软件虽然能够准确地模拟主缆精细化有限元模型,但是往往工作量和计算量巨大。 为简化计算,基于均质化思想,主缆采用了文献[10]提出的柱坐标系下的三项异性均匀等效材料模拟[10],以主缆圆心为坐标原点,建立如图4所示空间柱坐标系来表征等效主缆各向异性材料受力特性。沿Z轴主缆材料承受拉应力,材料主要表现为高强钢丝材料特性,径向R主要传递相邻钢丝层间压力,θ方向主要传递层间摩擦以及同层钢丝之间的挤压作用。其3个方向的材料弹性模量分别为EZZ=1.95×105MPa,ERR=2.2×104MPa,Eθθ=3.6×104MPa;3个方向材料泊松比分别为νZR=0.26,νZθ=0.26,νRθ=0.02。 图4 主缆等效材料模型Fig.4 Equivalent material model of main cable 严琨[11]通过试验与有限元计算对比发现,悬索实测位移数据介于大刚度梁单元与小刚度梁单元的计算值之间,且与大刚度梁单元的计算值的误差更小,因此可以认定鞍座及索夹部位的主缆抗弯刚度接近主缆整体截面抗弯刚度。 2.2.2 模型建立 本节以接触有限元分析理论为基础,利用ANSYS软件建立考虑整体截面抗弯刚度的三向异性等效材料主缆与索夹接触有限元实体模型。 主缆-索夹锚固系统空间受力行为的特点是索夹在高强螺栓的预紧力作用下挤压主缆,通过索夹与主缆表层钢丝的摩擦机制使索夹牢固约束主缆,保持主缆-索夹锚固系统在吊索力荷载作用下的稳定。在对主缆与索夹进行有限元分析时,高强螺栓预紧力采用PRETS179预紧单元模拟,预紧方式分三级预紧,一级预紧荷载100 kN、二级预紧荷载100 kN和三级预紧荷载155 kN,三级预紧加载完毕,每根高强螺栓预紧力达到355 kN。 根据主缆等效三向异性材料模型,拟采用SOLID95单元模拟主缆、索夹及高强螺栓实体。SOLID95单元为3D20节点结构实体单元,该单元由于采用协调的位移插值函数,能更好地拟合不规则边界,单元模型如图5所示;且主缆单元划分坐标系定义为柱坐标系,以表现等效材料的三向异性。 图5 SOLID95单元Fig.5 SOLID95 unit 在ANSYS中,仿真两个弹性体之间的接触主要是通过在目标面单元和接触面单元创建接触对实现的。本文的工程背景中,主缆-索夹锚固系统之间的接触类型有两种,即刚-柔接触及柔-柔接触,高强螺栓与索夹的接触表面刚度比较接近,属于柔-柔接触。采用接触单元CONTA174和目标单元TARGE170单元创建接触对[12]。主缆与索夹的接触面的径向刚度相差较大,属于刚-柔接触类型,设置主缆表面为柔性接触面,接触单元采用CONTA174单元,索夹内侧面为目标面,目标单元采用TARGE170单元。接触单元的摩擦系数按规范[13]取0.15,接触算法采用增广拉格朗日算法。最终,建立主缆-索夹锚固系统实体有限元模型如图6所示。 图6 高强螺栓预紧力损失整体有限元模型Fig.6 Overall finite element model of pre-tightening force loss of high strength bolt 蠕变模型常数一般是由蠕变资料确定,根据时间硬化模型可知,在得到初始应力及蠕变发生一段时间后的残余应力,运用高强钢丝的松弛试验数据并利用Origin软件对式(6)进行非线性回归分析[14],最终得到拟合参数A、n、m。 对文献[15]高强钢丝松弛试验数据进行多元非线性回归分析得出蠕变(松弛)模型常数A为1.29×10-7,n为0.717 65,m为0.191 69。将拟合参数A、n、m的值回代入式(6),即可得到不同初始应力条件下所计算的松弛残余应力;其与试验所观测数据对比见图7,二者误差较小,拟合参数计算精度良好。图中fptk表示高强钢丝的抗拉极限强度。 图7 主缆蠕变模型参数A、n、m拟合精度Fig.7 Fitting accuracy of creep model parameters A,n and m of main cable 取出主缆局部节段进行分析,文献[11]中对主缆的轴向拉伸试验数据表明,主缆的轴向力学指标与高强钢丝的力学指标一致,并且在主缆较大的轴力作用下,主缆截面拉应力呈不均匀特点,即下缘大上缘小、中间层表现出类似中性层的特点。故在分析主缆蠕变时,可视为仅仅承受拉应力荷载,等效为主缆截面的一维蠕变分析。模型中采用SOLID95实体单元,其能够有效地模拟材料塑性、超弹、黏弹、黏塑、蠕变等状态。边界条件设置一端固结,一端施加轴向拉力。根据计算,主缆高强钢丝为I级松弛钢丝的最大设计值为1 033 MPa,II级松弛钢丝的最大设计值为956 MPa。根据最大设计值设置了7个等级的轴向拉应力,并基于时间硬化蠕变模型,代入非线性回归分析得到的蠕变模型常数A、n、m,分别计算各工况下主缆的蠕变随时间的变化量,结果见表1。 表1 各级工况下主缆蠕变随时间变化值Table 1 Creep variation of main cable with time under various working conditions 根据表1各级加载工况下蠕变与时间和初始应力σ0的关系,利用Matlab软件,拟合二维曲面函数,该函数的自变量为时间t和初始应力σ0,因变量为主缆的蠕应变,拟合的函数见式(9)。 εcrc=a+bln(gσ0)+clnt+dσ0t-0.2+et-0.5 (9) 式中,εcrc为主缆轴向蠕变,σ0为主缆轴向初始应力。a、b、c、d、e、g为常数,其值分别为: a=-0.003 958,b=0.000 370 3,c=5.983×10-5,d=-8.964×10-6,e=0.289 3,g=10.2。 为验证该公式的拟合精度,分别取3个加载工况初始应力σ0分别为400、700、1 000 MPa的数值解与拟合公式解进行对比分析,如图8所示。可知式(9)的计算值与ANSYS有限元计算的数值解十分接近,数值解与公式解的最大误差仅为4%,可满足工程精度的需要。 (a)初始应力为400 MPa (b)初始应力为700 MPa (c)初始应力为1 000 MPa图8 不同初始应力时主缆蠕变数值解与公式解对比Fig.8 Comparison between numerical solution and formula solution of main cable creep under different initial stress 40CrNiMoA钢是合金结构钢的一种,具有较高的强度、韧度和良好的淬透性和抗过热的稳定性,常作为高强零件如齿轮、轴类及紧固件等。 刘云旭等[16]通过常温蠕变试验研究了不同热处理工艺强化后的40CrNiMoA钢在低于屈服强度的应力作用下的常温蠕变行为和影响因素。 试验加载的应力为抗拉强度标准值的0.5倍,40CrNiMoA钢试件经不同热处理工艺后的常温蠕变曲线如图9所示。 图9 初始应力比为0.5时40CrNiMoA钢常温蠕变曲线Fig.9 Room temperature creep curves of 40CrNiMoA steel with an initial stress ratio of 0.5 在本研究工程背景中的高强螺栓的预紧荷载为355 kN,平均应力为502 MPa,高强螺栓材料为10.9级,因此在接下来的高强螺栓蠕变分析可采用该应力比下的蠕变试验数据开展。 在得出40CrNiMoA钢试件的常温蠕应变与时间相关的数据后,进行多元非线性回归分析得出40CrNiMoA钢蠕变模型的3个常数A、n、m,A为1.548 39×10-6,n为0.931 08,m为0.078 47。 为简化分析,单独建立高强螺栓有限元模型,模型中采用SOLID95结构实体单元,边界条件设置为两端固结,初始应力采用预紧力的方式施加,一次加载至355 kN。 计算得出蠕应变随时间的发展趋势的数值解,与试验资料的对比结果见图10。可知二者最大误差为3.7%,可满足工程精度要求。 图10 40CrNiMoA钢蠕变模型参数A、n、m拟合精度Fig.10 Fitting accuracy of creep model parameters A,n and m of 40CrNiMoA steel 常温下基于时间硬化模型得到的高强螺栓应力随时间变化的曲线如图11所示。从计算结果看,高强预紧螺栓在初期预紧力施加后,应力水平增加至峰值495.159 MPa,随后高强螺栓发生材料的蠕变,进入应力松弛阶段,在初始10 000 h(约1.1年)以内,高强螺栓的应力迅速下降至388.875 MPa。随后应力下降趋势变缓。在应力松弛发生10年以后,最终应力下降至343.235 MPa。分析可知,在应力松弛现象发展前10 000 h以内,螺栓的应力已经下降了约总体损失的70%,随后时间内(约为8.9年)螺栓应力下降了约总体损失的30%。可看出,高强螺栓的应力松弛在初期很快,随后步入缓慢下降的阶段,在第10年下降约2 MPa,可说明10年以后应力松弛现象已经十分不明显。 图11 40CrNiMoA钢螺栓应力松弛曲线Fig.11 Stress relaxation curve of 40CrNiMoA steel bolt 在得出高强螺栓截面应力以后,可通过应力在截面上积分得出螺栓截面上的预紧力Pb数值解随时间发展的曲线。根据基于时间硬化模型的应力松弛公式(6),代入常数A、n、m后可得出一段时间后高强螺栓截面的松弛残余应力,通过在截面上的积分可得到预紧力Pb公式解随时间发展的曲线,两者对比结果如图12所示。数值解与公式解的发展趋势保持一致,在松弛前期,预紧力迅速下降,在前10 000 h(约1.1年)以内,预紧力由355 kN迅速下降,数值解下降至约270 kN,公式解下降至约240 kN。随后预紧力下降速率放缓,在第10年,数值解仅下降了约为2 kN,公式解仅下降了约为1.1 kN。最终有限元计算的预紧力损失为112.38 kN,公式计算的预紧力损失为139.78 kN,二者计算存在一定的误差,但这部分与公式计算的预紧力损失偏于保守有关。 图12 40CrNiMoA钢螺栓预紧力松弛曲线Fig.12 Pre-tightening force relaxation curves of 40CrNiMoA steel bolt 主缆的蠕变导致的径向收缩以及高强螺栓的预紧力松弛是索夹预紧螺栓预紧力损失的主要原因。随着主缆蠕变的发生,主缆的径向收缩造成高强螺栓的应力弹性损失,这个过程与高强螺栓自身应力松弛行为过程是高度耦合的。因此高强螺栓各个时刻发生应力松弛的初始应力会发生双重改变,一是主缆蠕变造成的改变,二是自身应力松弛造成的减小。本节基于上两节对主缆以及螺杆的蠕变(松弛)情况的讨论,基于保守考虑得出自锚式悬索桥索夹高强预紧螺栓预紧力损失计算公式: Pl=Plc+Plb (10) 式中,Pl为单根螺杆总预紧力损失,Plc为主缆蠕变引起的单根螺杆预紧力损失,Plb为高强螺栓应力松弛引起的单根螺杆预紧力损失。 设有微小的正平行六面体,其棱边长度为Δx、Δy、Δz。在变形之前,其体积是ΔxΔyΔz,在变形之后,其体积变化为(Δx+εxΔx)(Δy+εyΔy)·(Δz+εzΔz),因此其每单位体积的体应变为 εx+εy+εz+εxεy+εyεz+εzεx+εxεyεz (11) 略去高阶微量得 θ=εx+εy+εz (12) 式中,εx、εy、εz分别为x、y、z方向的应变,θ为体应变。 根据蠕变力学基本假定,在金属材料蠕变过程中,体积仍然按照弹性规律变化,因此金属的蠕变不引起体积的变化。 (13) 以Sc 0、Lc 0分别为主缆节段在蠕变发生之前的初始截面积和初始长度,Sc、Lc为主缆节段实时面积和长度,因此根据蠕变体积不变有 Sc 0Lc 0=ScLc (14) (15) (16) 根据主缆、索夹与螺栓的变形协调条件,可得因主缆蠕变导致径向收缩引起高强螺栓的轴向应变及预紧力损失分别为 (17) (18) 式中,Eb为高强螺栓弹性模量,lb为高强螺栓预紧长度,Sb为高强螺栓横截面面积。 根据时间硬化模型得出高强螺栓的松弛残余应力为 (19) 将式(18)与式(19)代入式(10)可得考虑主缆蠕变与高强螺栓应力松弛双因素影响下高强螺栓的预紧力损失公式: (20) 式中,σb 0为高强螺栓初始应力,Ab、nb、mb为高强螺栓应力松弛模型常数。 由于自锚式悬索桥主缆与索夹锚固系统中的高强螺栓预紧力损失受众多因素影响,如主缆的初始应力、工作时间、高强螺栓的初始应力及索夹的变形等因素,而蠕变(应力松弛)模型中的相关参数与各影响参数密切相关,因此自锚式悬索桥高强螺栓的预紧力损失是一个较为复杂的过程。本研究进行简化分析,预紧力损失公式(20)基于保守角度,采用叠加法计算高强螺栓预紧力损失,仅分步考虑主缆蠕变导致径向收缩引起的高强螺栓预紧力损失与高强螺栓自身金属材料的应力松弛效应导致的预紧力损失,未考虑两者之间的相互影响。为验证该公式的可靠性,采用图6所示的高强螺栓预紧力损失整体有限元模型进行数值分析验证。 分别取3个加载工况进行有限元分析,即主缆初始应力σ0分别为400、700和1 000 MPa,高强螺栓预紧力一次加载至355 kN,经ANSYS有限元计算得到自锚式悬索桥主缆与索夹锚固系统中高强螺栓预紧力的十年损失数值解,并与按照式(20)计算的公式解对比分析,如图13所示。研究表明: (a)初始应力为400 MPa (b)初始应力为700 MPa (c)初始应力为1 000 MPa图13 不同主缆初始应力时的高强螺栓预紧力损失Fig.13 Pre-tightening force loss of high strength bolt under different initial stress of main cable (1)自锚式悬索桥主缆与索夹锚固系统高强螺栓预紧力损失公式解与数值解的发展趋势基本一致。在预紧力损失初期阶段,数值解的增长速率及其数值稍微大于公式解,误差最大为20 kN左右,在约10 000 h以后,公式解会偏大于数值解,并在预紧力损失发展10年后,公式解比数值解大10~20 kN。因此可见式(20)的拟合精度较好,有适当富余,满足工程安全要求。 (2)在前10 000 h(约1.1年)以内,高强螺栓预紧力损失速率较快。当主缆初始应力σ0=400 MPa 时,高强螺栓预紧力损失约38.6%;当主缆初始应力σ0=700 MPa时,高强螺栓预紧力损失约42.0%;当主缆初始应力σ0=1 000 MPa时,高强螺栓预紧力损失约43.4%。这表明在自锚式悬索桥运营初期阶段(约1年左右),不同主缆初始应力时高强螺栓损失约40%,该阶段预紧力损失在整个阶段预紧力损失中占据较大比重。 当悬索桥预紧力降低至设计值70%时,索夹的抗滑安全系数不低于3.0[4]。本研究计算的1年左右预紧力损失已达到40%,安全系数将有所下降,造成索夹滑移的工程风险。即应按时开展索夹预紧力的检测及补张,确定合理的索夹张拉控制力,使索夹预紧力基本保持在较高的水平,防止工程安全问题发生。 (1)通过对高强钢丝的10年松弛试验数据进行非线性回归分析,得出高强钢丝的蠕变方程常数A、n、m,根据蠕应变与时间和初始应力的关系,利用Matlab软件,拟合得到主缆蠕变量随时间和初始应力变化的公式。对比分析公式解与有限元解发现,最大误差仅为4%,说明其拟合精度良好。 (2)通过对高强螺栓的常温蠕变试验数据进行非线性回归分析,得出高强螺栓的(蠕变)松弛方程常数A、n、m,基于时间硬化模型的应力松弛公式得到截面松弛残余应力,并在截面上积分得到预紧力Pb,Pb随时间发展的曲线趋势与有限元数值解发展趋势一致。 (3)基于蠕变力学基本假定及时间硬化蠕变模型,推导了因主缆蠕变及高强螺栓松弛造成的索夹预紧力损失公式,并建立主缆与索夹的高强螺栓预紧力损失整体有限元模型。经验证,公式解稍大于数值解,差值为10~20 kN,拟合精度良好。可为悬索桥预紧力损失检测与加固工作提供参考。 (4)在自锚式悬索桥运营初期阶段(约1年左右),不同主缆初始应力时高强螺栓损失约40%,该阶段预紧力损失在整个阶段预紧力损失中占据较大比重。
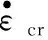

2 工程背景及有限元模型
2.1 工程背景
2.2 有限元模型建立



3 主缆索夹的预紧力损失分析
3.1 主缆的蠕变(松弛)模型计算




3.2 高强螺栓的蠕变(松弛)模型计算

4 索夹预紧力损失计算
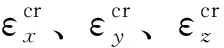

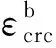



5 结论
