浅谈初中数学“读、思、说”三位一体学习法

李晓云

【摘要】本文首先提出数学成绩中下的学生面临的问题与解决问题的思路，然后对“读、思、说”三位一体学习法进行解构与逻辑系统分析，从而获得简化、易操作的“读、思、说”三位一体学习法的问题表，最后通过2个案例具体阐述该学习法在初中代数与几何教学中的应用。

【关键词】数学阅读;数学思考;说数学;学习法

一、问题的提出与解决的思路

数学成绩中下的学生普遍存在的问题：数学阅读障碍;采用被动的学习方式，缺乏自主思考;欠缺向别人问数学问题的方法，不会用数学语言与老师、同学进行表达交流。为了解决上述问题，笔者先做了三份问卷调查，分别了解初中生在数学阅读、数学思考与数学表达三方面各自的情况，分析其产生的原因，再通过文献搜索和教学实践，把“读、思、说”三位一体进行系统的研究，探索出一种新的学习方法。

二、“读、思、说”三位一体学习法的解构

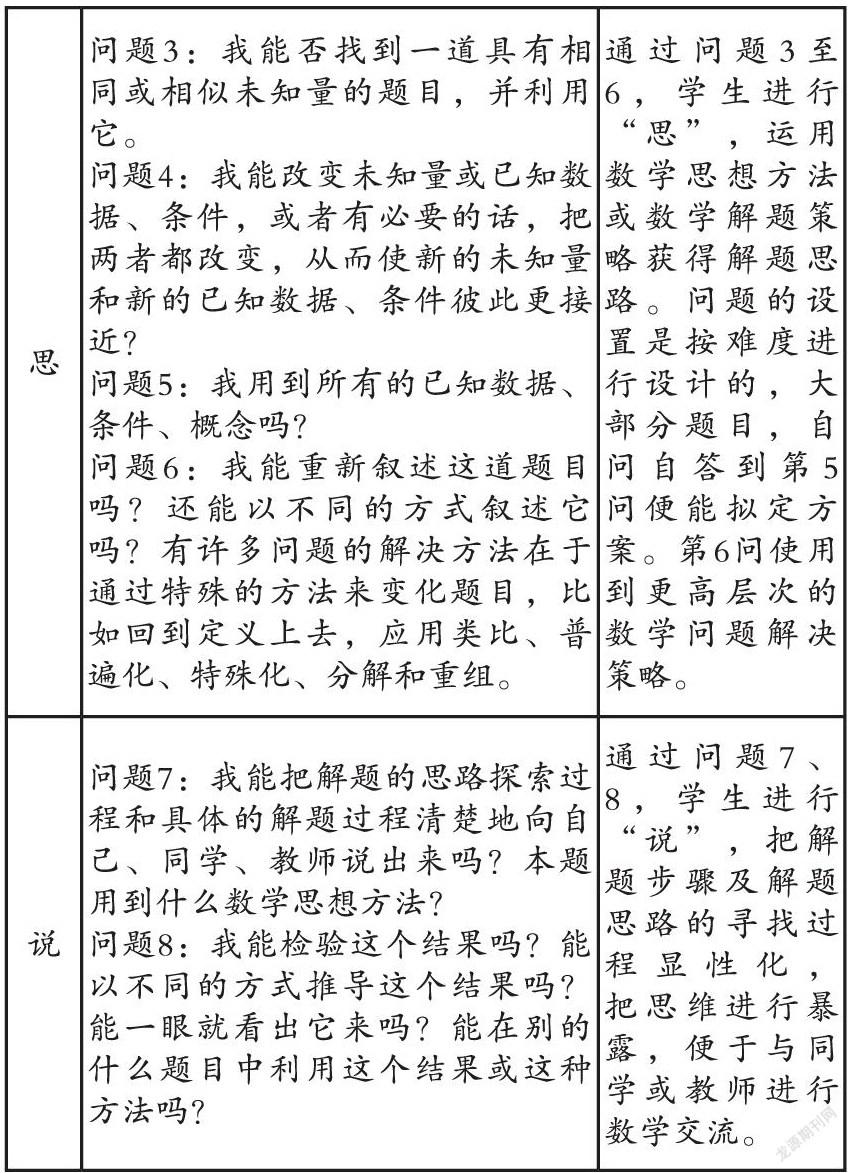
“读”即数学阅读，本文的数学阅读材料特指数学题目。“思”即数学思考，本文的“思”分为进行数学阅读的“思”与解决数学问题的“思”两个层次。“说”是指“说数学”，即数学表达，用数学语言把题目涉及的知识点，解题策略，思想方法，思路探索过程等表达给自已、同学、教师听。

“读、思、说”三者相互联系、相互制约。只有充分的“读”，才能深入开展“思”;“读”的过程中，必须带着“思”进行;“读与思”是“说”之本，没有充分的“读与思”，是“说”不出实质的东西;“读与思”需要通过“说”来外显，与外界进行信息交换，同时“说”能促进“读与思”的深化。

（一）用简化、易操作的问题表落实

自我提问的策略可以让学生更自然地习得“读、思、说”三位一体的学习法，同时提升他们的元认知水平。

三、“读、思、说”三位一体学习法的应用案例

“读、思、说”三位一体学习法采取问题串的形式开展，初期由教师引导提问，但目标是让学生内化所有问题串的提问内容与方法，最终达到自问自答，形成自身一套良好的数学学习方法。

以其在代数中的应用为例：

某工程队修建一条长1200m的道路，采用新的施工方式，工效提升了50%，结果提前4天完成任务.

（1）求这个工程队原计划每天修道路多少米？

（2）在这项工程中，如果要求工程队提前2天完成任务，那么实际平均每天修建道路的工效比原计划增加百分之几？

（下面是学生自问自答解决题目的第1个问题，自我提问的问题详见上述解答题问题表）

回答问题1：题中画线的地方就是我要注意的，画两横的是要特别注意的。

回答问题2：未知量是原计划每天修道路的米数，即原计划工效。已知数据是道路长1200m，条件是工效提升了50%和提前4天完成。已知概念是工作总量、工作效率（工效）与工作时间。我可以画成表格梳理信息点，发现原计划的工作时间也是未知量。

（数学阅读到这里已经完成的使命，接下来是进行数学思考的相应自我提问。）

回答问题3：我以前做过求相同未知量的题目，但现在工作效率与工作时间都不知道，无法直接利用它们。可以用工式得到方程组xy=1200，1.5x（y-4）=1200，但是2次的二元方程组，可能可以解，但我以前没试解过。

回答问题4：我把原计划工作效率当作已知的数据，则原计划的工作时间为          ，同理可得实际工作时间为                。当然我也可以把工作时间看成已知，那可能是另外一种做法。

回答问题5：在第4问的前提下，我还有一个条件没用上，那就是提前4天完成，即原计划工作时间=实际工作时间+4。

（由于解题思路已经找到，所以数学思考的自我提问结束，不必要提问第6个问题）

回答问题7：思路探索过程就是回答前5问的过程，具体的解题过程如下（略）。本题用到了方程思想与代入消元的方法。

回答问题8：分式方程需要检验分母不为0，而且数据合理。这道题还有其它解法，前面的回答过程可以知道。现在我能一眼看出本题的解题思路。本题目第2个问需要用到第1问的结论。

四、结束语

由于本文的理论研究欠缺，所以对“读、思、说”三位一体学习方法缺乏一个更系统更清晰的论述。问题表里的问题还不够精炼、通俗化，如果能用学生熟悉的語言进行简化表述，学生使用会更流畅。“读、思、说”三位一体学习方法的应用案例，对“如何读、如何思、如何说”阐述得不够清晰。不管如何，本文的研究已经开启了一扇能让学生自主学习，把思维暴露、显性化，用数学语言进行表达与交流的门。

【参考文献】

[1] 历小康.数学阅读能力的培养研究[J].数学教育学报，2004，5.

[2] 何小亚.数学学与教的心理学（第二版）[M].广州：华南理工大学出版社，2016.

[3] 斯莱文.教育心理学（第七版）[M].北京：人民邮政出版社，2010.

[4] 波利亚.怎样解题[M].阎育苏，译.北京：科学出版社，1984.

（责任编辑：洪冬梅）