声表面波在空心圆柱体中的传播特性分析

吴荣兴, 邱森, 张青艳, 郑东

（宁波职业技术学院应用力学研究所，浙江宁波，315800）

0 引言

声表面波因其具有激发和接收简单、传播能量衰减较小、检测领域广泛等优点，在板型和圆柱类结构中获得了广泛的应用[1]。高祥熙等利用超声表面波对飞机液压导管的裂纹进行了检测[2]。徐志祥等采用有限元仿真分析表面波在涂层平板表面的传播规律，利用Morse小波分解多频表面波信号，提取最大幅值单一频率的缺陷时域信号从而确定表面缺陷位置[3]。宋大成等研究了声表面波与一定深度范围内的V型裂纹的作用过程，采用有限元方法模拟了热弹机制下，线性脉冲激光源激发的声表面波信号在金属材料中的传输过程，以及声表面波与V型裂纹的相互作用[4]。吴荣兴等分析了声表面波在混凝土材料特性检测和飞机结冰厚度检测等应用[5-7]。

金属圆柱作为常见的结构类型，其表面缺陷检测和管道类传感检测一直是检测领域重要的方向。声表面波在圆柱表面传播会产生色散和相移现象，这与声表面波在平板上的传播规律不同，一定程度影响了检测表面缺陷的位置精度[8]。徐志祥等提出通过扫描检测点的方法确定缺陷的位置，给出了表面波在表面缺陷附近的传播路径和缺陷深度计算公式[9]。在这些分析过程中，除了极少数情况下，一般无法获得其精确解析解，主要原因是声表面波在空心圆柱体传播时其边界条件和求解过程将更加复杂。本文分析了声表面波在空心圆柱体内传播的特性，为声表面波在空心圆柱体的检测奠定了理论基础和方法。

1 基本方程

声表面波在如图1所示的空心圆柱体内沿着圆周方向传播，其内径、外径和圆周转角分别为r1、r2和θ，z轴垂直于的圆柱体横截面，文中不考虑声表面波沿着z轴方向传播。当声表表面波沿着平板传播时候，我们主要考虑二维截面，沿着x1方向传播，但是在x2方向发生衰减。这里沿着圆周方向传播，沿着半径方向发生衰减。

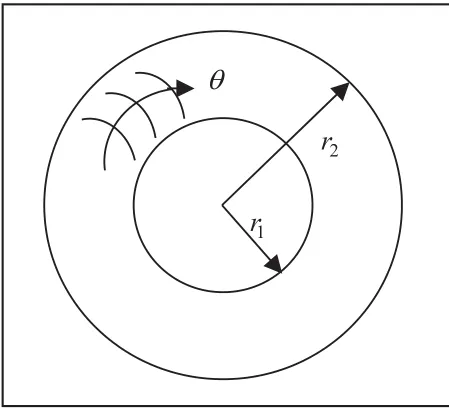
图1 空心圆柱体截面图

各个方向的位移可以写为

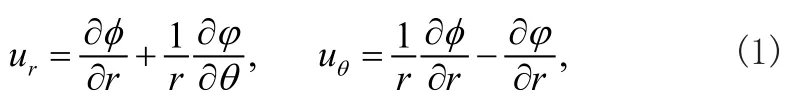
式中ur和uθ分别是半径r和转角θ的函数，而势函数φ和ϕ必须满足圆柱坐标下的波动方程为

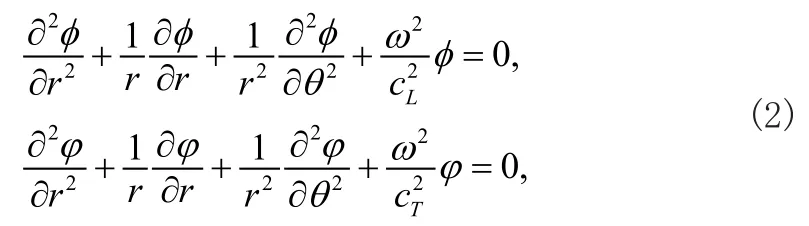
式中

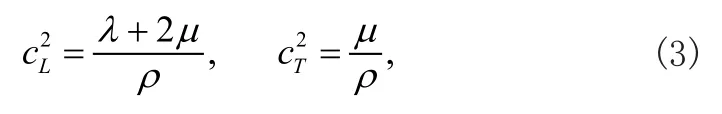
分别定义为弹性介质的纵波和横波波速，其中,λµ和ρ分别为弹性固体的拉梅常数和密度。根据弹性材料的本构关系，应力可以表示为

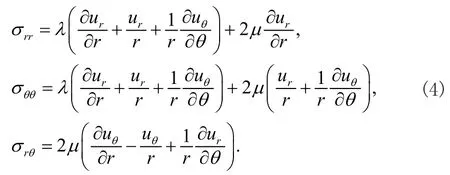
对于如图1所示圆柱体的内外表面，其边界条件为

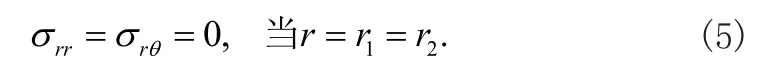
可以进一步假设势函数为

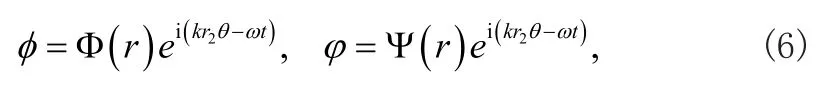
式中k和t分别式角波数和时间变量。将式(6)代入式(2)，省略掉e−iω t可以得到

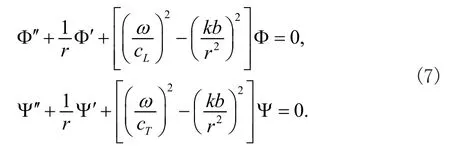
式中的通解为

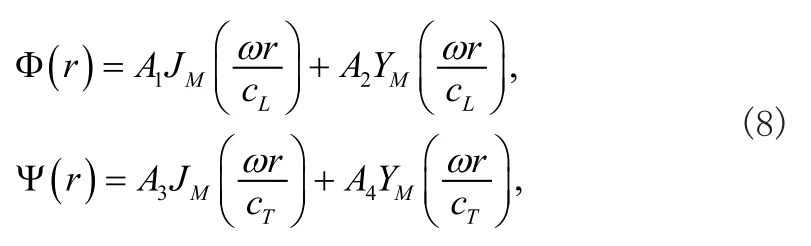
式中JM和YM分别是第一类和第二类贝塞尔函数，A1(A2,A3,A4)为振幅表示式，其他参数定义如下

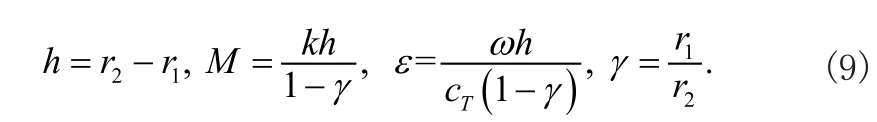
将式(8)代入应力表达式(4)，可以得到

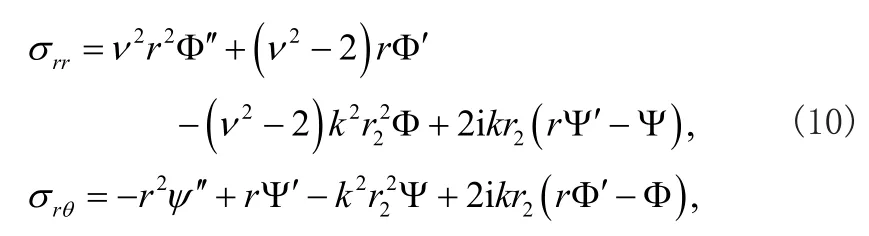
可以将应力表达式(10)代入边界条件式(5)，可以得到振幅A1(A2,A3,A4)的线性齐次方程组。若这些振幅存在非零解，那么必须要求系数行列式的值必须为零，这样就得了声表面波在圆柱表面传播的频散方程如下

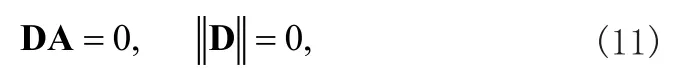
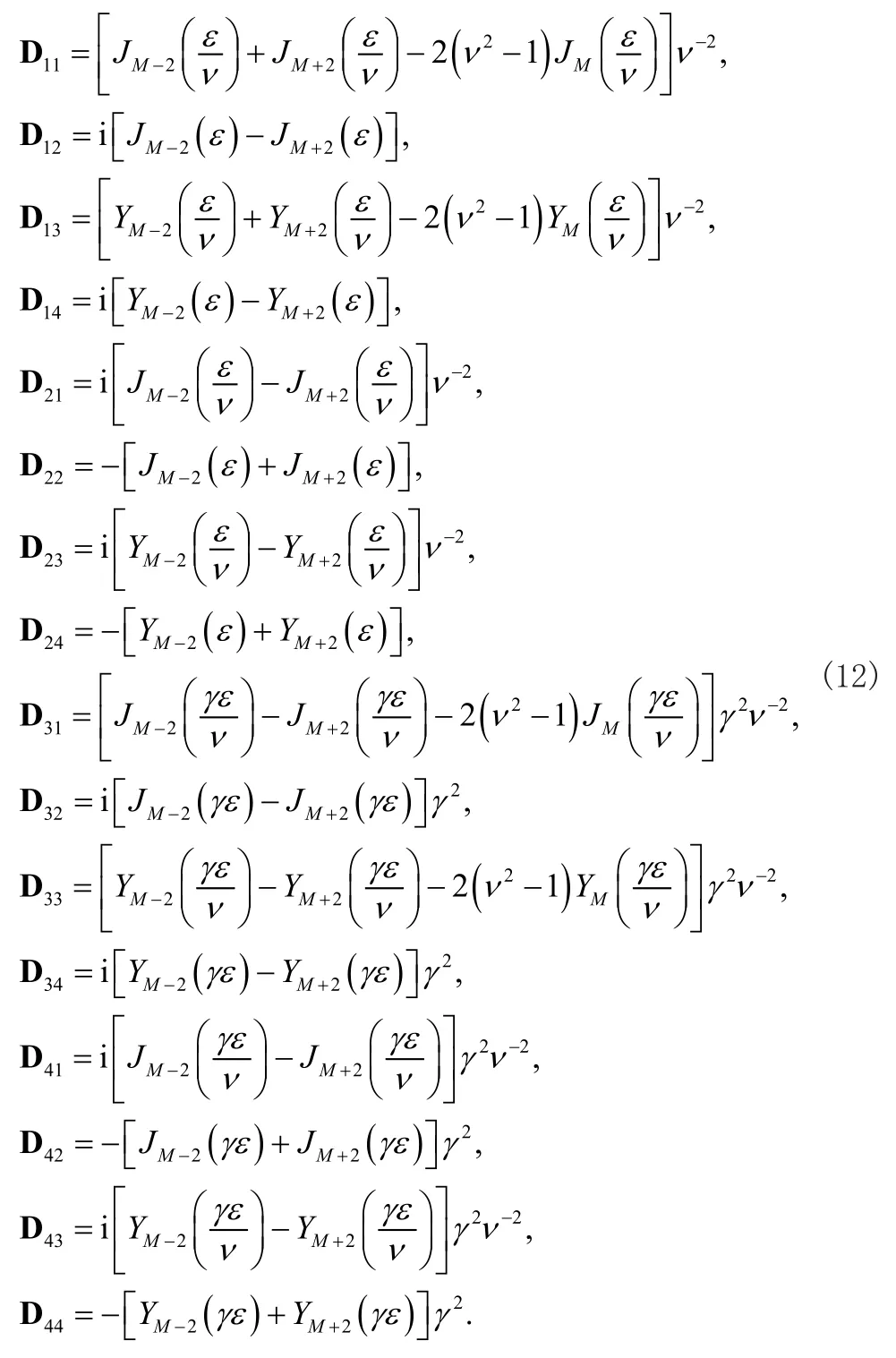
这样就完整建立了声表面波在空心圆柱体传播的频散方程。为了进一步分析其振动特性，根据式(11)的计算结果，我们可以得到多个声表面波的解，根据线性叠加原理，可以重写位移为

式中

通过位移表达式可以确定声表面波的振动模态形式，主要为对称振动和反对称振动模态。这里的位移表达式和平板的位移表达式存在着明显不同，平板的位移表达式是不考虑曲率的影响，因此引用的势函数也是不同的，其表达式为

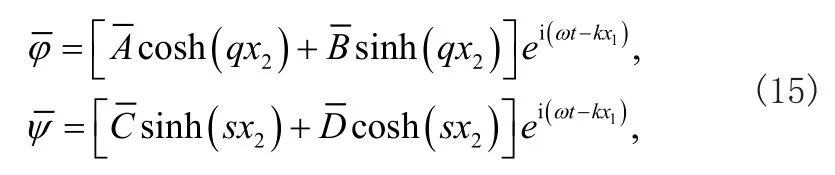
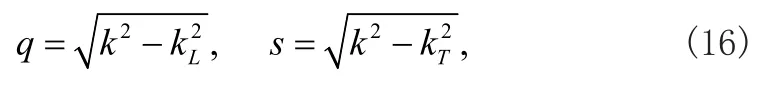
式中kL和kT分别为单层板中纵波和横波的波数

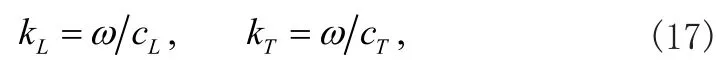
式中cL和cT分别为单层板的纵波和横波波速，如式(3)所示。通过式(15)-(18)和前面的推导表达式比较可以明显看出位移表达的不同，同时由于曲率的存在，声表面波的频率和位移都将发生改变，而这些改变对于声表面波的检测来说非常重要。

2 计算结果

可以对式(11)进行求解，这里设定的材料参数为空心圆柱铝管，相关参数定义如下

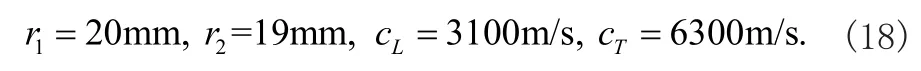
可以进一步定义周向导波的相速度为[10]

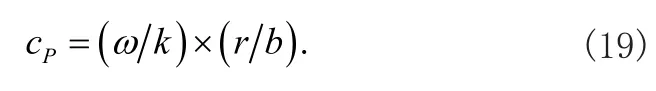
这样绘制了不同内径空心铝圆柱体的声表面波的频散关系如图2-3所示。

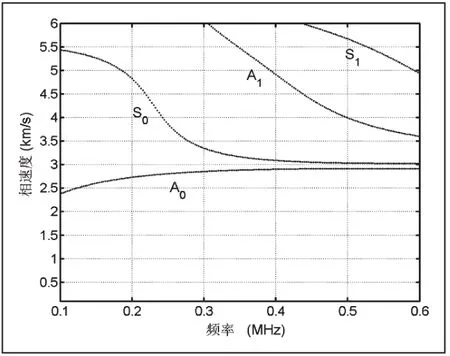
图2 空心铝圆柱的声表面波频散关系(r2=19mm)

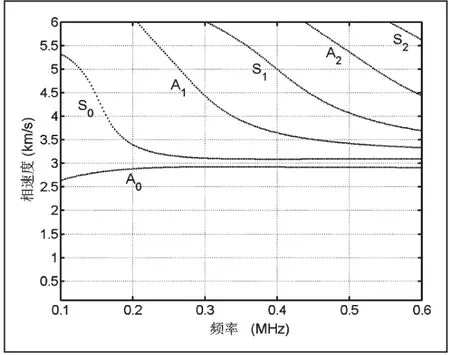
图3 空心铝圆柱的声表面波频散关系(r2=18.5mm)

从图2-4中可以观察到随着频率的增加，空心铝圆柱中的声表面波将会出现一系列对称和反对称模态，这为空心圆柱体的各类检测提供了多模态选择[10]。先前的研究表明低阶的振动模态通常被用来作为检测的工作模态，例如零阶对称和反对称模态，主要原因是低阶模态比较容易激发和接收信号，高阶模态激发和接收需要更加精确[7]。同样发现随着空心铝圆柱体壁厚的不断增加，在同一频率尺度内各种振动模态将出现更多，这和平面板的结果不一致[11-12]。但是与平板中传播的声表面波一样，随着频率的不断增加，空心铝圆柱体内的声表面波的各模态的波速都将趋于瑞利波波速[13]。

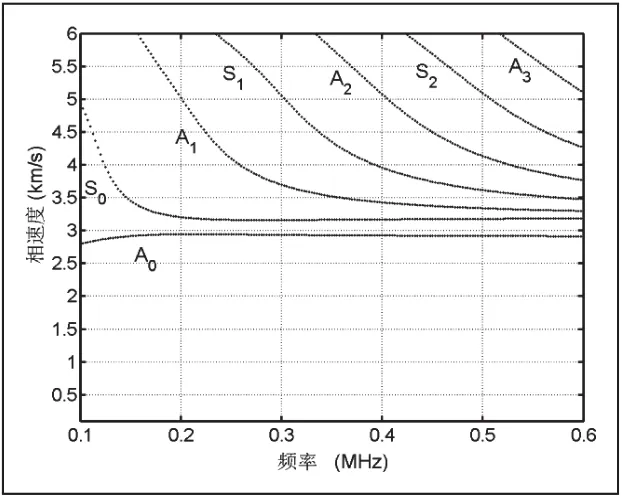
图4 空心铝圆柱的声表面波频散关系(r2=18mm)

同样根据式（13），我们可以绘制出声表面波在圆柱体传播的位移图如图5-图8所示。

这里需要注意的是图5-8的纵坐标是各阶模态的归一化位移，因为在计算过程中是利用振幅比来求解声表面波的位移，因此就不存在单位。从图5-8可以发现，圆柱体内的声表面波的位移仍然呈现对称和反对称模态[14]。但是由于存在一定的曲率，对称和反对称模态略显变异，通过绘制不同曲率的位移图表明曲率对于位移的影响较为明显。这样在实际工程检测中，必须注意模态的选择，过去的研究表明高阶模态由于信号发射和接受比较困难，通常选择低频模态。现在的研究表明相比于平板，圆柱空心体的声表面波的低阶模态受曲率影响较为明显，实际检测时候必须考虑这些影响。

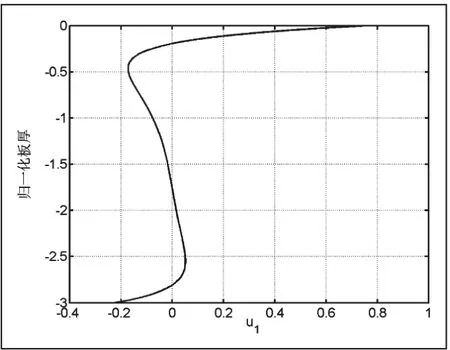
图5 空心铝圆柱中u1 的位移(r2=18mm)

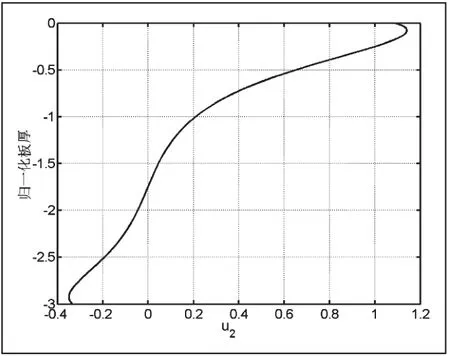
图6 空心铝圆柱中u2 的位移(r2=18mm)

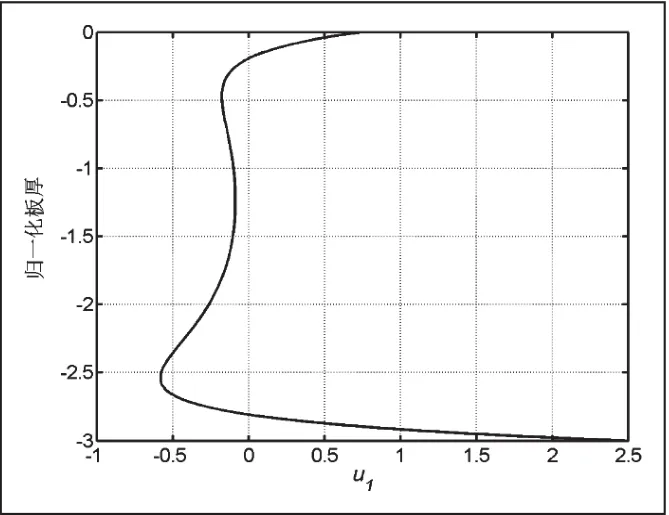
图7 空心铝圆柱中u1 的位移(r2=18mm)

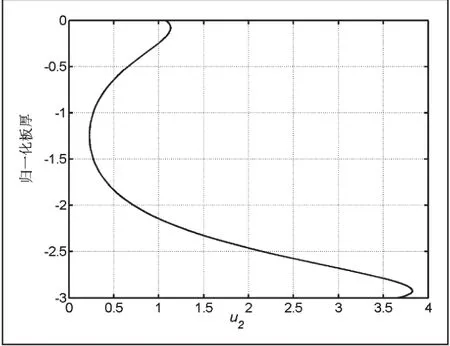
图8 空心铝圆柱中u2 的位移(r2=18mm)

3 结论

分析了声表面波在空心铝圆柱体内的传播特性，建立了声表面波的频散方程。通过数值求解绘制了不同壁厚的空心铝圆柱体的声表面波频散关系。计算结果表明声表面波在空心圆柱体沿着圆周方向传播时将会出现多个对称和反对称模态，同时随着频率的增加，各种模态的相速度都将趋于瑞利波的波速。这里建立的模型和计算结果为实际的声表面波圆柱体检测奠定了基础。