知原理 重探究

王书贤 郭建理

【摘 要】尺规作图是帮助学生从感性到理性，从直观操作到逻辑推理，并建立几何直观的有效工具。研究者对尺规作图的命题现状提出问题，以江苏省近三年尺规作图的中考试题为研究对象，结合题量变化、试题分析，具体阐述了尺规作图题对学生空间观念、几何直观以及推理能力的培养。

【关键词】尺规作图;命题分析;中考试题

【作者简介】王书贤，常熟理工学院在读学生;郭建理，高级教师，江苏省特级教师，曾荣获全国优秀教师，第八届中学数学教育奖——“苏步青数学教育奖”二等奖等。

尺规作图是帮助学生从感性到理性，从直观操作到逻辑推理，并建立几何直观的有效工具。在信息高度发展的今天，尺规作图仍有丰富的教育价值。尺规作图是一种学生实际动手操作的过程，与图形运动有着密切的联系，具有不可替代的直观性;其也是问题解决中不可分割的一部分[1]。此外，由于尺规作图只利用无刻度直尺和圓规这两种工具作图，对于学生而言具有一定的挑战性，例如在尺规作图的过程中，所规定的是无刻度直尺，这使得直尺只能用来作直线，而不能进行测量，这一限制将会激发学生思考，进而培养学生的思维能力与创新能力。同时，尺规作图对学生推理能力的培养有较大的促进作用，使学生加深对几何知识的理解。因此，在几何教学强调对思维能力与推理能力培养的今天，尺规作图理应得到足够的重视。本文从中考命题入手，通过对尺规作图题的考查情况进行分析，以期对教师的教学有所启发。

一、尺规作图的命题现状

（一）尺规作图的题量变化

为研究江苏省对尺规作图问题的考查，笔者查阅了江苏省13个地市近3年的数学中考题，并将涉及尺规作图的地市和题号进行统计（见表1）。

从考查地区来看，2018年只有南京、无锡、南通、淮安、常州5个地市考查了尺规作图题，到了2020年共有11个地市考查尺规作图题，可见越来越多的地区在中考中加大了对于尺规作图题的考查;从考题分布来看，主要在解答题进行考查，选择题和填空题也有涉及;从题量来看，尺规作图题的考查次数明显增多，可见近几年江苏省数学中考对尺规作图的考查是有所加强的，并且重视程度不断提高。

（二）尺规作图的命题方式

1.补全式

补全式，即题目给出作法的全部或者部分过程，要求学生理解作法，补全作图依据或作图过程[2]。这样的考题不仅要求学生依据题目作出目标图形，而且需要学生深刻理解每一步操作背后的原理，做到知行合一。

例1（2018年南通16）下面是“作一个30°角”的尺规作图过程。

已知：平面内一点A。

求作：∠A，使得∠A=30°。

作图：如图1，（1）作射线AB;（2）在射线AB上取一点O，以O为圆心，OA为半径作圆，与射线AB相交于点C;（3）以C为圆心，OC为半径作弧，与⊙O交于点D，作射线AD，∠DAB即为所求的角。

请回答：该尺规作图的依据       。

本题考查运用尺规作出特殊角，以及运用等边三角形的判定和性质，圆周角定理等知识解决问题的能力。解答此类题目，首先应知道确定图形所需要的元素;其次明确达成作图对象需要应用的知识点;接着厘清每一步作法与确定图形元素之间的关系;最后明白整个作法的数学原理[3]。

这类试题关注作图依据，不仅需要学生读懂尺规作图的作法，而且需要学生逆向证明所作的图形符合要求，具有一定的思维能力。这很好地体现了知行合一，以及尺规作图“知原理、重探究”的教学价值取向，充分发展了学生的空间观念、几何直观、逻辑推理等数学核心素养。在教学中，教师应引导学生深刻理解每一步作法背后的依据，体现步步有据，使学生对作法的“理”认识到位。

简解：先根据作图得出OD=OC=CD，即△OCD为等边三角形，据此可得 ∠COD=60°，再根据圆周角定理知∠DAC=12∠COD=30°，从而得出答案：三边相等的三角形是等边三角形;圆周角的度数等于圆心角度数的一半。

2.实操式

实操式，即根据题目要求，用尺规作出相应图形，只保留作图痕迹，不要求写作法。试题常以五种基本作图法作为本源，对需要确定的对象属性进行深层次、多角度的联想。

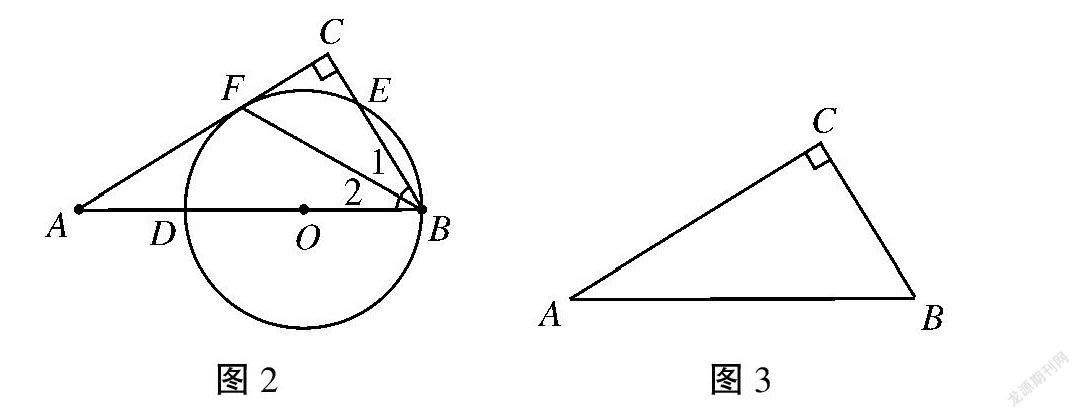
例2（2019 年宿迁24）在Rt△ABC中，∠C=90°。

（1）如图2，点O在斜边AB上，以点O为圆心，OB长为半径的圆交AB于点D，交BC于点E，与边AC相切于点F，求证：∠1=∠2。

（2）在图3中作⊙M，使它满足以下条件：

①圆心在边AB上;②经过点B;③与边AC相切。（尺规作图，只保留作图痕迹，不要求写作法）

本题将尺规作图与圆和切线的性质相结合，主要考查角平分线和线段垂直平分线的作法。掌握连接圆心和切点的半径与切线垂直是解题的关键，其突出了对学生推理能力的考查。这样的命题方式常见于解答题中，以基本作图作为出发点，将推理蕴含其中。

此类问题需要学生熟练掌握《义务教育数学课程标准（2011年版）》（以下简称课程标准）中所要求的五种基本作图法，将书本知识与实际动手操作结合起来，不但可以提高学生的空间观念、几何观念、逻辑推理等数学核心素养，还可以让学生体会到尺规作图的简单精确与数学之美[4]。在教学中，教师应以教材为本，深化整体教学，使学生明确教材中的基本作图方法，掌握各个知识点之间的内在联系。对于解决此类尺规作图的问题，教师可以参照波利亚的解题四步骤来组织教学。

简解：（1）连接OF，可证得OF//BC，结合平行线和圆的性质可求得∠1=∠OFB=∠2。

（2）由（1）可知切点是∠ABC的角平分线和AC的交点，圆心在BF的垂直平分线上，由此可作出⊙M。

3.应用式

应用式，即题目给出作图语言、作图痕迹，以此为条件进行应用。这类考题考查角度新颖，将题目的已知条件通过尺规作图的作法表达出来，要求学生理解作法，并能够根据作法找出隐藏的已知条件进行其他计算或证明。较补全式、实操式两种类型而言，应用式考查要求相对较低，只要求学生读懂做法即可。

例3（2020年苏州18）如图4，已知∠MON是一个锐角，以点O为圆心，任意长为半径画弧，分别交OM、ON于点A、B，再分别以点A、B为圆心，大于12AB长为半径画弧，两弧交于点C，画射线OC。过点A作AD∥ON，交射线OC于点D，过点D作DE⊥OC，交ON于点E。设OA=10，DE=12，则sin∠MON=    。

本题借用作图语言、作图痕迹，间接地给出“OD平分∠MON”这个已知条件，考查学生对角平分线基本尺规作图的了解。本题并未要求学生按步骤作出图形，而是以阅读题目条件的形式让学生对作图语言进行推理，再通過计算求得角的正弦值。

这类问题需要学生阅读并理解作图步骤，判断作出的几何图形，再分析推理得出作图所表示的信息，最后进行解题。在教学中，教师可引导学生尝试操作，理解图形产生的过程，通过问题串的形式，及时梳理学生在探究过程中发现的问题，并鼓励学生用数学语言来表达自己的数学思考，带领学生经历解决问题的全过程，不断提高学生发现和提出问题以及分析和解决问题的能力。

简解：连接DB，过点D作DH⊥ON于H。首先，证明四边形AOBD是菱形;其次，通过解直角三角形可求出DH，即可解决问题。故答案为2425。

二、尺规作图的命题预测

（一）纵向分析

中考考题具有良好的导向作用。从近几年江苏省中考数学试题来看，尺规作图题的考查类型以补全式、实操式和应用式为主。对于从未考查过尺规作图的徐州市和连云港市，今后数学中考题可能会优先命制实操式类型的试题，即给出部分几何图形，学生根据作图要求，作出相应的图形，主要考查基本作图的操作，具体可参照上文例2。

对于已考查过尺规作图试题的地区，如苏州市，不会马上提高试题难度，可能会涉及圆、三角形、平行四边形等性质定理，并在已考查过的试题的基础上进行创新。而无锡市此前的试题综合性强，灵活度高，难度大，对于学生的逻辑推理、分析问题、空间想象能力都有较高的要求，今后将会继续在此基础上考查尺规作图，并提高试题的创新性。

（二）横向分析

目前，江苏省高考与全国高考已经接轨，中考题也会向全国其他省市看齐，这是未来的大趋势。因此，借鉴全国数学中考题中有关尺规作图的考查，江苏省尺规作图三大类型题目可从作图背景或作图工具进行试题创新和改编。虽然江苏省有关此类的尺规作图题已有涉及，但相较于全国其他走在尺规作图命题前沿的省市，还不够成熟。

从全国中考数学的真题来看，天津市的网格作图题比较热门，属于天津中考数学的常考题型，或许会对未来江苏各地市的命题有借鉴意义。此外，限制作图工具仅为无刻度直尺或圆规的题型也应值得关注，比如江西省中考数学近几年考查了无刻度的直尺作图题;2007年南京市中考数学考查了圆规作图题，这或许成为未来命题的新形式。

三、教学建议

根据课程标准对尺规作图的教学要求，近几年江苏省中考数学试题从题材选择到问题设计均进行了适当创新，研究这些试题的命题意图，分析课程标准的导向作用，有助于教师把握尺规作图的教学要求与考查方向。尺规作图是初中几何中训练学生工具操作、几何语言叙述和逻辑推理能力的重要内容，在课堂教学中，教师应注意以下几个方面。

1.转变思想观念，促进学生能力培养

尺规作图作为最基本的作图方法，具有创新性与逻辑性，尺规作图是平面几何的核心内容，贯穿于整个数学学习之中。在教学中，教师要转变只关注知识技能的思想观念，应把尺规作图作为培养学生逻辑思维与创新精神的重要课程资源，通过教学助推学生对数学知识原理的理解，让学生进一步实践并感悟数形结合与转化的数学思想方法，开发学生思维，促进学生能力培养。

2.丰富数学实验，提高学生动手能力

2021年7月12日，第14届国际数学教育大会（ICME-14）在华东师范大学开幕，在“中国数学教育特色主题活动”中，江苏省教育科学研究院的“数学实验——中国中小学数学学习的变革”，作为其中一个主题在会上展示。数学实验，在一定程度上影响着中学数学教与学的变革。教学中，教师要帮助学生理解算理、掌握算法、发展运算能力，培养学生数形结合以及逻辑推理能力。尺规作图是初中几何教学的重点，是最基础的数学实验之一，教学中一题多变给学生提供灵活的实验平台，一题多解、一图多做，多角度、全方位地开启学生的发散性思维，教师要大胆放手让学生动手操作，观察思考，探究和内化原理。

3.规范数学语言，锤炼学生表达能力

课程标准要求学生会用数学的眼光观察世界，会用数学的思维思考世界，会用数学的语言表达世界。用数学语言表达问题时要求规范、准确、简洁、清晰，而学生在尺规作图的学习中，往往只会作图，欠缺表达。在教学中，教师应首先训练学生掌握尺规作图的语言表达——已知、求作、作法，做到层次分明;其次熟练掌握常用作图语言，使作法表达规范、准确;最后，用基本尺规作图的作法表达时，无须重复作图的详细过程，用一句话概括即可，做到言简意赅。教学中规范学生的数学语言，锤炼学生的表达能力，为学生后续的解析几何、立体几何的作图表达奠定基础。

近几年，江苏省逐渐重视尺规作图试题，各地市的尺规作图题量明显增加，试题考查类型灵活多样，对学生的直观思维、推理能力、空间观念等数学核心素养有所提高，激发了学生的学习兴趣和创造性，促进了学生的理性思维能力和动手操作能力的发展，为学生进行更高层次的数学学习奠定基础。

参考文献：

[1]乐嗣康，崔雪芳，张奠宙.尺规作图教学的现代意义[J].中学数学月刊，2005（12）：7-9.

[2]诸士金.第11讲：尺规作图[J].中学数学教学参考，2020（1/2）：112-116.

[3]肖世兵.中考“尺规作图”命题分析及预测[J].中小学数学（初中版），2020（7）：88-89.

[4]赵轩，王尚志.从一道中考题说起：尺规作图中的数学思想方法初探[J].数学通报，2016（3）：30-33.

（责任编辑：陆顺演）