基于电磁阻尼的振动能量回收装置研究

卢 涛，魏 勇，余厚全，宋钢兵

（1.长江大学电子信息学院，湖北荆州 434023；2.休斯顿大学机械工程学院，美国休斯顿77504）

引言

随着电子技术的发展，基于无线传感器网络的结构健康监测系统得到了广泛的应用，相关的设备一般具有远离电网、传感器节点数量多、功耗低、无线通信和无人值守的特点［1］。通常结构健康监测系统中的无线传感器节点使用电化学电池供电，然而电化学电池存在着使用寿命短、需要频繁更换和化学物污染环境等缺点，这些节点供电问题正日益凸显。因此，寻找一种新的清洁能源，为结构健康监测系统提供一种新的电源解决方案具有重要的工程意义。自然界中存在不同频率和强度的振动能，如高楼和桥梁存在着随风持续稳定的摆动现象［2］，采集这些振动能并转化成电能［3－5］，不仅能够有效地利用建筑物的振动能，还解决了建筑物结构健康监测系统的供电问题［6－9］。

振动能量收集方式主要有三种：压电式、静电式和电磁式。压电式的压电陶瓷抗疲劳度弱，容易损坏，加之产生的电能时间短和幅度高，不容易进行转换和收集，导致在能量回收应用中受限；而静电式的振动能采集器需要外加电源才能工作，一些场合如：野外、锅炉和辐射区等不方便安装电源，因此也限制了这种方法的使用；电磁式振动能量采集器适用于多种频率和振动幅度的场合，尺寸不受限制，最终成为众多学者研究的热点。DAYAL 等［10］研究垂直方向的振动能量回收，利用磁铁在螺旋线圈周围运动产生电磁感应，将振动能转化为电压达几百毫伏的电能；基于经典电磁振动模型，国内学者张端等［11］提出了高效电磁式振动能量回收模型，动态仿真表明模型中单个线圈电压为1.2 V，空载时最大有效功率为474.1 mW，带负载功率达到118.5 mW；王佩红［12］研究设计了一种三明治结构的微型电磁式振动能量回收装置，所收集的电能功率为21.2 uW，输出电压峰峰值达到163 mV。上述实验实现了垂直方向上微瓦甚至毫瓦级别的振动能量回收，充分说明电磁式装置收集能量的可行性。在水平振动能量回收方面，华中科技大学的沈文爱等［13］设计了大幅度摆锤式电磁能量回收装置，可以收集来自交通、自然风和地震中的振动能，装置最大有效输出功率174.5 mW 能量。但由于变速箱的结构较为复杂，未见推广使用。基于上述研究，本文提出一种新型电磁阻尼振动能量回收装置的方案。

1 物理模型与理论分析

1.1 电磁阻尼器的理论模型

图1为基于摩擦力的调谐质量块阻尼器模型［14］，其主要由质量块、弹簧和结构体组成。当模型受到高层建筑物的水平振动激励作用时，由于两根弹簧的弹性系数k相同，质量块m将做左右往复运动，质量块的下表面与结构体之间将产生大小为μmg 的滑动摩擦力（μ为摩擦系数）。由于质量块的滑动摩擦作用，振动能将转化为热能消耗掉。

图1中质量块的运动公式为：

图1 调谐质量块阻尼器模型Fig.1 Tuned mass damper model

式中：x、˙和分别表示质量块的运动位移、速度和加速度。表示符号函数，当质量块右移和左移时，值为±1，标志着质量块受到滑动摩擦力的方向。

假如对上述装置进行改进，用电磁阻尼力取代摩擦力，那么通过电磁感应效应，振动能也可以转换成电能［12，15－17］。这为我们设计水平方向上振动能量回收装置提供了解决方案。

如图2 为基于电磁阻尼的能量回收模型。模型中的质量块为环形磁钢，磁钢的外侧为环形螺线圈。结构体振动时将导致磁钢发生强迫振动，进而在螺线圈上产生交变的电压信号。假设静止状态下磁钢的中心为坐标原点，运动状态下的磁钢相对于原点的位移为x，结构体相对于原点的位移为y，磁钢受到的螺线圈电磁阻尼和支架机械阻尼之和cT，根据牛顿第二定律，可得磁钢的运动方程：

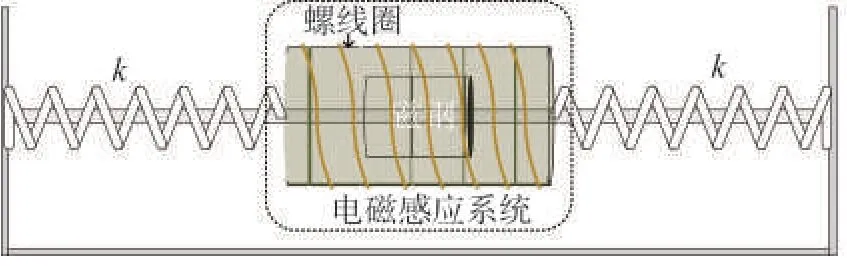
图2 基于电磁阻尼的能量回收模型Fig.2 Energy recovery model based on electromagnetic damping

1.2 电磁阻尼器模型的特性分析

能量回收效率是评价一个能量回收装置性能的关键因素，以下分析如图2 所示模型的回收功率。设结构体的运动为简谐函数：

式中：A为幅值；ω为角频率。与结构体相比较，磁钢的位移是一种频率与之一致，但幅值和相位均不同的简谐函数：

将式（3）和式（4）代入式（2），即可计算出简谐函数激励下的磁钢幅值与结构体幅值比B/A以及磁钢的相角［12］：

式中：ωn=为拾振系统的固有频率；ξT=，ξT表示电磁阻尼器的总阻尼比。

图3 为式（5）的数值模拟结果，曲线表明：①当ξT＜0.1 时，磁钢振幅的峰值出现在=1 附近，且总阻尼比ξT越小，振幅幅值越大；②当0.1＜ξT＜1时，振幅的峰值随着ξT的增大向＜1的方向偏移。因此，为了让磁钢获得更大的振幅从而回收更多的电能，在设计实际能量回收装置时需要注意：①调整弹簧的弹性系数k或者改变磁钢的重量m，当二者满足ωn==ω时，磁钢的振幅最大；②尽可能地减小总阻尼比ξT，当电磁阻尼一定的情况下，减小磁钢的支架的机械阻尼成为最佳解决方案。

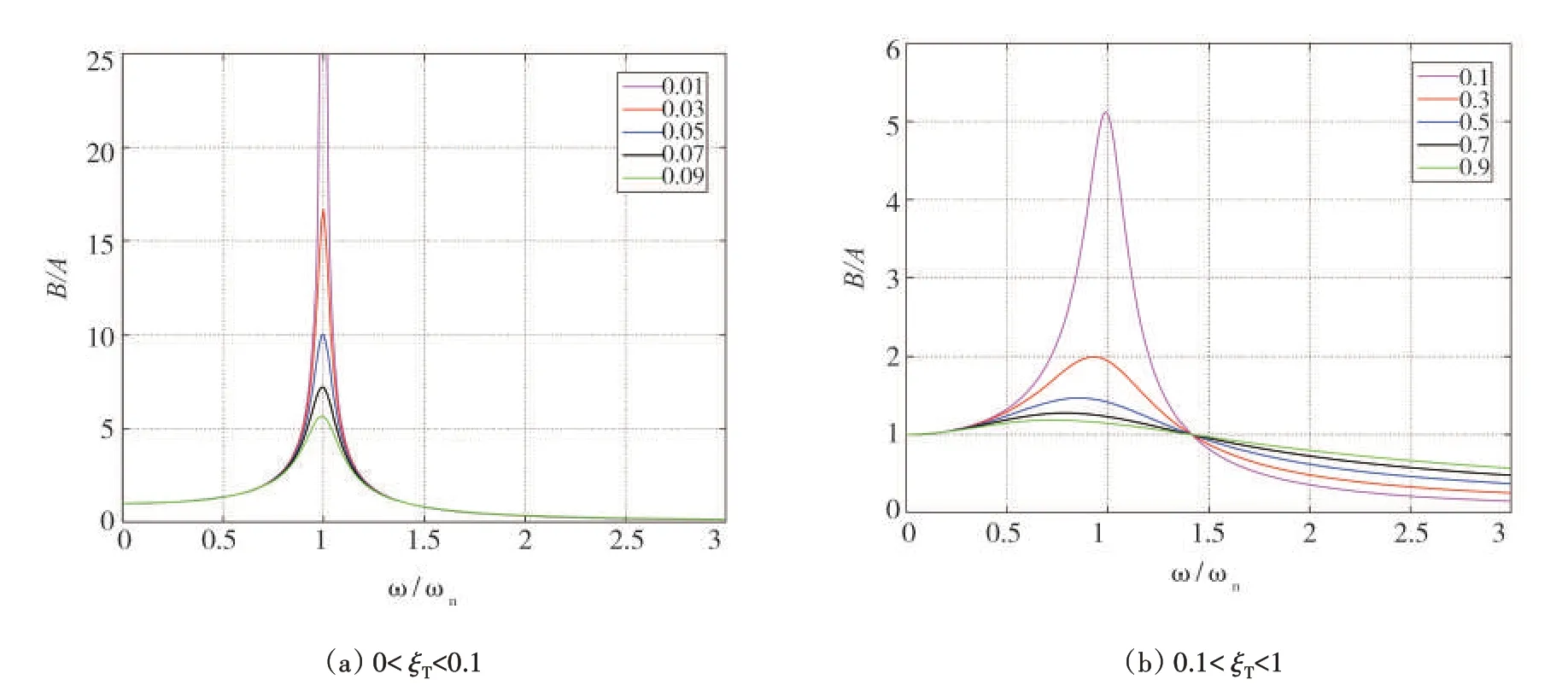
图3 幅频响应曲线Fig.3 Amplitude frequency response curve

图4 0＜ξT＜1时的相频响应曲线Fig.4 Phase frequency response curve when 0＜ξT＜1

假设系统的机械阻尼足够小，振动能几乎全部转化为电能，则电磁阻尼器收集的能量的平均功率可以表示为：

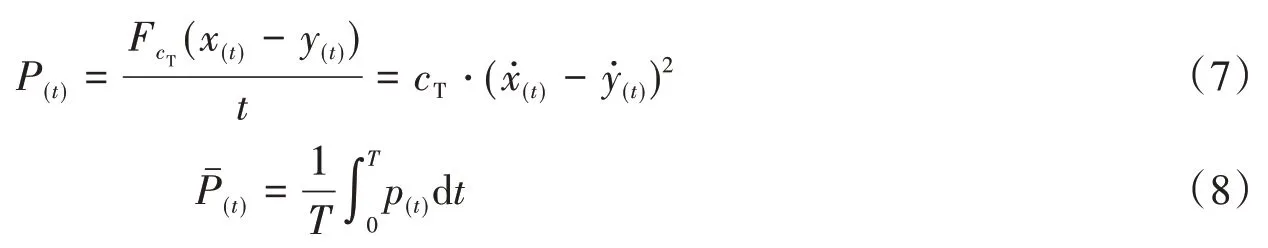
将式（5）和式（6）以及y(t)=Acos(ωt)代入式（8）得［18］：

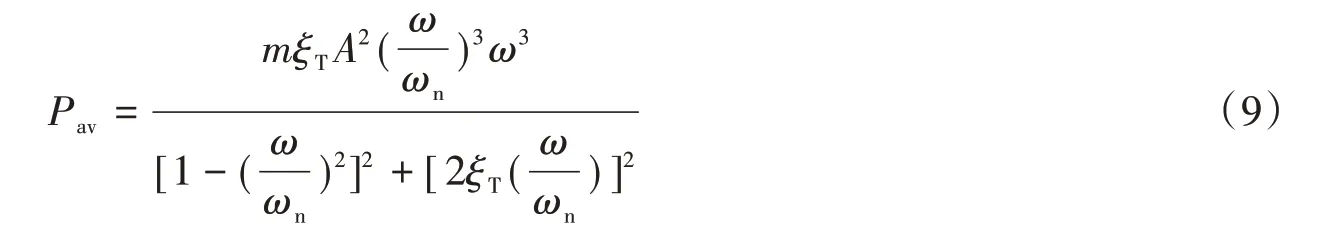
式（9）的数值模拟结果如图5 所示，曲线表明：①当频率比=1 时，平均功率Pav达到最大值；②当频率比=1时，平均功率Pav随着阻尼比ξT的增大而减小，这与图3的结论一致。上述分析为设计实际能量回收装置提供了理论指导。

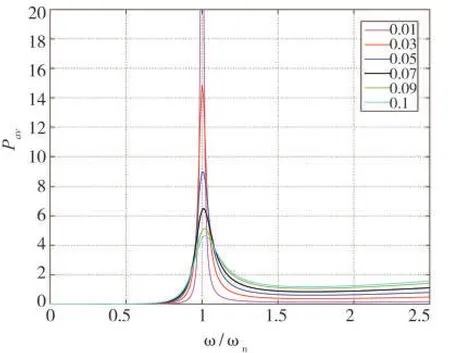
图5 0＜ξT＜0.1时的功率频率比响应曲线Fig.5 Power-frequency ratio response curve when 0＜ξT＜0.1

2 电磁阻尼器和电磁振动体的设计方案

2.1 电磁阻尼器的设计方案

根据上述模型分析，提出了如图6所示的电磁阻尼器设计方案［14］。包括1弹簧、2螺旋线圈、3环形磁钢、4隔磁板、5无磁轴承、6无磁滑杆、7支架和8角钢。为了提高系统的转化效率，拟采取的技术手段有：①采用多个环形磁钢和螺旋线圈串联而成的电磁感应系统，提高输出电压的幅值；②采用隔磁板分隔磁钢之间的磁场串扰，提高系统的磁通量，进而提高转化效率。

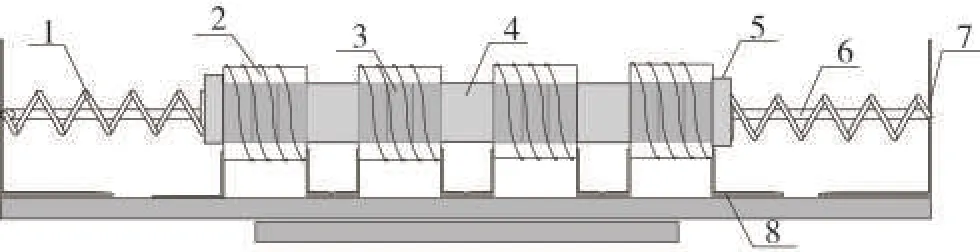
图6 电磁阻尼器设计方案Fig.6 Design scheme of electromagnetic damper

2.2 电磁振动体的设计方案

为了模拟自然界中建筑物的振动，并带动电磁阻尼器工作，提出了如图7 所示的电磁振动体设计方案［14－16］。由简易振动台和电磁阻尼器两部分组成。振动台由基座、弹性钢片和带偏心锤电机组成，能够较好地模拟自然界中的水平振动，特别是类似高层建筑物的振动环境。

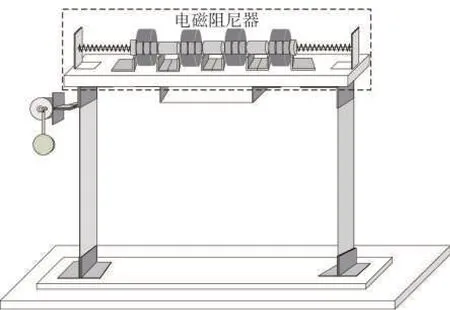
图7 电磁振动体设计方案Fig.7 Design scheme of electromagnetic vibrating body

3 电磁振动体实验装置及能量回收电路

3.1 电磁振动体实验装置的研制

根据理论分析和方案设计，研制了如图8所示的电磁振动体实验装置。装置从上至下分别是：电磁阻尼器、弹性钢片和基座。作为能量回收的核心部件，电磁阻尼器具有如下技术特点：①采用了多组螺旋线圈串联而成的电磁感应系统，提高了输出电压的幅度；②采用磁能积最高的钕铁硼磁铁［19］，提高了单支线圈内的磁通量；③利用隔磁板分隔磁钢之间的磁场串扰，降低了磁损耗；④选用了无磁钛棒作为滑杆，减少了磁钢组的隔磁钢之间的磁场串扰，降低了磁损耗；⑤采用滑杆滚动摩擦的方式代替滑动摩擦，进一步减小了机械摩擦带来的能量损耗。表1列出了相关材料清单。

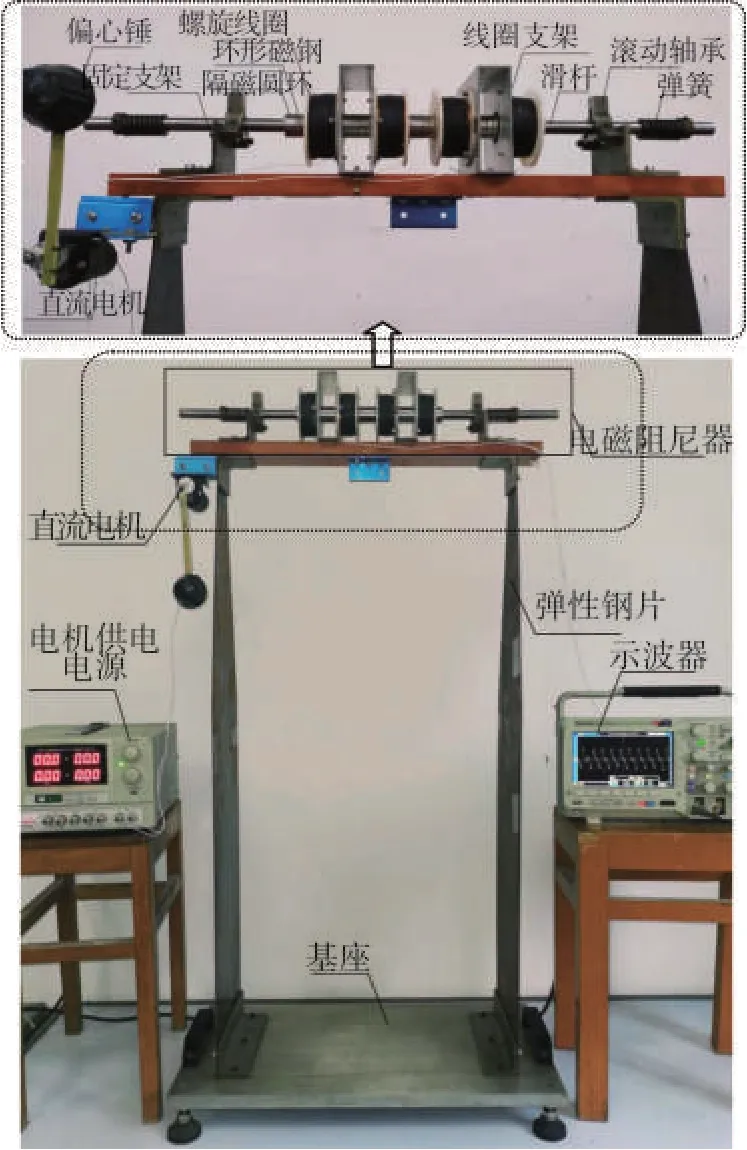
图8 电磁振动体实验装置Fig.8 Experimental device for electromagnetic vibrating body

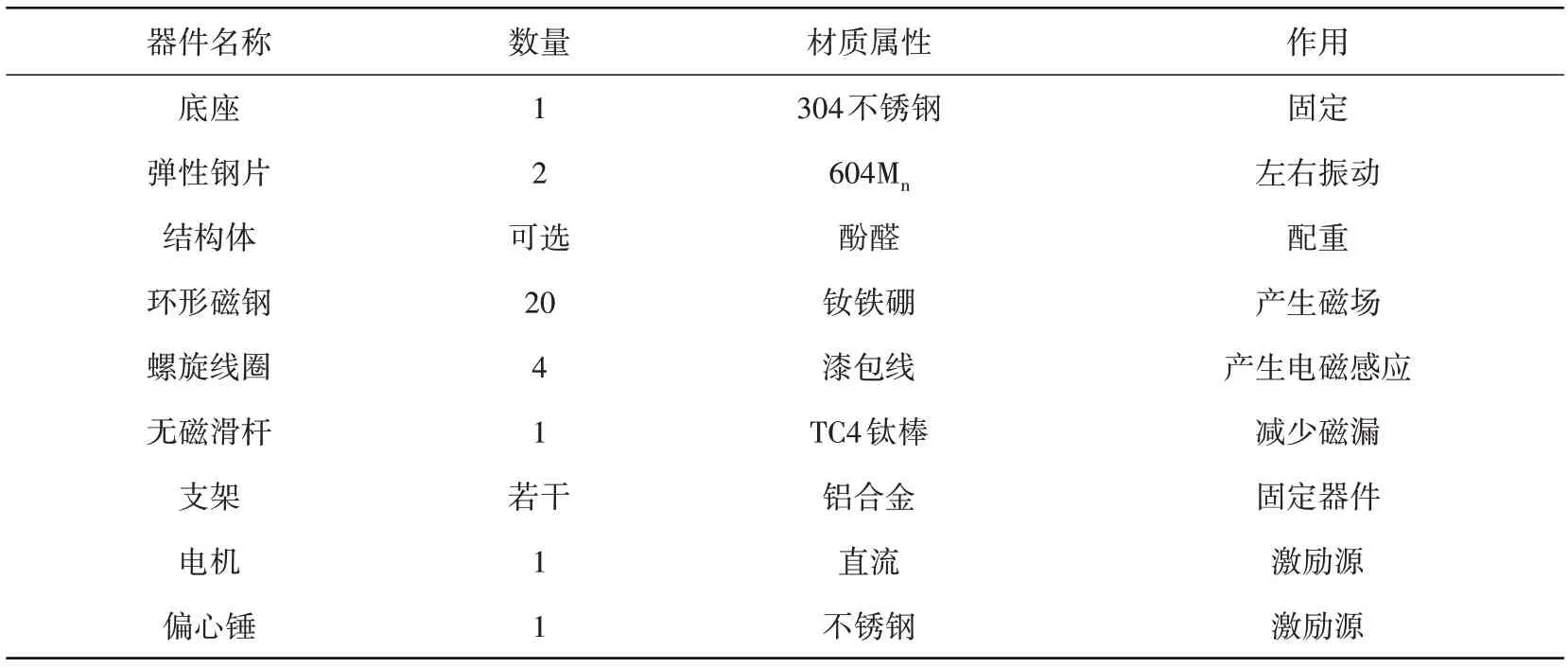
表1 电磁振动体器件Table 1 Electromagnetic vibrating body device

实验过程中，首先为带有偏心锤的直流电机提供电源，电磁阻尼器在偏心锤的作用下做水平方向振动。通过调节直流电机的供电电压值，使电磁阻尼器工作在频率约为1.6 Hz 的谐振状态，振动幅度约为14 mm。在此基础上，用示波器观察不同负载情况时负载上电压信号，实验结果如图9 所示。因此，①当负载阻值越大，负载两端的幅度也越大，最大幅度可超过30 V（见图9（d））；②当负载阻值越接近四个线圈的串联阻抗（约为406 Ω）时，负载功率越大，这符合最大功率传输定理（见图9（e））。

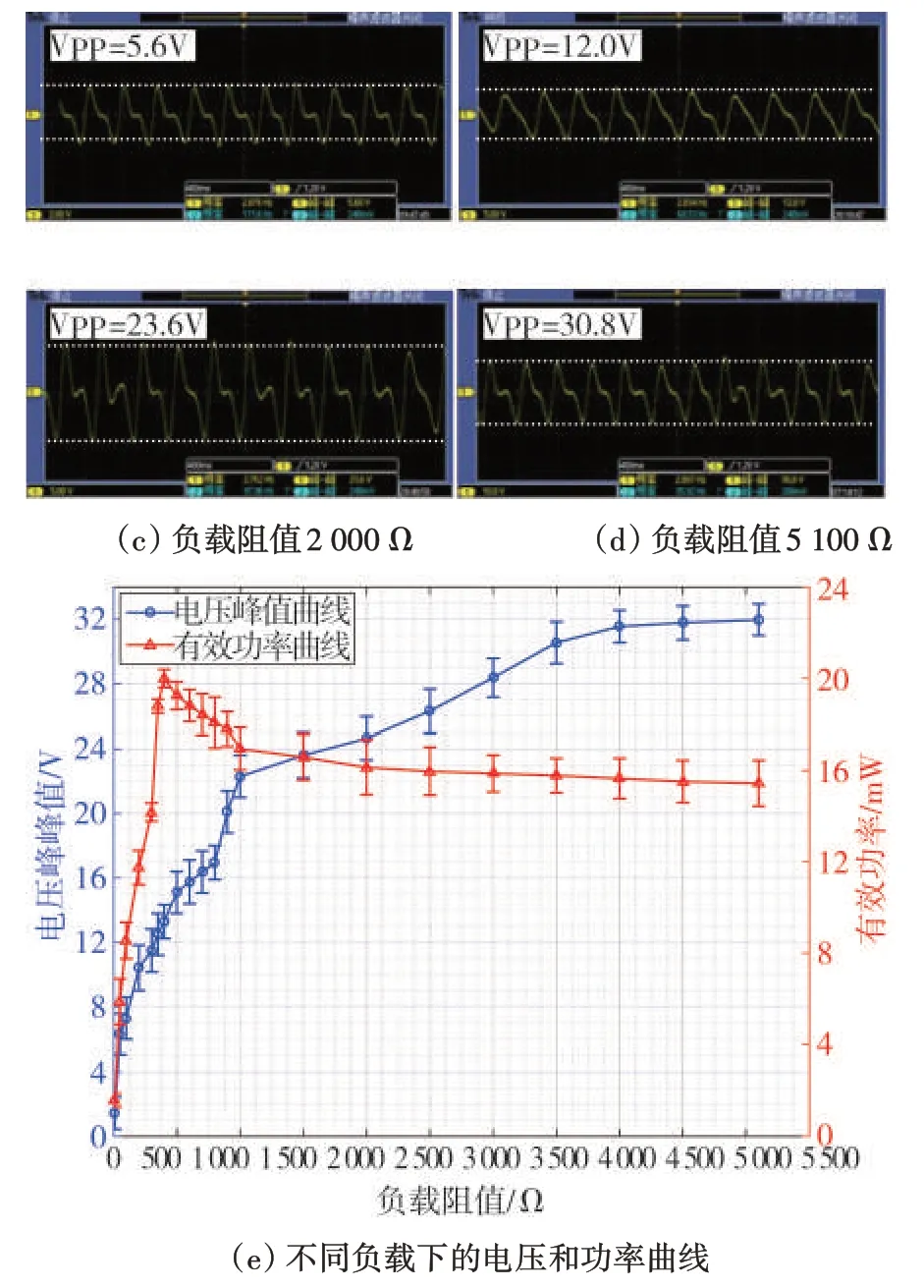
图9 电磁阻尼器带负载实验结果Fig.9 Experimental results of electromagnetic damper with load

3.2 能量回收电路的设计

由于电磁阻尼器产生的电压为非平稳交流信号，不能直接驱动供电电压为3.2～5 V 直流负载工作。因此，还需要进一步研究能量回收电路。能量回收电路主要包括全桥整流、降压稳压和充电管理［13，20－21］，如图10所示。作为电路的核心部分，在选择降压稳压芯片时应从三方面进行考虑：①输入电压范围大；②输出电压稳；③转换效率高。AD公司生产的DC/DC电压转换芯片LTC3388-3输入电压范围2.7～20 V，输出稳定的可调电压，且在负载电流大于1 mA时，其转换效率超过80%，较好地满足本系统功能需求。LTC3388-3电路输出接一容量较大的电容时（如3 300 uF），可以直接输出5 V电压，为低功耗设备持续供电。

图10 能量回收电路设计系统Fig.10 System of energy recovery circuit design

如果装置回收的能量用于锂电池充电，则需要充电管理模块。充分考虑锂电池预充电、充电和放电保护功能，充电管理电路选用单节锂电池充电芯片TP4054来实现。

当锂电池处于充电状态时，其两端的电压和电流如图11（a）所示，负载功率约为15.81 mW，这足以驱动结构健康监测系统中的无线传感器节点正常工作。为了直观地演示能量回收效果，我们在+5V 输出端接上手机和智能手环作为负载，手机和智能手环均能显示稳定的电池充电状态，如图11（b）和图11（c）所示。

图11 能量回收电路为多种外设充电实物图Fig.11 Physical diagram of the energy recovery circuit charging various peripherals

上述实验表明：系统不仅能够给包括锂电池、手环和手机在内的多种电器充电，还能给无线传感器节点供电；系统内置的锂电池还能够将毫安级电流存储起来，为其它种类的低功耗设备提供持续稳定的电能。

3.3 实验数据及结果分析

高层建筑的振动通常是由风荷载引起的，文献［22］表明高层建筑物在风力作用下的振动近似为简谐函数，风速的变化会引起高层建筑物振动幅值和频率发生改变。因此，通过改变实验装置中简易振动台的频率和振幅来间接模拟风速的影响，并开展相应的实验具有实际意义。

实验一：激励源频率对回收能量的影响

在实验过程中，调整直流电源电压值，同时改变结构体的重量（在结构体正下方增减电木块），控制结构体振幅不变，振动频率发生变化，以此来模拟风速引起的不同频率的振动环境。记录电磁振动体装置振动频率和收集能量电压的幅值。实验数据见表2，相应的频率-电压曲线如图12 所示（负载电阻为510Ω）。实验结果表明：当电磁阻尼器振动频率接近谐振频率（1.6 Hz）时，电压幅值最大。可见：当电磁阻尼器的振动频率与其固有频率一致时，收集的能量达到最大值。

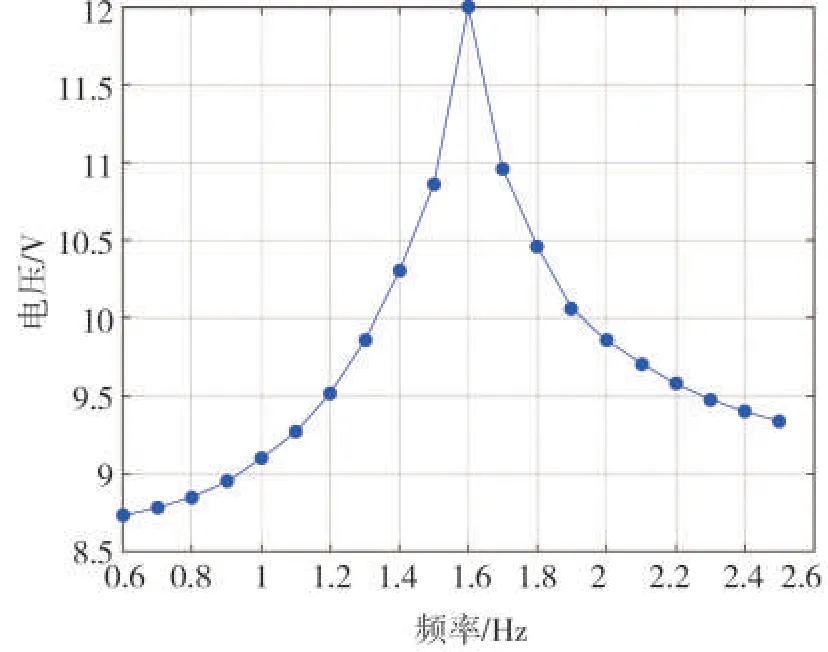
图12 振动频率与感应电压曲线Fig.12 Vibration frequency and induced voltage curve

表2 频率-电压数据Table 2 Frequency-voltage data

实验二：激励源振幅对回收能量的影响

采用与实验一类似的调整方法，改变结构体重量，同时调整直流电源电压值，保持结构体工作在谐振频率不变，其振动幅度变化着，以此来模拟风速引起的不同振幅的振动环境。记录电磁振动体装置振动幅度和收集能量电压的幅值。实验二的数据结果见表3，相应的振幅-电压曲线如图13 所示（负载电阻为510 Ω）。

表3 振幅-电压数据Table 3 Amplitude-Voltage Data

图13 的振幅-电压曲线图表明：电磁振动体装置在共振频率下，感应电压与振动幅度呈单调递增关系。当振动振幅增加到一定幅值时，电压增长速度变慢。这是因为弹簧工作在非线性区而引起的能量损耗增大所致；同时，振幅的增加也会引起钛合金棒与轴承之间的摩擦能耗增加，导致能量转换效率有所降低。

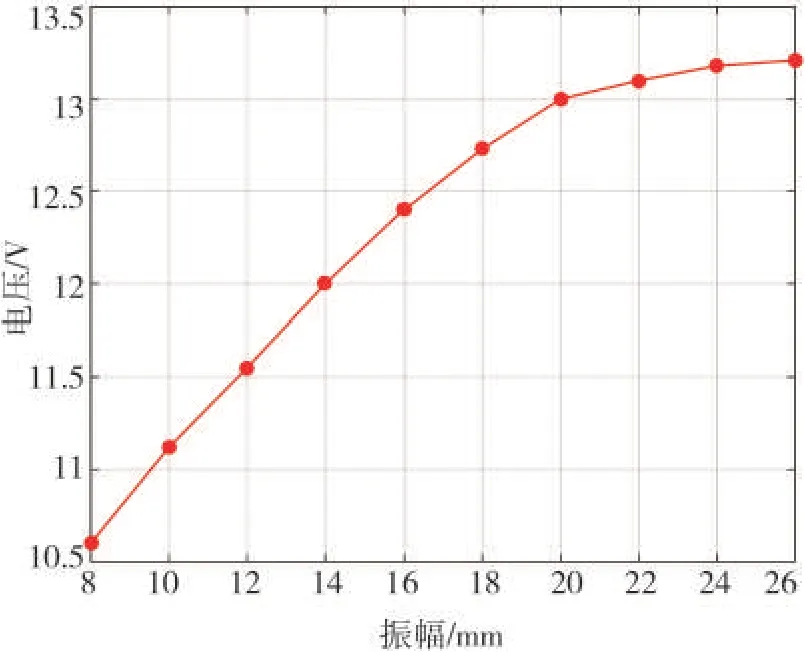
图13 振动幅度与感应电压曲线Fig.13 Vibration amplitude and induced voltage curve

4 总结

针对高层建筑物等水平振动环境的能量回收问题，本文设计了一种基于电磁阻尼的振动能量回收装置。其中：基于滚动轴承的电磁阻尼器减小了滑动摩擦带来的能量损耗；多只线圈串联的组合方式提高了机械能转换为电能的效率；低功耗稳压电路和充电管理电路解决了电能的转换和存储难题。实验研究表明：该装置产生的电压峰值可达31 V，最大输出功率达20 mW，经过高效电压转换之后，不仅能够为结构健康检测系统供电，而且可以为包括锂电池、手机和智能手环等储能设备充电。如何自动地调节电磁阻尼器的谐振频率，使之与环境的振动频率一致，从而更高效率地收集振动能量，以及设计更加高效的能量回收电路，这将是我们下一步研究的重点。