反复荷载下型钢混凝土柱受扭损伤试验研究

袁军海，邵永健，盛炜仲，李国建

（1.苏州科技大学土木工程学院，江苏苏州 215011；2.中亿丰建设集团股份有限公司，江苏苏州 215131）

引言

工程结构中型钢混凝土结构的应用愈加广泛，型钢混凝土结构具有优异的抗震性能、良好的耐火性能和耐久性能，并且具有良好的经济效益，是多地震国家和地区的首选结构形式。在实际工程中，构件受扭情况不少，但是单独受扭矩作用的结构不多，大多数都处于复合受扭状态下。与此同时，随着型钢混凝土研究的不断深入和工程应用的不断增多，研究型钢混凝土构件和结构在地震作用下的复杂受力行为、损伤演化规律和破坏过程显得尤为重要。

国内学者针对构件的抗震性能进行一系列研究，文献［1］对不同配钢形式的圆截面型钢混凝土巨型柱进行试验，结果表明H 型钢混凝土巨型柱表现出良好的强轴方向性能。文献［2］进行了高轴压比下型钢混凝土柱抗震性能试验，结果表明高轴压比试件会使延性性能和耗能能力变差。文献［3］对7个弯扭型钢混凝土柱进行抗震性能试验，研究表明扭弯比对于型钢混凝土柱抗震性能有显著的影响，型钢混凝土柱抗弯承载力及其变形能力在弯扭复合作用下均降低，决定构件破坏形式是扭弯比的大小。文献［4］对7个SRC柱进行了弯矩和扭矩成比例加载的低周往复试验，研究表明影响型钢混凝土柱抗震性能的主要因素是扭弯比。文献［5］通过对12 根复合受扭试件的抗震性能试验研究表明，十字型钢混凝土受扭试件比H 型钢混凝土试件具有更好的延性。文献［6］通过3个复合受扭型钢混凝土柱的抗震性能试验研究，揭示了轴压比和扭弯比对复合受扭型钢混凝土柱抗震性能的影响。文献［7］对不同配箍形式型钢混凝土柱的抗震性能试验表明，配箍形式对SRC 柱滞回性能有明显影响，八角复合箍的配箍形式提高了试件延性。国外相关学者针对地震损伤进行相关研究，BANON 等［8］、STEPHAL 等［9］、CHUNG 等［10］都提出以变形为参变量的损伤模型和GOSAIN 等［11］提出基于能量吸收和耗散的损伤评价模型；PARK 等［12］首先建立构件双参数累积损伤模型，之后学者也均沿用其思路。文献［13］进行框架梁的损伤试验研究。但目前对于型钢混凝土柱的损伤研究很少。

本文通过12根复合受扭柱的受力损伤试验研究，研究了在低周反复荷载下，型钢混凝土柱的破坏形态、裂缝开展和分布规律，揭示其损伤演变规律以及影响因素，进一步完善型钢混凝土复合受扭构件设计理论，并为实际工程应用提供技术支撑。

1 试验概况

1.1 试件设计及制作

共设计制作了11根型钢混凝土柱试件和1根钢筋混凝土柱对比试件，考虑了柱截面配钢形式、轴压比、扭弯比、混凝土强度等级、配箍率和配钢率6个变化参数，具体参数见表1。模型以1/2缩尺设计，试件的截面尺寸为300 mm×300 mm，柱高900 mm，柱中H1 是HW150×150×7×10，H2 是在翼缘焊接有84 mm×8 mm 的钢板，而十字型钢是2 个HN200×100×5.5×8 剖切焊接而成，混凝土采用C35 和C40，试件几何形状、截面形式和配钢形式如图1所示。钢材材料性能见表2。

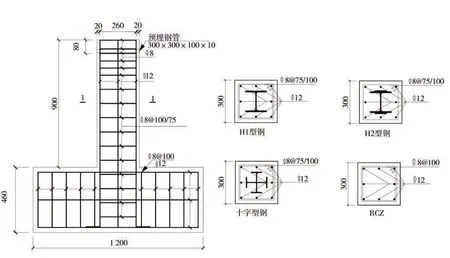
图1 试件的几何形状和截面形式Fig.1 Geometric shape and cross section form of the specimen

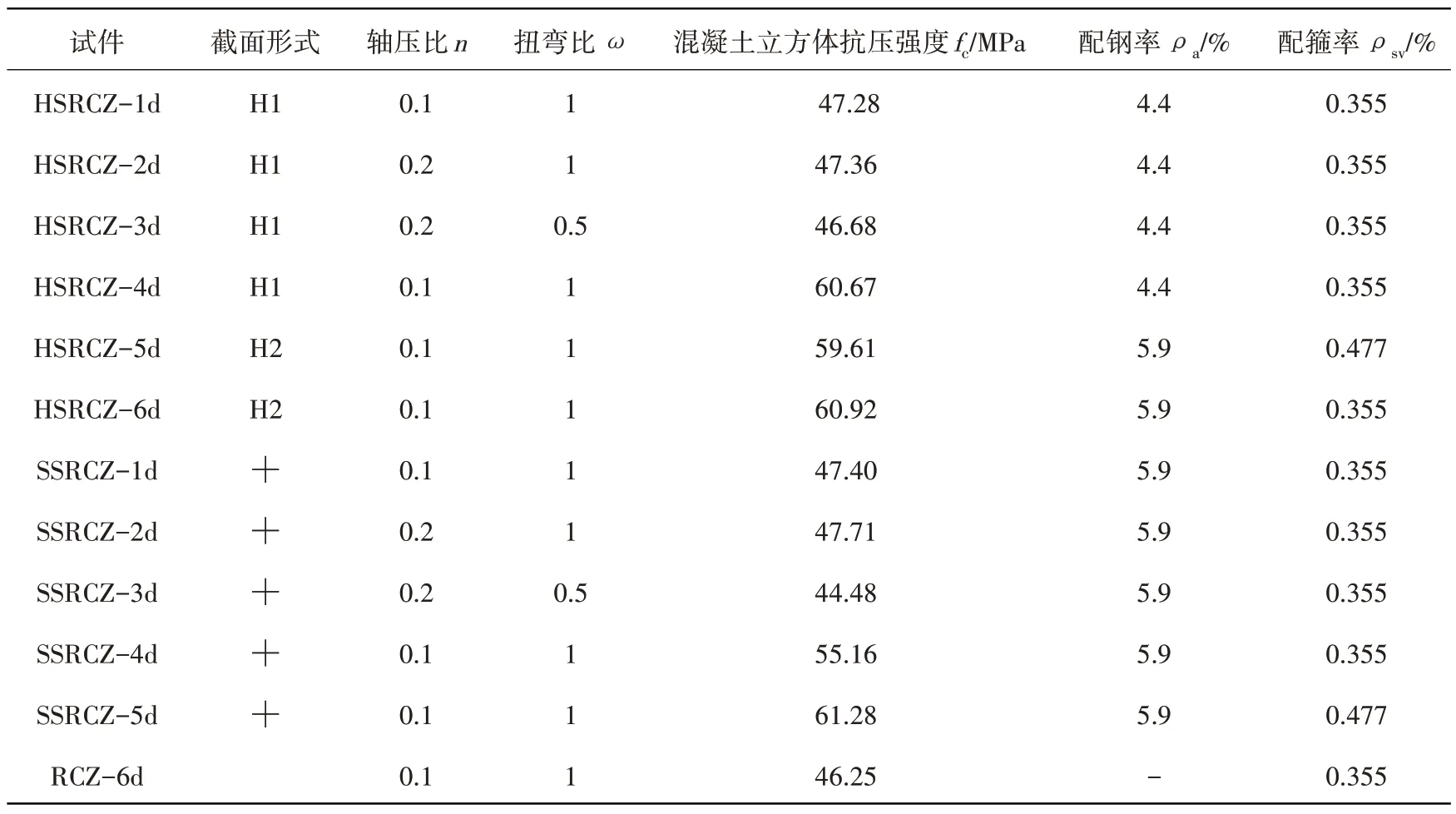
表1 试件设计参数Table 1 Specimen design parameters

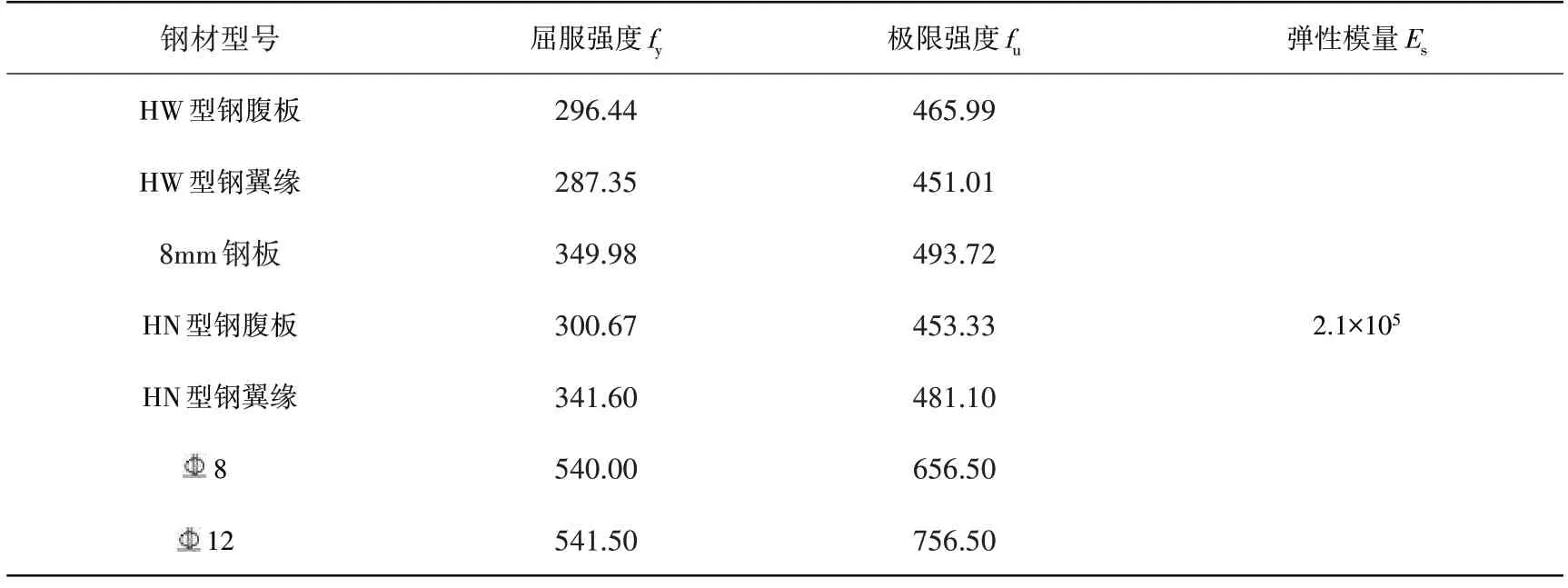
表2 钢材材料性能Table 2 Materialperformance of steelMPa

1.2 加载方案

加载装置如图2 所示，采用竖向千斤顶施加轴向力，采用伺服作动器施加水平往复力，试件加载面示意图如图3所示。

图2 试验加载装置Fig.2 Test setup

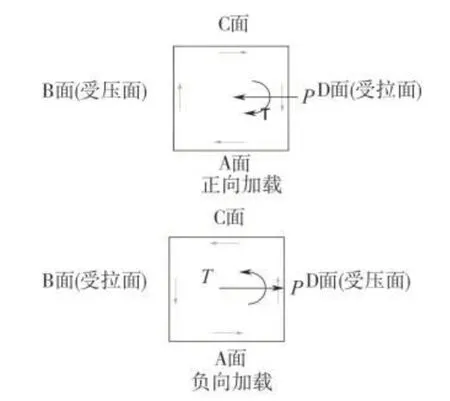
图3 加载面示意图Fig.3 Diagram of loading surface

整个加载过程采用位移控制，加载时先对试件进行预加载，检查装置测量无误后进行正式加载。正式加载时先按预定荷载施加竖向轴力，并保持不变。然后水平方向逐级施加位移，在试件开裂前，每级位移加载2 mm，往复循环1次；开裂后，每级位移加载4 mm，往复循环1次；试件屈服后，每级位移加载10 mm，往复循环3次，直至试件承载力下降至最大水平荷载的85%时，结束试验。加载历程如图4所示。

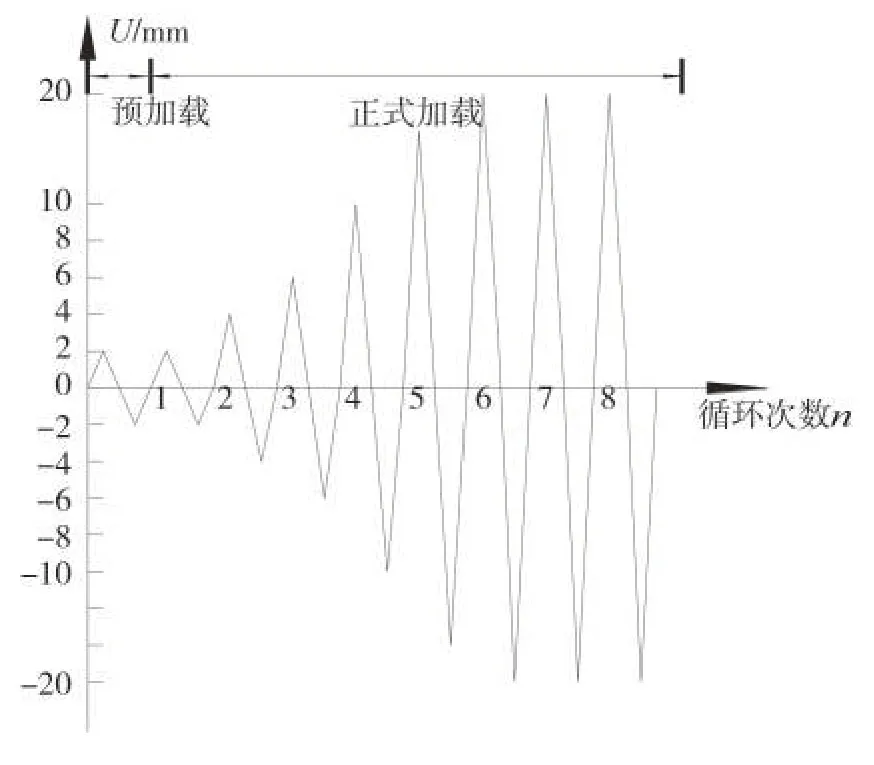
图4 加载历程Fig.4 Loading history

1.3 测点布置和测试内容

测试的内容包括：（1）柱顶水平荷载P，由伺服作动器系统反馈；（2）试件水平位移，通过电子位移计量测，如图5 所示；（3）试验过程中各部位应变值，通过应变片测量。在其表面距离基础顶面150 mm 布置4 片柱身混凝土应变花；纵筋应变片贴在基础以上100 mm和300 mm位置处，在离基础上表面近的4根箍筋贴16片箍筋应变片，每根箍筋每个面贴一片；型钢在距离基础上表面100 mm、300 mm 位置处布置应变花和应变片，H 型钢腹板A 面和C 面布置应变花，翼缘各一片应变片，十字型钢2 个应变片和6 个应变花，具体布置如图6所示。

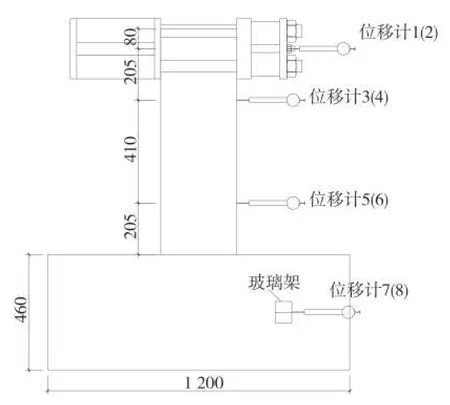
图5 位移计布置图Fig.5 Displacement meter layout

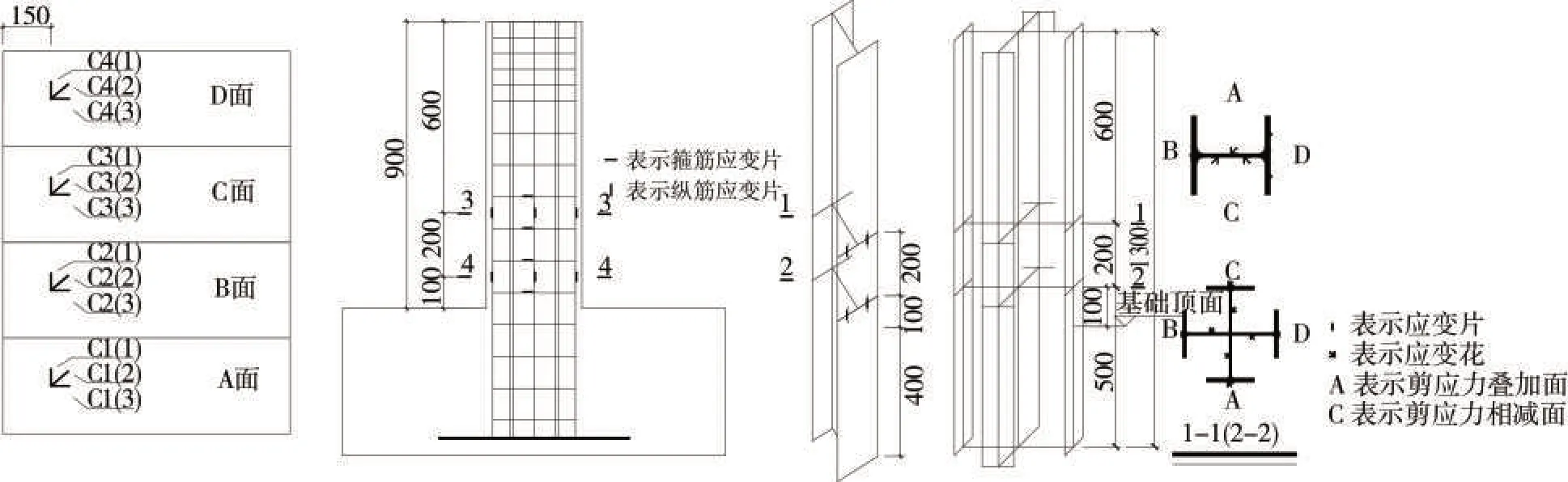
图6 应变片布置图Fig.6 Strain gauge layout

2 试验现象与破坏形态

为方便分析，试件各表面按照D、C、B 和A 进行编号，试件的最终破坏形态按照这个顺序如图7 所示，A面为剪力叠加面，B 面为弯曲承压与扭矩叠加面，C 面为剪力相减面，D 面为弯曲承拉与扭矩叠加面，其各面展开图如图8所示。低周反复荷载下，型钢混凝土柱破坏特征：首先，所有试件A面均出现初始斜裂缝，随后B、C 和D 面均也相继出现，随着位移幅值的增大，A、B、C 和D 面的斜裂缝不断增多，并且大都分布在柱的中部，不断延伸形成贯通斜裂缝并成一定角度。位移幅值进一步加大，构件逐渐屈服，各表面逐渐形成交叉状的贯通斜裂缝。构件屈服之后，进行循环加载，此时的贯通裂缝不断增多，且各面贯通裂缝相连形成螺旋贯通缝。继续加载至峰值荷载时，裂缝间混凝土开始起皮并伴随有混凝土脱落。继而试件破坏，此时，混凝土的脱落情况加重，受扭现象明显，承载力开始退化，表面形成了大的主裂缝，构件破坏严重有大片的混凝土脱落，内部钢筋外露。

图7 试件最终破坏形态Fig.7 Ultimate failure pattern of the specimens

图8 裂缝展开图Fig.8 Crack expansion plane

分析试验现象和破坏形态可知：在本文试验参数范围内，各试件最终破坏形态均为扭型破坏。

3 损伤分析

3.1 损伤演变分析

结构损伤程度一般采用损伤指数D来表示，D可以通过累积损伤模型计算求得，其取值范围为（0，1）。依据能量耗散原理，以结构在无损伤状态下外力所做的功为初始标量，建立了混凝土结构的整体损伤模型。本文基于此基础之上将构件当做一个系统，建立累积损伤模型如图9 所示求得型钢混凝土柱的损伤指数D［14］。

在理想无损状态下，外力所做的功为Wi；在损伤状态下，外力所做的功转化为：弹性变形能Wei、塑性变形能Wpi和损伤耗散能WDi，即：

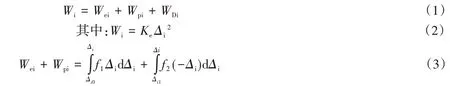
式中：Ke为结构的初始加载刚度；Δi是第i次循环正负向最大变形（假设两个方向的变形相等），Δi0第i-1次循环负向卸载为零时的残余变形；Δi1为第i次循环的正向卸载为零时的残余变形。

综上所述，损伤指数D的公式为：

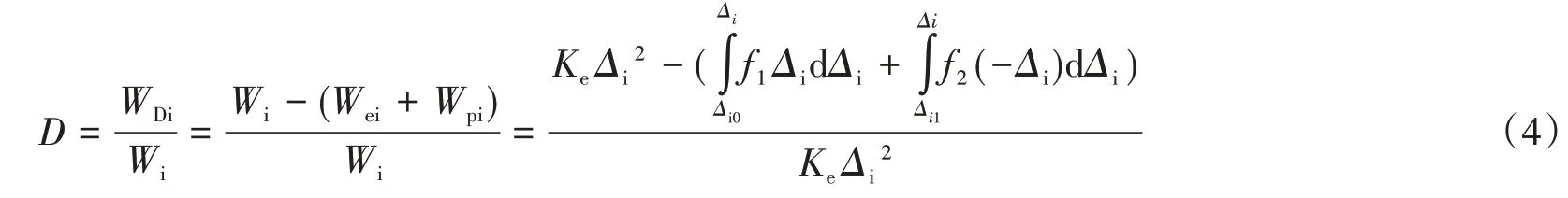
根据图9中各面积可表示为：

图9 试件第i个循环的受力状态Fig.9 Ith cycle’s stress state of the specimen

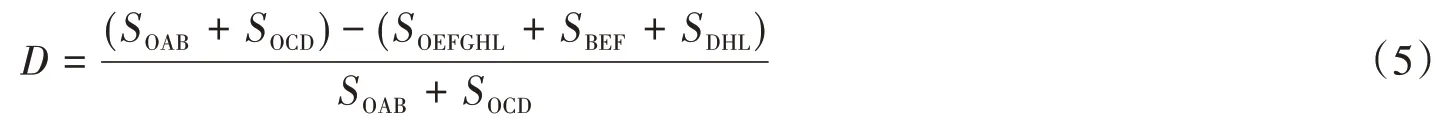
根据试验所得各试件的扭矩-扭率滞回曲线，通过式（5）计算出型钢混凝土柱累积损伤指数见表3。由表3可知：在低周反复荷载作用下，型钢混凝土柱极限荷载破坏时的损伤指数处于0.884～0.926，钢筋混凝土柱破坏时的损伤指数为0.904。

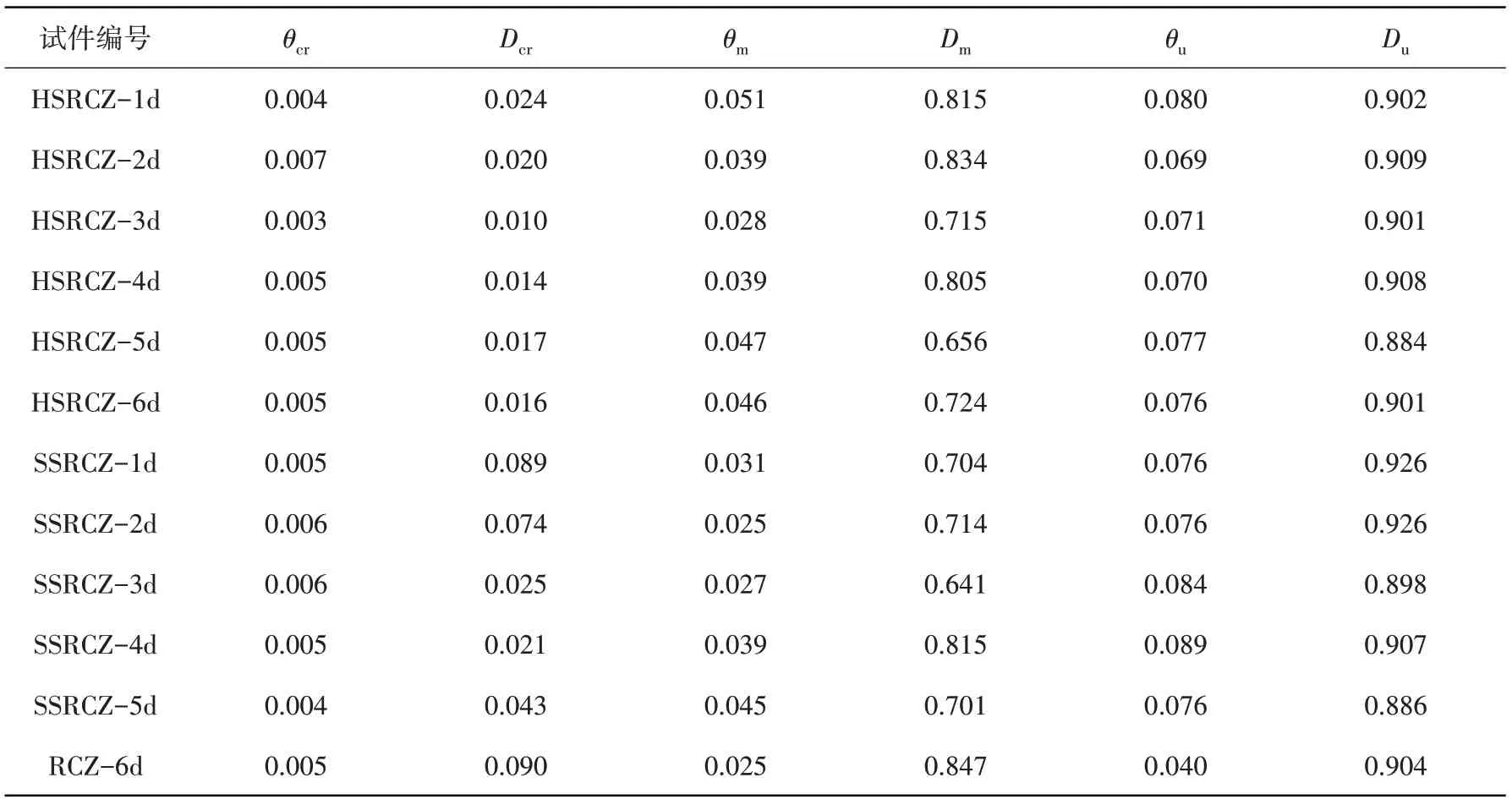
表3 各试件累积损伤指数Table 3 Cumulative damage index of the specimens

12 个试件的损伤指数曲线如图10 所示。根据图10 和试验相关现象以及破坏形态，所有试件的累积损伤可分为3个阶段。加载初期，试件未出现裂缝，其处于弹性阶段，损伤指数接近于0，此时试件处于无损状态；试件开裂后，其处于弹塑性阶段，损伤指数呈线性增长，此时裂缝开始增多，随着扭率的增大，损伤指数不断增加，但增长速度趋于减缓；加载后期，试件处于破坏阶段并且进入大变形，损伤指数上升趋于平缓。当损伤指数接近0.90 左右时，试件因受扭破坏严重而基本破坏。与型钢混凝土柱相比，钢筋混凝土柱其损伤指数增长速度较快，相同位移荷载下，钢筋混凝土柱的累积损伤指数均高于型钢混凝土柱，并且试件过早达到最大损伤，而型钢混凝土柱累积损伤较慢，这说明型钢混凝土柱可以很好减缓内部损伤。

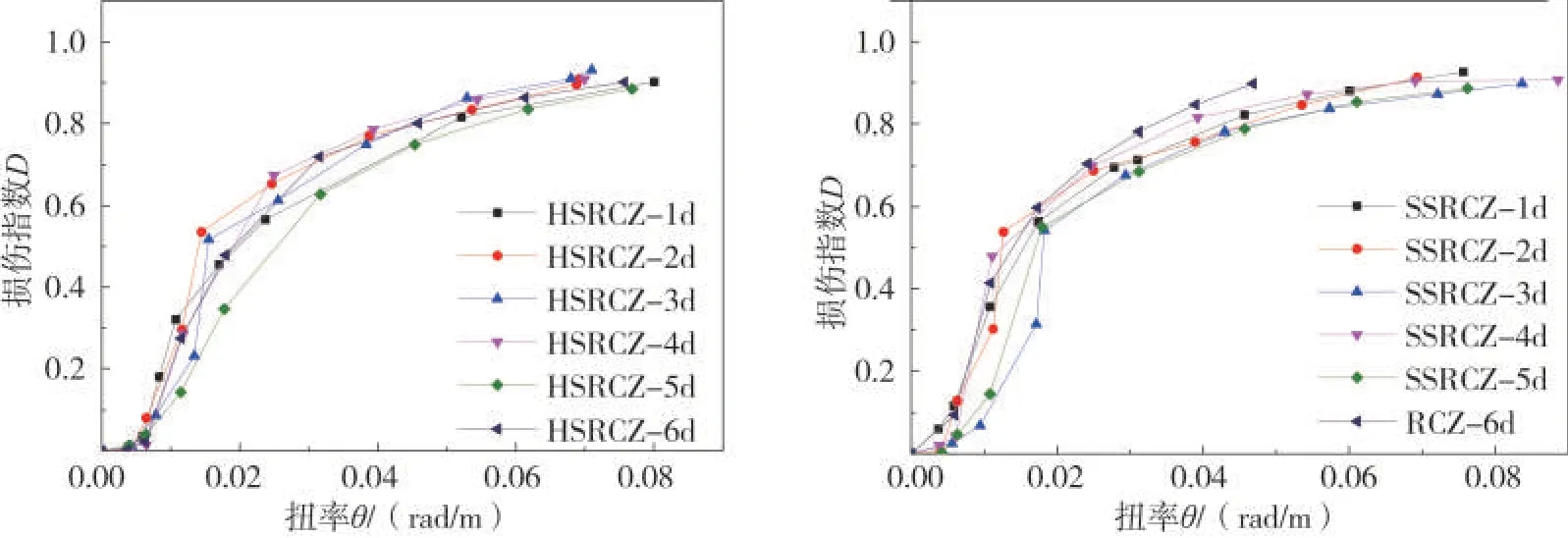
图10 累积损伤曲线Fig.10 Accumulated damage curves

3.2 累积损伤的影响因素分析

（1）配钢形式的影响

图11（a）给出了不同的配钢形式对试件损伤指数曲线的影响。结合图和表3可知：十字型钢混凝土柱和H 型钢型混凝土相比，峰值时损伤指数增大了12.6%。这是因为前期加载过程中，试件仅由外层的混凝土参与受扭，损伤基本一致，进入弹塑性阶段，内部的钢筋和型钢参与受扭，由于不同的型钢形式对混凝土约束不同，从而导致受扭能力也有所不同，十字型钢能承受较大的扭矩自然吸收更多的能量，损伤耗散能量越多，这使得其承受损伤越大。图11（b）钢筋混凝土柱与十字型钢混凝土柱相比，在扭率到达0.04 rad/m，十字型钢混凝土柱损伤指数比钢筋混凝土柱降低了22.1%，同时，钢筋混凝土柱就已经到达累积损伤最大状态，所以内配型钢不仅能够提高试件的抗扭能力，而且能够减缓其损伤演变速度。

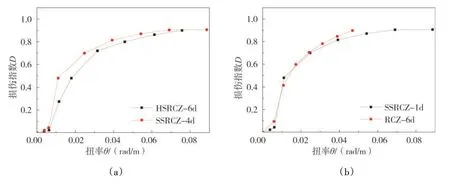
图11 不同配钢形式的影响Fig.11 Influence of different steel form

（2）轴压比的影响

由图12和表3可知：随着轴压比从0.1上升至0.2，H型钢和十字型钢混凝土柱开裂时损伤指数分别降低了16.7%和16.8%，这与试验现象得出的结论相吻合（加载前期轴压比的增大可抑制斜裂缝的产生）。轴压比大的H 和十字型钢混凝土柱峰值时损伤指数分别增大了2.3%和1.4%，这说明轴压比的增大可以抑制弹性阶段的损伤，但一旦混凝土开裂且裂缝增多，其释放的能量就越多，从而造成后期试件损伤严重。十字型钢对混凝土的约束优于H型钢，与混凝土协同工作抑制内部的损伤，以致峰值时损伤指数变化更小。

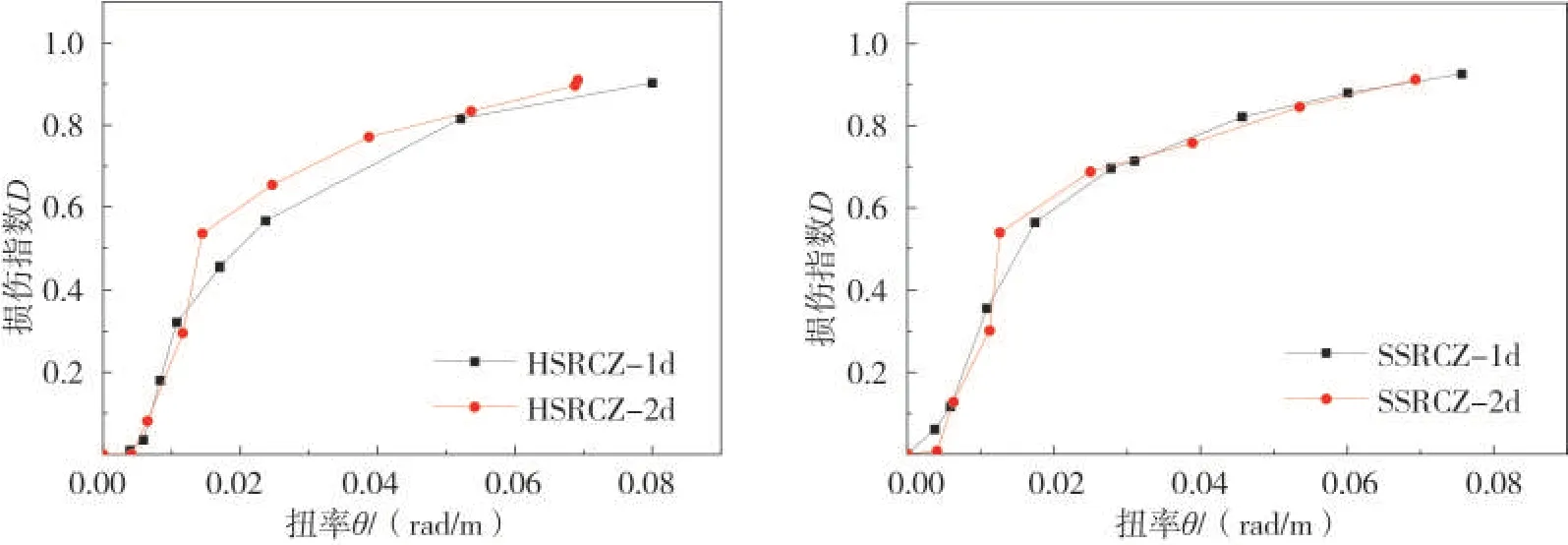
图12 不同轴压比的影响Fig.12 Influence of different axial compression ratio

（3）扭弯比的影响

根据试验数据分析得到扭弯比规律如图13 所示，根据图和表3，HSRCZ-3d 与HSRCZ-2d 相比，SSRCZ-3d 与SSRCZ-2d 相比，扭弯比从1 减少至0.5，H 型钢混凝土柱峰值时损伤指数降低了14.3%，十字型钢混凝土柱峰值时损伤指数降低了10.2%。这说明扭弯比越大，其损伤越严重，扭矩占比较大，从而导致试件内部混凝土的微裂缝产生的愈多愈快，最后形成宏观上试件表面的裂缝，试件的扭转破坏更严重。

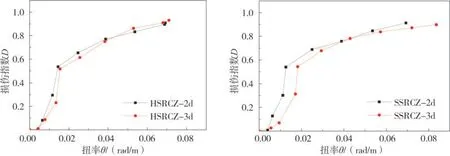
图13 不同扭弯比的影响Fig.13 Influence of different torsion-bending ratio

（4）混凝土强度的影响

图14 给出了不同混凝土强度对损伤指数曲线的影响。根据图表数据分析可知：HSRCZ-1d 与HSRCZ-4d相比，SSRCZ-1d与SSRCZ-4d相比，混凝土强度等级提高，损伤指标变化幅度在1%左右，这是由于混凝土强度高的试件在弹性阶段由外部混凝土受扭，其吸收能量储存在试件中，开裂后释放能量导致内部损伤变大，后期混凝土破坏严重退出受扭工作，混凝土强度等级不同导致损伤指数变化差异较小。这说明混凝土强度的变化对试件损伤程度影响偏小。

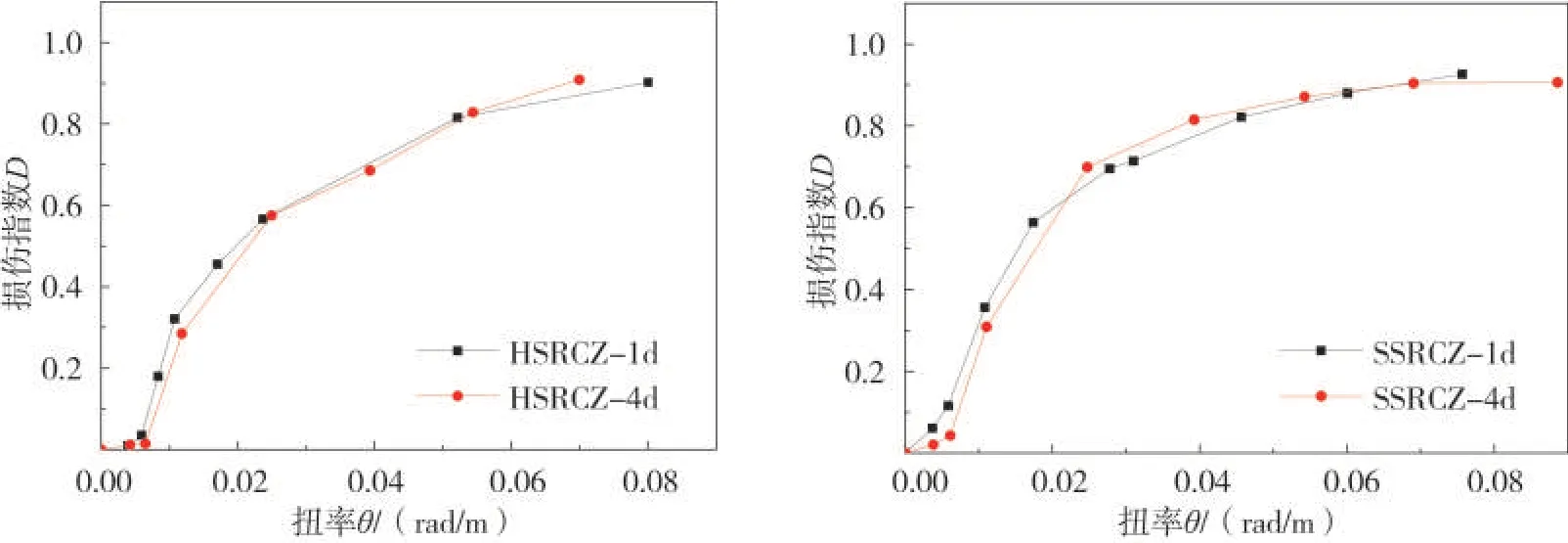
图14 不同混凝土强度的影响Fig.14 Influence ofconcrete strength

（5）配箍率的影响

图15 给出了不同配箍率对损伤指数曲线的影响。根据图表数据分析可知：随着箍筋间距从100 mm 减少至75 mm，H 型钢混凝土柱峰值时损伤指数降低了9.4%，十字型钢混凝土柱峰值时损伤指数降低了14.0%，说明加密箍筋可以有效的约束内部混凝土，抑制内部裂缝的发展。总体而言，在低周反复荷载下，配箍率越高对混凝土约束作用越强，越能抑制内部损伤的发展，提高配箍率对试件损伤指标降低较大。

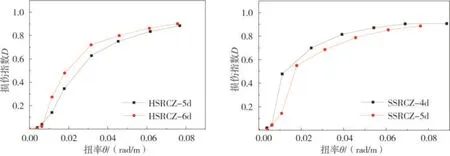
图15 不同配箍率的影响Fig.15 Influence ofstirrup ratio

（6）配钢率的影响

不同配钢率对损伤指数曲线的影响如图16 所示。根据图表数据分析可知：随着配钢率从4.4%升至5.9%，峰值时损伤指数降低了9.5%，试件前期损伤指数曲线基本一致。这是由于后期外部混凝土损伤严重基本退出工作，由内部型钢承担受扭，在型钢翼缘焊接钢板提高了试件的刚度，从而略微降低其内部累积损伤。

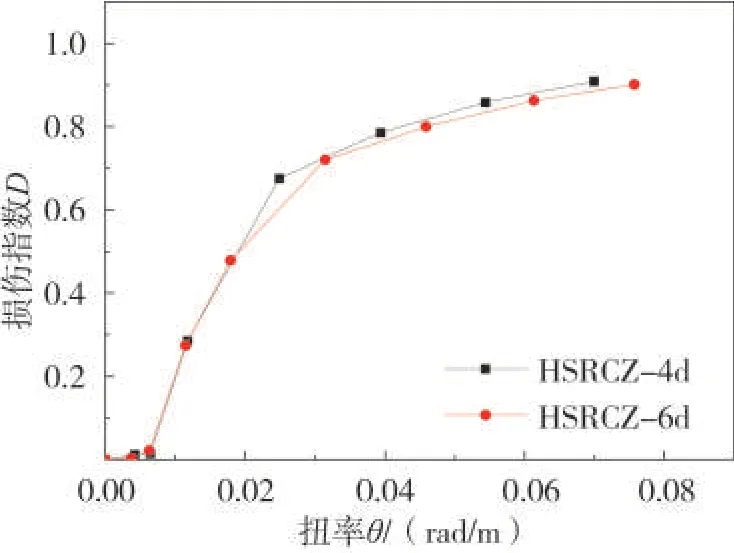
图16 不同配钢率的影响Fig.16 The influence ofreinforcement ratio

4 结论

通过11个型钢混凝土柱和1个钢筋混凝土柱的低周反复荷载试验和损伤分析，得到结论如下：

（1）本文试验参数范围内，型钢混凝土柱累积损伤过程可分为3个阶段：弹性阶段、弹塑性阶段和破坏阶段。试件累积损伤的规律：弹性阶段损伤基本为0，试件没有肉眼可见宏观意义上的裂缝；弹塑性阶段试件已开裂，其损伤迅速增大；在后期破坏阶段，损伤开始趋于平缓。最终破坏时的累积损伤指数为0.884～0.926。

（2）本文试验参数范围内，试件达到承载力峰值时，内配十字型钢相比H 型钢损伤指数增大了12.6%。扭弯比从1减少至0.5，配H 和十字型钢试件损伤指数分别降低了14.3%和10.2%。箍筋间距从100 mm 降至75 mm，配H和十字型钢试件损伤指数分别降低了9.4%和14.0%。内配十字型钢与不配型钢相比，试件破坏时损伤指数可降低22.1%。适当配置型钢、降低扭弯比和提高配箍率达到降低损伤程度的作用。

（3）本文试验参数范围内，轴压比从0.1上升至0.2，试件开裂时，配H型钢和十字型钢试件损伤指数分别降低了16.7%和16.8%，试件达到承载力峰值时，损伤指数分别增大了2.3%和1.4%。配钢率从4.4%升至5.9%，配H型钢试件损伤指数降低了9.5%。混凝土强度提高，损伤指标变化幅度仅在1%左右。说明适当小范围提高轴压比仅对前期损伤指数有降低作用，相反提高配钢率仅对后期损伤指数起降低作用，而混凝土强度对降低损伤指标影响几乎没有。