基于图像压缩的震损结构三维模型快速重建方法

霍林生，王忆泽，白晓煜

（大连理工大学海岸和近海工程国家重点实验室，辽宁大连 116024）

引言

地震是一种有着巨大破坏力的自然灾害，而每年在全世界范围内都会发生大量的地震。地震造成的人员伤亡和建筑物破坏会带来巨大的损失［1－2］，而建筑物的倒塌和破坏是造成生命和财产损失的主要原因，因此地震应急要求地震发生后在第一时间进行震损建筑的可居住性和安全性评估［3］。

目前利用图像进行震损结构的评估主要有两种方式：一种是直接利用二维的震害图像［4－6］；另一种是基于图像的三维重建技术［7－8］。二维图像虽然信息可能不够全面，但是由于图像获取的便利性，专家们也是进行了很多的研究，其中在基于结构震后损伤图像方面主要包括混凝土结构的检测与自动评估。ZHU 等［9－10］和GERMAN 等［11］对基于图像的震后结构检测和结构整体安全评价进行一系列研究，使震损评估更加智能化；韩建平等［12］利用图像处理方法对结构模型位移测量并且其提出的方法可以较好得识别结构的模态参数，这对新型结构状态评估方法具有启发意义。除了上述建筑结构损伤评估，桥梁结构损伤评估也有相关研究［13］。

相较于二维的震害图像而言，基于图像的三维重建方法生成的三维模型使得结果更为直观和精确。因此越来越多的专家把三维重建法应用到结构损伤评估中，其中较多的是裂缝检测。MATTHEW 等［14］提出了一种针对混凝土裂缝三维模型的检测算法；JAHANSHAHI等［15］基于图像和神经网络把三维重建技术应用到裂缝检测中；另外对于震损结构的三维重建技术目前也有相关研究，霍林生等［16］提出了使用图像三维重建方法对实际震损墙体建模的方法。虽然基于图像的三维模型重建法在震损评估中的应用已经得到了验证，但是对于大尺寸结构，为了保证精度必须采集更多的图片和更高的分辨率，导致的建模耗时过长制约了技术的应用发展。因此本文利用主成分分析算法压缩拍摄的图像，然后对图像中的目标物三维重建达到减少结构建模时间的目的。

1 基于主成分分析的图像压缩算法

1.1 主成分分析算法的原理

卡尔·皮尔逊在1901年提出主成分分析算法（Principle Component Analysis，PCA）［17］，主成分分析算法的核心思想是将n维的数据特征映射到k维上（k＜n），映射后的k维特征是全新的正交特征。这k维特征称为原数据的主成分，是重新构造出来的k维特征，从而达到数据的降维和特征的提取。利用主成分分析算法对图像进行压缩的原理为：假设有一个数据集S包括m个n维样本，即：

将数据集S以矩阵的形式表示，则矩阵的每一行为一个样本，每一列为一个维度，即S∈Rm×n Rm×n，将S的每一行进行零均值化，即减去这一行的均值：

式中：C∈Rm×n。计算得到协方差矩阵C的n个特征向量和特征值，将特征值从大到小排列，取前k个特征值对应的特征向量组成转换矩阵P，并且这k个特征向量相互正交。压缩后的矩阵为：

综上可知：PCA 算法本质上是将方差最大的方向作为主要特征，并且由于特征向量的正交性，使数据在不同正交方向上也没有相关性，根据PCA算法的特点可以很好地将其应用在图像的压缩中。

1.2 主成分分析算法在图像压缩中的应用

根据上述步骤，利用PCA 算法对混凝土块的图像进行压缩。以一个混凝土试块的图像为例，拍摄的所有图像分辨率为768×1 024，首先将每张图像分解为N张分辨率大小为K的子图像，此处K值是影响图像压缩效果的重要变量，K值越大，N越小，丢失的特征也越多。在实验中，K值分别取K=2、K=3和K=4，N相应变为N=196 608、N=87 495和N=49 216。其次计算每张子图像的平均值：

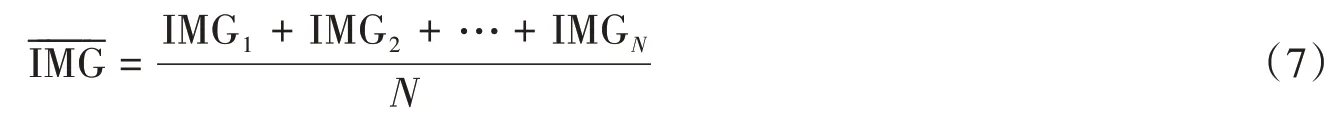
式中：IMGN代表子图像；N代表子图像数量。其次将N张子图像减去平均值图像得到N张新的子图像IMGS：

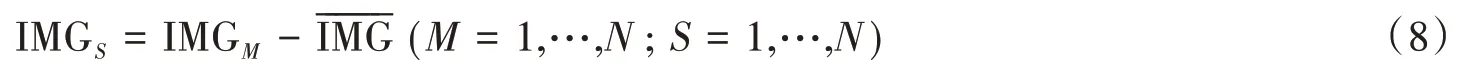
然后计算出新子图像的协方差矩阵R，其公式定义为：

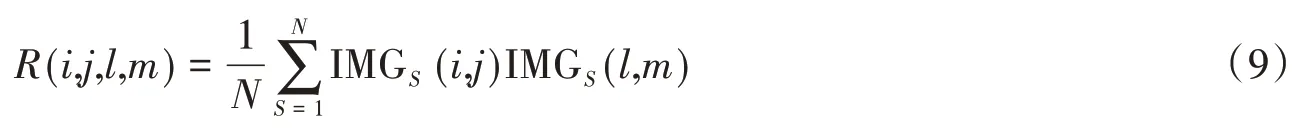
式中：i，j，l，m代表元素在图像中的位置。

由R得到转换矩阵，将子图像与转换矩阵点积，压缩后的图像见图1。可以看出：随着K值的增大，压缩后的图像清晰度将会降低。

图1 混凝土块原始图像和压缩后的图像Fig.1 Original image of the concrete block and its compressed images

2 基于图像压缩三维模型重建技术

从多幅二维图像中恢复重建结构三维模型的问题，在近几十年得到大量而深入的研究，尤其是从摄像机运动中恢复重建三维场景（structure from motion，SFM）［18］。SFM 算法能够从未标定的图像中检测特征点，对多幅图像中的特征点匹配，恢复出结构的三维模型，本文提出的基于图像压缩的三维模型重建方法的基本思路如图2所示：（1）围绕目标物且尽量保持相机在同一水平面以特定角度拍摄图像［19］；（2）对采集的图像用主成分分析算法进行压缩处理；（3）提取和匹配二维图像中的特征点来标定相机的位置，并由此来重建出三维模型的稀疏点云数据；（4）使用MVS算法稠密化点云；（5）使用泊松表面重建算法构建三维模型的表面；（6）对模型表面纹理映射，生成真实感强的三维模型，完成三维模型的重建。

图2 基于图像压缩三维模型重建技术流程图Fig.2 Flow chart of 3Dmodel reconstruction technology based on image compression

2.1 运动恢复结构

运动恢复结构算法（Structure From Motion，SFM）是三维重建技术的核心。该算法是对采集到的图片进行特征匹配，标定相机，重现相机的运动，恢复场景的三维结构，由此来实现三维重建。算法的基本思路是：首先利用尺度不变特征变换（scale-invariant feature transform，SIFT）方法提取图像的特征点［20］，用最优搜索算子对任意两张图像进行特征点匹配，然后用随机采样一致性算法（random sample and consensus，RANSAC）清除误匹配的点［21］。最后，利用SFM方法进行结构的三维模型重建，形成稀疏点云。

2.2 多视图立体视觉

多视图立体视觉方法是机器视觉中一种常用的数据稠密化处理方法。首先，利用CMVS（clustering views for multi-view stereo）算法将稀疏点云聚类到不同的群集［22］，每个群集的图像数量小于某个阈值，并且各个群集之间有重叠［23］。聚类完成后，利用PMVS（patch-based multi-view stereo）算法重复生成新的面片来稠密化点云。

2.3 泊松表面重建

在得到稠密点云数据后，利用泊松表面重建算法生成三维模型的表面［24］。假定点云模型的表面采样点为均匀分布，通过求解空间泊松方程由有向点集生成表面，最后提取等值面，得到一个由许多三角形拼接成的完全闭合的表面。

2.4 纹理映射

纹理映射是为了生成有颜色和纹理信息的结构三维模型。其具体思路为：首先，建立贴图与三维空间坐标的映射关系；其次，根据相机标定参数，可以得到结构三维模型表面的三角面片的位置以及其在二维图像中的纹理信息，但一个三角面片可以在多幅图像中出现，需要综合考虑。

3 三维建模效果分析

本文首先采用Visual SFM 软件实现稀疏点云的重建［25］；其次，使用CMVS 及PMVS2工具稠密化点云；最后，采用Meshlab软件完成泊松表面重建和纹理映射［26］，并对比了混凝土块的原始图像和压缩后图像及由二者分别恢复重建的混凝土块三维模型。

将K值由小到大分别取为K=2、K=3和K=4，图3为不同K值下压缩后的混凝土块图像及其三维模型，t为三维建模所花费的时间。

图3 不同K值下的混凝土块压缩图像和其三维模型Fig.3 Compressed images of the concrete block and its 3D models under different K values

由图3可知：结构三维模型建模时间随着K值的增大而减少，且当K=2时，时间减少的幅度最大，大约为原图像建模时间的67%。另外由图像可看出：随着K值的增大，重建出的结构三维模型的质量在逐渐下降。

为了保证PCA 算法压缩后的图像在震损结构三维模型快速重建中的实用性和可行性，选择一个抗震性能试验中破坏的装配式密肋空心剪力墙为实验对象，剪力墙的尺寸如图4 所示。图像采用Canon EOS600D相机拍摄，图像分辨率为5 184×3 456，共44张。部分受损剪力墙图像及其三维模型如图5所示，利用PCA算法压缩后的图像及其三维模型如图6所示，此实验中K的取值为2。由剪力墙原始图像重建其三维模型花费时间为2 530 s，由压缩后的图像重建其三维模型花费时间为954 s，重建效率约提高了62%。

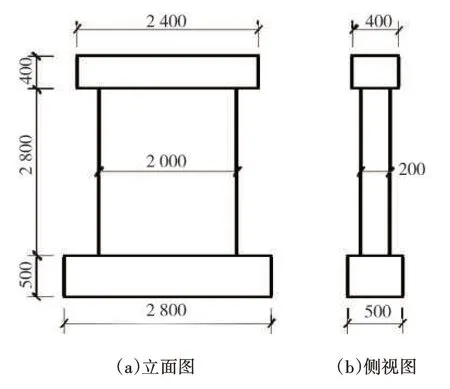
图4 剪力墙尺寸图（单位：mm）Fig.4 Dimension of the shear wall（Unit：mm）

图5 受损剪力墙原始图像和其三维模型Fig.5 Original images of damaged shear wall andits 3Dmodel

图6 受损剪力墙压缩后图像和其三维模型Fig.6 Compressed images of damaged shear wall andits 3D model

对剪力墙实际结构与基于压缩图像重建出的三维模型的部分标定点间（图7 中AB、BC 和FG）的尺寸进行了测量得到了其尺度变换关系，利用该尺度关系对受损剪力墙三维模型进行了尺度变换，其中结构三维模型使用的是结构稠密点云。基于原始图像与压缩后图像分别重建出的结构三维模型尺度变换关系见表1。对结构三维模型尺度变换后，利用剪力墙上剩下的标定点（图7 中DE、HI 和JK）和裂缝宽度对模型的尺寸进行验证，受损剪力墙实际结构与利用尺度关系缩放后的三维模型的尺寸误差见表2。

表1 剪力墙实体结构尺寸与三维模型尺度变换关系Table 1 Dimension of the shearwall and scale factors between the dimension of 3D models and its actual structure

表2 剪力墙三维模型与其实体结构尺寸误差Table 2 Dimensional error between 3D models of the shear wall and its actual structure

图7 剪力墙标定点示意图Fig.7 Schematic diagram of calibration points of the shear wall

由表2可知：基于原始图像重建的受损剪力墙三维模型总体尺寸平均误差为1.22%，而基于PCA 算法压缩后的图像重建出的结构三维模型总体尺寸平均误差为1.78%，对于震损结构快速评估的研究，可以认为误差在允许范围内。

为了验证主成分分析算法对真实结构模型重建的可行性，本文又对一个实际单体建筑进行研究，用于重建的单体建筑图像采用无人机拍摄获得，图像分辨率为5 280×2 970，共110张，其原始图像与利用PCA 算法压缩后部分图像如图8所示，此实验中K的取值为2。

图8 单体建筑原始图像及其压缩后图像Fig.8 Original images and compressed images of the single building

由原始图像和压缩后图像重建出的三维模型如图9 所示，原始图像重建过程花费时间为181 min，同样环境下压缩图像三维重建时间为115 min，重建效率提高了约36%。同样对模型的尺寸误差进行了验证，图9中红色点为标定点，蓝色点为测点，单体建筑的实际尺寸及其三维模型尺度变换关系见表3，三维模型与实际尺寸的误差见表4。

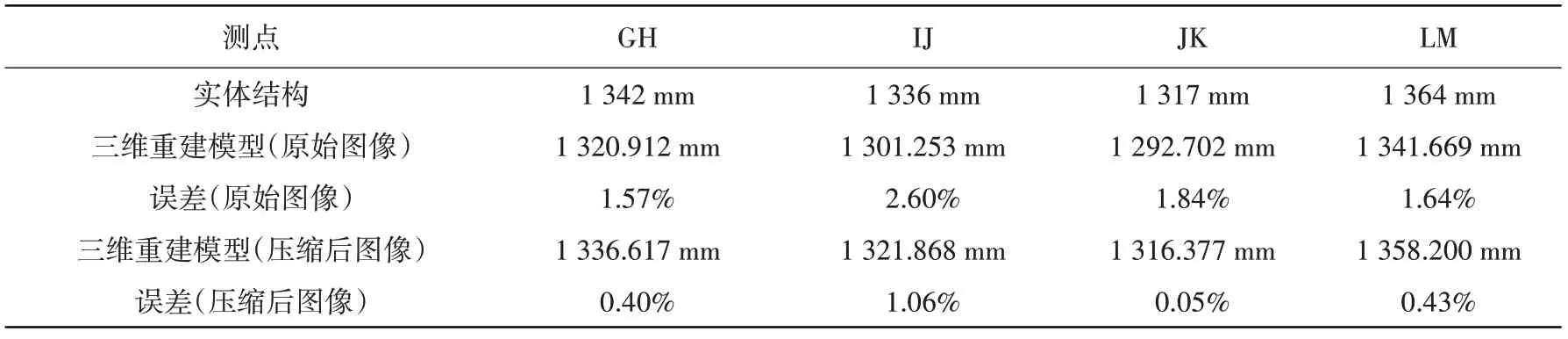
表4 单体建筑三维模型与其实体结构尺寸误差Table 4 Dimensional error between 3D models of the single building and its actual structure

图9 单体建筑三维模型Fig.9 3D models of the single building

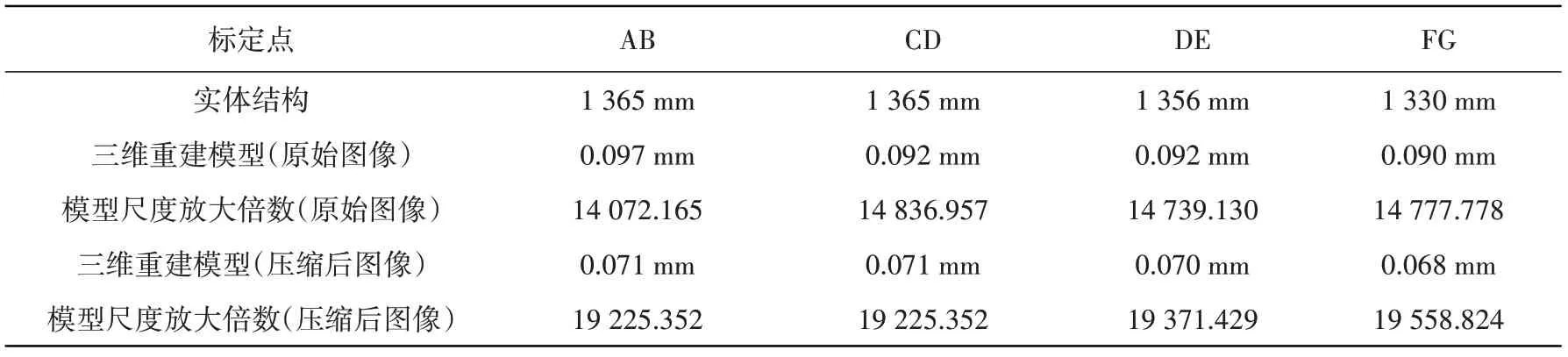
表3 单体建筑实体结构尺寸与三维模型尺度变换关系Table 3 Dimension of the single building and scale factors between the dimension of 3D models and its actual structure

从表4 的结果中可看出：基于原始图像重建的单体建筑三维模型总体尺寸平均误差为1.91%，而基于PCA 算法压缩后的图像重建出的结构三维模型总体尺寸平均误差为0.49%，由此得出本文提出的方法在不影响模型精度的情况下可以显著提高大型结构三维建模的效率。

综合受损剪力墙和单体建筑的实验结果可以得出：本文提出的方法在误差允许范围内相对完整恢复出大型及受损结构的三维模型，且显著提高了建模效率，因此对于大型震损结构的快速评估由PCA 算法压缩后的图像重建出的结构三维模型满足实用性和可行性的要求。然而由压缩后图像重建的三维模型精细程度较由原始图像重建的三维模型有所降低，这是由于图像分辨率的限制，如果图像分辨率越高，重建的三维模型纹理会越清晰。

4 结论

由于建筑结构及构件尺寸较大、建模时间过长，使其在震损结构评估的应用中受到了限制。本文针对上述问题，提出了基于图像压缩方法的三维模型快速重建技术。利用PCA 算法压缩震损结构图像，再基于此进行结构三维模型重建。为了验证本文提出方法的可行性，对一个混凝土块，实际的受损剪力墙以及大型单体建筑进行了三维模型重建，分别对比了三者由原始图像和压缩后图像重建出结构三维模型的建模时间，对比结果表明：在不影响结构三维模型精度的前提下，将图像压缩算法PCA 引入到结构三维模型重建的技术中可以将建模效率至少提高约30%，最多可达约60%。因此本文提出的方法在满足建筑整体震损状况的研究需要下，可极大地减少模型的重建时间。