变长非参数认知诊断自适应测验终止规则

2022-02-18李俊杰郑慧婧康春花

江西师范大学学报（自然科学版） 2022年6期

李俊杰,郑慧婧,康春花*

(1.北京师范大学中国基础教育质量监测协同创新中心,北京 100875;2.浙江师范大学心理学院,浙江金华 321004)

0 引言

认知诊断计算机化自适应测验(cognitive diagnostic computerized adaptive testing,CD-CAT)结合了认知诊断理论和CAT的双重优势,相比传统的测验形式,它可以更精确、更迅速、更灵活地测量出被试的潜在知识状态(knowledge state,KS),从而获得被试在知识点上的掌握情况,为教育教学工作者提供有针对性的指导,促进学生的个性化发展.近年来,国内外越来越多的研究者关注CD-CAT这一领域.

在对CD-CAT的众多分类中,依据CD-CAT使用的诊断方法可将CD-CAT分为参数CD-CAT 和非参数CD-CAT.参数CD-CAT的诊断方法常用极大似然估计法(maximum likelihood estimation,MLE)、极大后验估计法(maximum a posteriori,MAP)和期望后验估计法(expected a posteriori,EAP).这3种方法都是在项目参数已知的条件下通过概率计算来估计被试的知识状态(knowledge states,KS)或属性掌握模式;而非参数CD-CAT是采用更加简单的有效距离判别法来估计被试的知识状态,在估计过程中不需要进行概率计算,进而也不需要知晓项目参数,所依据的是理想反应和观察反应之间的距离最小的原则,即与观察反应之间距离最小的理想反应所对应的属性掌握模式视为考生的知识状态.参数CD-CAT和非参数CD-CAT的结构均包含5个部分:题库、初始项目选择方法、知识状态或能力值的估计、选题策略和终止规则.目前参数CD-CAT已在选题策略[1-6]、属性在线标定[7-9]和终止规则[10-11]等方面展开了相关的研究.相比于参数CD-CAT,非参数CD-CAT发展较晚,截至目前,非参数CD-CAT的研究主要集中在选题策略[12]方面.而大部分围绕选题策略的非参数CD-CAT研究均是以定长(fixed-length)CAT的形式作为终止规则,即固定每次测验的长度,在被试完成测验后,根据被试的作答反应估计其知识状态.定长CAT虽然固定了测验长度,施测较为方便,但对不同的被试会有不同的测量精度.一个更加合理的做法是,应该使CD-CAT形式的测验对每个被试的测量精度相同,这也正是自适应测验优势的体现[13].与定长CAT相对应的终止规则为变长(variable-length)CAT,变长CAT能够使每个被试具有相同测量精度并由此终止测验[14].相对于定长CAT,变长CAT更能体现出自适应的特点和优势,因此,开展这方面的研究非常有意义.总体来讲,传统CAT测验终止规则可以归纳成2类:1)达到预设测验信息量终止规则,即不断施测项目直到测量标准误差落在可接受范围内,或测验信息量达到某个预先设定的指标;2)最小信息量终止规则,即在剩余题库中所有项目的项目信息量都低于某个预设水平[7].在参数CD-CAT中,C.L. Hsu等[10]在C. Tatsuoka[15]以最大后验概率作为测验终止条件的基础上提出了变长CD-CAT的终止规则(本文将其称为Hsu法).其研究结果表明:当固定属性掌握模式在后验概率分布中的最大后验概率预设水平时,被试的模式判准率会随着第2大后验概率预设水平的降低而增大;当固定知识状态后验分布的第2大后验概率预设水平时,被试的模式判准率会随着最大后验概率预设水平的升高而增大.参数CD-CAT的变长测验终止规则的提出极大推动了变长参数CD-CAT发展.正如前文所述, C.L. Hsu等[10]对变长CD-CAT的终止规则是建立在后验概率的基础上的,而在非参数CD-CAT情境中,通常在题库建设过程中标定题目的项目参数,此时HSU法或Tatsuoka法将无法适用于非参数CD-CAT情境.那么,在非参数CD-CAT的体系内有没有类似参数后验概率的指标可用于衡量某个属性掌握是被试真实知识状态的可能性呢?文献[16]率先尝试使用距离加权(dwac)结合理想反应的方式构建了距离加权-理想作答选题方法(DWIR),并阐述了在测验中随着测验长度的增加,更高可能性是被试的属性掌握模式的dwac值越大,更低可能性是被试的属性掌握模式的dwac值越小.

因此,本文首先借鉴变长参数CD-CAT的终止规则,随后结合在文献[16]提出的DWIR方法中距离加权(dwac)的指标开发2种非参数变长CD-CAT的终止规则:最大距离比例终止规则和距离比例双重标准终止规则.

1 认知诊断模型

1.1 DINA 模型

该模型因为仅涉及失误和猜测2个参数,所以真正实现了对认知诊断模型的简化[17-18].其表达式为

其中ηij是一个二分变量,它表示被试i是否掌握了第j题所考查的全部属性,gj表示第j题的猜测参数(guess parameter),其是未掌握该题所测全部属性的被试答对这道题的概率,s表示第j题的失误参数(slip parameter),其是掌握了该题所测全部属性的被试答错这道题的概率.

1.2 RRUM模型

缩减的再参数化统一模型(reducedreparame-terized unified model,RRUM)是另一种常用的认知诊断模型[19-20].RRUM模型的表达式为

1.3 GP-DINA简介

GP-DINA模型[21]是在涂冬波等[22]提出的P-

DINA模型上拓展而来的,GP-DINA的项目反应函数为

ηij=fx(aiq′jmj/(qjq′j)),

其中ηij是被试i在项目j上的理想得分,mj是项目j的满分值,fx(·)是对被试的理想得分进行取整.

P(Xij=t|ai)=P*(Xij=t|ai)-P*(Xij=t+1|ai),

其中P*(Xij=t|ai)表示被试在题目j上得t分及t分以上的概率,t的取值范围为0～mj(mj项目j的满分值),P(Xij=t|ai)为属性掌握模式ai的被试得t分的概率.

2 选题方法

2.1 Q-最优准则

Xu Gongjun等[23]提出的Q-最优准则的依据为:当考察在领域中的所有属性(设共有K个)时一个测试所需的题量至少为K,即给出了使用最小测试长度K是识别所有属性掌握模式的充要条件.特别是为了达到最小测试长度,在测试中的第1项应当只考察1个属性,随后的题目依次添加1个新属性.应用Q-最优准则选择CD-CAT前K个题目的具体过程如下:

1)初始化题库R(0);

2)为被试i从R(0)中随机选题j,使得题目j的q向量qj=e1.通过删除题目j来更新R(0),即R(0)=R(0)-{j};

3)被试作答题目j,并记录反应向量yi;

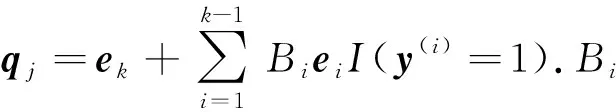
5)对被试施测题目j′,通过y(k)=(yk-1,y(k))更新反应向量;

6)令k=k+1,重复步骤4)～步骤5)直至k=K.

2.2 非参数选题策略(NPS)

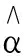
2.3 距离加权-理想作答选题(DWIR)

文献[16]基于理想作答反应构建了非参CD-CAT选题策略,其核心思想是:依据不同属性掌握模式在同一个题目上的理想反应存在差异来选择能够区分被试的估计属性掌握模式与其他属性掌握模式的题目.具体算法如下:

dwac=exp(max{da}-dac)/(exp(max(da)-min(da))),

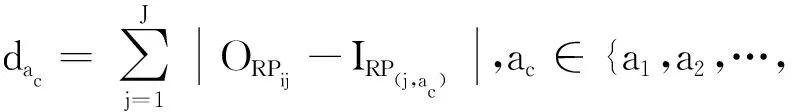
DWIR方法选题过程:1)根据DWIR选题策略,计算题库中剩余题目的DW值,并将在题库中的最大DW值对应的多个题目组成待选题库;2)从待选题库中随机选取一题对被试进行施测;3)重复1)、2)的步骤直至满足测验终止规则.

3 变长测验终止规则

3.1 Tatsuoka法

C. Tatsuoka[15]提出了变长CD-CAT的经验性准则,即当被试属于某种知识状态的后验概率超过设定的标准时,测验终止.

3.2 Hsu法

C.L. Hsu等[10]基于C. Tatsuoka的思想,进一步提出了双重标准的变长CD-CAT终止规则,即当被试在某种知识状态下的最大后验概率P1st不低于某个预设水平(如0.7),并且第2后验概率P2nd不高于某个预设水平(如0.1)时,测验终止.

3.3 最大距离比例终止规则(maximum distance ratio method,MDRM)

在Hsu方法中采用后验概率作为终止测验的精度指标,其原理是若某种属性掌握模式的后验概率越大则这种属性掌握模式就越可能是被试的真实知识状态.已有研究[24-26]表明:与观察反应的距离越小的理想反应所对应的属性掌握模式越可能是被试真正的属性掌握模式.文献[16]采用距离权重的方式用于衡量每个属性掌握模式是被试真实知识状态的可能性,属性掌握模式dwac越大的更有可能是被试的真正属性掌握模式.不难看出,非参数的dwac同样能够作为终止测验的精度指标,同时受C. Tatsuoka[15]启发,本文首先提出最大距离比例终止规则.最大距离比例d1st计算如下:

其中M为潜在的属性掌握模式的种数,m1为在M种潜在的属性掌握模式中dw值最大所对应的属性掌握模式.可以看出,m1的dw值占比越大,d1st的值将会越大.

最大距离比重终止规则:当被试属于某种属性掌握模式的最大距离比例d1st超过设定的标准时,测验终止.

3.4 距离比例双重标准终止规则(distance ratio double standard method,DRDSM)

在文献[15]的基础上,C.L. Hsu等[10]提出了采用双重标准的终止规则以进一步确保测量精度.因此,本文在非参数视角下的最大距离比例d1st基础上进一步结合第2大距离比例d2nd,提出了距离比例双重标准法.

准则1当最大距离比例d1st不小于预定值(如0.70)时,CD-CAT停止.

准则2当最大的非参数比例d1st不小于预定值(如0.70),并且第2大距离比例d2nd也不大于预定值(如0.10)时,CD-CAT停止.

在准则2中考虑d2nd,这可以有效避免2个竞争的属性掌握模式.如假设d1st的预定值设置为0.60,使用准则1,当d1st达到0.60时,CD-CAT停止,此时d2nd可能仍然很高(如接近0.20).若是这样,则会出现2个相互竞争的属性掌握模式,这2个属性掌握模式均有较高的可能性是被试的真实属性掌握模式.解决这个问题的一种方法是将d1st的预定值从0.60增加到0.90,当CD-CAT只有对测验结果非常有信心时,CD-CAT才会停止.有时候,这种程度的自信可能是不必要的.解决这个问题的另一种方法是将d2st设定一个标准,如只有当d1st不小于0.60且d2nd不大于0.20时,CD-CAT才能停止.尽管在理论上可以在第3种或其他d上设置另一种标准,但根据笔者的经验,考虑第1和第2大非参数比例就足够了.

4 在0-1计分情境下的非参数变长终止规则性能

4.1 研究目的

通过模拟研究检验MDRM和DRDSM在0-1计分情境中作为变长终止规则是否具有良好的性能.

4.2 研究设计

该研究采用2选题方法(NPS、DWIR)×4测验终止规则(Tatsuoka、Hsu、MDRM、DRDSM)×3题库质量(HD、LD、HyD)×2属性掌握模式分布(均匀分布、多元正态分布)共48个条件生成数据进行模拟研究,其中选题方法为组内变量,其余变量为组间变量.

终止标准设置:在MDRM和DRDSM中d1st包含2个水平(0.80和0.90);DRDSM的d2nd包含4个水平(1.00、0.20、0.10、0.05).在Tatsuoka和Hsu法中P1st同样包含2个水平(0.80和0.90),Hsu法P2nd包含4个水平(1.00、0.20、0.10、0.05),在计算P1st和P2nd时,采用生成参数真值计算.

在题库方面,研究参照Chang Yuanpei等[12]的研究设计思路,项目库由J=300个项目组成,其中150项目遵守了DINA模型和其他150项目符合RRUM;高质量题库(HD)项目的猜测和滑动均服从均匀分布U(0.10,0.20),低质量题库(LD)项目的猜测和滑动均服从均匀分布U(0.20,0.30),混合质量库(HyD)项目的猜测和滑动均服从均匀分布U(0.05,0.25).在模拟研究中,以0.3的概率考察每个属性生成题目的Q向量.

在模拟被试方面,模拟被试2 000人,分别服从2种属性掌握模式分布.1)被试的属性掌握模式由均匀分布(每个属性掌握模式的概率为1/2K)生成;2)考生的知识状态服从协方差为0.5的多元正态(MVN)分布[27].研究设定最大测验长度为50题,若被试施测50题后仍未达到测验终止的要求,则仍然终止测验.

评价指标采用属性掌握模式判准率:

其中Ri表示被试i的知识状态估计与真值之间一致性,若一致则Ri=1,否则Ri=0,N为测验总人数.PC为考生知识状态估计正确的比例,PC越大表明对被试整体知识状态的估计越精确.

此外还有平均测验长度(mean test length)和测验长度的标准差(standard deviation).

在CD-CAT中采用Q-最优准则进行初始选题,整个研究用R语言自编所有程序进行模拟验证.

4.3 研究结果

表1和表2呈现了在均匀分布下Tatsuoka法、Hsu法、MDRM、DRDSM在0-1计分情境下的表现,由表1和表2可以发现MDRM是当DRDSM的d2nd=1时的特殊情况;Tatsuoka法是当Hsu法的P2nd=1时的特殊情况.整体而言,NPS和DWIR 在使用距离比例作为终止规则时的分类准确性比后验概率终止规则更高,但测验长度更长.可以发现距离比例终止规则与后验概率终止规则类似,测验终止条件越苛刻NPS和DWIR的分类准确性越高,不同的是MDRM和DRDSM分别受到的是d1st和d2nd的影响.在HD题库条件下,d1st取值范围为0.80～0.90,NPS和DWIR的属性分类准确性从0.83增加至0.90,并且在d1st=0.80时,d2nd不同值的PC范围为0.831～0.977,且随着d2nd的减小而增大,在后验概率终止规则下的PC为0.777～0.914.在HyD题库条件下,NPS和DWIR采用MDRM和DRDSM终止测验的PC的结果与HD题库条件的结果相似,这说明在MDRM、DRDSM中距离比例d1st有后验概率P1st相似的作用:在作为测验终止条件时,减小d1st可以提高测验的属性分类准确性.距离比例d2nd与后验概率P2nd有相似的作用:在作为测验终止条件时,减小d2nd可以有效地提高测验的属性分类准确性.在LD题库条件下,NPS和DWIR采用MDRM和DRDSM的属性分类准确性与采用Tatsuoka法和Hsu法的结果相近,特别是当d2nd和P2nd减小到0.05时,NPS和DWIR在不同中终止规则条件下的分类准确性相差小于0.03,这说明:随着测验终止的条件愈发严苛,即d1st和P1st不断接近1或者d2nd和P2nd不断接近0,在采用MDRM和DRDSM作为测验终止规则时取得的结果将与在采用后验概率作为终止规则时取得的结果相同.

表1 在0-1计分和均匀分布条件下的属性分类准确性

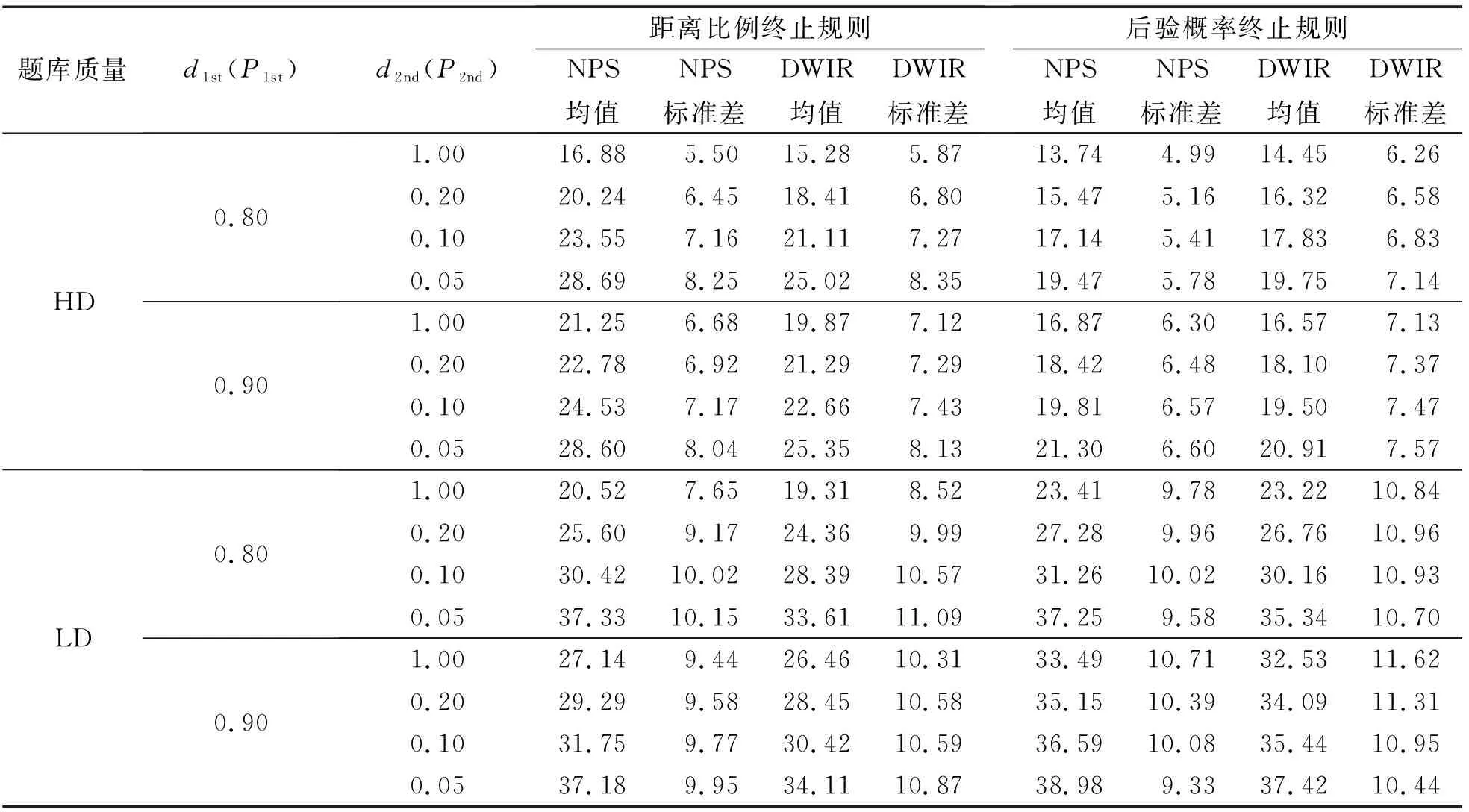
表2 在0-1计分和均匀分布条件下测试长度

表2(续)

在测验长度的使用方面,NPS和DWIR的平均测验长度受到d1st、d2nd、P1st和P2nd的影响.总的来说,NPS和DWIR的测验随着d1st和P1st增大而变长,如在HD题库条件下,d1st从0.80增至0.90,测验长度增加约为2;P1st从0.80增至0.90,测验长度增加约为3.NPS和DWIR的测验随着d2nd和P2nd减小而变长,如在HD题库条件下,d2nd从1.00减至0.05,测验长度增加约为12;P2nd从1.00减至0.05,测验长度增加约为6.观察表2可以发现:在HyD题库条件下的结果与在HD题库条件的结果基本相似.在表2中,LD题库的NPS和DWIR采用MDRM和DRDSM的测验长度与采用Tatsuoka法和Hsu法的测验长度相近,特别是当d2nd和P2nd的减小到0.05时,NPS和DWIR在不同中终止规则条件下的平均测验长度相差小于3.在多元正态分布下的分类结果和题库使用情况与在均匀分布下的均相同,这里不再呈现.

5 在混合计分情境下的非参数变长终止规则性能

5.1 研究目的

通过模拟研究检验MDRM和DRDSM在混合计分情境中作为变长终止规则是否具有良好的性能.

5.2 研究设计

在研究采用2选题方法(NPS、DWIR)×4测验终止规则(Tatsuoka、Hsu、MDRM、DRDSM)×3题库质量(HD、LD、HyD)×2属性掌握模式分布(均匀分布、多元正态分布)共48个条件生成数据进行模拟研究,其中选题方法为组内变量,其余变量为组间变量.整个研究除题库设置方面与上述研究不同,其他条件相同.

在题库方面,题目数量为300,题目的最高分为3分.在高质量题库中题目的猜测参数和失误参数均服从均匀分布U(0.10,0.20),且为随机生成;在低质量题库中题目参数服从均匀分布U(0.20,0.30),且为随机生成,混合质量库(HyD)项目的猜测和滑动均服从均匀分布U(0.05, 0.25).题目sj和gj分布根据文献[21]的设定,sj单调递增,gj单调递减,将随机生成3个sj按升序排列,3个gj按降序排列;在仿真研究中,属性的层级关系为独立性,在题库中的题目平均分布到每种测量模式上(在5个属性时,题库有31种测量模式).

在CD-CAT中采用Q-最优准则进行初始选题,整个研究R用语言自编所有程序进行模拟验证.

5.3 研究结果

表3和表4呈现了在均匀分布下Tatsuoka法、Hsu法、MDRM、DRDSM在混合计分情境下的表现.整体而言,NPS和DWIR的研究结果与在0-1计分情境下的类似,在使用距离比例作为终止规则时的分类准确性比在后验概率终止规则时的更高,但测验长度更长.无论是距离比例终止规则还是后验概率终止规则,均有:测验终止条件越苛刻,NPS和DWIR的平均测验长度越大,属性分类准确性越高;不同的是MDRM和DRDSM分别受到的是d1st和d2nd的影响.同时,从不同题库条件的结果中发现:随着测验终止的条件愈发严苛,即d1st和P1st不断增大或者d2nd和P2nd不断减小,NPS和DWIR在Tatsuoka法和MDRM测验终止规则条件下的属性分类准确率不断接近;Hsu法的结果和DRDSM终止条件下的结果不断接近.此外,在多元正态分布下的分类结果和题库使用情况与在均匀分布下的均相同,这里不再呈现.

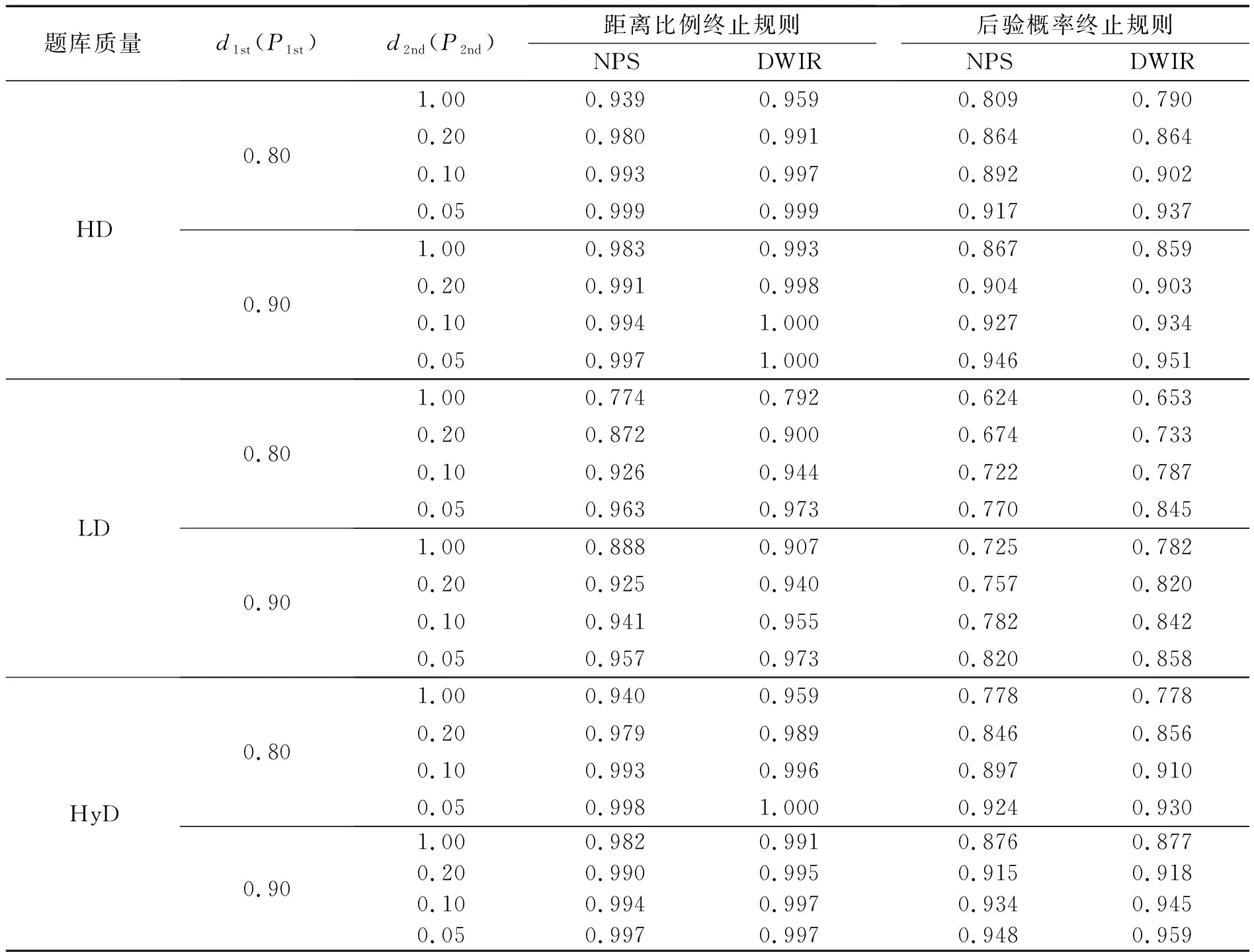
表3 在混合计分和均匀分布条件下的属性分类准确性

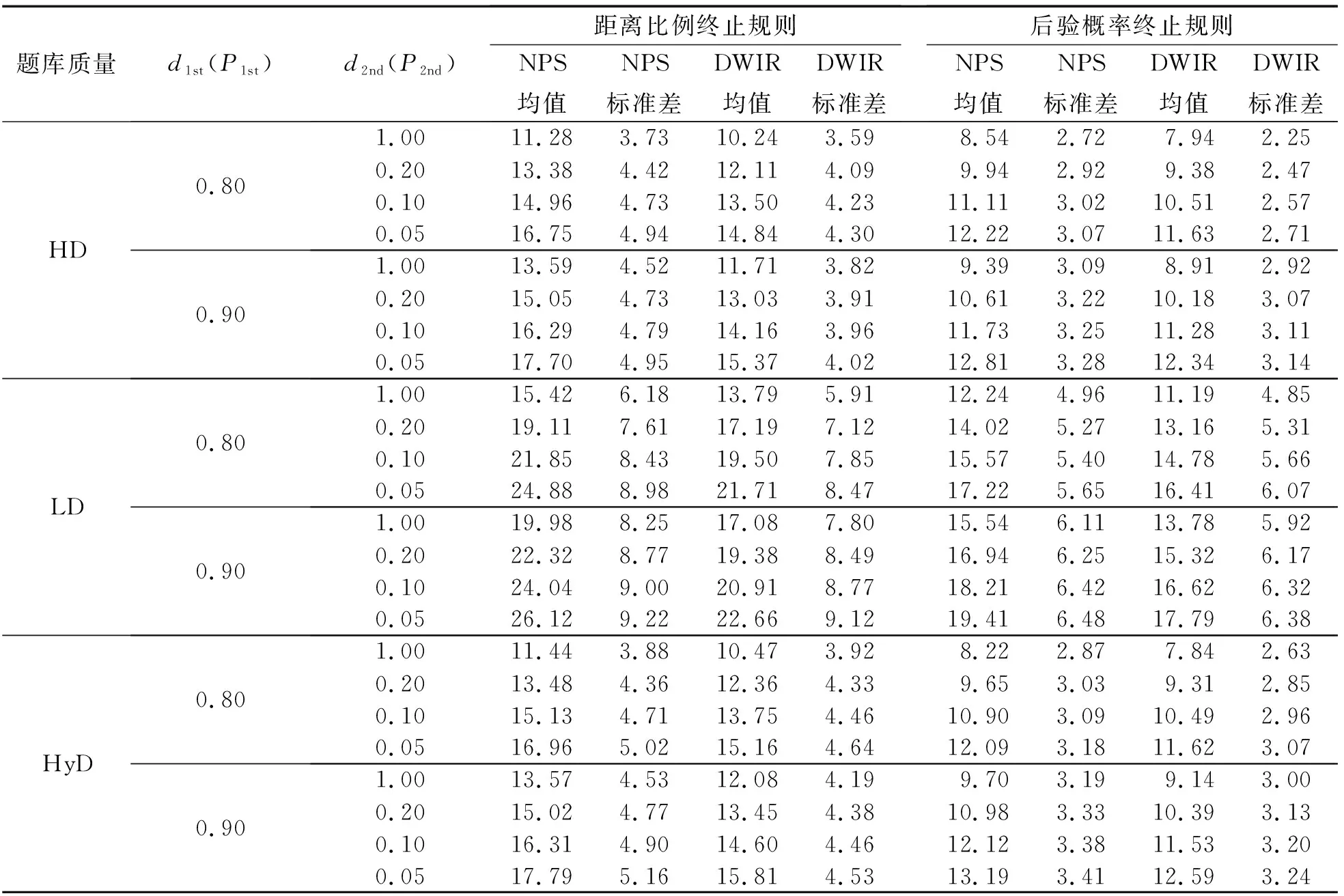
表4 在混合计分和均匀分布条件下测试长度

6 讨论与结论

6.1 研究讨论

目前大部分非参数CD-CAT的研究集中于定长终止条件,虽然定长CAT由于固定了测验长度,所以施测较为方便,但是其对不同的被试会有不同的测量精度.一个更加合理的做法是, 应该使CD-CAT形式的测验对每个被试的测量精度相同,这也正是自适应测验的优势所在.为了发展变长非参数CD-CAT,本研究尝试结合在DWIR方法中的距离权重构建了2种非参数距离比例终止规则MDRM、DRDSM,随后通过模拟研究将采用后验概率终止规则的Tatsuoka法、Hsu法作为MDRM、DRDSM使用效果参照对象来验证MDRM、DRDSM的性能.

2个模拟研究的结果均显示:本文提出的2种非参数距离比例终止规则MDRM、DRDSM获得的分类准确率比采用后验概率终止规则的Tatsuoka法和Hsu法的分类准确率更高,但其代价则是需要更多的测验题目.特别是在0-1计分的情境下MDRM、DRDSM规则所需的题目数量更多,这也可能与0-1计分的计分规则所提供的的信息更少有关,此外,这也可能与研究的MDRM、DRDSM中的距离比例计算有关.在MDRM、DRDSM规则下,虽然设置非参数距离比例d1st、d2nd与后验概率P1st、P2nd相等,但是MDRM、DRDSM达到终止测验的条件d1st、d2nd更加严苛,从而其需要更多的测验题目,进而导致更高的分类准确率.这是在CAT情境中一直面临的利益权衡问题[6-7,11,28].事实上,在MDRM和DRDSM规则下分类准确率的高低与测验长度情况之间的利益权衡可通过研究设置给予实现,当研究目的在于尽可能获得更准确分类结果时,可增加在MDRM 规则下的d1st值,或者在DRDSM规则下增大d1st值和减小d2nd;反之,可以适当减少d1st值或者增大d2nd.最后研究也发现:随着测验终止的条件愈发严苛,即d1st和P1st不断接近1或者d2nd和P2nd不断接近0,在采用MDRM和DRDSM作为测验终止规则时的结果和在采用后验概率作为终止规则时的结果逐渐接近.