不连续多目标博弈的逼近定理
2022-02-18牟玉霜贾文生
牟玉霜,贾文生
(贵州大学数学与统计学院,贵州 贵阳 550025)
0 引言
J.F. Nash[1-2]提出了在博弈论中重要的解概念——Nash均衡,并利用Kakutani不动点定理和Brouwer不动点定理证明了均衡点的存在性.之后一些学者也给出了Nash均衡的存在性定理,这些存在性定理大多数要求支付函数是连续的.然而,在一些重要的经济模型中,支付函数往往是不连续的,于是许多学者将连续性条件减弱,引入伪连续、转移连续、拟弱转移连续等各种不连续的条件,并得到了Nash均衡的存在性结果[3-5].由于博弈问题的解一般来说不是唯一的,所以均衡点的稳定性研究便成为了博弈论的重要课题之一.文献[6]证明了:当支付发生扰动时,若由支付函数定义的Ky Fan 函数是广义正拟转移连续的,则该博弈存在本质的Nash均衡.文献[7]研究了当支付和策略都扰动时满足广义支付条件且支付函数之和上半连续的博弈的通有稳定性.2019年,V. Scalzo[8]引入了一种不连续条件——广义单偏离性,并证明了具有广义单偏离性的n人非合作博弈存在Nash均衡;进一步地,V. Scalzo将广义单偏离性加强为正广义单偏离性,给出了具有正广义单偏离性的博弈Nash均衡的存在性和通有稳定性结果.
一方面,在实际问题中,局中人的支付函数一般是多目标的,因此,多目标博弈更加符合应用问题的背景.1959年,L.S. Shaply等[9]引入了多目标博弈均衡点的概念.Yang Hui等[10]证明了支付函数是连续的多目标博弈弱Pareto-Nash均衡及其本质连通区的存在性.Jia Wensheng等[11]给出了在具有连续支付函数的广义多目标多主从博弈中弱Pareto-Nash均衡的存在性和通有稳定性结果.文献[12]得到了具有模糊约束映射的广义多目标博弈均衡点的通有稳定性及其本质连通区的存在性结果.文献[13]对在伪连续条件下广义多目标博弈弱Pareto-Nash均衡及其本质连通区的存在性进行了研究.
另一方面,在完全理性下,每个局中人在决策时都能选择对自己最有利的策略,这种假设过于理想化,在实际应用中具有一定的局限性.1955年,H.A. Simon[14]提出了有限理性理论,他认为有3个因素会影响人们的决策结果:首先,决策者可以选择近似的策略;其次,每个决策者可以选择近似的函数作为目标函数;最后,在具体的计算中,求解方法也是近似的.因此,人们达到的是在有限理性下的“满意解”,而不是在完全理性下的“最优解”.2001年,L. Anderlini等[15]建立了带有抽象理性函数的有限理性模型,但是该模型的假设条件太强,在很多重要的博弈模型中都无法满足.Yu Chao等[16]将L. Anderlini等[15]的假设条件减弱,并将改进后的有限理性模型应用到均衡点的稳定性研究中.
逼近定理是许多问题稳定性和求解算法研究的重要内容,也是大多数算法的理论基础.俞建[17]给出了在伪连续条件下n人非合作博弈问题和多目标最优化问题的逼近定理.文献[18]证明了在伪连续下均衡问题的逼近定理.文献[19]和文献[20]分别得到了在连续条件下变分不等式问题和群体博弈问题的逼近定理.文献[21]对向量均衡问题的逼近定理进行了研究.目前,有关不连续博弈的研究大多数聚焦于均衡点的存在性和通有稳定性,对于不连续多目标博弈问题逼近定理的研究相对较少.受到以上工作的启发,本文从逼近的角度在有限理性下研究近似弱Pareto-Nash均衡能否收敛于一类不连续多目标博弈精确解的问题.
1 预备知识
首先介绍多目标博弈模型.
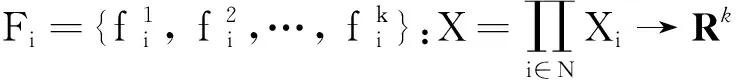

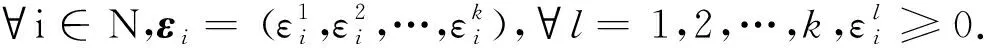
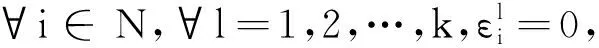
定义2[23]设X和Y是2个拓扑空间,K:X→P0(Y)是一个集值映射,其中P0(Y)表示Y的所有非空子集的集合.
1)若对Y中任意的开集V,K(x)⊂V,存在x的开邻域Ox,使得∀x′∈Ox,有K(x′)⊂V,则称K关于x是上半连续的;
2)若对Y中任意的开集V,V∩K(x)≠∅,存在x的开邻域Ox,使得∀x′∈Ox,有V∩K(x′)≠∅,则称K关于x是下半连续的;
3)若K关于x既是上半连续的,又是下半连续的,则称K关于x是连续的.
V. Scalzo[8]引入了正广义单偏离性的概念,将其推广到向量值函数的情形.
定义3多目标博弈Ω满足向量值的正广义单偏离性,若x∈X不是Ω的均衡点,∃y∈X,j∈N和A={(a,a,…,a)∈Rk:a≥0},有
Fj(yj,x-j)-Fj(x)∈intA,
存在x的一个开邻域Ux和具有非空凸紧值的上半连续映射ζx:Ux→P0(X),使得∀x′∈Ux和y′∈ζx(x′),∃i∈N,有
Fi(y′i,x′-i)-Fi(x′)∈intA.
注21)Fi(y′i,x′-i)-Fi(x′)∈intA表示∀l=1,2,…,k,fli(y′i,x′-i)-fli(x′)>a(a>0).注意到当k=1时,定义3即为文献[8]中的定义4.
2)向量值的正广义单偏离性表示当x不是均衡点时,存在局中人i可以选择由一个具有非空凸紧值的上半连续映射决定的策略y′,即使其他局中人选择轻微偏离x的策略,y′在一个局部保障水平上也能对所有的目标函数产生严格更优的回报.
引理1[17]设{Tn}是在度量空间X中的一列非空有界子集,T是在X中的非空有界子集,O是在X中的开集.若O∩T≠∅且h(Tn,T)→0(n→∞),其中h是在X上的Hausdorff距离,则存在正整数M,使得∀n≥M,O∩Tn≠∅.
引理2[17]设{Tn}是在度量空间X中的一列非空有界子集,T是在X中的紧子集.若h(Tn,T)→0(n→∞),xn∈Tn,则存在{xn}的子序列{xnr},使得xnr→x∈T.
2 不连续多目标博弈的逼近定理
定理1设(Xi,di)是一个度量空间,假设下列条件成立:
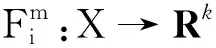
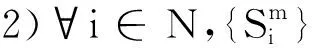

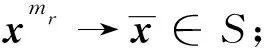

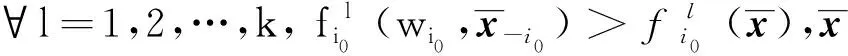

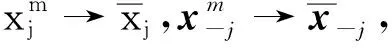
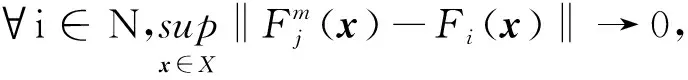
即∀m≥M2,∀l=1,2,…,k,有

这与条件3)矛盾.
注31)若k=1,则定理1为满足正广义单偏离性的n人非合作博弈问题的逼近定理;
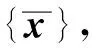
若在定理1中xm∈Sm,m=1,2,…,则结论仍然成立.
推论1设(Xi,di)是一个度量空间,假设下列条件成立:
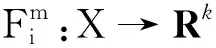
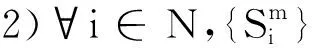
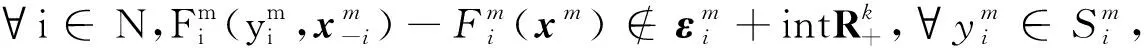
则
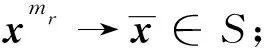
若在定理1中Sm=S,m=1,2,…,则结论仍然成立.
推论2设(Xi,di)是一个度量空间,假设下列条件成立:
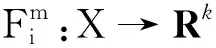

则
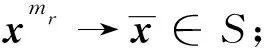

3 结论
本文在有限理性下对满足一类不连续条件的多目标博弈问题的逼近定理进行了研究.运用集值分析的方法,在一定条件下证明了对于一类不连续多目标博弈的弱Pareto-Nash均衡可以用在有限理性下的近似解来逼近在完全理性下的精确解.为有关不连续多目标博弈问题的稳定性和求解算法提供了理论支撑,并显示了可以用有限理性逼近完全理性.
