形式无约束下偏好集映射、拓扑交和一致性

卢美华,高晓波

(1.江西科技学院理科部,江西 南昌 330022;2.江西农业大学计算机与信息工程学院,江西 南昌 330045)

0 引言

中国拓扑学自身发展尤有特点，甚至可以说，拓扑学在中国的发展达到了一种自为的状态[1].拓扑在技术特征上粗糙性和可精细性能够灵活协调，从而在社会科学理论构造中具有十分突出的作用[2].序拓扑的发展已经具有体系化成果[3].事实上，正是由于交叉发展的需要,所以序拓扑受到了多个国家自然科学基金项目的支持[4].序拓扑空间能超越一般度量并更适用于弱性空间，序拓扑空间在选择理论中的基础性地位也更为突出.序方法在决策理论甚至物理社会理论、结构社会理论中都有广泛的应用.当然，在决策理论中的一些基本概念正是运用序方法才得以开拓.如理性是决策理论的基础，运用序方法给出了有限理性的构造方式[5].

另外，在结构上的序拓扑性质显然独立于其刻画方式.但是，序的结构性拓扑加载却因序刻画方式的不同而产生不同的便利性，因此序刻画方式在决策理论约束公理的配置中甚为重要.文献[6]表明:群决策共识和一致性的研究同样在系列国家自然科学基金的资助下获得了深度研究，但一致性公理化有待于进一步推进.然而,若引入集值映射来刻画序，则一致性可表现为某种无条件运算，序的集映射刻画的便利性十分明显，后续约束公理的加载更灵活广阔.当然，由于序拓扑的性质在结构上显然独立于刻画方式，所以其共识、一致性未必存在，这将在运算上有所表现，即表现为全局交空、定点交空，进而一致性(共识运算)失效.即使这样，交运算为形式刻画一致性构造了一个普适性框架，这将给出一致性研究的一种新路径.当然，一致性是美国国家工程院院士T.L. Saaty[7]于1994年从权重比例的相容性提出的；该“一致性”概念、一致性度量在层次分析法和统计决策中应用最为广泛，但最初的目的是从群决策方向上解决社会选择的Arrow不可能问题[7].从而，融合序拓扑和决策具有重要的理论和实践意义.

本文采用集映射来刻画偏好序，基于标度空间考察标度偏好序的共识运算、一致性运算的拓扑交形式刻画；拓扑交是一种无条件运算，从而能形成在基底层面上的结论.在序理论的广阔体系上，本文聚焦于偏好序构造的基本体系，即共识运算存在性、偏好序完全性、严格性拓扑交特征、偏好序分解的拓扑交，并获得了基本结论，为序拓扑理论及其构造性应用在基底层面上形成了逻辑支撑.同时，严格采用拓扑交以体系化编撰偏好序的重要方法，将为偏好序的“一致性研究”后续拓扑加载提供广阔的空间.当然，本文所言及的共识和一致性是同一个概念，仅仅是要因袭不同文献而同时采用.

1 基本概念和集序框架

设(X,≼)中“≼”关系满足传递性，称“≼”为偏序；一般地，当(X,≼)中传递性关系“≼”还满足自反性时,可记F:X→2X为择优映射，其中F(x)={y|x≼y}.另外，传递自反性偏序集(X,≼)可以分解，在(X,≼)中记“x～y⟺x≼y且y≼x”，记“xy⟺x≼y且y≼x”.显然(X,)也是偏序集，是(X,≼)严格化，由此可导出严格择优.当偏序集(X,)中偏序满足传递性、非自反性时，称之为严格偏序.记为称之为严格择优映射，也称之为F导出的严格择优映射.另外，可定义“≼”≡“≻”,“”≡“≻∪～”等,其含义是能自明的.再者，在仅仅满足传递性的偏好集(X,≼)中，偏好关系不是完全的；但一些完全性偏好集(X,≼)集结后会部分丧失“≼”的完全性，不过依然保持上界关系，这就是偏好格.

虽然后续“一致性”概念以数值测算广泛应用于量化决策理论和实践之中，但T.L. Saaty最初却是通过“解决其群体基础偏好的相容性和一致性”来解决Arrow不可能性问题.徐玖平等[6]系列研究提出了各种复杂偏好信息的表征与处理策略,并且在一定程度上突破了共识(一致性)成本和共识(一致性)决策行为过程难以刻画的瓶颈,吴志彬[8]从多种结构提出了“共识(一致性)”测度.但是，这些研究特别是文献[8]的各种结构下“共识(一致性)”需要纳入统一框架，并且这本身也在寻求某种共识(一致性).显然,从无条件运算上构造界定“一致性”的框架将具有最广泛的容纳性.

为此，通过集映射刻画偏好序并用集值交运算刻画一致性、共识就十分便利,这是一个新框架，不妨称之为集序框架.当然，集映射刻画偏好序和集值交未必能达到数值测算一致性，但若增加拓扑结构则可以达到.另外，无论是在何种映射空间上定义度量，或者加载拓扑，虽然可以测算“映射对”之间的差异，但均无法测算“映射族”上的差异，而集映射刻画偏好序和集值交在强拓扑结构下测算“映射族差异性”却十分便利.因此，集映射序和集值交在共识测度上比在度量测度上更具适应性.

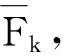
定义1对于备择物集A={α1,α2,…,αi}、标度集V={1,2,…,j}及每个k∈V,称集值映射Fk:A→2A为择优映射，若∀α∈A,则α∈Fk(α),且α0∈Fk(α),于是Fk(α0)⊂Fk(α).同时，称H={F|F:A→2A为择优映射}为择优映射空间，被简称为择优空间.对k∈V,Hk为择优空间，则称HV=H1×H2×…×Hj为V标度择优空间.称S:HV→H为共识映射,S(F1,F2,…,Fj)=FV,其中FV:A→2A为FV(α)=∩k∈VFk(α).

显然，共识映射是一种社会选择函数，若FV:A→2A刻画了某个偏好，则共识映射就集结了偏好.更一般地，共识映射结合约束公理还解决了从个体偏好到群体偏好的可集结问题.当然，FV:A→2A是非空的;不过，共识映射未受任何规范约束；再者，在集序上也可以加载约束公理，在强约束公理下，如何保障FV:A→2A的非空性是公理配置机制的核心，也是协调规则的关键之处.为后续方便，记集序框架为(A,V,H,HV,S).

2 主要结果

在集值映射刻画偏好中和在以共识映射确定标度集序的共识中，并没有施加规范约束公理，共识运算也是粗糙的，甚至不能保证共识存在.当然，无论是按照社会选择理论加载规范约束公理，还是按文献[6]测算共识，集序框架都是普适的，且共识存在也均是弱性条件的.另外，通过共识运算及其强弱化过程可以刻画框架(A,V,H,HV,S)的整体特征.

2.1 共识运算存在性

定理1在(A,V,H,HV,S)中,共识运算S存在且是非空的.若S(F1,F2,…,Fj)恰为恒等映射,则S(F1,F2,…,Fj)(α)⊂∩F∈HF(α),即共识运算是冗余的.

证在(A,V,H,HV,S)中,A={α1,α2,…,αi},V={1,2,…,j}.对每一k∈V,k在A中装载偏好序为Fk:A→2A,其必然满足∀α∈A有α∈Fk(α).共识映射S:HV→H为S(F1,F2,…,Fj)=FV,其中FV(α)=∩k∈VFk(α),那么，∀k∈V,α∈Fk(α),显然有α∈∩k∈VFk(α)，即α∈FV(α).从而∀α∈A有α∈FV(α),这保证了共识映射在S(F1,F2,…,Fj)=FV中的非空性.从而，要证S存在且非空，即证明FV∈H.

为证明FV∈H,任取α0∈FV(α),则α0∈

∩k∈VFk(α).从而对于每个k∈V,α0∈Fk(α),且Fk∈Hk,按照择优映射空间Hk定义，必有Fk(α0)⊂Fk(α).因此对于V必有∩k∈VFk(α0)⊂∩k∈VFk(α).由S(F1,F2,…,Fj)=FV确定FV(α)=∩k∈VFk(α),也就是FV(α0)=∩k∈VFk(α0)⊂∩k∈VFk(α)=FV(α).

综上可知,∀α∈A有α∈FV(α),且α0∈FV(α),则FV(α0)⊂FV(α),即证明了FV∈H.于是，本定理余下部分只需证明当S(F1,F2,…,Fj)为恒等映射时运算的冗余性，冗余性除去单点分解性外就是S(F1,F2,…,Fj)(α)⊂∩F∈HF(α).显然,当S(F1,F2,…,Fj)=FV为恒等映射时，∀α∈A均有FV(α)={α}.而∀F∈H,按择优映射空间H定义，∀α∈A均有α∈F(α),从而α∈∩F∈HF(α),FV(α)={α}⊂∩F∈HF(α),即证明了当S(F1,F2,…,Fj)为恒等映射时共识运算的冗余性.

定理1得证.

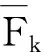
另外，若序集(X,≼)满足完全性、传递性、自反性，则其F:X→2X为择优映射必满足∀αk、αt∈A,必有αk∉F(αt)⟺αt∈F(αk).若在HV中每个标度偏好序Fk都是完全的，则在每个{α1,α2,…,αi}经过适当重排为{β1,β2,…,βi}后，可保证标度k有Fk(β1)⊂Fk(β2)⊂…⊂Fk(βi),但FV(β1)、FV(β2)、…、FV(βi)却未必有包含链.不过，严格序在交运算后仍然可以判断当任何2个F(αt)与F(αk)交不空时要么为包含关系(即F(αt)⊂F(αk)或F(αt)⊃F(αk)),要么集合相等关系F(αt)=F(αk).为此，定义H′={F′|F′:A→2A为完全偏好序的择优映射}.显然，H′⊂H为一般择优空间的子集，称H′为全序择优空间.对于k∈V，若H′k为全序择优空间，则称H′V=H′1×H′2×…×H′j为V标度全序择优空间.但是，把共识映射限制在V标度全序择优空间H′V上，其映像未必是在全序择优空间H′中，从而在H′V上的共识运算未必是内射的，故仍然为S:H′V→H.V标度全序择优空间的框架为(A,V,H,H′V,S),并且在此框架中H′仍保留着偏好序的自反性，从而有如下推论成立.

推论1当V标度全序择优空间的框架为(A,V,H,H′V,S)时,共识运算S存在且是非空的.

2.2 完全性、严格择优特征

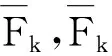
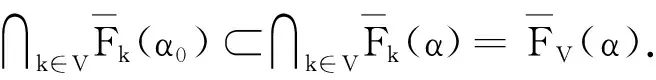
Inclusion criteria and exclusion criteria of literature for data mining were evaluated according to the following items.

注2定理2的证明过程是基于共识运算S具有非空交的条件，这一条件在无限连续备择物集条件下是平凡的,但有限离散备择物集的S却未必能无条件地存在非空交.按文献[11]考察的IIA公理，局部共识运算能存在非空交，从而整体共识运算能存在非空交，但在IIA公理中从局部到整体的机制还未厘清.关于无限连续备择物构造，考虑齐齐尼尔斯基的连续性备择物空间即可，胡卫群[12]确实也肯定了连续性备择物空间的现实性.而戈登·塔洛克[13]在美国军费预算方案表决局势的研究中已经提炼了无限连续备择物的实例.

注3定理2表明:若交运算在严格偏好序集上或者在完全偏好序集上构造逐点构造共识，则在集结方向上必然有格序偏好，这说明标度偏好的一些特征并不能在集结中得到保持.在完全性、严格偏好序的集结中，标度集V的调整、划分形成标度分类说明分类性的交运算具有更好的一致性，文献[14]中的格序上、下界的运算能通过“分类一致性”指导化解这里的集结一致性.

2.3 分解构造特征

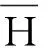
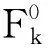
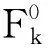
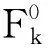
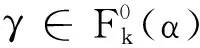
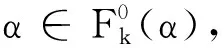
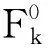
推论2即为文献[9]中的重要定理，这也说明拓扑交的适用广度.

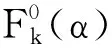
注5这里等价性通过交运算来构造；备择物集能通过任何2个择优映射做交运算能形成“最小非空映像集交”.本文全部是用基本的交运算形成构造性分析，虽然通过分解形成“≼”≡“≻”,“”≡“≻∪～”等关系对相关定理进行证明更为简便，但是，在形式公理化体系下相关结论要依据基本公理形成定理方式予以体系化编撰.而本文所有概念、判断、定理都落到交运算上予以刻画，能形成更为严密的公理编撰体系.

3 讨论

文献[6]指出:在国家自然科学基金的资助下，群决策共识和一致性的研究同样在系列国家自然科学基金中获得了深度研究，但一致性、共识的公理化刻画有待于进一步推进.不过，若引入集值映射来刻画序，则一致性可表现为一种无条件运算，序的集映射刻画的优势就十分明显，后续约束公理的加载是广阔的.同时，若回到基本的拓扑交运算予以构造共识、一致性等概念，则在公理系统的系统编撰中结构化逻辑是严格的和层次化的.当然，采用拓扑交形成的编撰体系逻辑严格，层次清晰；事实上，拓扑交是一种无条件运算，本文诸结论基本涵盖了偏好序构造的基本体系，为序拓扑理论及其构造性应用在基底层面上形成了逻辑支撑，但也存在些许缺陷，即全局交空、定点交空，一致性(共识)在运算层面上失效[15].