聚乙烯流化床反应器气-液-固流场中升力模型的影响研究
2022-02-18李永帅郑毅李岚李新爽赵馨怡潘慧凌昊
李永帅,郑毅,李岚,李新爽,赵馨怡,潘慧,2,凌昊
(1 华东理工大学化工学院,上海 200237; 2 上海电力大学环境与化学工程学院,上海 200090)
引 言
聚乙烯具有化学性质稳定、耐低温性强、电学性能优异、加工性能好等优点,是当今主要的热塑性树脂材料,应用范围广泛[1]。气相法[2-3]是生产聚乙烯的主要工艺,但是该工艺存在一定的能量消耗,反应过程中移热能力有限,冷凝技术可以很好改善这一现象。冷凝技术[4-5]是将惰性液体随气相加入到反应器中,液相迅速蒸发吸收大量反应热,同时并不影响流化床的稳定性,提升了时空产率,受到了学者们的广泛关注。例如,阳永荣课题组[6-10]深入研究了冷凝模式下反应体系热性能、固相颗粒过热、床层温度分布、反应器稳定性及动态行为等内容。目前,一般假设液相在FBR(fluidized bed reactor)进料入口处便迅速蒸发,反应器内部为气固两相流,这一假设与实际工业情况存在一定差异。Pan 等[11]提出了液相蒸发模型组并与CFD(computational fluid dynamics)模型耦合,研究了液相在FBR 内部蒸发对于流体流动和行为的影响,模拟结果表明,液相蒸发会使流化床内的流体流型由羽流流型转化为旋转流型。升力是颗粒周围不对称流动和/或颗粒本身旋转而形成垂直于其相对运动方向的横向力[12-13],因此流体变为旋转流型使升力对于多相流的动力学行为和相分布特性的影响不可忽略。
相间力一般包括曳力、升力、壁面润滑力、虚拟质量力和Basset 力。相间力构建了相间的力学平衡,确定了沿流动通道的相分布模式,在多相流建模中起着至关重要的作用。毛在砂[14]介绍了曳力、升力、虚拟质量力和Basset 力的数学模型和应用范围,建议一般情况下虚拟质量力和Basset 力较小可以不用考虑。Wang 等[15]更为深入地探究了流体在三个Reynolds 数条件下不同曳力、升力和壁面润滑力模型造成的影响和差异,计算结果确定了在不同Reynolds 数下各相间力的最优化模型。Yao 等[16]通过模拟验证了Syamlal-O’Brien 和Gidaspow 等4 个曳力模型对于多分散聚合FBRs 的气固相流动有显著影响,研究中忽略了升力模型的影响。Hibiki等[17]详细总结了升力模型的现状、升力系数模型的发展,对单粒子系统和多粒子系统的升力进行了讨论,总结了不同升力模型适用的条件和范围,提供了丰富的理论依据。Zhang 等[18]应用CFD-PBM(population balance model)研究了相间力对气泡柱的模拟影响,结果表明升力对径向气体滞留量、局部气体滞留量、轴向液速、整体气泡尺寸分布和整体Sauter 平均直径均有显著影响,考虑升力可以明显提高模拟结果的精度。目前,国内外学者对于相间力的研究主要集中在两相流体系中,关于升力的研究也多局限于管道流动或小型反应器中[18-22],尚未有关于三相流聚乙烯FBR中升力模型的研究。
在持液聚乙烯流化床反应器中,液体引入后,在反应放热的影响下,液相蒸发,从而对流化床中的流体结构产生影响,使流体流型由羽流流型转化为旋转流型,而升力是颗粒周围不对称流动和/或颗粒本身旋转而形成垂直于其相对运动方向的横向力,因此流体变为旋转流型使升力对于持液的聚乙烯反应器的流体流动行为和相分布特性的影响不可忽略。因此,本文以冷凝模式下液体引入的聚乙烯流化床反应器为研究对象,提出了一个耦合颗粒动力学理论、液相蒸发,聚合反应和相间传热的三相欧拉流体CFD 模型来描述反应器中气-液-固三相流流体流动。同时,在三相CFD 耦合模型中,气-固相间的升力分别采用三种不同经典的升力模型:Saffman-Mei 模 型、Legendre-Magnaudet 模 型 和Moraga 模型,以此探究升力模型对反应器中气-液-固三相流场流动行为的影响,为持液聚乙烯流化床反应器的设计与优化提供指导。
1 数学模型
1.1 欧拉三流体模型
根据模拟所设置的反应器尺寸以及由于冷凝模式下反应器内部的三相流体系的复杂性,研究中采用的是CFD 欧拉三相流体模型,气、液、固三相均被看成相互渗透的连续性流体。
连续性方程:

动量方程中的气液相间、气固相间、固液相间采用不同的曳力模型计算,气、固相动量方程中的Flift为升力,液相在反应器内含量较低,为了更加明确地对比升力模型的影响,暂不考虑气液相、液固相之间的升力影响。
气液相之间的曳力模型为Schiller and Naumann 模型[23],气固相之间的曳力模型为Gidaspow 模型[24],液固相之间的曳力模型为Morsi and Alexander 模型[25]。
能量方程:
气相
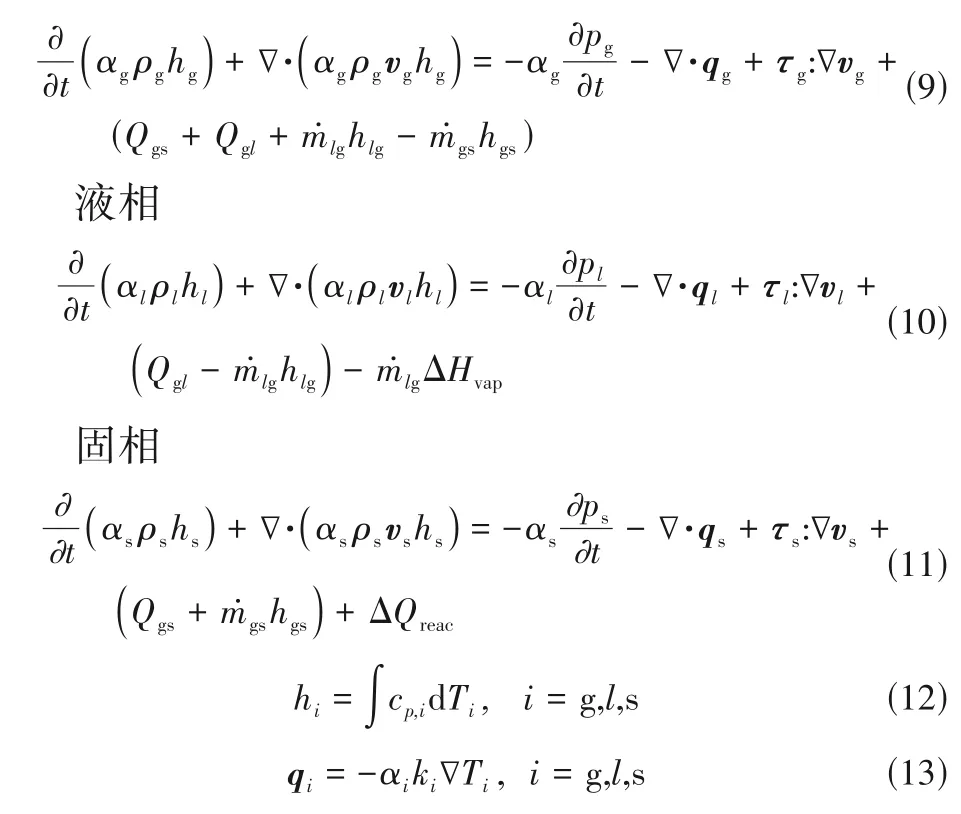

1.2 升力模型
在本次研究中,只考虑气固相之间的升力模型的影响,忽略了气液、液固之间的升力。在气固相之间作用在气相上的升力公式为:

式中,Clift是升力系数,由不同的升力模型决定。Saffman[31]将升力系数定义为颗粒Reynolds 数Rep和涡Reynolds 数Rew的函数,之后Mei 等[32]在此基础上将应用范围进一步扩大得到了Saffman-Mei 模型。在Legendre-Magnaudet 模型[33]中考虑了由流体界面处的流体摩擦/应力而引起的颗粒周围流动与流体颗粒内部再循环流动之间的动量传递,其中C2lift在低Reynolds 数和高Reynolds 数时取值不同。Moraga模型[34]是将粒子和粒子尾流引起的涡流相互引起的升力和空气动力引起的升力相结合,其升力系数也是由Rep和Rew表示。
Saffman-Mei模型:

1.3 聚合反应动力学
在聚合反应中,链增长的基元反应速率远大于其他基元反应,是聚合反应放热的主要贡献部分。因此在大多数研究中将聚合反应模型简化为只考虑链增长反应和催化剂失活基元反应[11]。
链增长反应:


1.4 液相蒸发模型
根据Pan 等[11]提出的液相蒸发模型,主要的方程如下:
气液相间的传热模型

在该模型中,只考虑液滴蒸发引起的液滴粒径的变化,忽略液滴聚并和破碎造成的影响,同时,为了简化模型,进入反应器的液滴由单一的平均粒径表示,液滴粒径为8×10-5m。
2 模拟条件和模拟方法
本文采用二维FBR 进行模拟,具体的几何尺寸见图1。流化床直径5 m,高度13.8 m,初始时刻颗粒以体积分数为0.5 在床层底部堆积,堆积高度为3.5 m。FBR 的网格划分和产生采用软件GAMBIT 2.3.16,选用四边形结构规整网格,网格尺寸为2.5 cm×1.25 cm,综合考虑计算精度和计算时间确定本文网格数为220800 个。FBR 中气、液、固相的性质、相关工业操作条件以及网格无关性检验在之前的工作[11]中叙述过,本文仍使用此前的参数值,具体见表1。文中CFD 耦合模型所有的方程组采用软件FLUENT 在双精度模式下求解,由外部自定义函数将液相蒸发相关源相、传热模型和聚合反应动力学耦合进模型中。液相体积分数在反应器入口指定,入口设置为气液相的速度入口,出口设置为压力出口。湍流模型为RNGk-ε模型,速度与压力耦合采用Phase Coupled SIMPLE 算法。气液相壁面设置无滑移,固相设置为部分滑移,镜面反弹系数设置为0.001。控制方程组的时间离散化均采用二阶迎风格式,模拟时间步长为0.001 s。具体的模型参数设置见表2。

表1 气、液、固三相的性质及工业操作条件Table 1 Physical properties of three phases and operation conditions from industrial data

表2 模型参数Table 2 Numerical parameters

图1 聚乙烯工业流化床反应器示意图Fig.1 Geometries of the simulated fluidized bed reactor
3 结果与讨论
3.1 床层压降
流化床的床层压降是其设计放大过程中的重要参数,受床层内的各相的体积占比影响。多相流体系中,气相对于床层压降的贡献很小,一般可以忽略。因此,气-液-固三相流化床的床层压降可以用式(53)描述:
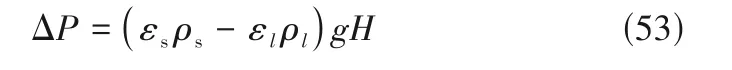
根据压降公式计算出床层压降为19238 Pa。图2 是根据理论方程和数值模拟得到的压降值。床层中颗粒的剧烈运动会使压降在一定范围内波动。Legendre-Magnaudet 模型在流化初始阶段颗粒回混现象明显,流化趋于稳定后颗粒运动稳定,因此其前期压降的波动情况较为明显。Saffman-Mei、Legendre-Magnaudet 和Moraga 模型各时刻(40~70 s)的床层压降平均值分别为:19293、19192 和19113 Pa,三种升力模型都很好地描述了床层的压降情况,验证了模型的有效性。Moraga 模型的时均压降值较低,Saffman-Mei 和Legendre-Magnaudet 模型的时均压降值与经典三相压降公式所得值相差不大,其中Legendre-Magnaudet 模型预测床层压降最为准确。

图2 FBR中流化过程的床层压降Fig.2 The pressure drop with the fluidization proceeding in the FBR
3.2 流化过程
图3 是固相颗粒粒径为5×10-4m 在三种不同升力模型下固相颗粒体积分数随时间的变化。从图中可以看出,随着不断进料的流体作用,推动了床层膨胀上升,促进了床层的均匀流化。随着流化的进行,在40 s时,各升力模型的床层高度基本都维持在同一高度不再改变,同时结合床层压降的分布可以认为各模型流化过程在40 s 后达到了稳态,此后相关变量不再发生改变。在流化起始阶段,床层内便生成了大量密集的气泡,在升力的作用下气泡向壁面移动使壁面附近固相颗粒分率逐渐降低,同时底部不断地进气使床层持续膨胀并向上涌动,促进床层颗粒流化。可以发现三种模型在相同时刻的床层平均高度基本一致,达到稳态时,床层平均高度均为12 m,说明升力作为横向力并没有影响床层的纵向膨胀涌动。

图3 不同升力模型流化过程Fig.3 Fluidization process of different lift models
升力会倾向于将较大的气泡推向中心区域,将较小的气泡推向壁面区域。从图中观察三种升力模型,可以发现流化的初始阶段(3~10 s)由于升力的影响造成了小气泡携带颗粒横向移动加剧,而床层底部进气推动床层向上移动,同时颗粒在壁面可以自由滑移,因此固相颗粒沿壁面上升流化更为明显。其中,Saffman-Mei 模型和Moraga 模型颗粒有明显的沿壁面上升的现象。部分气泡在流化过程中不断增大,形成的较大气泡在升力的作用下向中心运动,在移动过程中除受升力作用还有竖直方向曳力,液相组分的蒸发也促使气泡以旋涡方式流动的现象更为明显,其余较小气泡携带着流化的固相颗粒继续沿壁面向上移动至床层界面处,之后颗粒在气泡尾迹的影响下上升到高处并回落。在升力和壁面润滑力的作用下,沿着床层中心线左右两边径向方向床层的空隙率一般呈现出先增大后减小的趋势。观察流化过程的后期20、30、40 s的云层图像可以发现,由于升力的影响,流化的床层中含有大量旋涡状的气泡分布在近壁面处,而壁面处的固相颗粒体积分数依然很大。在流化过程中,由于气泡旋涡态的运动,使床层在流化过程中出现回流以及部分位置固相颗粒聚集的现象,影响了床层整体均匀流化。
在0~5 s时流化处于初始阶段,流化现象并不明显,床层颗粒高度变化较小,为了更为清楚地观察三种升力模型对于固相颗粒流化过程的影响,如图4 为选用6~10 s 作为研究时间段,3.5 m 床层下不同升力模型下固相体积分数径向分布情况。由图中可以看到,Saffman-Mei模型在壁面处及整体床层中的固相体积分数较小,在径向中心处固相颗粒聚集明显,在中心处两侧拥有较大的空隙率,说明生成较大的气泡在中心处聚集并推动床层向上膨胀;Legendre-Magnaudet 模型和Moraga 模型在壁面处的固相体积分数相近,但Legendre-Magnaudet 模型床层整体颗粒分布更为均匀且中心处颗粒体积分数明显高于其他两种模型,结合图3 可以看到床层中心位置回混严重;Moraga 模型固相颗粒体积分数波动较大,颗粒运动剧烈,壁面处颗粒体积分数大,颗粒集聚明显,同时右侧近壁面处空隙率较大,体积分数梯度大。

图4 流化过程中固相体积分数径向分布Fig.4 Radial distribution of solid phase volume fraction in the fluidization process
结合图3和图4,可以发现在流化过程中升力模型对于固相颗粒流化影响明显,Saffman-Mei 模型下,颗粒沿壁面上升明显,颗粒在床层上方和中心处聚集,形成气泡较小且均匀;Legendre-Magnaudet模型下颗粒的回混现象严重,中心处颗粒聚集明显,会使得反应器前期压降变化波动大;而Moraga模型会促使颗粒横向运动加大,促进颗粒向壁面处聚集,在近壁面处形成较大空隙率。
图5 和图6 是三种不同粒径固相颗粒在Saffman-Mei 模型下的流态化过程和固相体积分数径向分布(3.5 m床层高度下)。起始流化阶段,小粒径颗粒体积小,被进口处的气液相推动向上膨胀,生成较大气泡,气泡主要在床层中心区域运动并造成回混,因而此区域固相体积分数迅速降低。由于颗粒粒径较小部分区域气泡中固相体积分数几乎为零,整体体积分数较小,且短时间内便流化均匀。颗粒粒径较大的纵向膨胀较慢,在升力的影响下壁面附近产生了更为明显的固相颗粒聚集现象,近壁面处有着较大的体积含量梯度;同时,床层下部整体体积分数较大,且颗粒体积分数波动和振幅较小,内部生成的气泡较小。

图5 不同粒径固相颗粒在Saffman-Mei模型下的流化过程Fig.5 Fluidization process of different particle sizes in Saffman-Mei model
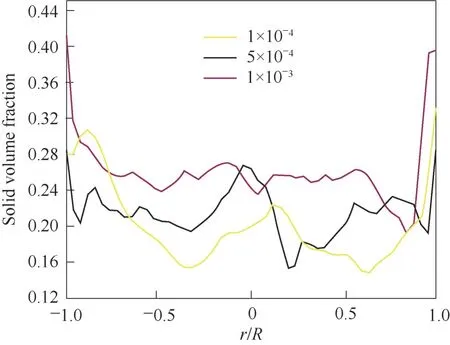
图6 不同粒径颗粒在Saffman-Mei模型下流化过程中固相体积分数径向分布Fig.6 Radial distribution of solid phase volume fraction in Saffman-Mei model fluidization process for different particle sizes
3.3 固相体积分数分布
根据前面流化过程确定40 s 后床层达到了稳态,可以认为相关变量不再改变,因此选用40~70 s做时均化处理。
从图7 可以看到在流化稳定后,床层平均高度基本稳定在了12 m,在不同高度下颗粒运动存在一定区别,因此分别研究了床层高度在0~3.5 m、3.5~8.0 m、8.0~12.0 m 以及0~12.0 m 下的时均化的固相体积分数径向分布情况,结果见图8。

图7 固相体积分数轴向分布Fig.7 Axial distribution of solid volume fraction
在床层高度0~3.5 m 的情况下,三种模型固相体积分数径向分布相似,Legendre-Magnaudet 模型的轴向体积分数略微大于其他两种模型,同时在中心处颗粒聚集明显,在近壁面处的体积分数梯度较小,振幅较大,说明在区域内中心附近产生了较大的气泡,颗粒在此高度下发生回流。在床层高度3.5~8.0 m 的 情 况 下,Legendre-Magnaudet 模 型 和Moraga 模型径向分布较为一致,体积分数波动多但振幅较小,没有较大的空隙率梯度,说明这两种模型在此区域内的颗粒运动均匀,产生的气泡较小,而Saffman-Mei 模型在床层左侧存在较大的空隙率梯度且体积分数低于另外两种模型,说明在此区域内的颗粒运动较为剧烈,左侧存在较多较大气泡。当床层高度为8.0~12.0 m 时,Saffman-Mei 模型的径向体积分数较为平缓且轴向体积分数高于另外两种模型,颗粒运动较为均匀,颗粒在此高度范围内聚集现象强;而Moraga 模型径向体积分数波动较多,振幅较大,在此高度下产生了许多较大的气泡。
由图7 和图8(d) 可以发现,不同模型对颗粒轴向分布和运动状况影响不同,但三种模型的固相颗粒均呈现了在中心处与壁面处聚集的现象。Saffman-Mei模型固相在床层中、高部分聚集并且运动明显,在近壁面处易于产生较多较大的气泡;Moraga 模型在不同高度处的近壁面处都表现出了较大的固相体积分数梯度,易于使壁面处发生较为强烈的固相颗粒聚集,内部体积分数波动幅度较大,床层内部也存在较多的大气泡影响固相颗粒的分布。Legendre-Magnaudet 模型对于固相颗粒的运动影响较为均匀,不论在近壁面处还是床层内部固相的体积分数分布波动都较小,结合压强分布,说明在Legendre-Magnaudet 模型下流化稳定后,床层内部将产生较小且均匀的气泡。

图8 固相体积分数径向分布Fig.8 Radial distribution of solid volume fraction
3.4 液相蒸发速率
反应器内部是气-液-固三相流流体流动,在床层内存在液相的蒸发,需要考察不同升力模型对于液相蒸发的影响。从图9中可以看到,在流化初期,液相的蒸发速率为零,这是因为前期床层温度低于液相的蒸发温度333 K。随着流化进行,床层温度升高,液相开始蒸发并逐渐加快。Saffman-Mei模型和Moraga 模型蒸发速率几乎相同并高于Legendre-Magnaudet 模型,随着模拟的进行,速率差距不断增大。

图9 FBRs中液相蒸发速率Fig.9 Evaporation rate of liquid phase in FBRs
3.5 固相颗粒温度分布
在FBR 中发生了聚合反应放热,应当记录床层的温度分布情况。由于进料的气液相温度为328 K,与流化稳定的床层内部存在较大的温差,因此在进口处具有明显的梯度,而床层的中、高部分温度几乎趋于一致,因此本文研究了不同时均条件床层高度为0~3.5 m区域内的温度分布情况。
图10 是三种升力模型在不同时刻的固相颗粒径向温度分布情况。乙烯的聚合反应是发生在固体颗粒表面的强放热反应,高浓度的固体颗粒代表着更高的热量在此集聚,而液相蒸发会吸收大量热量,更高的空隙率也会更快地进行传热。由于固相颗粒在壁面处聚集,进入反应器的气液相主要在床层中心附近与固相反应换热,三种模型在稳定后时均化时间内径向温度分布相似,均表现出了中心附近温度较低,壁面温度高。其中Saffman-Mei 模型的温度略微低于其他两种模型,壁面处存在较大温度梯度,结合固相体积分数可以发现这是由于Saffman-Mei模型下颗粒向床层中、高处及壁面运动而造成的影响。在40~50 s 时间内,Legendre-Magnaudet 模型径向温度分布为明显的“V”字形分布,此后的51~60 s 与61~70 s 中该模型的最低处温度分布也在中心处附近,轴向两侧温度分布也相对对称,证明气液相集中在中心处与固相换热,颗粒流化稳定主要在壁面处集聚。由图10(a)、(b)可以发现Moraga 模型最低处温度偏移中心,床层两侧温度分布不对称,说明颗粒及气泡运动剧烈,导致气液相不同时刻在不同位置与固相颗粒反应换热,低温区域范围较宽,气液相与固相换热范围大,颗粒流化较好,随着流化的持续进行该模型的径向温度分布趋于稳定,低温范围集中。
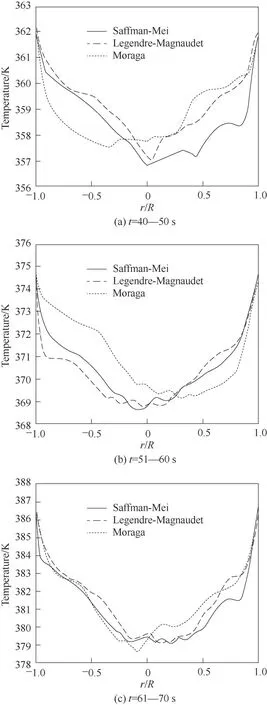
图10 FBR中固相颗粒径向温度分布Fig.10 Radial temperature distribution of solid phase particles in FBR
4 结 论
在聚乙烯流化床反应器中,考虑了液相在床层内蒸发对于流型的影响,探究了气固相之间分别应用Saffman-Mei 模 型、Legendre-Magnaudet 模 型 和Moraga 模型对于FBR 中三相流动力学行为和相分布特性的影响,主要结论如下。
(1)三个模型都可以很好地预测床层压降,Saffman-Mei 模型和Legendre-Magnaudet 模型预测床层压降值与经典压降公式计算结果相近,其中Legendre-Magnaudet模型预测值最为准确。
(2)不同粒径的固相颗粒在升力影响下流化过程存在一定差别,小粒径模型易于产生较大气泡在床层中心区域运动造成回混,粒径越大颗粒在壁面处的聚集情况更为明显。
(3)不同的升力模型对于流化稳定后的床层高度、床层平均温度没有显著影响,在固相颗粒的径向分布和床层内部温度分布存在差异。Saffman-Mei 模型在床层中、高部分运动差异较大,床层底部温度较低;Moraga 模型易产生较大气泡带动颗粒运动剧烈;Legendre-Magnaudet 模型初始流化过程中存在较强回混,前期压降变化剧烈,但整体运动均匀,具有良好的稳定性。
(4)升力模型对于FBR 内液相蒸发存在影响。Saffman-Mei 和Moraga 模型蒸发速率几乎相同并高于Legendre-Magnaudet 模 型,Legendre-Magnaudet模型反应器内部液相蒸发分布较为均匀。
符 号 说 明
Clift——升力系数
ds,dl——分别为颗粒、液滴的直径,m
e——恢复系数
Flift——气固相间升力,kg·m2·s-1
g——重力加速度,m·s-2
ΔH——聚合反应热,kJ·mol-1
ΔHvap——异戊烷的汽化潜热,J·kg-1
hg,hs,hl——分别为气相、固相、液相的比焓,kJ·kg-1·K-1
I——单位矩阵
I2D——偏应力张量的第二不变量
Klg,Ksg,Kls——分别为气液相间、气固相间、液固相间的作用力,kg·m2·s-1
kd,kd0——分别为催化剂失活反应速率、失活反应速率常数,s-1
kp,kp0——分别为反应速率、反应速率常数,m3·mol-1·s-1
ṁlg,ṁgs——分别为液气、气固相间的传质速率
Nus,Nu*——分别为固相、液相蒸发Nusselt数
Ps——固相压强,Pa
Pr——液相Prandtl数
Qgs,Qgl——分别为气固相间、气液相间的热交换量,W·s-1·m-3
qg,qs——分别为气相、固相的热交换密度,W·m-2
Rd——液滴蒸发率,kg·s-1
Rp——聚合速率,mol·m-3·s-1
Re——Reynolds数
Tamb,Tg,Ts,Tl——分别为环境、气相、固相、液相的温度,K
vg,vs,vl——分别为气相、固相、液相的速度,m·s-1
αg,αs,αl——分别为气相、固相、液相的体积分数
μg——气相黏度,Pa·s
μs——固相的剪切黏度,Pa·s
μs,col——固相的碰撞黏度,Pa·s
μs,kin,μs,fr——分别为固相的运动黏度、摩擦黏度,Pa·s
Θs——颗粒温度,m2·s-2
γs——能量的碰撞耗散,m2·s-2
τg,τs——分别为气相、固相的剪切应力,N·m-2
ρg,ρs,ρl——分别为气相、固相、液相的密度,kg·m-3
λs——固相体积黏度,Pa·s
下角标
g——气相
l——液相
s——固相
