改进加权匹配追踪信道估计算法
2022-02-18吕治国邵鸿翔
吕治国,齐 萌,邵鸿翔
(洛阳理工学院 计算机与信息工程学院,河南 洛阳 471023)
0 引 言
通信系统增加天线能减小热噪声对系统性能的影响[1-3],但需要发送端提前获取信道信息。然而信道估计在大规模天线场景下实施困难,可利用信道互易性估计信道存在的导频污染[4]。由于信道表现出稀疏或接近稀疏的特点[5-6],可用压缩感知技术完成信道估计[7-9],而常用的匹配追踪(Matching Pursuit, MP)算法估计速度和精度不能满足要求。文献[10]改进了MP算法,采用变步长梯度追踪算法估计信道,由残差和梯度计算权值;文献[11]提出了加权自适应正交MP算法,以残差信号模的倒数作为权值,但加权处理反而会降低高信噪比(Signal Noise Ratio,SNR)情况下的信道估计精度;为此,文献[12]提出了分段处理方案,限制算法应用SNR范围。以上加权算法有如下缺点:所用权值不是最优值;权值计算方法不完善;依据SNR划分实施区域的实际操作困难。
文献[13]利用双贪婪追踪算法获取信号特征,加权后可提高信道估计精度。利用信道在角度域上的不均匀性[14],或利用信道元素的频谱信息特征[15],对估计信号进行加权也能提高估计精度。本文提出了一种改进算法,根据估计信号与误差的比例关系计算权值,且让权值随着迭代次数增加,能保证低SNR条件下的估计精度,同时还改善了高SNR条件下的估计精度性能。
1 系统模型描述
大规模多输入多输出(Multiple-In Multiple-Out,MIMO)系统中的基站配备多根天线。越来越多的终端也配备了多天线。终端与基站之间的信道用高维矩阵表示。假设矩阵矢量化后维数为N,实际信道可用一个N维矢量h来表示。基站发射导频,终端收到的信号y为
式中:A=[A(1) ,A(2) ,…,A(Lp)]T为导频信号矩阵,矩阵A维数为Lp×N,Lp为每一根基站天线发射导频信号的长度;n为加性高斯白噪声矢量。矢量n维数为Lp×1,n中的元素服从0均值、方差为σ2的高斯分布。假设研究的信道是直接表现出稀疏特性的信道。稀疏信号中非零值的个数K被定义为稀疏度。信道h可表示为
式中:ha为列矢量,其每个元素都是随机变量,具体分布取决于实际的信道,表示信道元素概率分布情况;⊙为哈达玛乘积;hb也为列矢量,其元素服从伯努利分布,非零概率为p,表示信道稀疏特性。信道稀疏性与信道元素概率分布情况分离,减小了信道估计的难度。
2 分析与讨论
借助于MP算法,信道可以用短导频信号来估计,即N维稀疏信道矢量信号h能由M维观测值y来估计:
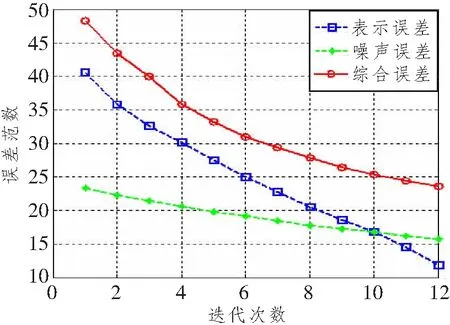
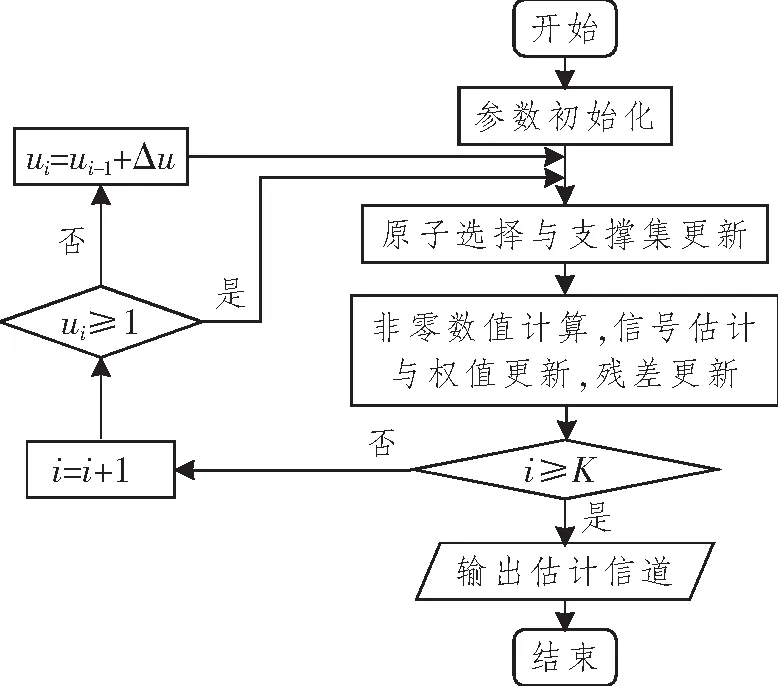
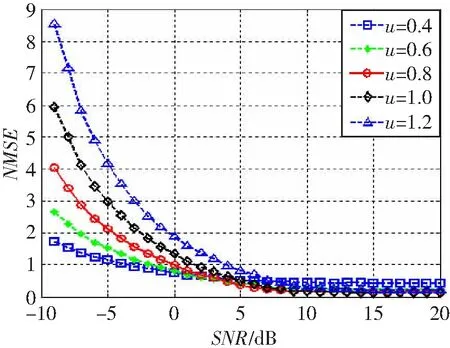
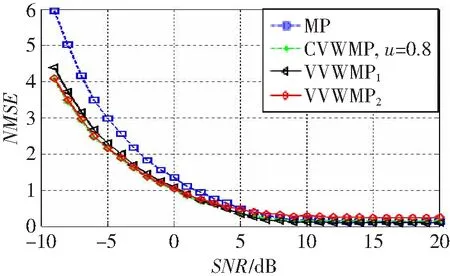
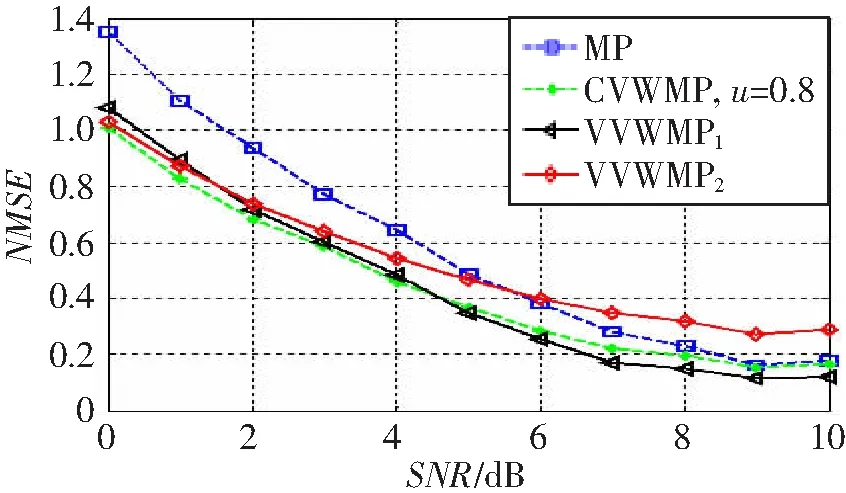
式中:Φ为观测矩阵,大小为M×N且M 图1 各种误差随迭代次数变化趋势 根据误差变化规律,可以让权值随迭代次数的增加而增加,且保证最后一次迭代中的权值增加到1来提高估计性能。改进加权MP算法的流程图如图2所示。 图2 改进加权MP算法流程图 算法的主要处理步骤解释如下: (1) 参数初始化 (2) 原子选择与支撑集更新 观测矩阵Φ的列称之为原子,找出与残差信号内积最大原子在Φ中对应的索引λ(i): 式中,|〈a,b〉|为两个矢量内积的绝对值。把λ(i)和已经找到的原子索引集合Λi-1合并,组成当前迭代支撑集Λi,即Λi=Λi-1∪{λ(i)}。 (3) 非零数值计算 (4) 信号估计与权值更新 若权值ui≤1,则将ui增加Δu,否则就设为1。 (5) 残差更新 若条件i≥K得到满足,则迭代结束;否则i=i+1,重复步骤(2)~(5),直至i≥K。 (6) 输出估计信道 本文所提算法的最大贡献就是对新增估计值进行加权并使权值随迭代次数变化。 信道估计算法的估计精度性能,可通过计算其归一化均方误差(Normalized Mean Square Error, NMSE)μNMSE来衡量: 权值u保持不变的加权算法称之为固定加权MP(Constant Value Weighted MP, CVWMP)算法。u的大小由信道数据训练得到。我们先来测试不同加权值对信道估计精度的影响。仿真中将矢量化后的稀疏信道矢量h的维度设置为256。列矢量hb中每一个元素是随机变量,服从伯努利分布,非零概率为0.05。图3所示为CVWMP算法采用不同固定加权值的估计性能,权值等于1就是标准MP算法。由图可知,随着权值由0.4增加到1.2,NMSE先变小后变大。通过设置合适的加权值,可以提升低SNR区域的估计性能,但无法改善高SNR区域的估计性能。通过信道训练可以找到针对特定信道环境下合适的加权值。采用这个经验加权值,可以提高在低SNR条件下的估计精度,同时基本不损害在高SNR条件下的估计精度,该仿真条件下最优的权值up=0.8。 图3 不同权值CVWMP算法估计性能比较 即使采用最优权值,也只能改善低SNR情况下的估计性能,并损害高SNR情况下的估计性能。通过给各次迭代中得到的元素估计值设置变化的权值重构算法来解决这个问题。这种变化权值的重构算法称为变化加权MP(Varying Value Weighted MP, VVWMP)算法。该算法具体处理过程与CVWMP算法类似,只是每次迭代中的权值会发生改变。在与测试CVWMP算法性能相同的环境中,我们测试不同变化权值对VVWMP算法估计精度性能的影响。图4和5分别给出了宽和窄SNR范围条件下,采用固定加权值、变化权值以及原始MP算法的估计精度性能比较。CVWMP算法中固定权值采用u=0.8;VVWMP1算法中权值初始值为u=0.6,每增加一次迭代,权值增加0.05;VVWMP2算法中权值初始值为u=1,每增加一次迭代,权值减少0.05;为了公平,两种算法权值平均值相同。权值改变量Δu由迭代次数和权值初始值决定。迭代次数用估计信号的稀疏度K代替。初始值由CVWMP算法测试得到的最优权值up决定,大小等于2up-1,权值改变量Δu由下式计算: 图4 宽SNR范围条件下不同算法估计性能比较 为保证最后一次迭代权值达到1,实际Δu要乘上大于1的修正因子β,这里β=1.6。 由图4可知,相比于原始MP算法,CVWMP和VVWMP算法在低SNR条件下都能获得估计精度性能上的提升。为了更清楚地显示各种算法的优劣,我们在图5中给出了窄SNR范围内各种算法估计精度的比较。由图可知,采用逐步变大权值的VVWMP1算法,无论在高SNR还是在低SNR条件下,估计精度都优于MP算法,这是依靠随迭代次数线性改变权值而获得的。采用逐步减小权值的VVWMP2算法,除了在低SNR区域有微小性能提升外,在大多数情况下都表现最差。 图5 窄SNR范围条件下不同算法估计性能比较 针对MP算法对大规模MIMO系统信道估计不准的问题,本文对MP算法进行改进,提出了一种对每一次迭代计算中估计出的信道值设置权值的信道估计算法。通过设置权值,可以更大概率获取准确的原子,提高估计精度或减少计算量,实现准确度和计算速度的均衡。根据估计信号、残差信号、表示误差和噪声误差随迭代次数的变化规律,让权值随迭代次数的增加而增加,最终增加到1的调整方法可以在更宽的SNR范围内改善信道估计精度性能。通过实验仿真证明了改进算法的有效性。
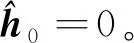
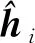
3 实验研究
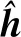
4 结束语
