面向电力物联网的5G移动边缘计算任务卸载方法

毛水强，洪健，任华，马骁，徐勇军

(国网金华供电公司，浙江 金华 321001)

0 引 言

电力物联网是先进信息通信技术在电力行业的深度推广应用，一经提出便得到广泛的理论研究与应用推广，电力物联网可以有效整合通信与电力基础设施资源，提升电力系统的信息化与智能化水平，为电力的发、输、配、变、用、调度等环节提供强有力的技术支撑[1]。随着电力物联网建设的持续推进，海量数据采集终端被部署在电力生产与传输的各场景中，为各类电力业务的正常开展提供数据基础。结合电力物联网实际的业务场景及业务需求，这些数据需要经过进一步地分析处理，例如故障检测、故障点定位等。这些计算密集型任务往往对时延和可靠性等服务质量(Quality of Service, QoS)有着严格的要求，仅依靠计算资源受限的本地终端或数据机房进行处理几乎不可能实现[2]。云计算范式在电力行业的应用由来已久，然而，传统云计算中心主要位于距离电力现场较远的中心机房，对跨区域网络部署的完善性要求较高，且极易发生传输中断或链路拥塞的情况，已难以完全满足电力物联网计算任务的实时性和可靠性处理需求[3-4]。

作为5G关键技术之一的移动边缘计算(Mobile Edge Computing, MEC)为上述问题提供了一种可行的解决方案。MEC的概念最早由欧洲电信标准化协会(European Telecommunications Standards Institute, ETSI)在2014年提出，与云计算的不同之处在于，MEC将计算能力进一步下沉至网络边缘，能够在靠近无线接入网(Radio Access Network, RAN)侧提供快捷、可靠地计算服务[5]。而计算密集型任务的卸载问题一直以来便是MEC相关技术中的研究热点，如何将任务的时延和可靠性等需求与网络边缘侧相对受限的通信和计算资源进行统筹考虑，制定合理的卸载方法仍然是一个开放性的问题[6]。在目前的研究工作中，来自新泽西理工学院的研究团队针对边缘/雾计算中的工作负载均衡问题，提出一种与设备相关联的分布式算法以最小化通信与计算的等待时延[7]，并在后续研究中进一步将之扩展到无人机辅助通信的系统中[8]。文献[9]从服务器资源高效利用的角度出发，在不降低业务应用质量的基础上通过对前端数据进行压缩和多服务器的协同来减小数据冗余、节省网络成本。文献[10]将机器学习算法应用在车辆边缘计算系统中，通过智能体对网络环境的实时感知和学习不断优化卸载决策，以最小化长期平均时延。文献[11]将最优卸载决策制定为一个马尔科夫决策过程，并采用值迭代算法进行求解，以降低任务卸载的总时延。

然而，现有研究大多针对5G公网或车联网场景，与电力物联网的业务场景和业务需求并不完全适配，面向电力物联网的5G移动边缘计算任务卸载方法仍面临如下挑战：

(1)复杂多变的网络拓扑及网络环境：电力物联网中数据采集终端分布广泛，且具有一定的移动性。另一方面，无线信道的信道状态信息(Channel State Information, CSI)及网络中数据采集量都具有高度的时变性，且各类电气设备在工作时会向环境中辐射电磁噪声，导致传统公网的干扰模型不再适用。因此，如何结合网络实时信息对不同终端卸载决策进行动态优化和调整是一个需要直面的挑战；

(2)差异化的电力业务需求：电力物联网所承载的电力业务可分为保护控制类、信息采集类、移动应用类等，不同类型的业务往往具有不同的优先级，例如保护控制类业务包含电网安全稳定运行的关键信息，优先级往往最高。在实际的任务卸载决策时，应当优先保证此类高优先级业务的性能，以避免对电网运行造成危害；

(3)通信、能耗与计算资源的联合优化：包括电力物联网在内的任务卸载问题往往面临多维度资源的联合优化问题，通信、能耗及计算资源的相互耦合为优化问题的求解带来巨大挑战。因此，如何通过合理的优化机制设计，即降低优化问题求解的复杂度，同时实现多维资源的联合优化是面临的另一个挑战；

(4)资源受限场景的多终端竞争模式：实际的电力物联网接入场景中，信道资源往往受限，边缘服务器与云服务器相比，计算资源也相对紧张，各终端为实现自身性能的优化往往会倾向于占用更好的信道和计算资源，如何从网络整体性能提升的角度协调各终端的卸载决策仍亟待解决。

针对上述问题和挑战，文章主要工作总结如下：

(1)建立电力物联网整体网络模型，对其中的数据传输处理时延、能耗进行量化分析，设立与时延和业务优先级相关的优化目标及长期能耗约束；

(2)借助Lyapunov优化的在线执行特性，将长期时延优化问题和长期能耗约束转化为一系列短期的确定性优化问题，并给出优化问题有界性相关的理论分析；

(3)改进基于梯度价格的拍卖算法对计算任务卸载策略进行优化，同时解决多终端的卸载策略冲突问题，在提升网络整体效用的同时实现纳什均衡；

(4)通过与传统任务卸载方法的仿真对比，验证文中所提算法在时延、能耗等方面的优越性能。

1 系统模型

该节主要介绍融合5G移动边缘计算的电力物联网系统模型，并对其中的通信、能耗、计算模型展开分析。文章采用的系统模型如图1所示，主要由电力物联网数据采集终端、基站、服务器等要素组成。基站可为覆盖范围内的终端提供无线覆盖，并搭载有服务器，为卸载到基站的计算任务提供计算服务。该场景包含M个数据采集终端，被定义为集合M={1,…,m…,M}。文章采用时隙模型[12]，整个时间周期被划分为T个时隙，被定义为集合T={1,…,t…,T}。每个时隙开始时，每个数据采集终端会产生一个数据量大小为Am(t)的待处理任务，且服从[Am,min,Am,max]之间的随机分布，当网络中所有任务完成传输和计算后，下一个时隙开始。可供选择的无线信道共有N个，被定义为集合N={1,…,n…,N}，不同的信道间采用正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)方式进行调制，即彼此间无干扰[13]。MEC服务器的计算资源被划分为K个，单个资源块每个时隙可提供的CPU频率为fk(t)，且服从[fk，min,fk,max]之间的随机分布[14]。

图1 系统模型Fig.1 System model

设置计算任务卸载中的信道选择决策指示变量和计算资源块选择决策指示变量分别为xm,n(t)和xm,k(t)。当xm,n(t)=1时表示终端m在第t个时隙时选择信道n进行任务卸载，否则xm,n(t)=0。同理，当xm,k(t)=1时表示终端m在第t个时隙时将计算任务卸载至第k个计算资源块，否则xm,k(t)=0。为保障任务传输和计算性能，单个信道和计算资源块在单个时隙内至多可以分配给一个终端使用。此外，考虑到计算任务的不可分割性，单个终端在单个时隙内至多可以选择一个信道和一个计算资源块进行任务传输和处理，即满足：

(1)

(2)

1.1 通信模型

假设在单个时隙内数据采集终端到基站的距离δm,n(t)保持不变，则第t个时隙时，终端m选择信道n进行任务卸载的传输速率可以被表示为：

(3)

(4)

需要注意的是，任务处理完成后的回传时延并未被考虑在内，原因在于回传结果相对于原始数据相对较小，可以被忽略[16]。

1.2 能耗模型

第t个时隙时，终端m选择信道n进行任务卸载时的传输能耗被表示为：

(5)

电力物联网场景中一个不可忽视的问题是数据采集终端携带的电池容量往往有限，为避免频繁的电池更换，在进行任务卸载优化策略制定时必须将长期能耗约束考虑在内，以避免因频繁的电池更换而导致的业务传输中断问题[17]。长期能耗约束被表示为：

(6)

式中Em,max表示终端m用于数据传输的最大能量预算。

1.3 计算模型

文章采用一个经典的计算模型去描述所要进行处理的计算任务，除上文中提到的任务数据量大小Am(t)之外，还包含任务的计算复杂度γm，表示计算1 bit任务数据所需要的CPU频率[18]。则第t个时隙时，终端m选择计算资源块k进行任务卸载的计算时延，可以被表示为：

(7)

2 问题建模与转化

该节主要介绍优化问题的建模与转化过程，并通过理论分析证明优化问题的有界性。

2.1 问题建模

通过上述分析，第t个时隙时，终端m选择信道n和计算资源块k进行任务卸载的总时延可以表示为：

(8)

文章的优化目标为在长期能耗约束条件下，考虑不同终端所承载业务的优先级ηm，最小化整个网络的长期平均卸载时延，可被建模为如下的一个二值变量优化问题：

(9)

式中C1和C2分别表示信道选择和计算资源块选择约束；C3表示长期能耗约束；决策变量为{xm,n(t)}和{xm,k(t)}。

2.2 问题转化

由于长期优化目标和长期能耗约束C3的存在，导致优化问题P1很难被直接求解，因为有关未来时隙的任务量大小、CSI、计算能力等信息对于终端都是难以获得的。为解决该问题，文章借助Lyapunov优化的方法将上述问题转化为一系列短期优化问题。Lyapunov优化方法由美国斯坦福大学Michael J. Neely提出，是一种不需要先验证统计信息和未来信息的在线优化算法[19]。

基于Lyapunov优化中虚拟队列的概念，可以将长期能耗约束转化为一个虚拟队列Hm(t)，该队列被命名为能量赤字队列，即截止当前时隙借用预留给未来进行数据传输的能量大小，且满足Hm(1)=0。其随时隙的变化情况被表示为：

(10)

综上所述，原始的长期优化问题P1最终被转化为如下的一系列短期卸载决策问题：

(11)

式中V表示时延与能耗之间的折中系数，V越大，表示越倾向于优化时延。从上述优化问题中还可以看出，当能量赤字队列增大时，优化目标中能耗的比重会对应增加，则会更倾向于优化能耗。

2.3 性能分析

需要注意的是，优化问题P1和P2并不是完全对等的，P2求解后的卸载决策与P1求解后的最优卸载决策之间会存在一定的偏差，但通过设置虚拟能量队列，可以尽可能保证长期能耗约束的满足[20]。通过数学推导，可以证明单个终端的平均时延应当满足：

(12)

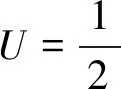
(13)

单个设备的总能耗应当满足：

(14)

由于篇幅限制，文章并未给出详细证明，但是相类似的证明过程可以在文献[19-20]中被找到。上述结果从理论上证明时延与能耗之间存在着[O(1/V),O(V)]的折中关系，通过调整V，可以实现时延与能耗之间的折中。

3 算法设计

该节主要介绍如何利用基于梯度价格的拍卖算法来求解优化问题P2。

3.1 拍卖算法简述

如上所述的卸载决策问题可以被视作一个经典的分配问题，每个终端都可以被视作一个“自私”的买家，他们都倾向于去占用更优的信道和更多的计算资源来处理自己的计算任务，那么必然出现多个终端选择同一信道或者同一计算资源块的现象，即发生卸载冲突。而拍卖算法最早由Dimitri P. Bertsekas教授提出，常被用于解决这样的资源分配问题[21]。选用基于梯度价格的拍卖算法进行问题的求解，并在初始报价和梯度价格设定上结合电力物联网实际场景加以改进，可体现不同优先级设备的竞争力差别。类似于现实中的拍卖过程，该算法基本思想为各个买家在底价基础上通过不断地加价来排除竞争对手，直至获得该物品的所有权。

3.2 ABDE-TO算法

文章所提基于拍卖理论(Auction Theory-Based)、并可以有效实现时延(Delay)与能耗(Energy)之间折中关系的任务卸载(Task Offloading)算法被命名为ABDE-TO算法。详细的求解过程可以分为初始化阶段、竞拍阶段和卸载阶段。

ABDE-TO算法流程介绍如下:

(1)循环：fort=1:T;

(2)阶段一：初始化阶段;

(3)每个终端对不同资源块的初始报价被设置如下：

Qm,n,k(t)=Vηmdm(t)+Hm(t)Em,n(t)

(15)

(4)各终端根据对不同资源块的初始报价确定自己的拍卖次序表，初始报价越小，资源块的排序位置越靠前;

(5)每个终端向自身拍卖次序表中排序最靠前的资源块发起卸载请求;

(6)阶段二：竞拍阶段;

(7)循环：while 存在卸载冲突时(如前所述，资源块中任一元素被多个终端同时选择);

(8)发生卸载冲突的所有终端同时在初始报价的基础上按照一个虚拟的梯度价格提高报价，即：

Qm,n,k(t)=Qm,n,k(t)+ΔIm

(16)

(9)若此时有终端的报价超过其拍卖次序表中第二次序资源块的报价，则该终端退出此次拍卖，并将该资源块从自身拍卖次序表中删除;

(10)依据式(16)重复报价过程，直至仅剩一个终端时，该资源块完成分配;

(11)所有终端继续向其当前拍卖次序表中最靠前的资源便发起卸载请求;

(12)重复上述过程，直至不再有卸载冲突现象的发生;

(13)end while;

(14)阶段三：卸载阶段;

(15)所有数据采集终端使用其拍卖次序表中最靠前的资源块进行任务的传输与处理，卸载完成后依据式(10)更新能量赤字队列;

(16)end for。

上述基于梯度价格的拍卖算法可以被划入非合作博弈的范畴，并可以达到纳什均衡，即如果任意一个终端在其他所有终端的卸载策略确定的情况下，其选择的策略是最优的[22]。

4 仿真结果及分析

该节主要介绍仿真参数的设置，并通过合理设置对比算法来说明文章所提算法的优越性能。

4.1 仿真参数设置

文章采用MATLAB进行实验场景的仿真模拟，以单小区作为基本的仿真场景，基站的覆盖半径为1 km，每个时隙内数据采集终端的位置随机生成，每个设备的优先级被随机给定。每个时隙开始时，网络控制器会收集网络中的设备侧、信道侧、服务器侧信息，并依据ABDE-TO算法获得任务卸载决策，设备根据下发的卸载指令选择对应的资源块进行任务卸载，卸载完成后，反馈时延、能耗等相关性能数据。具体仿真参数设置如表1所示[5, 7, 15, 20]。

表1 仿真参数Tab.1 Simulation parameters

文章通过与启发式的原始算法进行对比来说明所提方法在时延、能耗性能方面的优越表现，具体对比算法设置如下：

(1)EO-TO(Energy-optimal Task Offloading)：该算法框架下，仅将任务卸载的传输能耗(与传输时延的最小化一致)作为优化目标[23]，而计算资源块的分配被随机给定，优化方法仍选用基于梯度价格的拍卖算法；

(2)DO-TO(Delay-optimal Task Offloading)：该算法框架下，仅将任务卸载的总时延作为优化目标，而长期能耗约束未被考虑在内[24]，优化方法仍选用基于梯度价格的拍卖算法；

(3)R-TO(Random Task Offloading)：该算法框架下，不同终端信道和计算资源块的分配均被随机给定。

4.2 仿真结果

不同算法下单个终端累计平均时延和累计能耗的对比情况如图2和图3所示。对于DO-TO算法，其时延表现最优，但是在大约第440个时隙会发生传输中断的现象，结合图2发现此时终端累计能耗已达能量预算的上限，说明该算法仅以时延优化为目标，会不加以节制的使用能量，因而从短期来看尽管时延性能略优，但会造成终端能量过早耗尽，无法继续进行数据传输。对于EO-TO算法，尽管其能耗消耗更低，但是时延性能也要更差，因为该算法仅以能耗优化为目标，导致使用能量过于保守，无法有效提升时延性能。对于R-TO算法，因为是完全随机的情况，因此其时延和能耗性能都表现很差，且能量预算耗尽的更快。而对于文中算法，前期能量充足时该算法会倾向于优化时延，而随着能量的减少，该算法可以通过计算时延与传输时延的联动，以适当牺牲时延的方式保障能耗性能，因此可以实现时延与能耗之间的权衡。

图2 不同算法下累计平均时延对比情况Fig.2 Contrast of cumulative average delay among different algorithms

图3 不同算法下累计能耗对比情况Fig.3 Contrast of cumulative energy consumption among different algorithms

ABDE-TO算法下时延与能耗的折中关系如图4所示，即权重参数V对平均时延和总能耗的影响(仅改变权重V，其余仿真参数保持不变)。通过将V从0.01增加到10，采用ABDE-TO算法的平均时延减少，而累计能耗增加，因为V越大，时延在优化目标中所占的比重更高，时延与能耗的折中大约在lg(V)=-0.15时实现，此时V≈0.7。从图4中还可以看出，时延和能耗性能随权重的变化基本遵循[O(1/V),O(V)]的折中关系，这也验证上文的性能分析部分。该结果也可以为实际优化问题的求解提供理论指导：在不同情况的能量预算下，应当如何合理选择V以确保在满足长期能耗约束的情况下尽可能降低时延。

图4 ABDE-TO算法下时延与能耗的折中关系Fig.4 Compromise relationship between delay and energy consumption based on ABDE-TO algorithm

5 结束语

文章面向电力物联网场景，引入5G移动边缘计算实现计算任务的就近处理，提出一种基于拍卖理论的计算任务卸载方法，该方法可以实现通信、能耗及计算资源的联合分配与优化，并解决多终端的卸载冲突问题，在满足长期能耗约束的基础上最小化任务的平均传输和处理时延。仿真结果表明，相对于传统任务卸载方法，文中方法有效地实现多维度资源联合分配，并可以实现时延性能与能耗性能之间的折中。在今后研究中，将继续结合先进的人工智能算法，探索在信息不确定情况下的任务卸载机制。