基于贝叶斯与数据驱动的智能电能表状态感知技术研究

2022-02-18马红明李倩陶鹏史轮马笑天冯波

电测与仪表 2022年2期

马红明，李倩，陶鹏，史轮，马笑天，冯波

(国网河北省电力有限公司电力科学研究院，石家庄 050000)

0 引言

智能电能表的稳当性相对于国家电网电力信息采集系统的稳固、安定、经济运转能力来说至关重要，同时对于家家户户的供电也极为重要[1]，智能电能表的准确可靠性评估主要依靠对可靠性数据的有效利用。目前，可靠性数据主要来自加速退化试验数据和现场测试数据。

文献[2]中采用比率模型构建加速退化试验数据和现场数据之间的关系，但是该方法很难描述野外环境中的应力和应力变量。因此，文献[3]将校正因子引入寿命模型，以根据ADT和现场数据做出更准确的预测，校正因子整体上会修改模型参数和预测结果，而无需考虑每个应力的影响。

文献[4]以Gibbs抽样的马尔可夫链为基础，对随机截尾的恒加寿命试验中与之相关参数后验分布的马尔可夫链采用蒙特卡罗方法进行模拟，随机截尾条件下模型参数的贝叶斯估计由此诞生。文献[5]在定数截尾场合下,建立威布尔寿命型产品的步进应力加速寿命试验模型，其中，采用牛顿拉普森法求解似然方程，其极大似然估计也随之求出，模型采用随机模拟方法验证其准确性和可实施性。

现有的异构多源数据融合方法主要考虑了基于加速退化试验数据[6-9]、实验室加速寿命试验数据[10-11]、现场条件下的寿命数据[12-16]和伯努利数据的信息融合[17]等。

文献[6]将加速降解试验得到的降解数据作为现场剩余寿命预测的先验信息，外推正常条件下的降解模型，结合现场样品的降解数据模型，建立了状态转移模型，并假设退化状态为时变退化状态，以预测现场条件下的使用寿命。文献[7]针对产品性能退化轨道的描述采用Wiener过程来解释,此过程中若产品性能接近到某一阈强度时,应改变其应力水平，同时应通过特定办法来求解其模型参数的极大似然估计—贝叶斯马尔科夫链蒙特卡罗办法，并利用仿真实验来考证文中的方法及其模型。文献[8]针对某种产品进行了各种应力类型的加速退化试验，并将这些加速退化试验获得的数据进行了关联和加权，通过互斥理论评估了锂电池的可靠性。文献[9]对于加速退化的实验信息研究分析，应通过以广义多应力加速模型为基准，确定智能电能表的寿命分布规律,起步研究分析了威布尔分布模型参数和环境应力之间存在的关系,产生了新的以数线性回归模型为基础的多应力退化模型；接着对正常应力水平下寿命分布模型的参数以新的校正办法取得解释,以期取得了正常应力水平下其有效及其残余寿命的预料成果。文献[10]综合实验室降解试验数据和现场条件监测信息，通过耦合建模策略，将随机效应动态协变量和标记过程逐步融入到基线随机退化模型中，引入随机效应处理样本间的差异。然后，利用动态协变量来处理外部条件的变化，而以贝叶斯办法来实现参数预测和退化分析，利于信息集成和可靠性评估。文献[11]把一般威布尔分布转变为指数分布,需要以寿命服从指数分布为准,同时提供恒加应力加速寿命实验中产品有关失效率的贝叶斯估计和威布尔发布的相关产品基于寿命实验的没有效用时间的预估对策，最后，完成了相应的数值模拟。文献[12]依据相关的标准和办法对加速寿命实验方案进行优化研究设计，同时以守恒不变的应力加速寿命实验信息为基础，其目标则为正常工作时应力水平寿命预估值的产品方差最小值，并且其设计变量为各实验应力转换时间和水平，从而建构步进应力加速寿命实验信息优化设计研究的数学模型，而该模型则是利用了Nelson累积失效模型和极大似然估计理论。文献[13]建立了以贝叶斯方法为基论的智能电能表稳定性评估办法，结合伪寿命数据的数据处理办法和计算模型以及智能电能表的整表失效数据。文献[16]使用多个产品具有相似设计的特定场景来预测现场回收率，由于每个产品都有离散的实验室数据和连续的现场数据，因此构建了分层模型，将实验室和从类似产品收集的现场数据之间的故障信息集成起来。文献[17]提出了三种贝叶斯推理模型，建立了退化数据、寿命数据和合格/失效伯努利型数据之间的关系，并通过集成解决了相关问题，提高了可靠性预测的精度。然而，这种方法主要处理来自多个数据源的数据，而不管这些数据是来自测试数据还是现场操作数据。

然而，现有的研究还没有进一步探讨加速退化试验数据和状态数据的数据融合方法，而这种情况在实际应用中也经常出现，因此，该融合方法具有重要研究意义。

为此，文中提出了一种新的数据融合方法，该方法对退化量服从正态分布的加速退化试验数据和现场采集的多状态数据进行融合，同时，综合研究了工作条件和环境应力对产品性能和可靠性的影响。根据实际环境应力信息、工况信息、现场使用条件下检测到的信息以及加速多源信息(如加速退化测试数据)，建立了一种更接近实际变化的电子产品可靠性评估模型。

1 数据融合方法的框架

文中认为智能电能表运行状态的概率评估主要基于两种数据：加速退化试验的退化数据和现场检测的状态数据。数据融合方法首先对加速退化试验的退化数据进行处理，建立描述退化数据轨迹的退化模型，然后将加速条件下得到的数据外推到正常使用条件下所需的加速方程,采用最大似然估计法求解加速模型和退化模型的参数。然后,将基于加速退化试验数据估计的模型参数作为先验信息，将加速退化试验数据与现场检测到的状态数据相融合，建立联合似然函数，并用贝叶斯方法估计模型参数的后验估计结果。

所提出的“数据融合”是采用最大似然估计法对加速退化试验数据进行参数预测，并将参数估计结果作为现场检测状态数据融合模型参数的先验信息，实现了加速退化试验数据与现场检测状态数据的融合。

智能电能表数据融合方案具体实现流程如图1所示。

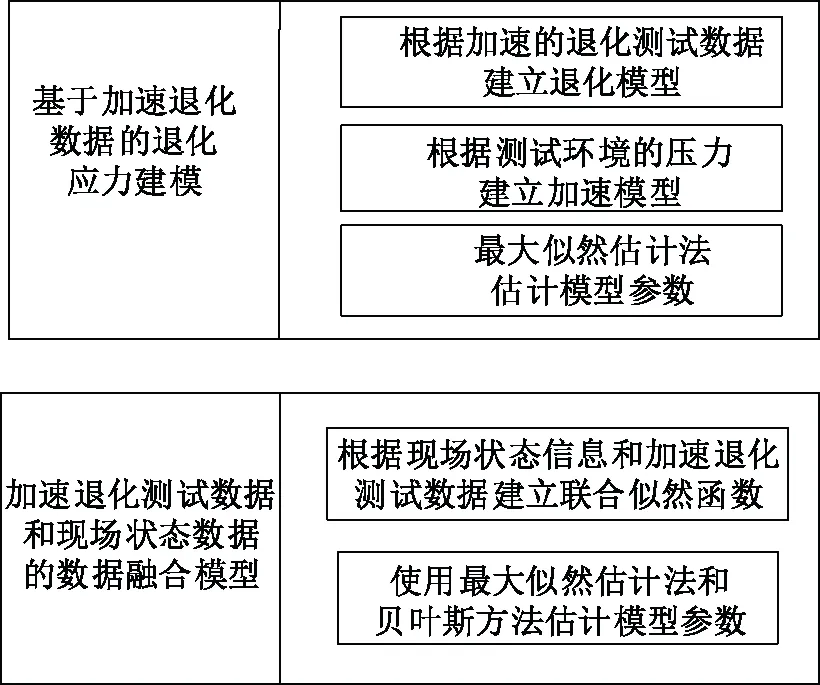
图1 智能电能表的数据融合流程图Fig.1 Data fusion flow chart of smart electricity meter

2 基于加速退化试验数据的退化应力建模

文中主要以智能电能表的恒应力加速退化试验为基础，建立退化模型，用以描述不同应力下退化数据的轨迹趋势。同时，利用加速度应力外推到正常使用条件下的数据建立加速度模型，以获得正常条件下的退化轨迹模型。智能电能表测量精度的表征参数是测量误差，因此本文所指的退化数据是测量误差数据，退化量的增量基于测量增量数据，退化数据来自多应力加速退化试验。

2.1 退化模型

基于智能电能表的基本误差数据，建立了线性wiener过程退化模型，具体如下：

Y(t)=νt+σB(t)+y0

(1)

式中ν表示漂移参数并反映降解率；σ是挥发性参数；B(t)是标准布朗运动；y0是初始降解值。

2.2 加速模型

根据已有的研究，温度和湿度是影响智能电表环境压力的两个重要因素。因此，本文在恒定应力加速退化试验的基础上，建立了温度和湿度的综合加速模型，其中t代表绝对温度(单位:K)，RH代表相对湿度(单位:%)：

(2)

2.3 基于加速退化试验数据的模型参数估计

在加速退化试验中，漂移参数具有特殊的物理意义，在加速应力水平下，加速退化率为：

(3)

式中Ti为绝对温度(K)；RHi为相对湿度(%)。

由式(1)可知：应力为i时，样品j在时间点k的退化量增量Δijk为正态分布，即满足：

Δyijk～N(νiΔtijk,σ2Δtijk)

(4)

利用最大似然估计法以守恒不变的应力加速退化实验为基础，对退化模型的参数进行预测，第i个应力、第j个样品在第k个时间点的数据的似然函数可以表示为：

(5)

取上述似然函数的对数，并取其对参数集{β0,β1,β2,σ}的偏导数，有：

(6)

2.4 正常运行条件下的可靠性评估

假设T0和RH0分别为仪表正常使用条件下的温度和湿度，式(3)表明正常使用条件下的退化率为：

(7)

设产品性能参数的故障阈值为Df，则其可靠性表达式可写为：

(8)

3 基于ADT数据和现场状态数据的数据融合模型

3.1 状态概率模型的建立

本节考虑融合两种类型的数据：现场多状态数据和加速退化试验降级数据。

多状态数据表示产品的抽样检验状态记录，可分为优、良、中、差四种状态，分别定义为：

(1)优：现场测试值在故障阈值的[0,30%]范围内；

(2)良：现场测试值在故障阈值的[30%，60%]范围内；

(3)中：现场测试值在故障阈值的[60%，100%]范围内；

(4)差：现场测试值超过故障阈值的100%。

式(8)中，假定产品的平均工作时间为t0，现场产品采样的四种状态(优、良、中、差)的存在概率如下：

所选产品状态处于优良状态的概率为：

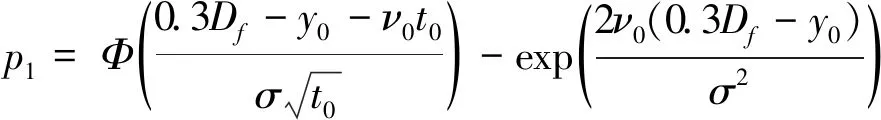
(9)

所选产品处于良好状态的概率为：

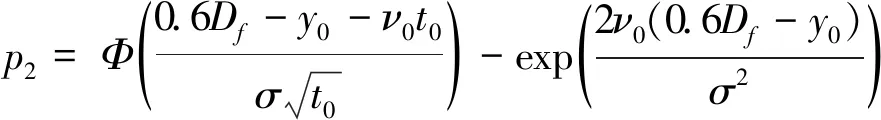
(10)

所选产品处于中状态的概率为：

(11)

那么，产品处于不良状态的概率则可以表示为：

1-p1-p2-p3

(12)

3.2 贝叶斯参数估计

本小节采用贝叶斯理论进行参数后验估计。贝叶斯学派的基本思想是：未知数θ不论为何数都可以变成一个随机变量，同时利用概率分布来说明θ的未知情况。该概率分布体现了关于θ采样前的一些先验信息，也可称为先验分布。因此，我们把以一般信息、样本和先验信息为基础的统计推断合称为贝叶斯统计。

贝叶斯统计所促进的信息融合是把样本信息结合先验信息，然后用先验信息拓展样本信息，并通过更新和修正得到对问题的最终理解，从而完成信息融合。

下列表达式是依据贝叶斯原理，将似然函数乘以先验发布(乘常数)得到后验分布，可写成：

后验分布∞似然函数×先验分布

(13)

由贝叶斯理论和式(13)知道前验分布乘以其似然函数会得到其后验分布，表示为：

π(Θ0|Y)∞L(Y|Θ0)π0(Θ0)

(14)

上述退化模型和加速模型中，需要求解其参数集{β0,β1,β2,σ}，然后采用加速退化试验数据估计参数作为参数的先验信息，将现场检测到的状态数据和加速退化试验成果进行结合，得到模型参数的后验预测结果。融合数据的似然函数表达式如下：

(15)

式中M1、M2、M3、M4分别表示与现场数据中的优、良、中、差四个状态相对应的样本量。

后验参数估计采用贝叶斯法，参数集的后验分布可表示为：

π(σ,βi|Δy,Δt,Df,y0,t0,M1,M2,M3,M4)∞Lπ(σ)×

(16)

这里，假设参数Θ0={β0,β1,β2,σ}的先验分布是正态分布：

(17)

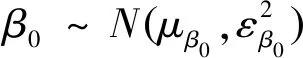
β0条件后验分布：

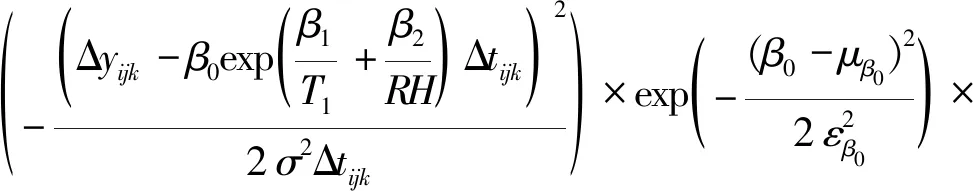
(18)

β1条件后验分布：

(19)

β2条件后验分布：

(20)

σ条件后验分布：

(21)

由于很难以解析形式获得模型参数的后验分布，因此常用方法是通过马尔可夫链蒙特卡罗法模拟采样获得后验参数。马尔可夫链蒙特卡罗法主要包括两种采样算法：Gibbs采样算法和Metropolis-Hastings算法。文中采用后者。Metropolis-Hastings算法的实现过程如图2所示。

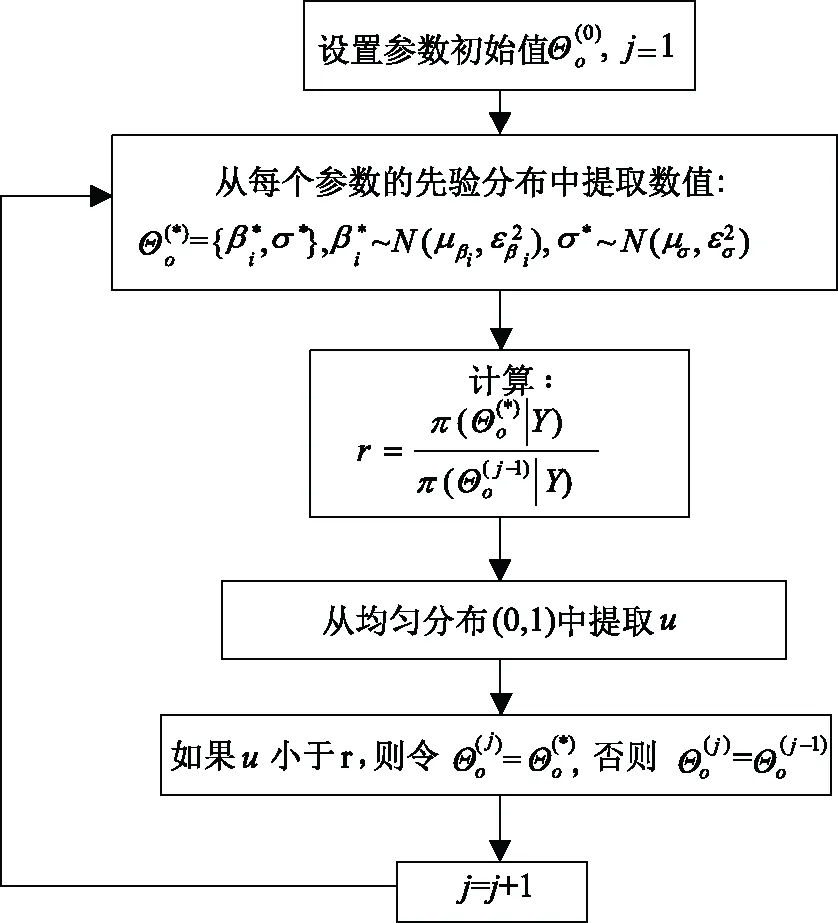
图2 metropolis-hastings抽样算法参数估计的后验结果流程图Fig.2 Posteriori results flow chart of parameter estimation by metropolis-hastings sampling algorithm

4 算例

本文算例中，将智能电能表的计量误差视为性能退化参数，表示为参考表的计量脉冲与电能表某一负荷点被测表的计量脉冲的差额，继而与参考表的计量脉冲对比，即：

湿度、温度综合加速退化实验应力水平组合见表1，利用现场获得的同批次智能电能表随机抽样选取出9个(其中一个为参考表计)，进行恒定应力加速退化试验，所获得的加速退化数据如图3所示。

表1 加速退化试验应力组合Tab.1 Stress combination of the accelerated degradation test

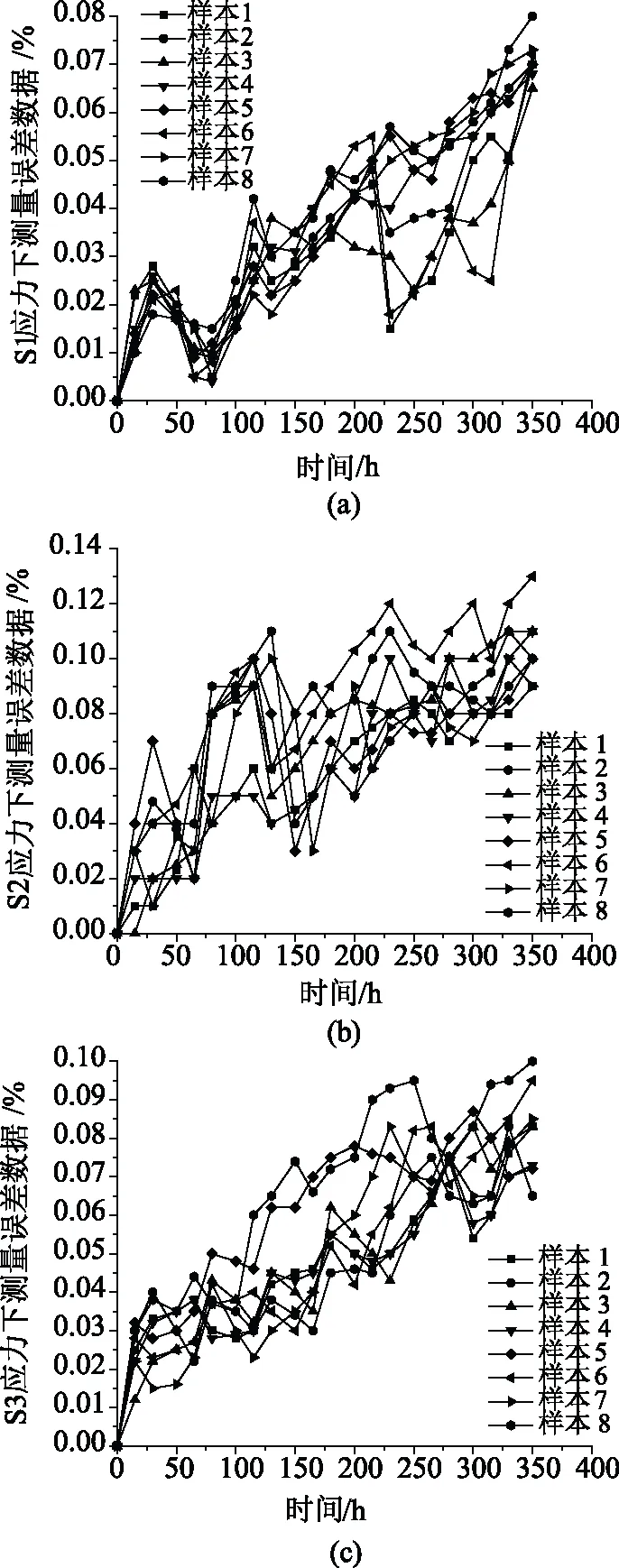
图3 不同应力下加速退化试验的测量误差数据%Fig.3 Measurement error data under various stresses of ADT (%)

将图3获得的不同应力下加速退化试验的测量误差数据作为先验信息，由式(6)，采用最大似然法获得参数集的估计结果，如表2所示。

表2 基于加速退化试验数据的参数极大似然估计Tab.2 Parametric maximum likelihood estimation based on accelerated degradation test data

利用获得的一批现场状态数据，首先计算智能电能表的平均工作时间t0，得到t0=20 000 h。此时各状态样本量统计数量如表3所示。

表3 平均工作时间内各产品状态测试结果Tab.3 Status test results of each product during the average working time

为求解各参数的后验分布，本文基于Matlab，采用马尔可夫链蒙特卡罗法实现了Metropolis-hastings算法。计算得到的参数{β0,β1,β2,σ}结果图4～图7所示。

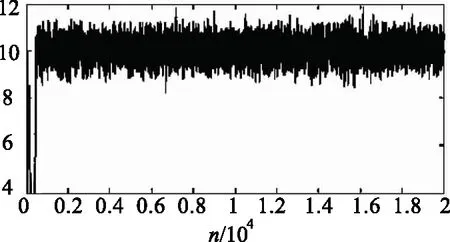
图4 β0后验估计Fig.4 Posterior estimation of β0

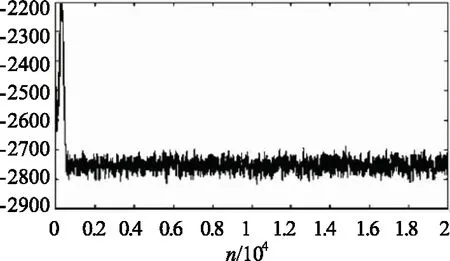
图5 β1后验估计Fig.5 Posterior estimation of β1

图6 β2后验估计Fig.6 Posterior estimation of β2

图7 σ后验估计Fig.7 Posterior estimation of σ

表4是根据上述计算结果，n=10 000次迭代后马尔可夫链蒙特卡罗法算法的参数平均值，即融合后的参数结果(加速退化试验数据和现场状态数据融合)，与融合前的参数结果(仅有加速退化试验数据)的对比结果。

表4 数据融合前后参数的比较Tab.4 Comparison of parameters before and after data fusion

将上述模型参数代入式(8)，最终融合信息前后的可靠性评估结果如下：

由图8可知，信息融合前(仅使用加速退化试验数据)得到的稳定性结果变化较快，而信息融合后(结合加速退化试验数据和现场状态数据)得到的稳定性结果变化较慢，即修改后得到的评估结果是根据现场状态信息建立的模型参数。通过对图8结果的比较，可以得出在实际使用条件下状态对电能表的可靠性评估结果有很大影响的结论。

图8 仅比较融合状态数据和加速退化试验数据的评估结果Fig.8 Comparison of evaluation results between fusion state data and ADT data only

将现场检测得到的四种状态数据(优、良、中、差)与实验室退化数据进行融合后，利用式(9)～式(12)得到四种状态概率随时间的变化，如图9所示.

图9 四种状态概率曲线变化曲线图Fig.9 Probability curve of four states over time

图9给出了智能电能表“优、良、中、差”四种状态的概率随时间变化曲线。图中，智能电能表状态为“优”的概率曲线p1随时间逐渐减小，这与电能表批次状态随时间减小的实际情况一致。状态为“良”的智能电能表的概率曲线p2随时间先呈上升趋势，后呈下降趋势，说明在上升阶段，部分状态为“良”的智能电能表会变为“良”状态，使初期的p2曲线呈上升趋势，下半年的下降趋势是由于智能电能表在良好状态下转为中等状态，与实际情况相符。p3为智能电能表在“中”状态下的概率曲线，先是呈上升趋势，然后随时间呈下降趋势。其上升阶段的时间明显长于“良”状态下的曲线，说明智能电能表在“良”状态下变为“中”状态。曲线p4代表的是“差”状态的概率，由于初期电能表批次中没有“差”状态的智能电能表，所以其趋势一直不变，是上升的。可是，随着时间的延伸，智能电能表在各个状态下的性能开始下降，最终出现“差”状态的概率增大，这是符合实际的。上图还显示了给定时间点电能表四种状态的概率。