函数重排类的刻画及其在定常涡块构造中的应用*
2022-02-17江毅
江 毅
(福州理工学院计算与信息科学学院数学系,福建 福州 350506)
函数重排理论作为分析与几何的一个重要结合,是极其有用的工具.众所周知,许多不等式往往是在具有最优对称性的情形下达到最优的,如等周不等式表明,在体积一定的条件下,球具有最小的表面积.在函数重排理论中,核心主题就是对某种最优对称状态的刻画.学者对重排理论进行了深入研究,提出了许多重排定理,如Riesz重排不等式[1]、Brascamp-Lieb-Luttinger不等式[2]和Brunn-Minkowski不等式[2]等.根据这些函数重排理论同样可以推导出等周不等式[3],也可以推导出Sobolev不等式[4]和Hardy-Littlewood-Sobolev不等式[1]的最优解是球对称函数等结论.
对于一个给定的函数,如何刻画它自身所有重排函数所构成的函数类及其在适当拓扑下的闭包,是一类基本的问题,这在具体问题的应用中也非常重要.笔者拟构造一类特征函数,通过在测度区间上构造函数的方法给出其重排类弱闭包的另一个等价刻画,并且将该结果应用于定常涡块的构造问题中.
1 预备知识
设(Ω,μ)和(Ω′,μ′)是正测度空间,且μ(Ω)=μ′(Ω′)<+∞.考虑可测函数f:Ω→R,g:Ω′→R,称f和g互为重排函数,如果对于∀t∈R,有μ(f-1[t,+∞))=μ′(g-1[t,+∞)).由文献[1]可知,f存在一个单调不增的函数fΔ:(0,μ(Ω))→R,使得f和fΔ互为重排函数.需要指出的是,这里开区间(0,μ(Ω))赋予的是一维Lebesgue测度.
给定映射ρ:Ω→Ω′,称映射ρ是从Ω到Ω′的保测变换,如果对于每个μ′-可测子集A⊂Ω′,其原象集ρ-1(A)都是μ-可测的,且μ(ρ-1(A))=μ′(A).进一步,称映射ρ是从Ω到Ω′的保测双射,如果ρ具有逆映射,且也是保测变换.称(Ω,μ)是一个测度区间[5],如果存在一个从测度空间(Ω,μ)到区间(0,μ(Ω))的保测双射.


引理1给出了函数重排类弱闭包的一个刻画.这个刻画具有普遍性,但结果是抽象的,因此在具体问题的应用中需要一些更具体的描述.为了简单起见,这里主要考虑特征函数的情形,即某个集合的示性函数.对于给定的集合A,将A上的特征函数记为1A.本研究的主要目标就是给出特征函数的重排类弱闭包的另一个等价刻画.
2 主要结果及其证明
定理1设(Ω,μ)是一个测度区间,1≤p<+∞,A⊂Ω,f0=1A.将f0在Ω上的所有重排函数全体构成的函数类记为F,则有
证明记
根据引理1,只需证明A1=A2.
首先证明A2⊆A1.任取f∈A2,要证明f∈A1,只需证明
(1)
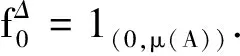
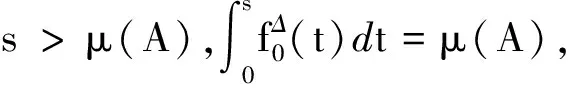
(2)
由(2)式可得(1)式,从而A2⊆A1.
接下来证明A1⊆A2.对于任取的f∈A1,即要证明f∈A2.
采用反证法.先假设{x∈Ω|f(x)>1}为正测集,那么存在s0∈(0,μ(Ω)),使得fΔ(s0)>1.由fΔ的单调性可知,在(0,s0]上都有fΔ(s)>1,由此可得
该结果与f∈A1的事实矛盾,因此在Ω上f几乎处处小于或等于1.
再假设{x∈Ω|f(x)<0}为正测集,那么存在s0∈(0,μ(Ω)),使得fΔ(s0)<0.由fΔ的单调性可知,在[s0,μ(Ω))上都有fΔ(s)<0,由此可得
该结果也与f∈A1的事实矛盾,因此在Ω上f几乎处处大于或等于0.
综上可得f∈A2.证毕.
3 重排类在定常涡块构造中的应用
Turkington[7]将定常涡块的构造问题归结为一个变分问题.设D⊆R2为一个有界单连通的光滑区域,-Δ在D中带有零边值的格林函数记为g(x,x′),定义
其中:D赋予的是二维Lebesgue测度,其测度记为m(D);λ表示涡强参数,λ>(m(D))-1.
Turkington考虑了如下极大化问题:
他证明了能量泛函E在Kλ(D)上的极大元可以达到,且这个极大元具有涡块形式(见文献[7]中的Theorem 2.1和Corollary 2.3).Turkington的证明虽极具技巧性,但稍显冗长.在这里,可以利用定理1,将这个极大化证明吸纳到抽象的泛函框架中,给出更简洁的证明.
事实上,由定理1可知,Turkington所定义的Kλ(D)实际上就是D中高度为λ、总质量为1的所有特征函数的弱闭包.于是利用Burton[6]建立的理论(Lemma 2.15)能推导出能量泛函E在Kλ(D)上的极大元不仅可以达到,而且具有涡块形式,这样就完成了文献[7]中Theorem 2.1和Corollary 2.3的证明.
